文档内容
重庆市万州第三中学等多校联考2024-2025学年高一下学期4月期中考试
数学试题
一、单选题
1.已知向量 满足 ,则 ( )
A. B.1 C. D.2
2.复数 的实部与虚部之和为( )
A. B. C. D.
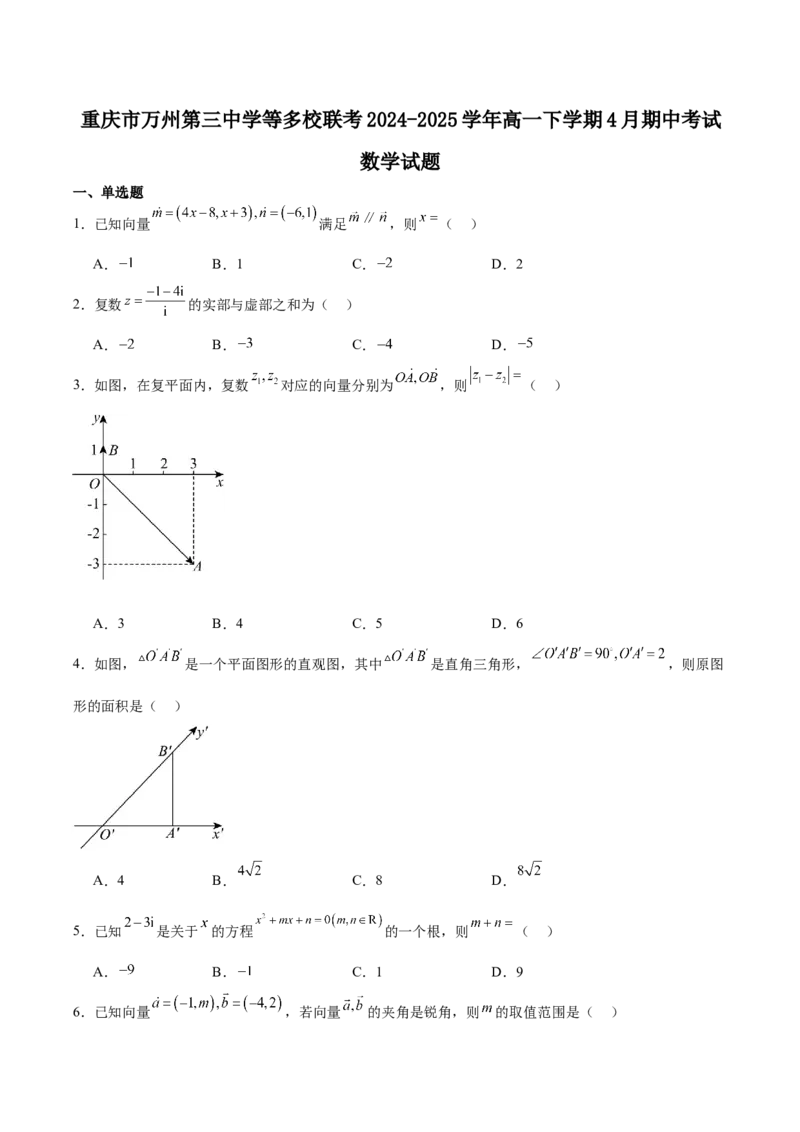
3.如图,在复平面内,复数 对应的向量分别为 ,则 ( )
A.3 B.4 C.5 D.6
4.如图, 是一个平面图形的直观图,其中 是直角三角形, ,则原图
形的面积是( )
A.4 B. C.8 D.
5.已知 是关于 的方程 的一个根,则 ( )
A. B. C.1 D.9
6.已知向量 ,若向量 的夹角是锐角,则 的取值范围是( )A. B.
C. D.
7.记 的内角 的对边分别为 ,已知 为锐角,且 ,则
的周长为( )
A. B. C. D.
8.设正四棱台 上、下底面的边长分别为 ,高为 ,若 ,
则正四棱台 的体积为( )
A. B. C.140 D.142
二、多选题
9.下列结论正确的是( )
A.若 的内角 满足 ,则 一定是钝角三角形
B.绕直角三角形一条边所在直线旋转一周所形成的几何体是圆锥
C.若 是纯虚数,则
D.若向量 ,则向量 在向量 上的投影向量是
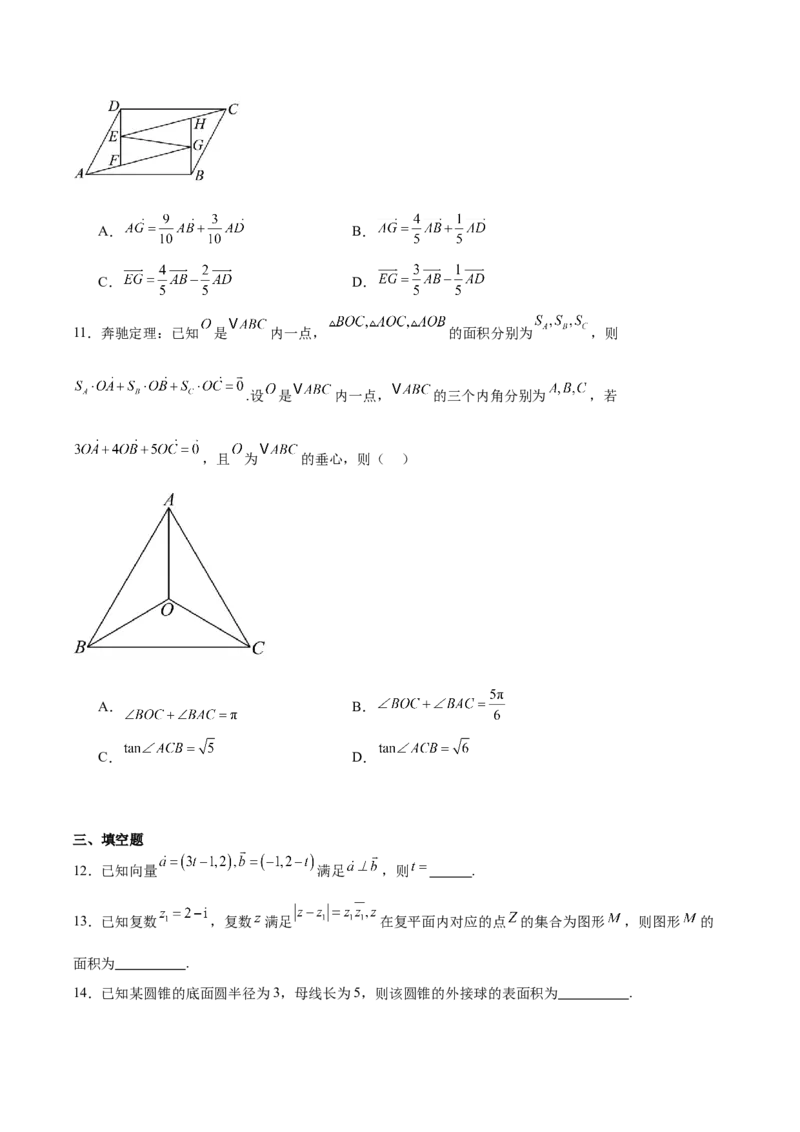
10.“赵爽弦图”是中国古代数学的经典成果,它是由四个全等的直角三角形与一个小正方形拼成的一个
大正方形.如图,某人仿照“赵爽弦图”,用四个三角形和一个小的平行四边形拼成一个大平行四边形,其
中 分别是线段 上靠近 的三等分点,则( )A. B.
C. D.
11.奔驰定理:已知 是 内一点, 的面积分别为 ,则
.设 是 内一点, 的三个内角分别为 ,若
,且 为 的垂心,则( )
A. B.
C. D.
三、填空题
12.已知向量 满足 ,则 .
13.已知复数 ,复数 满足 在复平面内对应的点 的集合为图形 ,则图形 的
面积为 .
14.已知某圆锥的底面圆半径为3,母线长为5,则该圆锥的外接球的表面积为 .四、解答题
15.已知复数 .
(1)若 是实数,求 的值;
(2)若 在复平面内对应的点位于第二象限,求 的取值范围;
(3)若 ,求 的值.
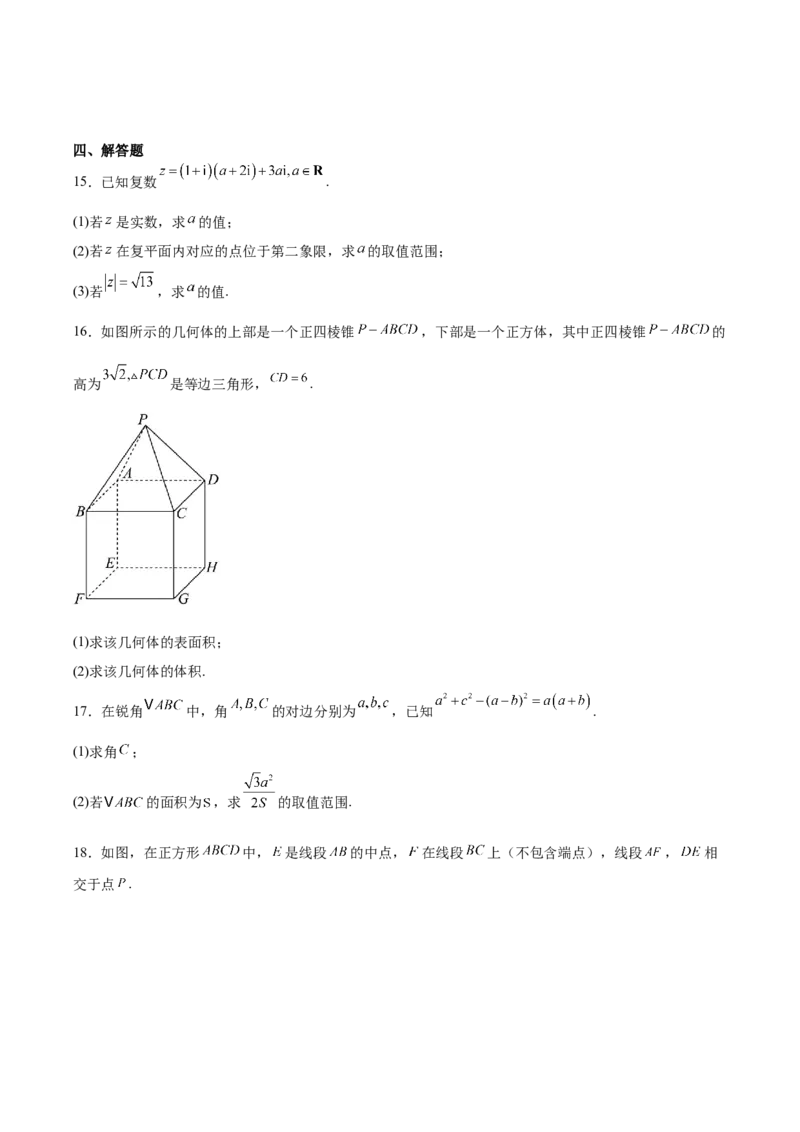
16.如图所示的几何体的上部是一个正四棱锥 ,下部是一个正方体,其中正四棱锥 的
高为 是等边三角形, .
(1)求该几何体的表面积;
(2)求该几何体的体积.
17.在锐角 中,角 的对边分别为 ,已知 .
(1)求角 ;
(2)若 的面积为 ,求 的取值范围.
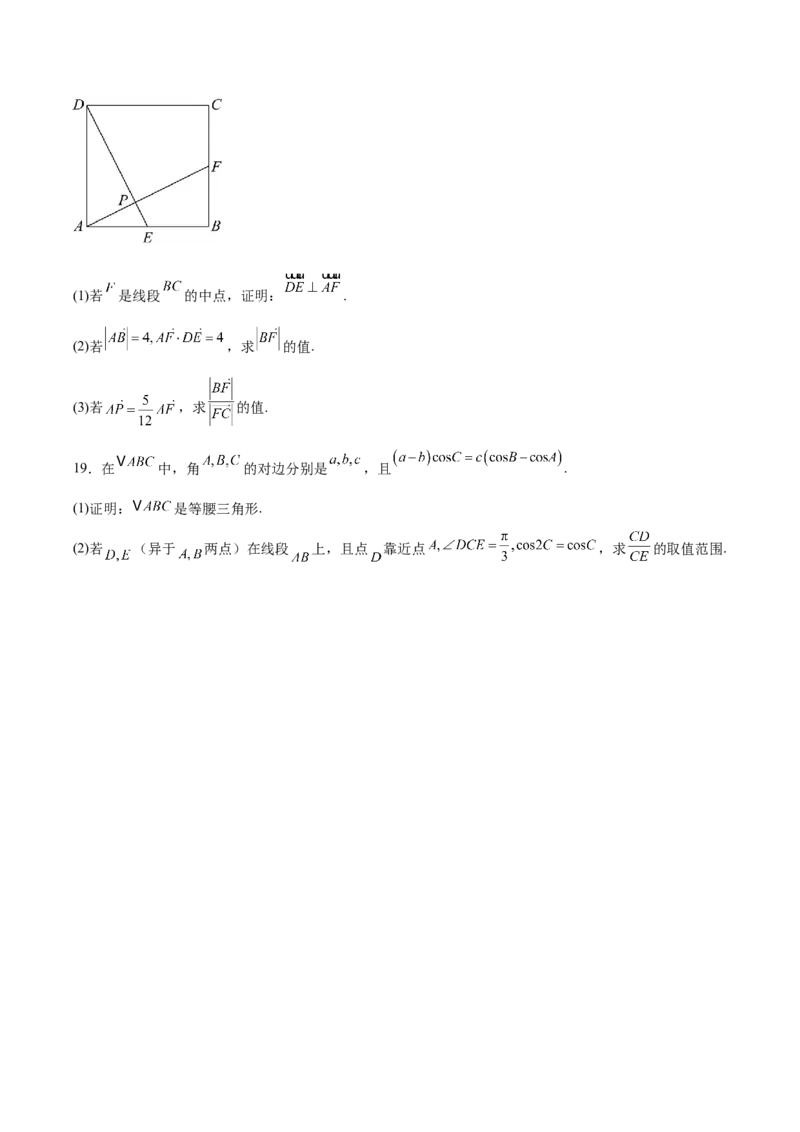
18.如图,在正方形 中, 是线段 的中点, 在线段 上(不包含端点),线段 , 相
交于点 .(1)若 是线段 的中点,证明: .
(2)若 ,求 的值.
(3)若 ,求 的值.
19.在 中,角 的对边分别是 ,且 .
(1)证明: 是等腰三角形.
(2)若 (异于 两点)在线段 上,且点 靠近点 ,求 的取值范围.题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B D C B A ACD AC
题号 11
答案 AC
1.A
根据共线向量坐标运算列式求解即可.
【详解】因为向量 满足 ,所以 ,解得 .
故选:A
2.B
先利用复数的除法运算化简,再根据实部和虚部的定义即可求出.
【详解】因为 ,
则该复数的实部为 ,虚部为 ,
所以该复数的实部与虚部之和为 .
故选:B
3.C
根据复数的几何意义求解即可.
【详解】由图可得 ,所以 ,所以 .
故选:C
4.B
还原 ,求出其边长即可求解直角三角形的面积.
【详解】如图, 的直观图是 ,则 ,
则 的面积为 .故选:B
5.D
首先根据实系数一元二次方程的根的特征求另外一个根,再根据韦达定理,即可求解.
【详解】由题意可得关于 的方程 的另一个根为 ,
则 ,解得 ,则 .
故选:D
6.C
根据平面向量数量积的坐标运算求解 ,再根据向量 的夹角是锐角与数量积与向量共线的关系列式
求解即可.
【详解】因为 ,所以 ,
因为向量 , 的夹角是锐角,所以
解得 且 ,所以 的取值范围是 .
故选:C.
7.B
由正弦定理化边为角化简得 ,进而求得 ,根据余弦定理求得 ,即可求解周长.
【详解】因为 ,所以 ,
又 ,则 ,又 为锐角,所以 .
由 ,得 ,解得 ,
则 的周长为 .
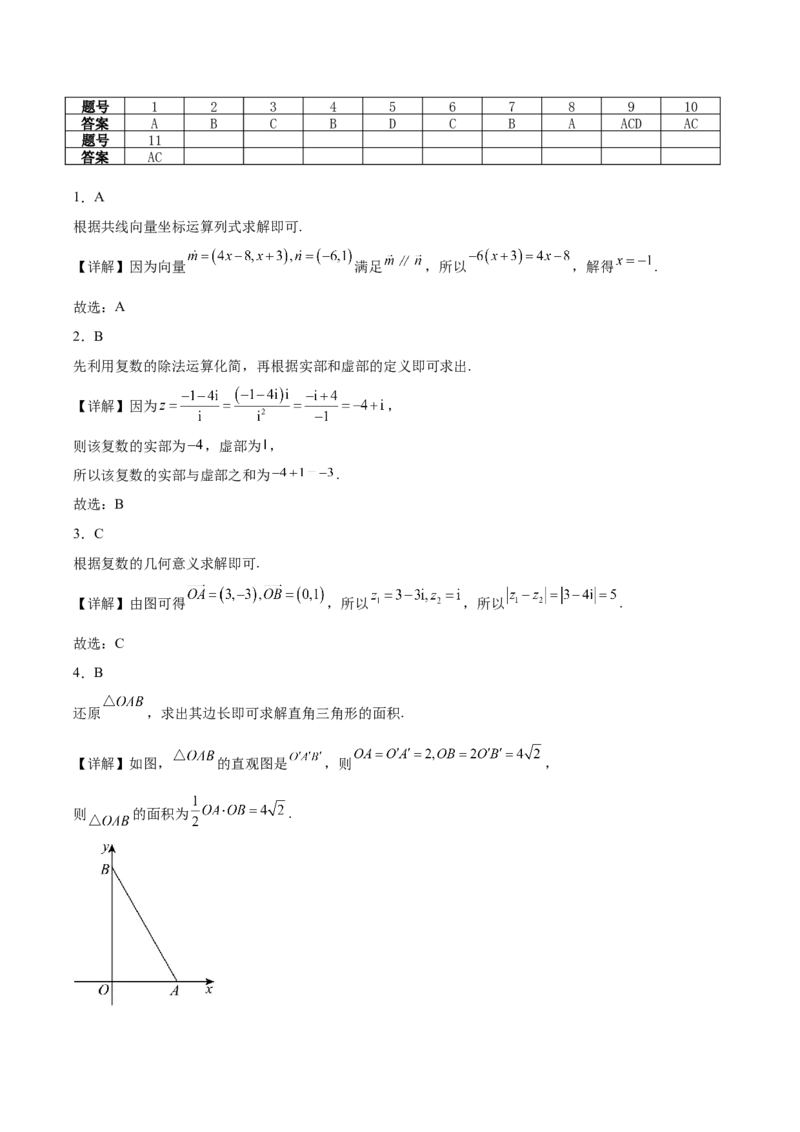
故选:B8.A
A B C D
设正方形 1 1 1 1的中心为 ,正方形 的中心为 ,再根据几何关系求解 ,进而可得
,结合正四棱台的体积公式求解即可.
A B C D
【详解】设正方形 1 1 1 1的中心为 ,正方形 的中心为 ,在直角梯形 中,
,
由 ,得 ,解得 (负值已舍去),
从而 ,
所以正四棱台 的体积 .
故选:A
9.ACD
利用正弦定理角化边,再用余弦定理判断A;利用圆锥的定义判断B;利用纯虚数的定义判断C;求出投
影向量判断D.
【详解】对于A,设 的内角 所对的边分别为 ,由 ,
得 ,由余弦定理得 , 是钝角, 是钝角三角形,A正确;
对于B,绕直角三角形的斜边所在直线旋转一周所形成的几何体是共底面的两个圆锥,B错误;对于C,由 是纯虚数,得 ,解得 ,C正确;
对于D,向量 在向量 上的投影向量是 , D正确.
故选:ACD
10.AC
运用向量运算加减法则,结合基本定理得解.
【详解】由题意可得 .
因为 是平行四边形,所以 ,所以 ,
所以 ,则A正确,B错误.
因为 ,
所以 ,则C正确,D错误.
故选:AC.
11.AC
根据垂心性质判断AB,结合垂心性质及数量积的定义可得 ,结合已知根
据奔驰定理得 ,根据面积公式可得 ,设
,由 及两角和的正切公式列方程求得 ,即
可得解.
【详解】因为 为 的垂心,所以 ,A正确,B错误.
由上知 ,
同理, .因为 ,所以 ,
所以 ,同理, ,
所以 .
因为 ,所以
.
设 ,
因为 ,所以 ,
所以 ,解得 ,所以 ,C正确,D错误.
故选:AC
12.1
利用向量垂直的坐标形式列式即可求解.
【详解】因为向量 满足 ,
所以 ,解得 .
故答案为:1
13.
根据复数的几何意义求解即可.
【详解】因为 ,所以 ,
则 在复平面内对应的点 的集合是以点 为圆心,5为半径的圆,图形 的面积为 .
故答案为:
14.
根据外接球的性质,求外接球的半径,再列式求解.【详解】设该圆锥的高为 ,外接球的半径为 ,则 .
由 ,解得 ,
所以该圆锥的外接球的表面积 .
故答案为:
15.(1) .
(2) .
(3) 或 .
(1)先算出 表达式,实数虚部是 ,让虚部对应式子为 求 .
(2)已知 形式,按条件列不等式组,分别解不等式,取交集得 范围.
(3)由模的值列等式,两边平方去掉根号,展开合并得方程,因式分解求解 .
【详解】(1) ,
因为 是实数,所以 ,解得 .
(2)因为 ,所以
解得 ,即 的取值范围为 .
(3)因为 ,所以 ,
化简得 ,
解得 或 .
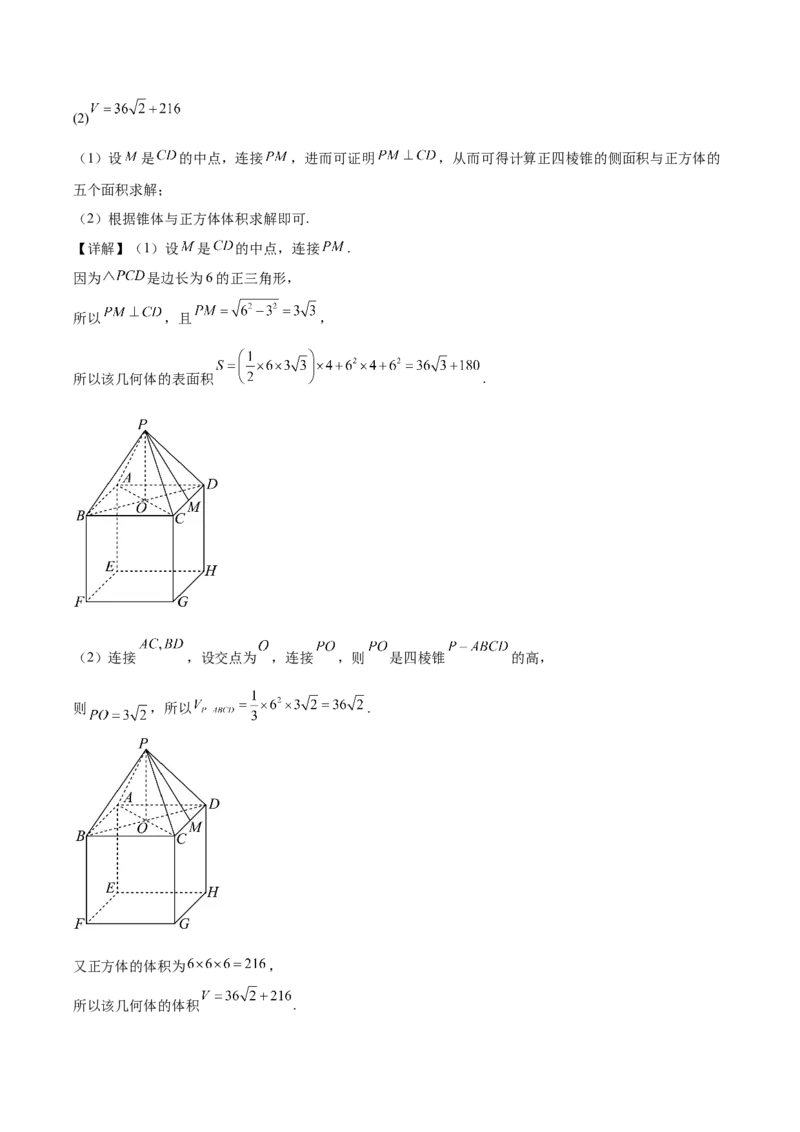
16.(1)(2)
(1)设 是 的中点,连接 ,进而可证明 ,从而可得计算正四棱锥的侧面积与正方体的
五个面积求解;
(2)根据锥体与正方体体积求解即可.
【详解】(1)设 是 的中点,连接 .
因为 是边长为6的正三角形,
所以 ,且 ,
所以该几何体的表面积 .
(2)连接 ,设交点为 ,连接 ,则 是四棱锥 的高,
则 ,所以 .
又正方体的体积为 ,
所以该几何体的体积 .17.(1) .
(2) .
(1)化简结合余弦定理求解即可
(2)根据面积与正弦定理可得 ,结合 可得 ,再根据三角关系可得
,进而可得取值范围.
【详解】(1)因为 ,
所以 ,
整理得 ,
所以 .
因为 ,所以 .
(2)因为 的面积 ,
所以 .
又 ,所以 ,则 .
又因为 所以 ,
所以 ,故 ,即 的取值范围是 .
18.(1)证明见解析
(2)1
(3) .
(1)利用基底 表示向量 和 ,再求数量积;
(2)首先设 ,再代入数量积的运算,即可求解;
(3)利用基底 表示向量 ,再根据三点共线,即可求解.
【详解】(1)证明:因为 分别是线段 的中点,所以 ,
则 ,
所以
由正方形的性质可知 ,则
即 ,故 .
(2)设 ,则 .
由(1)可知 ,则 .
因为 ,所以 ,
解得 ,则 .
(3)设 ,则 .因为 ,所以 .
因为 是线段 的中点,所以 ,所以 .
因为 三点共线,所以 ,解得 ,
则 ,故 .
19.(1)证明见解析
(2) .
【详解】(1)证明:因为 ,
所以 ,
所以 ,
所以 .
因为 ,所以 ,
所以 ,所以 ,即 是等腰三角形.
(2)因为 ,所以 ,即 ,
解得 舍去 .
因为 ,所以 .
由(1)可知 ,所以 .
设 ,则 .
在 中,由正弦定理可得 ,则 .
在 中,由正弦定理可得 ,
则 .
因为 ,所以 .
因为 ,所以 ,所以 ,
所以 ,即 的取值范围为 .