文档内容
哈师大附中2024-2025学年度上学期高一10月阶段性考试数学答案
1. .B
因为 , ,
所以 .
故选:B.
2. D
,
故选:D
3. B
对于①:因为0是 的元素,所以 ,故①正确;
对于②:因为空集是任何集合的子集,所以 ,故②正确;
对于③:因为集合 的元素为0,1,集合 的元素为(0,1),
两个集合的元素全不相同,所以 之间不存在包含关系,故③错误;
对于④:因为集合 的元素为 ,集合 的元素为 ,
两个集合的元素不一定相同,所以 不一定相等,故④错误;
综上所述:正确的个数为2.
故选:B.
4. B
当 时,该方程为 ,是一元一次方程,此时方程有一个实数根 ;
当 时,方程 为一元二次方程,
因为方程 有实数根,
所以 ,解得 且 ,
综上, 的取值范围是 ,
故选:B.5. A
对于A,A是特称命题,其否定为: , ,即 为真命题,A正
确;
对于B,∵B是全称命题,其否定为特称命题,故B排除;
对于C, C是特称命题,其否定为: , ,即 为假命题,
C错误;
对于D, D是特称命题,其否定为:任意实数x,都有 , 代入不成立,为假命
题,D错误;
故选:A.
6. C
选项A中,若 满足 ,但仍然有 ,A错;
选项B中,若 ,则 ,B错;
选项C中,则 得 , ,∴ ,C正确;
选项D中,若 ,则 ,甚至 中有一个为0时, 或 无意义,D错.
故选:C.
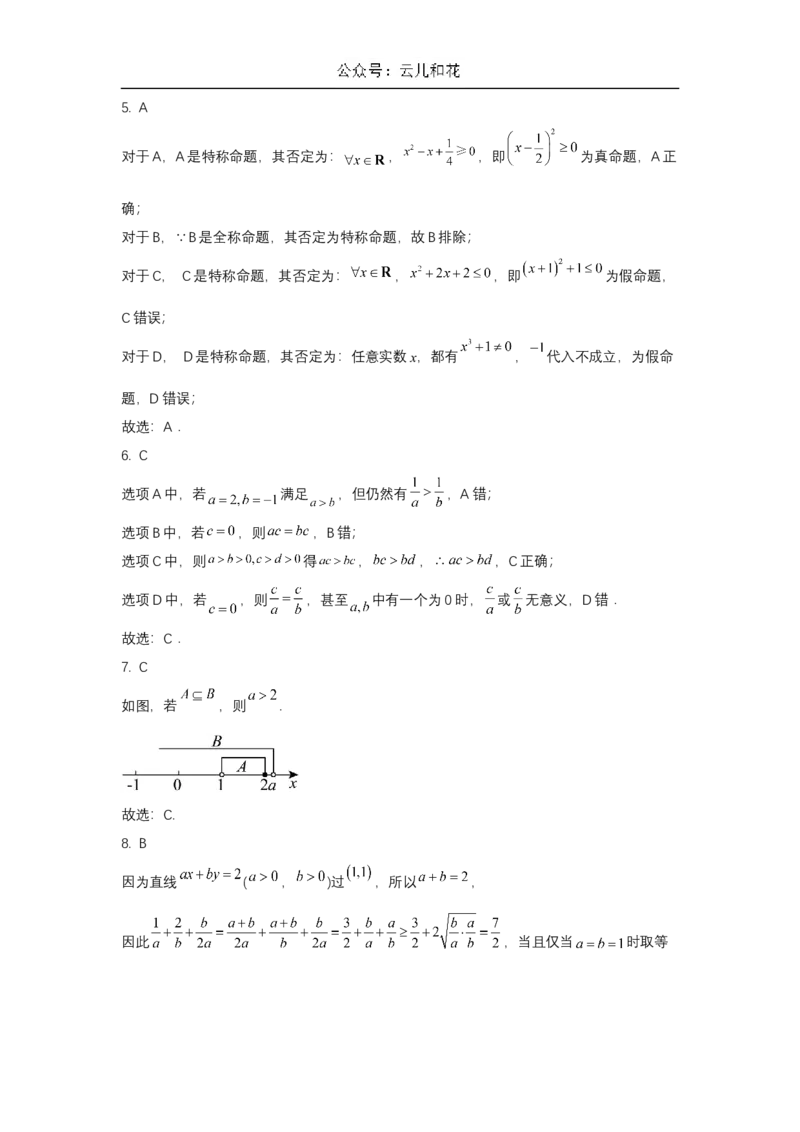
7. C
如图,若 ,则 .
故选:C.
8. B
因为直线 ( , )过 ,所以 ,
因此 ,当且仅当 时取等号,所以 的最小值为 ,
故选B
9. AC
由图可知阴影部分所表示的集合为 ,C正确,B,D错误,
因为 , ,
所以 ,故A正确.
故选:AC
10. BC
对于A,命题“ ,使 ”的否定形式是 ,使 ,故A错误
对于B,当 时, 成立,当 时,解得 或 ,故“
”是“ ” 的充分不必要条件,故B正确
对于C,若 是 的充分条件, 是 的充要条件,则有 ,故 是 的必要条件,
故C正确
对于D,若命题“ ”是假命题,则 是真命题,故
m=0或 解得 ,故D错误
故选:BC
11. BCD
因为不等式 的解集为 ,
所以 ,解得 .
所以 .即 .
故选:BCD.
12. AB
对于A:因为正数 , 满足 ,
所以 ,
当且仅当 ,即 时取等号,故A正确;
对于B: ,
所以 ,当且仅当 时等号成立,故B正确;
对于C:因为 ,即 ,且 ,
,
由抛物线的性质可得,当 时,最小值为 ,故C错误;
对于D:由C可得 ,
当 时,最大值为 ,故D错误;
故选:AB.
13.
① 时, ,原不等式可化为 ,解集为R成立;
② 时,
解得 ,
综上, ,即实数k的取值范围为 .
故答案为: .14. 7
因为 ,
,
所以满足 的集合 中必有元素2,3,
所以求满足 的集合 的个数,即求 集合的真子集个数,
所以满足 的集合 的个数为 个.
故答案为:7.
15. 4
, ,
因为 , ,所以 , ,
由 得 ,即 ,解得 或 ,
当 时,解 得 ,此时 ,不满足题意;
当 时,解 得 ,满足题意.
所以 .
故答案为:4
16.
17. ; ;
因为全集 ,集合 , ,
则 , ,
所以 ; ; .
18. (1)6(2)
1)由韦达定理得 ,
故 ;
(2) ,
故 .
19. (1)
(2)
(1)由 ,故 ,
当 时,有 ,解得 ;
当 时,有 ,解得 ;
综上所述, ;
(2)由 ,故 ,
故有 ,解得 ,
故 .
20.
由题意得,命题 ,命题 ,
是 的必要不充分条件,
是 的充分不必要条件,
即 ,且 ,
,
故实数a的取值范围为 .
21. [1,+∞).
解:若A= ,则Δ=4-4a<0,解得 a>1;
若1∈A∅,由1-2+a=0得a=1,此时A={1},符合题意;
若2∈A,由4-4+a=0得a=0,此时A={0,2},不符合题意.
综上,实数a的取值范围是[1,+∞).
22. 当 时,解集 ,当 时,解集 ,当 时,解集
或 .
【分析】对a分 , , 三种情况进行讨论,即得.
【详解】若 ,原不等式为 ,则 ;
当 时,原不等式可化为 ,
若 ,原不等式可化为 ,解得 ;
若 ,原不等式可化为 ,解得 或 .
综上所述,当 时,不等式的解集为 ;当 时,不等式的解集为
;当 时,不等式的解集为 或 .