文档内容
哈三中 2023—2024 学年度下学期
高一学年期末考试数学试卷
考试说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.
考试时间为120分钟.
1.答题前,考生先将自己的姓名、准考证号码填写清楚.
2.选择题必须使用2B铅笔填涂,非选择题必须使用 0.5毫米黑色字迹签字笔书写,字体工
整,字迹清楚.
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、
试题卷上答题无效.
4.保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷(选择题,共58分)
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
符合题目要求.
1. ,则 ( )
A. B. C. D.
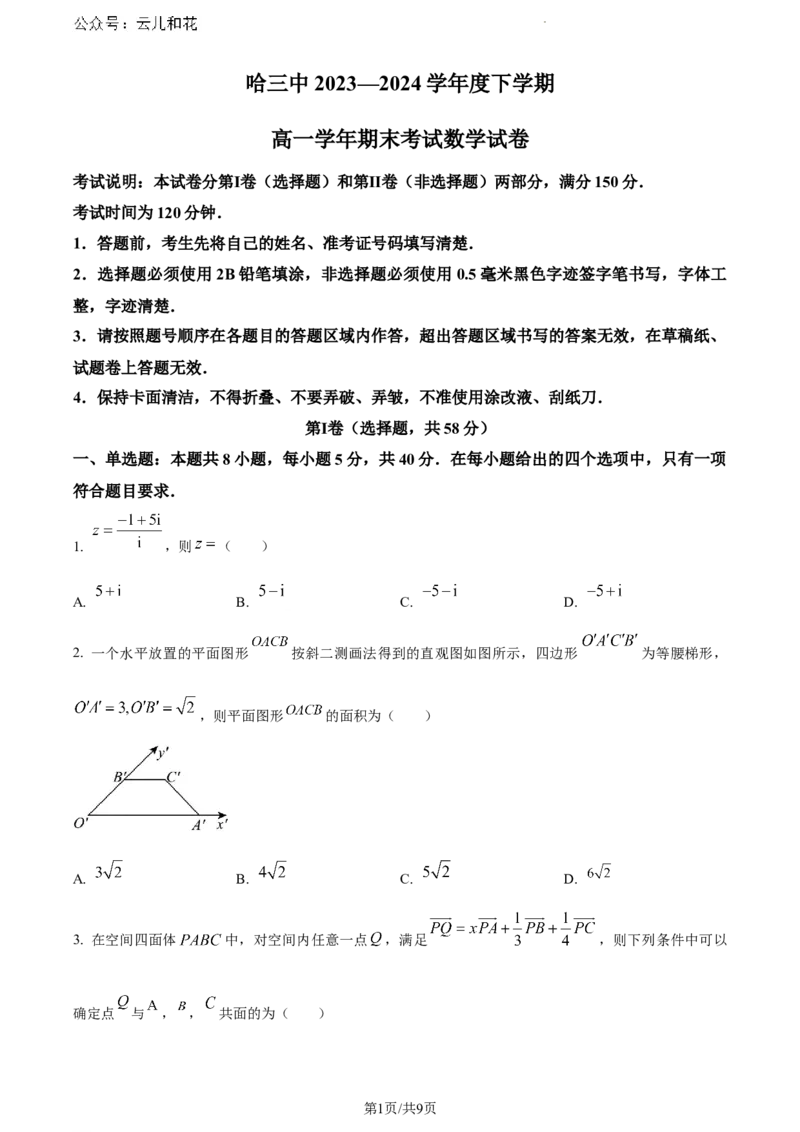
2. 一个水平放置的平面图形 按斜二测画法得到的直观图如图所示,四边形 为等腰梯形,
,则平面图形 的面积为( )
A. B. C. D.
3. 在空间四面体 中,对空间内任意一点 ,满足 ,则下列条件中可以
确定点 与 , , 共面的为( )
第1页/共9页
学科网(北京)股份有限公司A. B. C. D.
4. 已知向量 ,向量 为平面内两个不共线的单位向量,若 ,
,则下列结论正确的是( )
A. A、B、C三点共线 B. A、C、D三点共线
C. A、B、D三点共线 D. B、C、D三点共线
5. 经哈三中数学组集体备课研究,预计每周(五天)安排 8堂数学课,每天至少1堂,不同的安排方法有
( )
A. 35种 B. 126种 C. 495种 D. 1001种
6. 在 中,内角A,B,C所对的边分别为a,b,c,若 , ,则 的取值范围是(
)
A. B. C. D.
7. 三棱锥 的侧棱 是它的外接球的直径,且 ,则三棱锥
的体积为( )
.
A B. C. D.
8. 在 中, ,I是 的平分线上一点,且 ,若 内
(不包含边界)的一点D满足 ,则实数x的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
第2页/共9页
学科网(北京)股份有限公司9. 设m,n是不同的直线, 是不同的平面,则下列命题错误的是( )
A. 若 ,则 B. 若 ,则n平行于 内的无数条直线
C. 若 ,则 D. 若 ,则
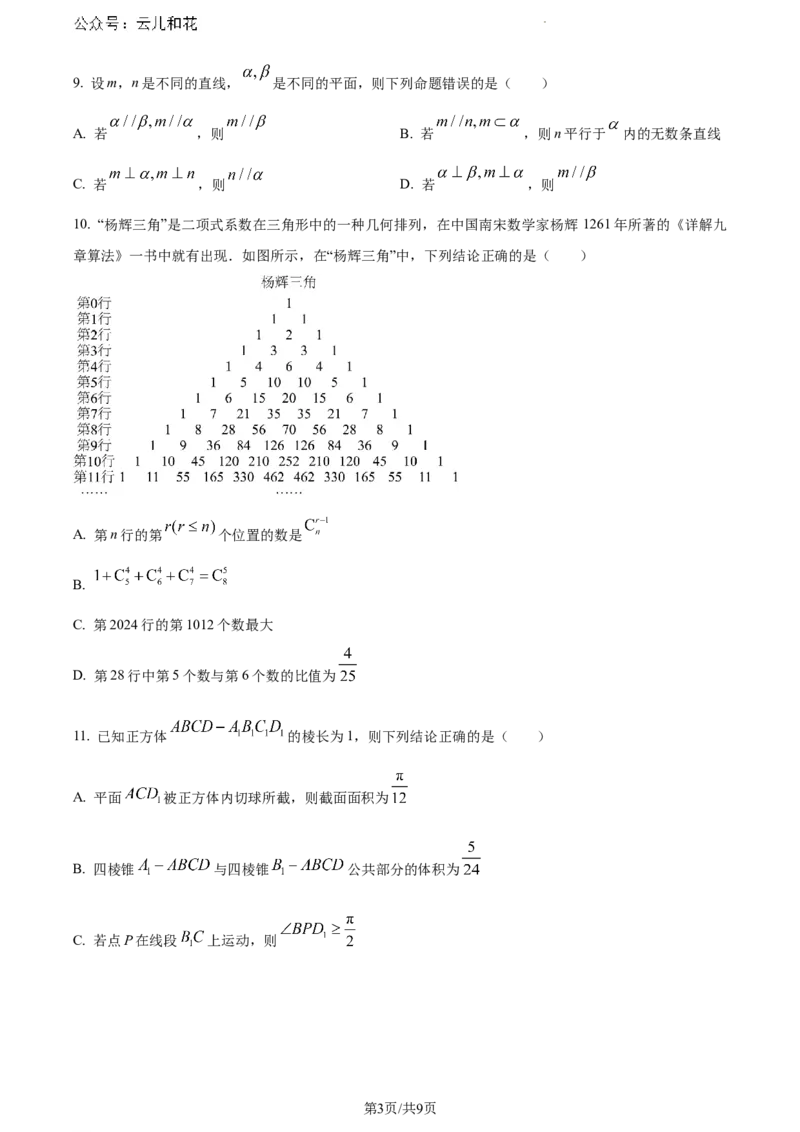
10. “杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉 1261年所著的《详解九
章算法》一书中就有出现.如图所示,在“杨辉三角”中,下列结论正确的是( )
A. 第n行的第 个位置的数是
B.
C. 第2024行的第1012个数最大
D. 第28行中第5个数与第6个数的比值为
11. 已知正方体 的棱长为1,则下列结论正确的是( )
A. 平面 被正方体内切球所截,则截面面积为
B. 四棱锥 与四棱锥 公共部分的体积为
C. 若点P在线段 上运动,则
第3页/共9页
学科网(北京)股份有限公司D. 以D为球心, 为半径作球,则球面与正方体 的表面的交线长为
第Ⅱ卷(非选择题,共92分)
三、填空题:本大题共3小题,每小题5分,共15分.
12. 正四棱锥 的所有棱长均为4,M为棱PC的中点,则异面直线BM与PA所成角的余弦值为
______.
13. 已知 ,则 ______.
14. 现用 种不同的颜色对四棱台 的 个顶点涂色,要求同一条棱的两个端点不同色,
且上底面 个顶点颜色都不同,则不同的涂色方法种数为______.(用具体数字作答)
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.
15. 的展开式中所有项的二项式系数之和为32,前3项的系数之和为31.
(1)求实数n和a的值;
(2)求 的展开式中 的系数.
16. 已知 的内角A,B,C所对的边分别为a,b,c,面积为S, ,
.
(1)求 ;
(2)从以下3个条件中选择1个作为已知条件,使 存在且唯一确定,求S.
的
条件① ;条件② ;条件③BC边上 中线长为 .
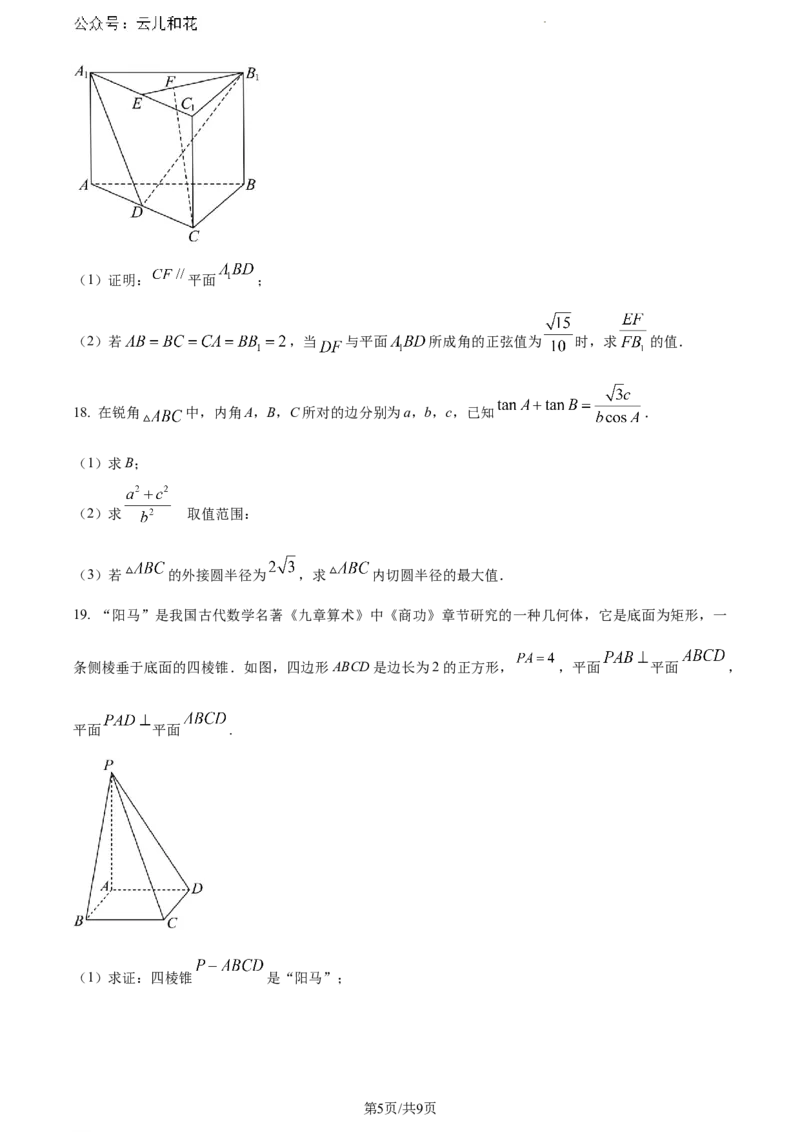
17. 在直三棱柱 中,D、E分别是棱 的中点,F为线段 上的点.
第4页/共9页
学科网(北京)股份有限公司(1)证明: 平面 ;
(2)若 ,当 与平面 所成角的正弦值为 时,求 的值.
18. 在锐角 中,内角A,B,C所对的边分别为a,b,c,已知 .
(1)求B;
(2)求 取的值范围:
(3)若 的外接圆半径为 ,求 内切圆半径的最大值.
19. “阳马”是我国古代数学名著《九章算术》中《商功》章节研究的一种几何体,它是底面为矩形,一
条侧棱垂于底面的四棱锥.如图,四边形ABCD是边长为2的正方形, ,平面 平面 ,
平面 平面 .
(1)求证:四棱锥 是“阳马”;
第5页/共9页
学科网(北京)股份有限公司(2)点M在正方形 内(包括边界).平面 平面 且 ,
(i)求M点轨迹长度;
(ii)是否存在M点,使得平面 平面 ,若存在,求二面角 的余弦值;若不存
在,请说明理由.
第6页/共9页
学科网(北京)股份有限公司哈三中 2023—2024 学年度下学期
高一学年期末考试数学试卷
考试说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.
考试时间为120分钟.
1.答题前,考生先将自己的姓名、准考证号码填写清楚.
2.选择题必须使用2B铅笔填涂,非选择题必须使用 0.5毫米黑色字迹签字笔书写,字体工
整,字迹清楚.
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、
试题卷上答题无效.
4.保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷(选择题,共58分)
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
符合题目要求.
【1题答案】
【答案】A
【2题答案】
【答案】B
【3题答案】
【答案】A
【4题答案】
【答案】C
【5题答案】
【答案】A
【6题答案】
【答案】B
【7题答案】
【答案】B
【8题答案】
【答案】B
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
第7页/共9页
学科网(北京)股份有限公司【9题答案】
【答案】ACD
【10题答案】
【答案】AB
【11题答案】
【答案】BCD
第Ⅱ卷(非选择题,共92分)
三、填空题:本大题共3小题,每小题5分,共15分.
【12题答案】
【答案】
【13题答案】
【答案】112
【14题答案】
【答案】
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.
【15题答案】
【答案】(1) ,
(2)
【16题答案】
【答案】(1)
(2)答案见详解
【17题答案】
【答案】(1)证明见解析
(2)
【18题答案】
【答案】(1)
第8页/共9页
学科网(北京)股份有限公司(2) 的取值范围为
(3)
【19题答案】
【答案】(1)证明见解析
(2)(i) ;(ii)存在,该点为 与 交点,二面角 的余弦值
第9页/共9页
学科网(北京)股份有限公司