文档内容
河北省 届高三年级大数据应用调研联合测评( )
2024 Ⅷ
数学参考答案及解析
题号
1 2 3 4 5 6 7 8 9 10 11
答案
A D C C D B C D BCD ABD ACD
. 【解析】z 4-i 3+5i 17+17i 1 1 复数z在复平面内对应的点所在的象限为第一象
1A = = 2 2 = + i,∴
3-5i 3+5i 3+5 2 2
限 故选
, A.
. 【解析】将P点坐标代入抛物线方程得p 故抛物线的准线方程为y 1.故选 .
2D =1, =- D
2
. 【解析】A B C 则 A B C 故选 .
3C =(-∞,-1], =(-2,2), =(-3,1), (∁ R )∩( ∩ )=(-1,1), C
. 【解析】如图 AN→ 1AC→ 1AM→ 1AC→ 1AB→ AN→ CB→ 1AC→ 1AB→ AB→ AC→
4C , = + = + , · = + - =
2 2 2 3 2 3
1AB→2 1AB→ AC→ 1AC→2 1 1 9 故选 .
+ · - =12+ ×6×3× - =9, C
3 6 2 6 2 2
a2
5 . D 【解析】设g ( x )=ax -3 + a , h ( x )=log a x2 +1- x ,∴ h (- x )=- h ( x ), h ( x ) 是奇函数 ,
-1
a2 a2
gx 也是奇函数 则g x gx -3 a -3 a 解得a 故选
∴ () , (- )=- (),a- x + =-ax - , =3, D.
-1 -1
. 【解析】取PC中点H 连接MH 交PN 于D PN MH PN 平面AMH AD PN D 是
6B , ,∴ ⊥ , ⊥ ,∴ ⊥ ,
2
PN的中点 PA AN 设 ABC的中心为O PO PA2 AO2 23 15V
,∴ = = 3, △ ,∴ = - = 3- = , =
3 3
1 3 2 15 5 故选
× ×2× = , B.
3 4 3 3
. 【解析】设切点为M 连接PF 由已知 OP OF OF PF PF OM PF OM
7C , 1, | |=| 2|=| 1|,∴ 1⊥ 2,∵ ⊥ 2,∴ ∥
b c
PF PF b PF a b b2 a b2 c2 a2 b2 2e 5.故选
1,| 1|= ,| 2|=2 - ,∴ +(2 - )=4 =4( - ),a= ,=a= C.
3 3
x x
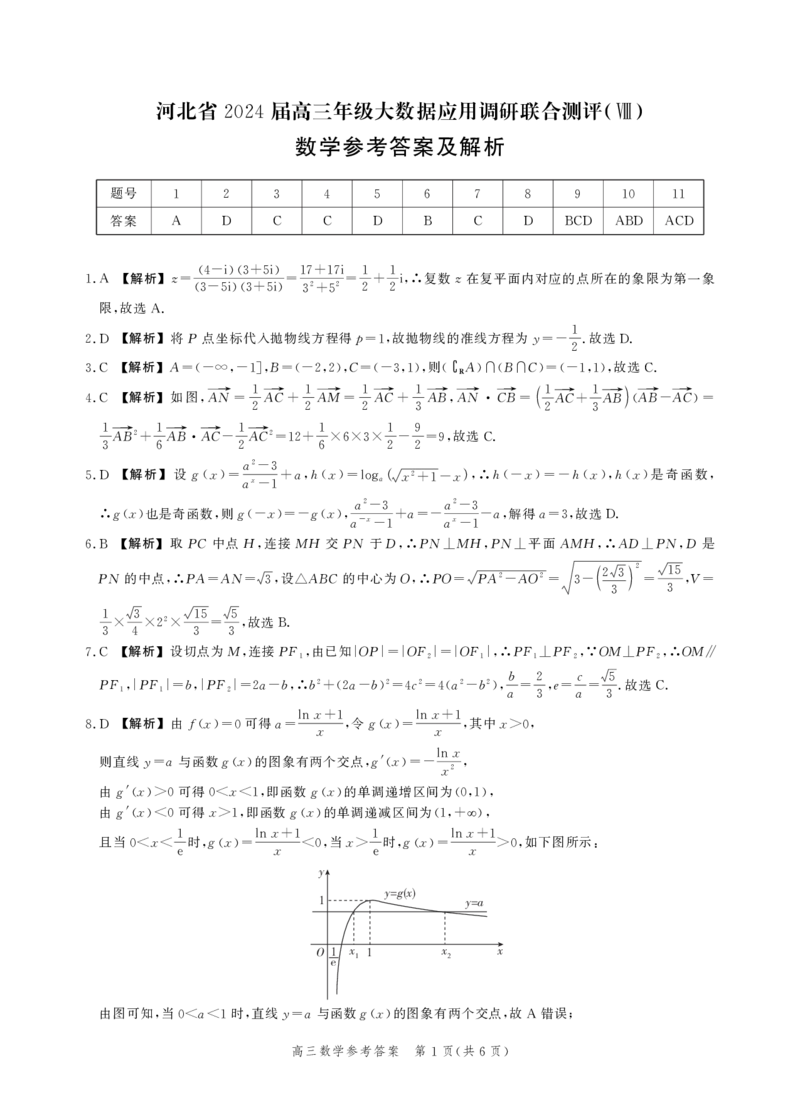
. 【解析】由fx 可得a ln +1 令gx ln +1 其中x
8D =0 = x , = x , >0,
x
则直线y a与函数gx 的图象有两个交点g'x ln
= , =-x2 ,
由g'x 可得 x 即函数gx 的单调递增区间为
>0 0< <1, 0,1 ,
由g'x 可得x 即函数gx 的单调递减区间为 ㄠ
<0 >1, 1,+ ,
x x
且当 x 1时gx ln +1 当x 1时gx ln +1 如下图所示
0< < , = x <0, > , = x >0, :
e e
Z
Z H Y
Z B
0 Y Y Y
F
由图可知 当 a 时 直线y a与函数gx 的图象有两个交点 故 错误
, 0< <1 , = , A ;
高三数学参考答案 第 页(共 页)
1 6由图可知 1 x x
, < 1<1< 2,
e
ax
因为f'x 1 a 1- 由f'x 可得 x 1 由f'x 可得x 1
=x- = x , >0 0< a,
所以 函数fx 的增区间为 1 减区间为 1 ㄠ 则必有 x 1 x
, 0,a , a,+ , 0< 1a,
令hx f 2 x fx 2 x a 2 x x ax 其中 x 1
= a- - =lna- - a- -ln + , 0< a =0, a- 1 - 1 >0, 1 < a- 1 ,
又fx 可得fx f 2 x
2 =0, 2 < a- 1 ,
因为函数fx 的单调递减区间为 1 ㄠ 则x 2 x 即x x 2 故 错误
a,+ , 2>a- 1, 1+ 2>a, B ;
ax x xx
由 1=ln 1+1 两式相加整理可得x x ln 1 2 +2 2
ax x , 1+ 2= a >a,
2=ln 2+1
所以 xx 可得x x 故 错误
,ln 1 2 >0, 1· 2>1, C ;
由图可知1 x x 则 x 又因为x 1 所以x x 1 故 正确.故选
< 1<1< 2, - 1>-1, 2>a, ,2- 1>a-1, D D.
e
. 【解析】gx 4x π π
9BCD ()=sin + -
3 4 6
高三数学参考答案 第 页(共 页)
2 6
4x π 4x π π 4x 2π
=sin + =-cos + + =-cos + ,
3 6 3 6 2 3 3
故 错误 由g π 得 正确 由g π 得 正确 由 k 4x 2π k 得 π
A ; =1, B ; - =0, C ; 2π≤ + ≤π+2π, - +
4 8 3 3 2
k k
3 x π 3 当k 时 π x π 故 正确.故选
π≤ ≤ + π, =0 ,- ≤ ≤ , D BCD.
2 4 2 2 4
2
10 . ABD 【解析】由 | PA |= 2| PB | 得 : x2 +( y - 2) 2 =2 x2 + y - 2
2
即x2 y2 面积为 , + =1, π,A
正确 点B在圆内 由图知 PB 最小值为 2 正确 过A向圆引切线 两条切线夹角为π 不正
; , | | 1- ,B , , ,C
2 2
确.过点 1 1 的直线与点P的轨迹交于点M N 则MN的最小值为 正确 故选
, , , 2,D , ABD.
2 2
. 【解析】由已知得a a a a 若d a a 正确 当d 时 S
11ACD m -1+ m +2= m+ m +1=0, <0,m>0,m +1<0,A ; <0 ,m
是S 的最大值 不正确 da a da a a a a a a
n ,B ;3 (m -1+ m +2)=3 (m+ m +1),∴(m +2- m -1)(m -1+ m +2)=3(m +1
-
a
m)(
a
m+
a
m +1),∴3
a2m+ a2m
+2=
a2m
-1+3
a2m
+1,C
正确
;
同理a
m -1+
a
m +1=-(
a
m +2+
a
m),
两边乘以
2
d得
(
a
m -1+
a
m +1)(
a
m +1-
a
m -1)=-(
a
m +2+
a
m)(
a
m +2-
a
m),
整理得a2m
-1+
a2m= a2m
+1+
a2m
+2,
故
D
正确.故选
ACD.
.【答案】 1
12 -
3
【解析】 α 2α 2α cos
2α
-sin
2α
1-tan
2α
1.
cos2 =cos -sin = 2α 2α= 2α=-
sin +cos 1+tan 3
.【答案】1
13
4【解析】方法一 令m a a a a a a a a q 1.
: =1,∴4(1+ 2+ 3)+ 1=5(1+ 2),2=4 3,=
4
S S m
方法二 :2 2 m ( S 3 m- S 2 m)= S 2 m- S m,∴ qm =S 3 2 m m - - S 2 m m = 1 4 ,∴ q = 1 4 .
.【答案】 分 1 分
14 10(2 ) (3 )
6
【解析】先将 排好 有三种排法 然后将三个 插入 对于 先将两个 中间插入一
122 , 122,212,221, 3 , 122, 2
个 将剩下的两个 插入三个空隙有 种插法 同理 也有 种插法 对于 四个空隙 插入
2
3, 3 C3=3 , ,221 3 , 212, ,
6
三个 有 3 种插法 共有 种.而这 个数组成的六位数共有 A6 种 其概率为10 1.
3, C4=4 , 10 6 2 3=60 , =
A2A3 60 6
.【解】 设 该同学对该题不会空选 为事件A 该同学选择两个选项 为事件B 且B A. 分
15 (1) “ ” ,“ ” , ⊂ …… 1
PA 1 3 7 分
( )=1- = ,…………………………………………………………………………………… 2
2 8
PB 2 1 3 3 分
( )=C3 = ,…………………………………………………………………………………… 3
2 8
PAB PB 分
( )= ( ), ………………………………………………………………………………………… 4
PAB
由条件概率 PBA ( ) 3. 分
, (| )=PA = ………………………………………………………………… 6
( ) 7
由已知 X 分
(2) , =0,3,6,…………………………………………………………………………………… 7
3
1
PX 2 1 分
( =6)=PA = , ………………………………………………………………………………… 8
( ) 7
3
1
2
PX 2 2 分
( =3)=PA = ,………………………………………………………………………………… 9
( ) 7
PX 4. 分
( =0)= …………………………………………………………………………………………… 10
7
其分布列为
X
0 3 6
分
……………………………………………………… 12
P 4 2 1
7 7 7
EX 4 2 1 12. 分
( )=0× +3× +6× = …………………………………………………………………… 13
7 7 7 7
.【解】 方法一 连接FC 交CE于H 连接DH 分
16 (1) : , 1 , , ………………………………………………… 1
BF 平面BFCBF 平面DEC
∵ ⊂ , ∥ 1,
平面BFC 平面DEC DH
∩ 1= ,
BF DH. 分
∴ ∥ ……………………………………………………………………………………………… 3
FH BD
分
∴HC=DC=1, ………………………………………………………………………………………… 4
FC EC
∵ 1∥ ,
FC EC 分
∴ 1= ,……………………………………………………………………………………………… 5
AF FC
∴ 1 =2 1,
F是AC 的靠近点C 的三等分点. 分
∴ 1 1 1 ………………………………………………………………… 6
方法二 取AE的中点G 连接BG
: , ,
BG DE 分
∴ ∥ , ……………………………………………………………………………………………… 1
过G作GF EC 交AC 于F 连接BF
∥ 1 1 1 , ,
高三数学参考答案 第 页(共 页)
3 6BG 平面DEC GF 平面DEC
∴ ∥ 1, ∥ 1,
平面BGF 平面DEC 分
∴ ∥ 1, ……………………………………………………………………………… 3
BF 平面DEC 分
∴ ∥ 1,……………………………………………………………………………………… 4
GE FC 1AC
1= 1 1,
3
F是AC 的靠近点C 的三等分点. 分
∴ 1 1 1 ………………………………………………………………… 6
答出AF FC 等也给分 [
( 1 =2 1 )
设棱长为 以DADB为xy轴建立如图所示的空间直角坐标系
(2) 6, 、 、 , " ' $
C C E F . 分
(0,-3,0),1(0,-3,6), (3,-2,0), (3,-2,6)………… 7
DC→ DE→ DF→ 分
∴ 1=(0,-3,6), =(3,-2,6), =(3,-2,6),……… 8 )
设平面DFC 的法向量为m x y z #
1 =(1,1,1),
m · DF→ =0, 3 x 1-2 y 1+6 z 1=0, Y ( &
∴ m DC→ y z " $
· 1=0, -3 1+61=0,
%
令x m 3 . 分
1=1,∴ = 1,- 3,- ………………………………… 10
2 #
Z
设平面DEC 的法向量为n x y z
1 =(2,2,2),
n · DE→ =0, 3 x 2-2 y 2=0,
∴n DC→ y z
· 1=0, -3 2+62=0,
令x n 3 . 分
2=2,∴ = 2,3, …………………………………………………………………………… 12
2
3
2-3-
所以 mn 4 -7 7 589 分
cos< ,>= = = ,……………………… 14
3 3 19· 31 589
1+3+ · 4+3+
4 4
所以平面DFC 与平面DEC 夹角的余弦值为7 589. 分
1 1 …………………………………………… 15
589
.【解】 在 ACD中 由正弦定理得
17 (1) △ , :
AC AD
ADC= ACD,
sin∠ sin∠
即 23 2 分
= ACD, ………………………………………………………………………………… 2
sin120° sin∠
解得 ACD 分
∠ =30°,………………………………………………………………………………………… 3
在 ABD中 由余弦定理得BD2 分
△ , =12+4-2×2×23cos150°=28,……………………………… 5
BD . 分
=27 ………………………………………………………………………………………………… 6
由已知 BAD θ ADB 分
(2) ∠ =120°+ ,∵∠ =15°,………………………………………………………… 7
AB BD
在 ABD中 分
∴ △ , = θ ,………………………………………………………………… 8
sin15° sin(120°+ )
θ
BD 23sin(120°+ ). 分
= ………………………………………………………………………………… 9
sin15°
DBA θ CBD θ
∠ =45°- ,∠ = -15°,
BDC BCD θ 分
∠ =105°,∠ =90°- ,……………………………………………………………………… 11
BC BD
在 BCD中 分
∴ △ , = θ ,……………………………………………………………… 12
sin105° sin(90°- )
θ θ
BD 6cos 23sin(120°+ ) 分
∴ = = ,…………………………………………………………………… 13
cos15° sin15°
高三数学参考答案 第 页(共 页)
4 6θ . 分
∴tan =6-33 ……………………………………………………………………………………… 15
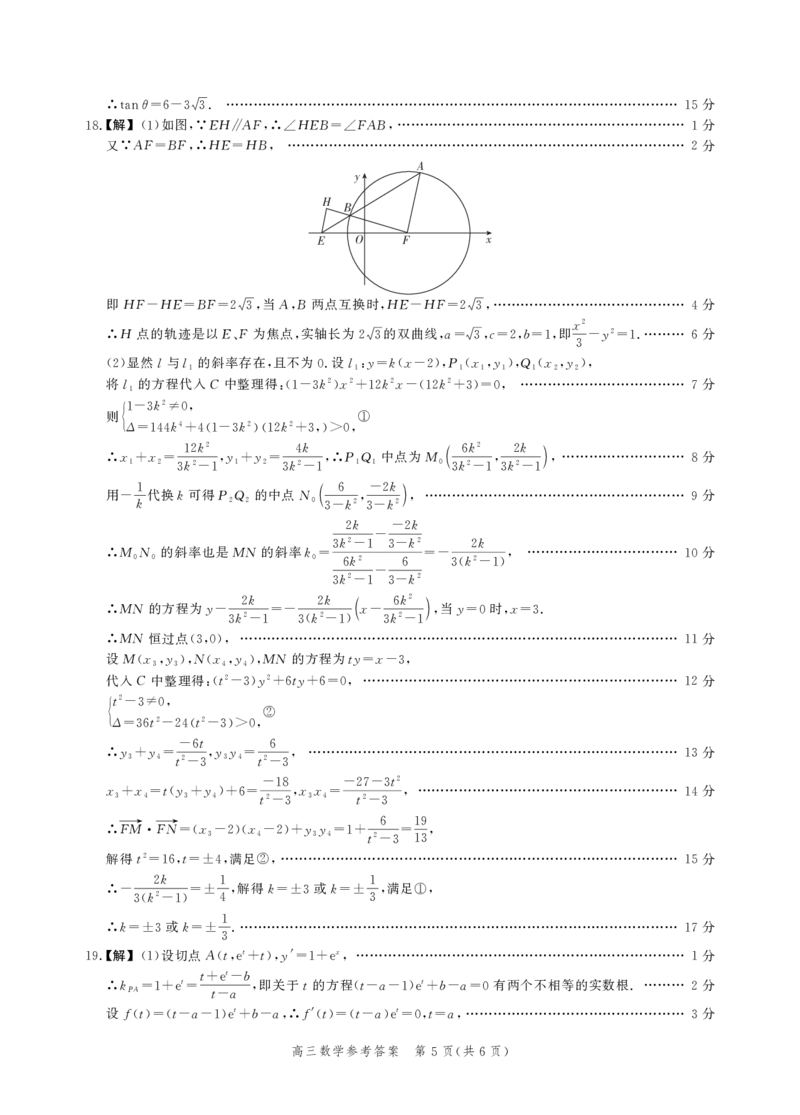
.【解】 如图 EH AF HEB FAB 分
18 (1) ,∵ ∥ ,∴∠ =∠ ,……………………………………………………… 1
又 AF BF HE HB 分
∵ = ,∴ = , …………………………………………………………………………… 2
"
Z
)
#
& 0 ' Y
即HF HE BF 当AB两点互换时 HE HF 分
- = =23, , , - =23,…………………………………… 4
x2
H 点的轨迹是以EF为焦点 实轴长为 的双曲线a c b 即 y2 . 分
∴ 、 , 23 ,= 3,=2,=1, - =1 ……… 6
3
显然l与l 的斜率存在 且不为 .设l y kx P x y Q x y
(2) 1 , 0 1:= (-2),1(1,1),1(2,2),
将l 的方程代入C中整理得 k2x2 k2x k2 分
1 :(1-3 ) +12 -(12 +3)=0, ……………………………… 7
k2
则 1-3 ≠0,
Δ k4 k2 k2 ①
=144 +4 1-3 12 +3, >0,
k2 k k2 k
x x 12 y y 4 PQ 中点为M 6 2 分
∴ 1+ 2=k2 ,1+ 2=k2 ,∴ 1 1 0 k2 ,k2 ,……………………… 8
3 -1 3 -1 3 -13 -1
k
用 1代换k可得PQ 的中点N 6 -2 分
-k 2 2 0 k2 , k2 ,………………………………………………… 9
3- 3-
k k
2 -2
k2 - k2 k
MN 的斜率也是MN的斜率k 3 -1 3- 2 分
∴ 0 0 0= k2 =- k2 , …………………………… 10
6 6 3( -1)
k2 - k2
3 -1 3-
k k k2
MN的方程为y 2 2 x 6 当y 时x .
∴ -k2 =- k2 -k2 , =0 ,=3
3 -1 3( -1) 3 -1
MN恒过点 分
∴ (3,0),…………………………………………………………………………………… 11
设Mx y Nx y MN的方程为ty x
(3,3), (4,4), = -3,
代入C中整理得 t2 y2 ty 分
:( -3) +6 +6=0,…………………………………………………………… 12
t2
-3≠0,
Δ t2 t2 ②
=36 -24 -3 >0,
t
y y -6 yy 6 分
∴ 3+ 4=t2 ,3 4=t2 , ……………………………………………………………………… 13
-3 -3
t2
x x ty y -18xx -27-3 分
3+ 4= (3+ 4)+6=t2 ,3 4= t2 ,………………………………………………… 14
-3 -3
FM→ FN→ x x yy 6 19
∴ · =(3-2)(4-2)+ 3 4=1+t2 = ,
-3 13
解得t2 t 满足 分
=16,=±4, ②,…………………………………………………………………………… 15
k
2 1 解得k 或k 1 满足
∴- k2 =± , =±3 =± , ①,
3( -1) 4 3
k 或k 1. 分
∴ =±3 =± …………………………………………………………………………………… 17
3
.【解】 设切点At t t y' x 分
19 (1) (,e+ ), =1+e,……………………………………………………………… 1
t t b
k t +e- 即关于t的方程t a t b a 有两个不相等的实数根. 分
∴ PA=1+e= t a , (- -1)e+ - =0 ……… 2
-
设ft t a t b a f't t a t t a 分
()=(- -1)e+ - ,∴ ()=(- )e=0,= ,………………………………………… 3
高三数学参考答案 第 页(共 页)
5 6故ft在t a处取得极小值也是最小值fa b a a 分
() = ()= - -e,………………………………………… 4
当t 时ft 当t 时ft b a 若满足方程有两个不相等的实数根
→+∞ , ()→+∞, →-∞ , ()→ - , ,
b a
则 - >0, 分
b a a ………………………………………………………………………………………… 5
- -e<0,
b a aa b a ab a b a b a 分
∴0< - ln(- ),(- )>(- )ln(- ), ………………………………………… 6
设gx x x g'x x x 1 分
()= ln ,∴ ()=1+ln =0,= ,……………………………………………………… 7
e
gx 在x 1处取得最小值g 1 1 ab a 1. 分
∴ () = =- ,∴ (- )>- …………………………………… 8
e e e e
设Ax y Bx y y 1y y 1 x 1 x 2 x . 分
(2) (1,1), (2,2),∴ 0= (1+ 2)= (e +e )+ 0 ……………………………… 9
2 2
b a b a
由 知x a - x a - 分
(1) ,1-(+1)+ x =0,2-(+1)+ x =0, ………………………………………… 10
1 2
e e
x x
x x 1+ 2
两式相减整理得b a (1- 2)e 分
:- = x x , …………………………………………………………… 11
1 2
e -e
( b - a )-( y 0- x 0)= ( x 1 e - x x 1 - 2 e )e x x 2 1+ x 2 - 1 2 (e x 1 +e x 2 )= 2(e e x x 1 1 - + x e 2 x 2 ) 2( x 1- x 2)- e 2 e x 1 x 1 - + e x 2 2 x 2
高三数学参考答案 第 页(共 页)
6 6
=
x x
1+ 2 x x
e x x 1- 2 1
x 1 x 2 2(1- 2)-e - x 1- x 2
2(e -e ) e
分
,…………………………………………………………… 13
x x
1+ 2
不妨设x x m x x e 则hm m m - m 分
1> 2, = 1- 2>0,∴ x x >0, ( )=2 -(e -e ),………………… 14
1 2
2(e -e )
h'm m - m 分
( )=2-(e +e )≤2-2=0, …………………………………………………………………… 15
hm 在m 上单调递减 hm h 分
∴ ( ) ∈(0,+∞) ,∴ ( )< (0)=0,…………………………………………… 16
b a y x 即a y b x . 分
∴(- )-(0- 0)<0, + 0> + 0 ………………………………………………………… 17