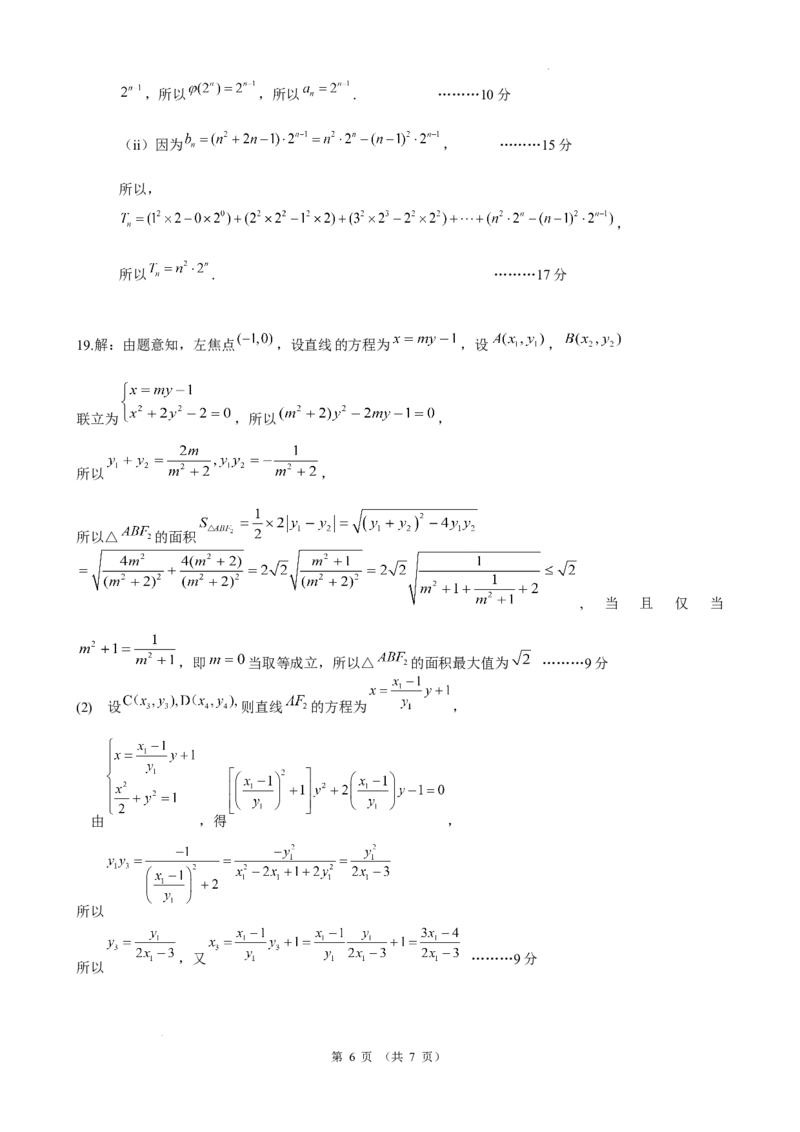文档内容
昆明一中 2024 届高三第十次联考
数学参考答案
命题、审题组教师 杨昆华 彭力 李文清 李春宣 丁茵 王在方 张远雄 李露 陈泳序 杨耕耘
一、选择题
题号 1 2 3 4 5 6 7 8
答案 A B C C D B B A
1.解析:在两个变量 与 的回归模型中,它们的决定系数 越接近 ,模型拟合效果越好,在四个选
项中A的决定系数最大,所以拟合效果最好的是模型 ,选A.
2.解析:由二项展开式,知其通项为 ,,令 ,解得 ,
所以 的系数为 ,选B.
3.解析:因为函数 是奇函数,所以 ,即 ,
,即 ,所以 ,选C.
4.解析:对于A,由 且 ,则 是平面 和平面 的公共点,又 ,由基本事实3可得
,故A正确;
对于B,由基本事实1:过不在一条直线上的三个点,有且只有一个平面,又 , 且 , ,
,则 ,故B正确;
对于C,由于平面 和平面 位置不确定,则直线 与直线 位置亦不确定,可能异面、相交、平行、重
合,故C错误;
对于D,由基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内,故D正确.
选C.
5.解析: ,选
D.
6.解析:已知圆 的圆心为 ,半径 ,若直线 上存在两点 , ,
使得 恒成立,则以 为直径的圆要内含或内切圆 ,点 到直线 的距离
第 1 页 (共 7 页)
学科网(北京)股份有限公司,所以 长度的最小值为 ,选B.
7.解析:设 ,因为 ,所以 ,由椭圆的定义可得 , ,
因为 ,所以 ,在 △ 中,有 ,解得 ,
在 △ 中,有 ,整理得 ,选B.
8.解析:先将卡片分为符合条件的三份,由题意知,三人分六张卡片,且每人至少一张,至多四张,若
分得的卡片超过一张,则必须是连号.相当于将 , , , , , 这六个数用两个隔板隔开,在五个
空位插上两个隔板,共 种情况,再对应到三个人有 种情况,则共有 种分法,选
A.
二、多选题
题号 9 10 11
答案 CD ACD AB
9.解析:由题意, ,可知A,B错误;C,D正确,选CD.
10.解析:对于A,因为 ,且 是 的一个复数根,
所以 ,A正确
对于 B,因为 ,即 ,所以 ,解得 ,所以
, ,B错误
对于C,因为 ,而 ,即 , ,则复数 对应的点位于第二象限,
C正确;
对于D,因为 , ,所以复数 ( )在复平面内对应的点
的轨迹是半径为1的半圆,D正确
选ACD.
11.解析: 如图所示,令 ,则 ,若方程有
第 2 页 (共 7 页)
学科网(北京)股份有限公司五个不相等的实数根,设 有两个零点分别为 , ,则 ,即 得 ,则
,则实数 的取值范围是 ,选A B.
三、填空题
12.解析: .
13.解析:设点 ,由已知得 ,整理得 ,所以点 的轨迹方程为
,(如果方程为 ,给3分).
14.解析:因为 ,所以 ,
所以 ,所以 ,由正弦定理得: .
由余弦定理得: ,又由 得: ,
所以 (当且仅当 ,即△
为正三角形时,取“ ”),
因为 ,所以 的最大值为 .
四、解答题
15.解:(1)记 “甲跑第一棒”为事件 ,“甲跑第二棒”为事件 ,“甲跑第三棒”为事件 ,
“甲跑第四棒”为事件 ,“运动队获胜”为事件 .
则
.
所以当甲出场比赛时,该运动队获胜的概率为 . ………7分
(2) .
第 3 页 (共 7 页)
学科网(北京)股份有限公司所以当甲出场比赛时,在该运动队获胜的条件下,甲跑第一棒的概率为 . ………13分
16.解:(1)如图2,取 的中点 , 的中点 , 的中点 ,
连接 , , , , ,则 ,
z
因为△ 是等边三角形,所以 ,
C B
A
又平面 平面 ,平面 平面 ,
所以 平面 ,同理 平面 ,
O F
Q
所以 ,显然 ,所以四边形 是矩形, D E y
x
P
所以 ,
所以 ,则 , , , 四点共面. ………7分
(2)由(1)同理知 平面 ,如图建立空间直角坐标系 ,
由题知 , , , ,
所以 , ,设平面 的法向量为 ,
则 ,所以 ,
设平面 的一个法向量为 ,
所以 , 设平面 与平面 夹角为 ,
则 ,
平面 与平面 夹角的正弦值为 . ………15分
第 4 页 (共 7 页)
学科网(北京)股份有限公司17.解:(1) 的定义域为 , ,
令 解得 ,又因为当 时, 为增函数,
故当 时, ,则 在 上单调递减;
当 时, ,则 在 上单调递增;
故 ,故 . …………7分
(2) , ,则 ,
故当 时, ,则 在 单调递增;
当 时, ,则 在 单调递减;
故 .
又因为 ,所以 (当且仅当 时,取“ ”)
所以 . …………15分
18.解:(1)依题意可得: 表示所有不超过正整数 ,且与 互质的正整数的个数,
因为与 互质的数为 ,所以 ;
因为与 互质的数为 , ,所以 ;
因为与 互质的数为 , ,所以 . ………6分
(2)(i)因为 中与 互质的正整数只有奇数,所以 中与 互质的正整数个数为
第 5 页 (共 7 页)
学科网(北京)股份有限公司,所以 ,所以 . ………10分
(ii)因为 , ………15分
所以,
,
所以 . ………17分
19.解:由题意知,左焦点 ,设直线的方程为 ,设 ,
联立为 ,所以 ,
所以 ,
所以△ 的面积
, 当 且 仅 当
,即 当取等成立,所以△ 的面积最大值为 ………9分
(2) 设 则直线 的方程为 ,
由 ,得 ,
所以
,又 ………9分
所以
第 6 页 (共 7 页)
学科网(北京)股份有限公司同理 , ………10分
因为 三点共线,则 ,所以 ,
直线 的方程为 ,由对称性可知,直线 的定点在 轴上,所以令
得,
,所以直线 过定点 ………17分
第 7 页 (共 7 页)
学科网(北京)股份有限公司