文档内容
泸州市龙马潭区高 2023 级高二上期半期考试
数学试题
注意事项:
1.答卷前考生务必把自己的姓名、准考证号填写在答题卡上.
2.回答选择题时用2B铅笔将答题卡上对应题目的答案标号涂黑;回答非选择题时,用0.5毫
米黑色墨迹签字笔将答案写在答题卡上,写在本试卷上无效.
3.试卷满分150分,考试时间150分钟,考试结束后将本试卷和答题卡一并交回.
第I卷(选择题)
一、单选题(共40分)
1. 直线 的倾斜角是( )
A. B. C. D.
【答案】B
【解析】
【
分析】求得斜率,然后求得倾斜角.
【详解】直线的斜率为 ,对应的倾斜角为 .
故选:B
2. 已知实数 , 满足 ,则下列不等式恒成立的是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据函数的性质判断即可.
【详解】因为 , 是定义在 上的偶函数,
所以当实数 满足 时, , 不一定成立,故 不符合题意;因为 是定义在 上单调递增的奇函数,
所以当实数 满足 时,则 ,故 符合题意;
因为 在 上单调递减,
所以当实数 满足 时, 不一定成立,不符合题意.
故选: .
【点睛】判断不等式恒成立问题,方法有以下几种:1、可借助函数的单调性判断;2、可带特殊值说明不
等式不成立;3、根据不等式关性质判断;4、作差比较大小;5、作商比较大小.对于选择题我们一般采用
排除法.
3. 直线 : 和 : 垂直,则实数
.
A -1 B. 1 C. -1或1 D. 3
【答案】A
【解析】
【分析】 不合题意,由方程求出两直线的斜率,利用斜率之积为 即可得结果.
【详解】因为直线 : 和 : 垂直( 不合题意),
两直线的斜率分别为 ,
所以 ,解得a=-1,故选A.
【点睛】本题主要考查直线的方程,两条直线垂直与斜率的关系,属于简单题. 对直线位置关系的考查是
热点命题方向之一,这类问题以简单题为主,在斜率存在的前提下, (
),这类问题尽管简单却容易出错,特别是容易遗忘斜率不存在的情况,这
一点一定不能掉以轻心.
4. ,“直线 和直线 平行”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件 D. 既不充分也不必要条件
【答案】C
【解析】
【分析】求出两直线平行时 的值,再根据充分必要条件的定义判断.
【详解】由题意 ,则 , ,
因此题中应为充分必要条件.
故选:C.
5. 已知ΔABC的内角 所对的边分别为 ,若 ,
,则 ( )
A. B. C. D.
【答案】D
【解析】
【 分 析 】 由 , 利 用 诱 导 公 式 以 及 两 角 和 的 正 弦 公 式 可 得
,再利用余弦定理解方程求解即可.
【详解】由 ,
得 ,
即
,
得 ,
因为 ,
所以 ,
化为 ,得 ,故选D.
【点睛】本题主要考查两角和的正弦公式以及余弦定理解三角形,属于中档题. 对余弦定理一定要熟记两种形式:(1) ;(2) ,同时还要熟练掌握运用两种形式的
条件.另外,在解与三角形、三角函数有关的问题时,还需要记住 等特殊角的三角函数值,以
便在解题中直接应用.
6. 若 , 满足约束条件 ,则 的最小值为( )
A. -1 B. 0 C. D. 1
【答案】C
【解析】
【分析】作出满足不等式组的可行域,由 可得 ,可得 为该直线在 轴上的截距,
截距越大, 越小,结合图形可求 的最小值.
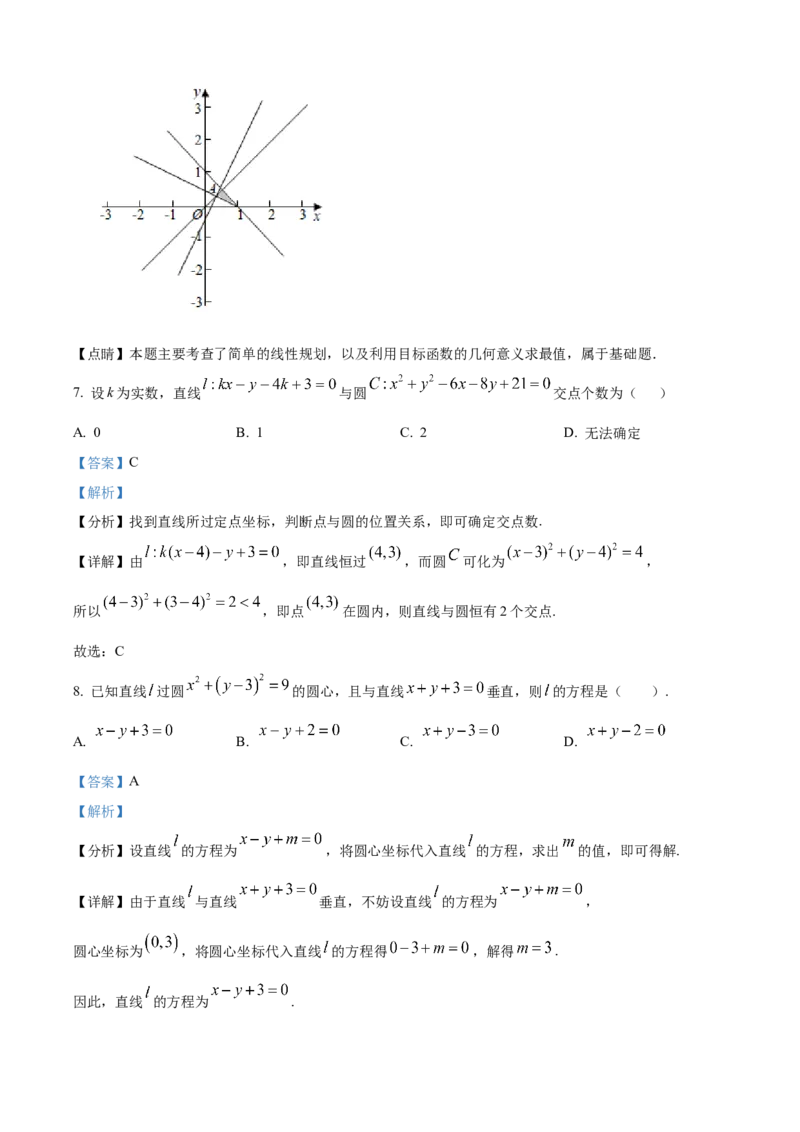
【详解】解:作出 , 满足约束条件 所表示的平面区域,如图所示:
由于 可得 ,可得 为该直线在 轴上的截距,截距越大, 越小,
作直线 ,然后把直线 向平面区域平移,
由图可知,直线平移到点 时, 最小,
由 可得 ,
即当直线 经过点 时, 取得最小值,
所以 .
故选:C.【点睛】本题主要考查了简单的线性规划,以及利用目标函数的几何意义求最值,属于基础题.
7. 设k为实数,直线 与圆 交点个数为( )
A. 0 B. 1 C. 2 D. 无法确定
【答案】C
【解析】
【分析】找到直线所过定点坐标,判断点与圆的位置关系,即可确定交点数.
【详解】由 ,即直线恒过 ,而圆 可化为 ,
所以 ,即点 在圆内,则直线与圆恒有2个交点.
故选:C
8. 已知直线 过圆 的圆心,且与直线 垂直,则 的方程是( ).
A. B. C. D.
【答案】A
【解析】
【分析】设直线 的方程为 ,将圆心坐标代入直线 的方程,求出 的值,即可得解.
【详解】由于直线 与直线 垂直,不妨设直线 的方程为 ,
圆心坐标为 ,将圆心坐标代入直线 的方程得 ,解得 .
因此,直线 的方程为 .故选:A.
二、多选题(共18分)
9. 已知椭圆 的左、右焦点分别为 ,点 在 上,且 的最大值为3,
最小值为1,则( )
A. 椭圆 的离心率为
B. 的周长为6
C. 若 ,则 的面积为3
D. 若 ,则
【答案】ABD
【解析】
【分析】对A,根据题意可得 , 即可求解;对B,根据椭圆的定义判断即可;对C,根
据余弦定理结合椭圆的定义判断即可;对D,根据余弦定理与椭圆的定义求解即可.
【详解】对A,由题意 , ,故 , ,故A正确;
对B, 的周长为 ,故B正确;
对C, ,
,当且仅当 时,等号成立,
因为 在 上递减,所以此时 最大,又 , ,所以 的最大值为 ,
,不成立,故C错误;
对D,由余弦定理,即 ,
解得 ,故 ,故D正确;
故选:ABD
10. 已知正方体 的棱长为4,点 为平面 内一动点,则下列说法正确的是(
)
A. 若点 在棱 上运动,则 的最小值为
B. 若点 是棱 的中点,则平面 截正方体所得截面的周长为
C. 若点 满足 ,则动点 的轨迹是一条直线
D. 若点 在直线 上运动,则 到直线 的最小距离为
【答案】BCD
【解析】
【分析】A项,由展开图转化为平面两点间距离最短问题可得最小值;B项,先作辅助线取中点找截面,
由平行四边形得线线平行,利用中位线的平行关系及空间平行的传递性证明所找截面即为所求,进而求周
长可得;C项,利用“过一点与已知直线垂直的直线在过该点与已知直线垂直的平面内”结论,可得两平
面的交线即为轨迹;D项,建立空间直角坐标系,求利用向量方法点线距可得.
【详解】A项,如图将平面 展开与平面 处于一个平面,
连接 与 交于点 ,
由图形知 ,当且仅当 三点共线时,等号成立.
即此时 取得最小值,
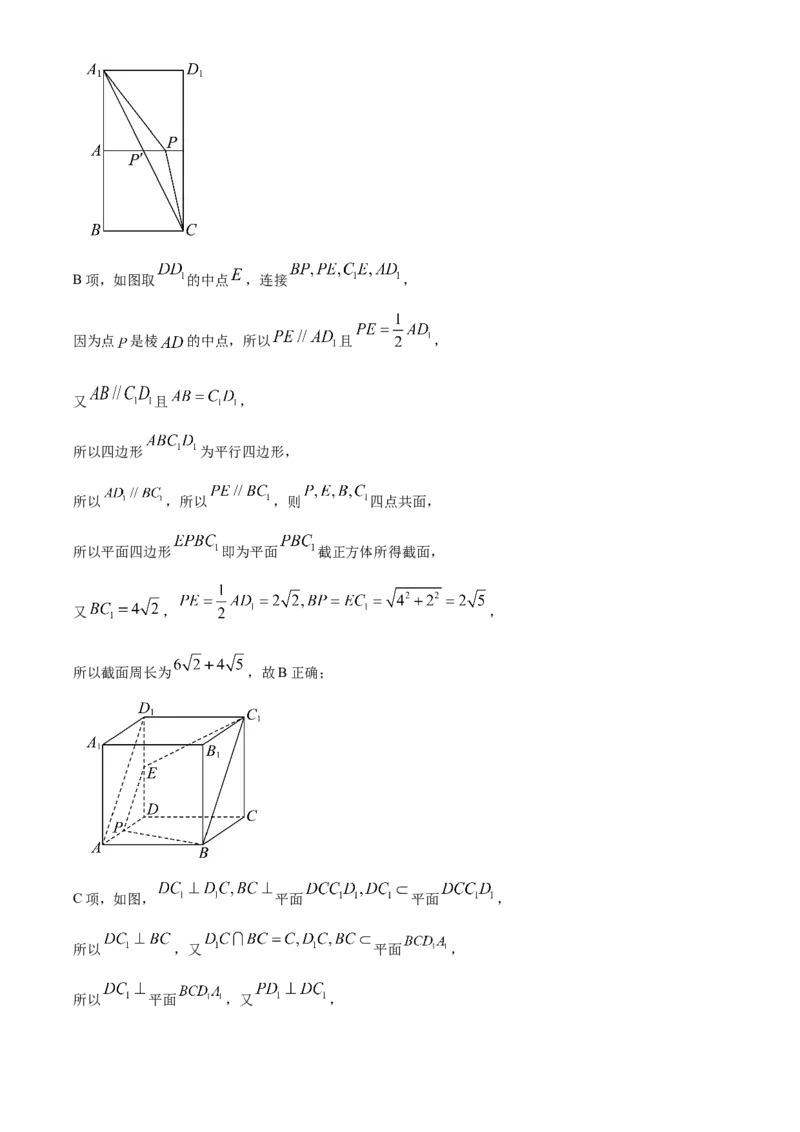
即 ,故A错误;B项,如图取 的中点 ,连接 ,
因为点 是棱 的中点,所以 且 ,
又 且 ,
所以四边形 为平行四边形,
所以 ,所以 ,则 四点共面,
所以平面四边形 即为平面 截正方体所得截面,
又 , ,
所以截面周长为 ,故B正确;
C项,如图, 平面 平面 ,
所以 ,又 平面 ,
所以 平面 ,又 ,故过 与 垂直的直线 在过 与直线 垂直的平面 内,
因为平面 平面 平面 ,且 平面 ,
所以 在直线 上,
即动点 的轨迹是一条直线,故C正确;
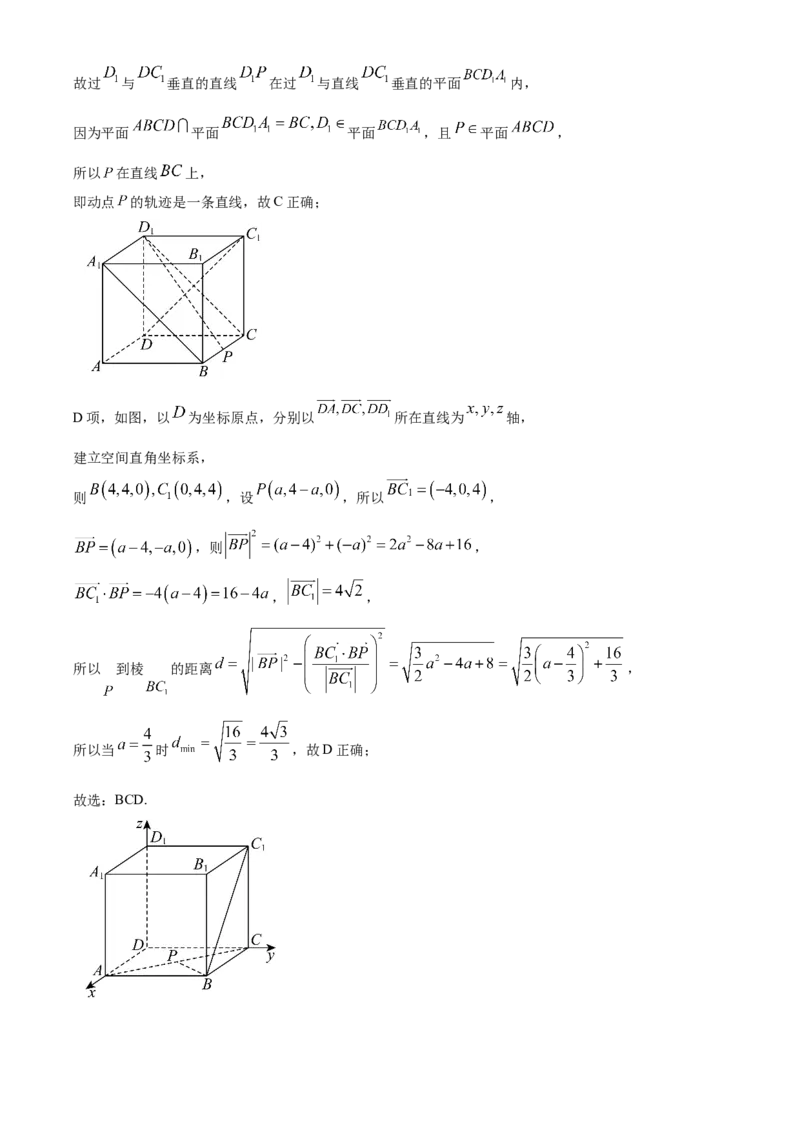
D项,如图,以 为坐标原点,分别以 所在直线为 轴,
建立空间直角坐标系,
则 ,设 ,所以 ,
,则 ,
, ,
所以 到棱 的距离 ,
所以当 时 ,故D正确;
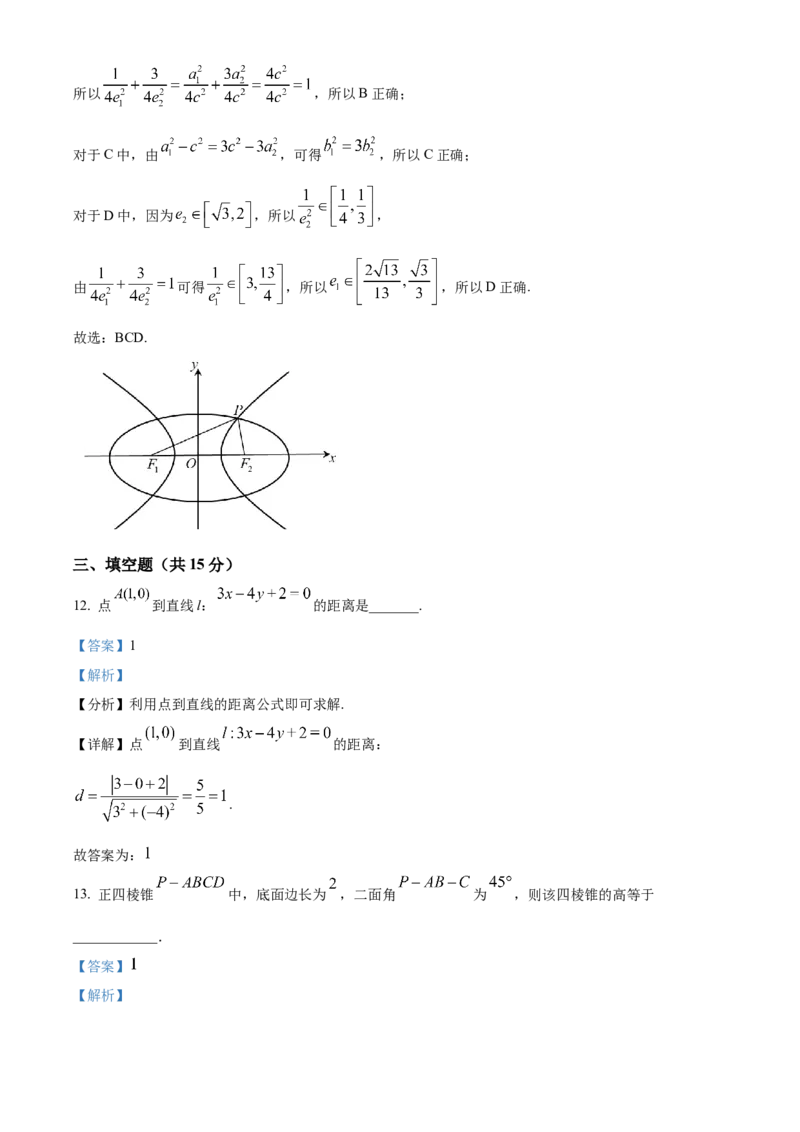
故选:BCD.11. 已知椭圆 的离心率为 ,双曲线 的离心率为 ,
两曲线有公共焦点 是椭圆与双曲线的一个公共点, ,以下结论正确的是( )
A.
B.
C.
D. 若 ,则
【答案】BCD
【解析】
【分析】根据焦距相等可判断A;根据椭圆和双曲线定义,结合余弦定理整理可判断B;根据B中
变形可判断C;由B中结论,结合 的范围可判断D.
【详解】根据题意,设 ,
对于A中,因为椭圆与双曲线有公共焦点,可得 ,所以 ,
即 ,所以A错误;
对于B中,不妨设点P在第一象限,由椭圆和双曲线的定义,可得 ,
所以 ,
又由余弦定理得 ,
可得 ,所以 ,所以B正确;
对于C中,由 ,可得 ,所以C正确;
对于D中,因为 ,所以 ,
由 可得 ,所以 ,所以D正确.
故选:BCD.
三、填空题(共15分)
12. 点 到直线l: 的距离是_______.
【答案】1
【解析】
【分析】利用点到直线的距离公式即可求解.
【详解】点 到直线 的距离:
.
故答案为:
13. 正四棱锥 中,底面边长为 ,二面角 为 ,则该四棱锥的高等于
____________.
【答案】
【解析】【分析】根据题意,画出直观图,根据二面角的平面角的定义,找到其平面角为 ,在 计
算 即为四棱锥的高.
【详解】如图所示,
取 的中点为 ,底面中心为 ,连接 ,
因为四棱锥 为正四棱锥,所以 ,
中, ,底面 为正方形,故 ,
所以 是二面角 的平面角,即 ,
又在 中, ,所以 ,即该四棱锥的高为 .
故答案为: .
14. 在平面直角坐标系 中,圆 经过点 ,则圆 上的点到原点的距离的最大值为
___________.
【答案】
【解析】
【分析】由已知条件计算出经过三点的圆 的直径,即可计算出圆上的点到原点距离最大值.
【详解】解:记 ,圆 经过点O,A,B.则 , ,,所以 ,故 为圆 的直径.从而圆 上的点到原点O的距离的最大值为
.
故答案为:
四、解答题(共77分)
15. 根据下列给定的条件,判断直线 与直线 是否平行.
(1) 的倾斜角为60°, 经过点 , ;
(2) 平行于y轴, 经过点 , .
【答案】(1) 或 与 重合
(2)
【解析】
【分析】(1)根据两直线的斜率关系即可判断位置关系,
(2)根据两直线均无斜率即可判断位置关系.
【小问1详解】
由题意,知直线 的斜率 ,
直线 的斜率 ,
所以 ,所以 或 与 重合.
【小问2详解】
由题意,知 是y轴所在的直线,所以 .
16. 为创建全国文明城市,宁德市进行“礼让斑马线”交通专项整治活动,按交通法规定:机动车行经人
行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行.下表是2020年宁德市某一主干路口
监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为,其中违章情况统计数据如下表:
月份 1 2 3 4 5违章驾驶员人数 100 85 80 70 65
(1)请利用所给数据求违章人数y与月份x之间的回归直线方程 ;
(2)预测该路口2020年9月份的不“礼让斑马线”违章驾驶员人数;并估计该路口经过几个月后“不礼
让”的不文明行为可以消失.
参考公式: , ,参考数据: .
【答案】(1) ;(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数为29,经过
13个月“不礼让”的不文明行为可以消失.
【解析】
【分析】
(1)首先求 , ,根据参考公式,分别求 和 ,求解回归直线方程;(2)令 代入回归直线方
程,求 的预报值,并令 ,求 .
【详解】(1)由表中数据知,
∴
即 ,
∴所求回归直线方程为.
(2) 令 ,则 人.
令 得
答:预测该路口9月份的不“礼让斑马线”违章驾驶员人数为21,故估计经过13个月“不礼让”的不文
明行为可以消失.17. 已知双曲线C: 经过点 ,其中一条渐近线为 ,O为坐标
原点.
(1)求C的标准方程;
(2)过C的右焦点F,且在 轴上的截距为 的直线 ,交 于P,Q两点,求 的值.
【答案】(1)
(2)7
【解析】
【分析】(1)根据渐近线方程以及点的坐标得到关于 的方程组,由此求解出 即可知C的标准方
程;
(2)根据条件先求出 的方程,然后联立 与双曲线的方程得到对应坐标的韦达定理形式,再将
表示为坐标形式即可求解出结果.
【小问1详解】
因为双曲线 的渐近线方程为 ,所以 ①,
又因为点 在双曲线上,所以 ②,
①②联立解得 ,所以双曲线 的方程为 .
【小问2详解】
由(1)可知双曲线 中 ,
所以右焦点 坐标为 ,即直线 的横截距为2,
又因为直线 在 轴上的截距为 ,所以直线 的方程为 ,即 ,联立 得 ,
设 ,则 ,
所以 .
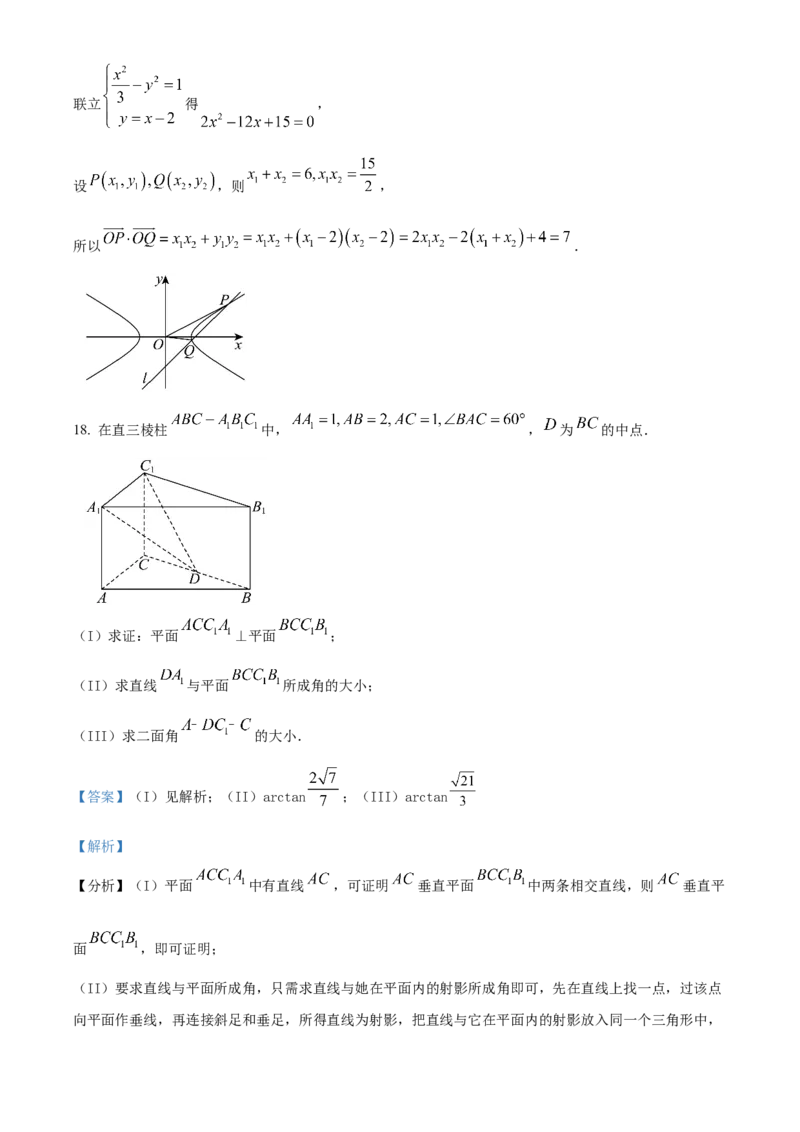
18. 在直三棱柱 中, , 为 的中点.
(I)求证:平面 ⊥平面 ;
(II)求直线 与平面 所成角的大小;
(III)求二面角 的大小.
【答案】(I)见解析;(II)arctan ;(III)arctan
【解析】
【分析】(I)平面 中有直线 ,可证明 垂直平面 中两条相交直线,则 垂直平
面 ,即可证明;
(II)要求直线与平面所成角,只需求直线与她在平面内的射影所成角即可,先在直线上找一点,过该点
向平面作垂线,再连接斜足和垂足,所得直线为射影,把直线与它在平面内的射影放入同一个三角形中,利用解三角形,求出线面角.
(III)求二面角的平面角的大小,可用三垂线法找到二面角的平面角,再放到一个三角形中,通过解三
角形,得出结果.
【详解】
(I)在△ABC中,由余弦定理,得,BC= ,
为直三棱柱, 平面 .
平面 , 平面 平面 .
(II) ,由(I)知, 平面 为直线 与平面 所成的角.
在 中, = = ,
故直线DA 与平面 所成角为
1
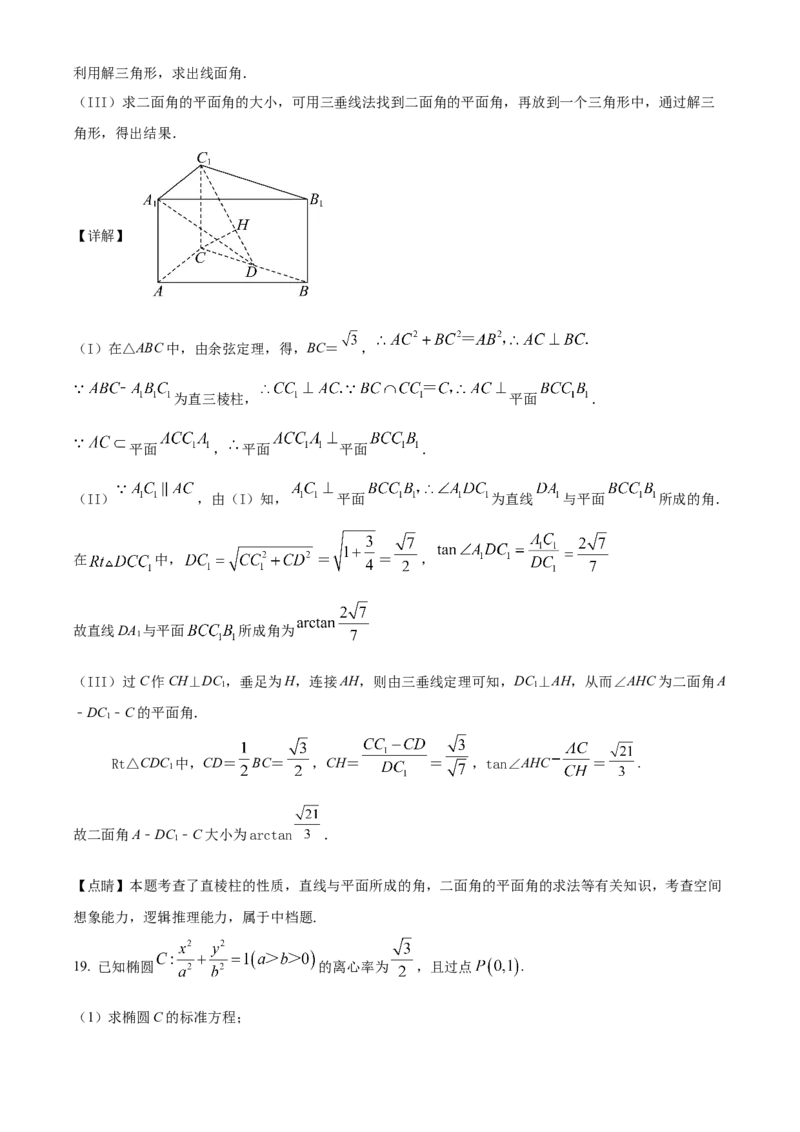
(III)过C作CH⊥DC ,垂足为H,连接AH,则由三垂线定理可知,DC ⊥AH,从而∠AHC为二面角A
1 1
﹣DC ﹣C的平面角.
1
Rt△CDC 中,CD= BC= ,CH= = ,tan∠AHC = .
在1
故二面角A﹣DC ﹣C大小为arctan .
1
【点睛】本题考查了直棱柱的性质,直线与平面所成的角,二面角的平面角的求法等有关知识,考查空间
想象能力,逻辑推理能力,属于中档题.
19. 已知椭圆 的离心率为 ,且过点 .
(1)求椭圆C的标准方程;(2)过定点 的直线 与椭圆C相交于A、B两点,已知点 ,设直线 、 的斜率分
别为 、 ,判断 是否为定值?若是,求出此定值;若不是,说明理由.
【答案】(1) ;(2)是, =1.
【解析】
分析】(1)根据 和过点 求解;
【
(2)(i)若 的斜率不存在,易知 的值,(ii)若 的斜率存在,设 的方程为:
,与椭圆方程联立,由 ,结合韦达定理求解;另解:当直线AB的斜率
不为0时,可设直线AB为: ,解法同上.
详解】(1)∵ ,
【
且过点 , ,
又 ,
解得 ,
∴椭圆 的标准方程 .
(2)(i)若 的斜率不存在,则 , ,
此时 ,(ii)若 的斜率存在,设 , ,设 的方程为: ,
,
由韦达定理得: , ,
,
∴
所以: =1.
另解:(2)当直线AB的斜率为0时, ,
直线AB的斜率不为0时,设直线AB为: ,设 则:
,
,
则: ,
,
所以: =1.
【点睛】方法点睛:求定值问题常见的方法有两种:①从特殊入手,求出定值,再证明这个值与变量无关.②直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.