文档内容
泸州市龙马潭区高 2023 级高二上期半期考试
数学试题
注意事项:
1.答卷前考生务必把自己的姓名、准考证号填写在答题卡上.
2.回答选择题时用2B铅笔将答题卡上对应题目的答案标号涂黑;回答非选择题时,用0.5毫
米黑色墨迹签字笔将答案写在答题卡上,写在本试卷上无效.
3.试卷满分150分,考试时间150分钟,考试结束后将本试卷和答题卡一并交回.
第I卷(选择题)
一、单选题(共40分)
1. 直线 的倾斜角是( )
A. B. C. D.
的
2. 已知实数 , 满足 ,则下列不等式恒成立 是( )
A. B. C. D.
3. 直线 : 和 : 垂直,则实数
A. -1 B. 1 C. -1或1 D. 3
4. ,“直线 和直线 平行”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
5. 已知ΔABC的内角 所对的边分别为 ,若 ,
,则 ( )
A. B. C. D.6. 若 , 满足约束条件 ,则 的最小值为( )
A. -1 B. 0 C. D. 1
为
7. 设k 实数,直线 与圆 交点个数为( )
A. 0 B. 1 C. 2 D. 无法确定
8. 已知直线 过圆 的圆心,且与直线 垂直,则 的方程是( ).
A. B. C. D.
二、多选题(共18分)
9. 已知椭圆 的左、右焦点分别为 ,点 在 上,且 的最大值为3,
最小值为1,则( )
A. 椭圆 的离心率为
B. 的周长为6
C. 若 ,则 的面积为3
D. 若 ,则
10. 已知正方体 的棱长为4,点 为平面 内一动点,则下列说法正确的是(
)
的
A. 若点 在棱 上运动,则 最小值为
B. 若点 是棱 的中点,则平面 截正方体所得截面的周长为
C. 若点 满足 ,则动点 的轨迹是一条直线D. 若点 在直线 上运动,则 到直线 的最小距离为
11. 已知椭圆 的离心率为 ,双曲线 的离心率为 ,
两曲线有公共焦点 是椭圆与双曲线的一个公共点, ,以下结论正确的是( )
A.
B.
C.
D. 若 ,则
三、填空题(共15分)
12. 点 到直线l: 的距离是_______.
13. 正四棱锥 中,底面边长为 ,二面角 为 ,则该四棱锥的高等于
____________.
的
14. 在平面直角坐标系 中,圆 经过点 ,则圆 上 点到原点的距离的最大值
为___________.
四、解答题(共77分)
15. 根据下列给定的条件,判断直线 与直线 是否平行.
(1) 的倾斜角为60°, 经过点 , ;
(2) 平行于y轴, 经过点 , .
16. 为创建全国文明城市,宁德市进行“礼让斑马线”交通专项整治活动,按交通法规定:机动车行经人
行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行.下表是2020年宁德市某一主干路口
监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为,其中违章情况统计数据如下表:月份 1 2 3 4 5
违章驾驶员人数 100 85 80 70 65
(1)请利用所给数据求违章人数y与月份x之间的回归直线方程 ;
的
(2)预测该路口2020年9月份 不“礼让斑马线”违章驾驶员人数;并估计该路口经过几个月后
“不礼让”的不文明行为可以消失.
参考公式: , ,参考数据: .
17. 已知双曲线C: 经过点 ,其中一条渐近线为 ,O为坐标
原点.
(1)求C的标准方程;
(2)过C的右焦点F,且在 轴上的截距为 的直线 ,交 于P,Q两点,求 的值.
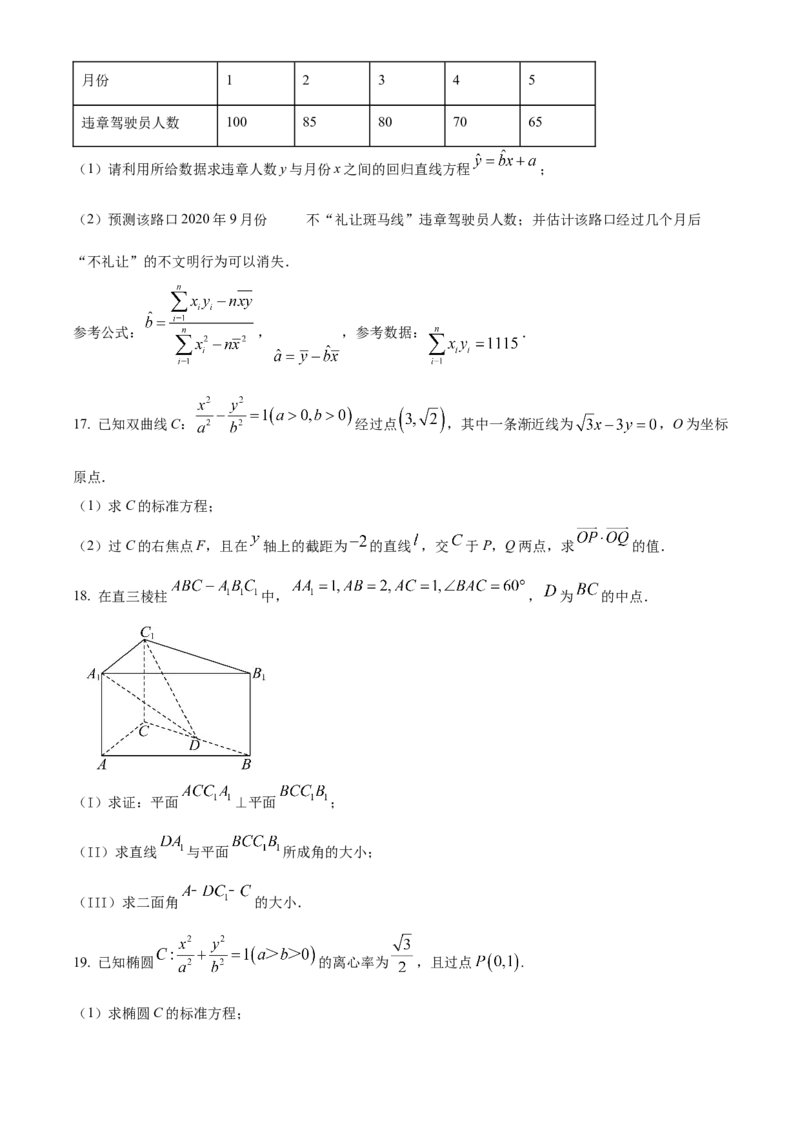
18. 在直三棱柱 中, , 为 的中点.
(I)求证:平面 ⊥平面 ;
(II)求直线 与平面 所成角的大小;
(III)求二面角 的大小.
19. 已知椭圆 的离心率为 ,且过点 .
(1)求椭圆C的标准方程;(2)过定点 的直线 与椭圆C相交于A、B两点,已知点 ,设直线 、 的斜率分
别为 、 ,判断 是否为定值?若是,求出此定值;若不是,说明理由.