文档内容
昆明一中 2024 届高三第 9 次联考
数学参考答案
命题、审题组教师 杨昆华 彭力 李文清 李春宣 丁茵 王在方 张远雄 李露 陈泳序 杨耕耘
一、选择题
题号 1 2 3 4 5 6 7 8
答案 A C D B C C B C
1.解析:因为 ,所以 ,选A.
2.解析:因为 ,所以 ,所以 ,选C.
3.解析:由题意可知,点 的坐标为 ,设点 , , 的坐标分别为 , , ,
又 为△ 的重心,则 ,即 ,所以由抛物线的定义可知
,选D.
4.解析:因为 ,所以 点到圆心的距离恒为 ,所以点 的轨迹方程是以 为圆心,
为半径的圆,即 ,选B.
5.解析:由题意可知, ,即 ,所以A 正确;乙组样本数据方差为 ,所以B 正
确;设甲组样本数据的中位数为 ,则乙组样本数据的中位数为 ,所以两组样本数据的样本中位
数 不 一 定 相 同 , 故 C 错 误 ; 甲 组 数 据 的 极 差 为 , 则 乙 组 数 据 的 极 差 为
,所以两组样本数据的样本极差不同,故D正确,选C.
6.解析:若存在 ,使得 ,等价于函数 在 不是单调函数,
,若函数 为单调递增函数,则 恒成立,即 ,
在 恒成立,则 ;同理,若函数 为单调递减函数,则 恒成
立,得 ,即若函数 在 不单调,则 ,选C.
第 1 页 (共 8 页)
学科网(北京)股份有限公司7.解析:若函数 有“和谐区间”,所以 在 上单调递增,且 在定义域内
有两个不等的实数根, ,即 ,又 在区间 单调递减,在区间
单调递增,且 ,所以 ,又因为 与直线 在 有两个交点,
,所以 ,得 ,所以正整数 的最小值为 , ,即 , ,此时,
实数 的取值范围是 ,选B.
8.解析:设第 个正三角形的内切圆半径为 ,第 个正三角形的边长为 ,可知 ,又半径
为 的圆内接三角形的边长 满足 ,可得 ,即从第二个正三角形开始,每个
正三角形的边长是前一个的 ,每个正三角形的内切圆半径也是前一个正三角形内切圆半径的 ,又
,所以数列 是以 为首项, 为公比的等比数列,所以 ,则
,设前 个内切圆的面积和为 ,
则 ,选C.
二、多选题
题号 9 10 11
第 2 页 (共 8 页)
学科网(北京)股份有限公司答案 BCD BD ABD
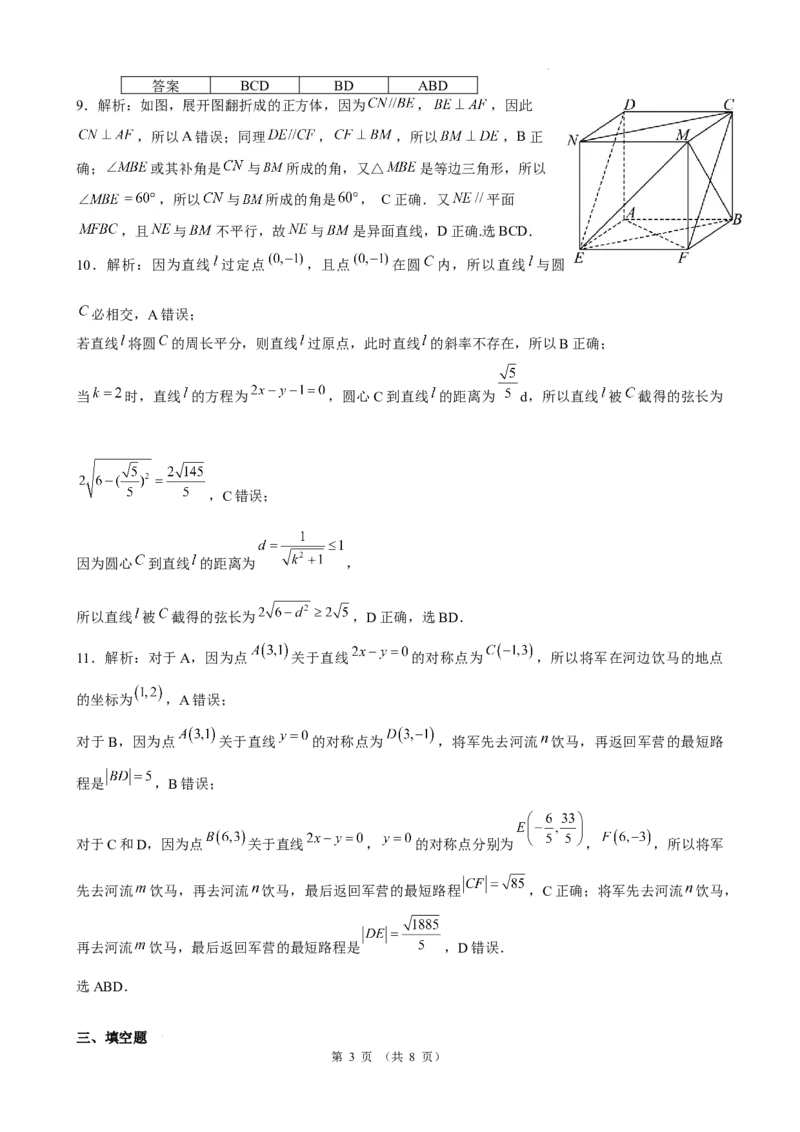
9.解析:如图,展开图翻折成的正方体,因为 , ,因此
,所以A错误;同理 , ,所以 ,B正
确; 或其补角是 与 所成的角,又△ 是等边三角形,所以
,所以 与 所成的角是 , C正确.又 平面
,且 与 不平行,故 与 是异面直线,D正确.选BCD.
10.解析:因为直线 过定点 ,且点 在圆 内,所以直线 与圆
必相交,A错误;
若直线 将圆 的周长平分,则直线 过原点,此时直线 的斜率不存在,所以B正确;
当 时,直线 的方程为 ,圆心C到直线 的距离为 d,所以直线 被 截得的弦长为
,C错误;
因为圆心 到直线 的距离为 ,
所以直线 被 截得的弦长为 ,D正确,选BD.
11.解析:对于A,因为点 关于直线 的对称点为 ,所以将军在河边饮马的地点
的坐标为 ,A错误;
对于B,因为点 关于直线 的对称点为 ,将军先去河流 饮马,再返回军营的最短路
程是 ,B错误;
对于C和D,因为点 关于直线 , 的对称点分别为 , ,所以将军
先去河流 饮马,再去河流 饮马,最后返回军营的最短路程 ,C正确;将军先去河流 饮马,
再去河流 饮马,最后返回军营的最短路程是 ,D错误.
选ABD.
三、填空题
第 3 页 (共 8 页)
学科网(北京)股份有限公司12 . 解 析 : 由 题 意 , , , 且 , 则 , , 则
.
13.解析:由题意知双曲线的渐近线方程为 ,因为 分别为直线 与双曲线 的两条渐近
线的交点,所以不妨设 ,所以 ,因为
(当且仅当 时等号成立),所以 ,所以 的焦距的最小值为 .
14.解析: 人乘坐的所有情况有 种,两个小孩单独乘坐一辆车的情况有
种,由题意知两个小孩不能单独乘坐一辆车,则不同的乘车方式的种数为 种.
四、解答题
15.解:(1)如图,取 中点O,连接 , ,因为△ 是等边三角形,所以 ,
又 ,所以 ,所以 平面 ,所以 ,
又 ,所以 . ………5分
(2)在平面 中,作 ,垂足为D,
由(1)知 平面 ,所以 ,所以 平面 ,如图建立空间直角坐标系 ,
因为三棱柱 的体积为3,所以 ,故 ,
则 , , , ,
z
C
1
所以 , ,
A
1 B
1
设平面 的法向量为 ,
C
O
D
x A B y
第 4 页 (共 8 页)
学科网(北京)股份有限公司则 ,所以 ,
设平面 的一个法向量为 ,
因为二面角 的余弦值为 ,
故 ,化简得: ,即
可得 ,此时 , ,所以 ,
所以直线 与平面 所成角的正弦值为 ,
可得 ,此时, , ,所以 ,
所以直线 与平面 所成角的正弦值为 . ………13分
16.解:(1)由 得: ,又因为 ,所以 ,
所以 ,
又因为 ,所以 . ………5分
(2)在△ 中,由 得: ,由正弦定理 ,得: ,
解得: ,由 ,得 , 所以 ,
因为在△ 中, ,所以
,
第 5 页 (共 8 页)
学科网(北京)股份有限公司所以 . ……… 10分
17.解:(1)依题意随机变量 服从超几何分布,且 .
所以 . ………5分
(2)当 时, ;
当 时, .
令 ,则
.
由 解得 .
所以 时, ;当 时, .
从而当 或 时, 最大,所以 的估计值为 或 . ………15分
18.解:(1)由题意知, , ,
所以 , ,所以 ,
所以 ,所以 . ………5分
的坐标为 ,原点坐标为 ,因为 , ,所以 ,因
(2)设
为 , ,所以 为线段 的中点,所以在△ 中, 是中位线,所以点 的轨
迹 的方程 ………10分
(3)假设存在点 ,使得△ 的面积为 ,则 ,所以 ,
,所以 ,所以
因为
第 6 页 (共 8 页)
学科网(北京)股份有限公司又因为 , ,所以 ,
又因为 ,所以 ,
又因为 ,
所以 ,所以 ………17分
19.解:(1)当 时, , 的定义域为 ,
,
当 时, ,当 时, ,
故 在 内单调递增,在 单调递减,
即 的单调增区间为 ,单调减区间为 ; ……………7分
(2)证明:因为曲线 与直线 有且仅有两个交点,
所以方程 有且仅有两个不同的实数根,
即方程 ,即 有且仅有两个不同的实数根,
构造 ,则 ,
当 时, ,当 时, ,
故 在 内单调递增,在 单调递减,
所以 ,又 ,当 时,则 ,
第 7 页 (共 8 页)
学科网(北京)股份有限公司因为 ,故 有且仅有两个不同的实数根的充要条件为 ,
即 ,故实数 的取值范围为 . ………17分
第 8 页 (共 8 页)
学科网(北京)股份有限公司