数学答案（一中）-2_2024年5月_01按日期_1号_2024届湖南省长沙市第一中学高考适应性演练(二）_2024届湖南省长沙市第一中学高考适应性演练(二）数学试卷

长沙市一中 2024 届高考适应性演练（二） 数学参考答案 一、选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一 项是符合题目要求的） 1．D 【解析】因为log x1log 2，所以0 x2， 2 2     即M  x log x1  x 0 x 2 ， 2 1    1 因为2x10，解得x ，所以N  x 2x10  x x ， 2  2  1 所以，M N  x 0 x .  2 故选：D 2．C 【解析】由 z 1可设：zcosisin， z34icos3sin4i，  z34i  cos32sin42  cos2sin26cos8sin25 3 4  2610cos（其中cos ,sin ）， 5 5 3 4 当cos1时，即z  i时， 5 5 z34i  2610 6. max 故选：C. 3．C  π 5 【解析】因为sin  ，  3 5 2π   2π    π  所以cos 2cos2 cos 2   3   3    3 2  π  5 3 12sin2  12     .  3  5  5 故选：C 4．C 数学（一中）答案 （第 1 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}【解析】由题意得 x2x2 4   x2x  2 4 ，   其展开式为T Ck x2x 4k2k， k1 4 则对于 x2x 4k的展开式为T Cr  x24krxr 1r Cr x82kr， r1 4k 4k 0r4k， 令82kr1，则当k 3，r 1时符合题意， 此时系数为23 C3·11 C1 32，故C正确. 4 1 故选：C. 5．C 【解析】由x12  y2 4可知圆心C(1,0)，半径为2， 因为四边形PMCN为正方形，且边长为圆C的半径2，所以PC2 2， 所以直线l：x ym0上有且只有一个点P，使得PC2 2，即PCl， 所以圆心C到直线l的距离为2 2， |10m| 所以 2 2，解得m3或m5（舍）. 11 故选：C 6．C x x 【解析】∵f(x)＝log ·log ＝(log x－1)·(log x－3)＝(log x)2－4log x＋3， 2 2 2 2 2 2 2 8 由f(x )＝f(x )，∴log x ＋log x ＝4， 1 2 2 1 2 2 1 9 9 3 3 即x x ＝16，∴ ＋ ≥2 ＝2× ＝ ， 1 2 x x x x 4 2 1 2 1 2 1 9 当且仅当 ＝ ， x x 1 2 4 即x ＝ ，x ＝12时等号成立．故选C． 1 2 3 7．D 1 【解析】三队中选一队与丙比赛，丙输，C1 ，例如是丙甲， 3 3 若丙与乙、丁的两场比赛一赢一平，则丙只得4分， 这时，甲乙、甲丁两场比赛中甲只能输，否则甲的分数不小于4分，不合题意， 在甲输的情况下，乙、丁已有3分， 那个它们之间的比赛无论什么情况， 乙、丁中有一人得分不小于4分，不合题意. 1 若丙全赢（概率是( )2）时，丙得6分，其他3人分数最高为5分， 3 这时甲乙，甲丁两场比赛中甲不能赢，否则甲的分数不小于6分， 1 （1）若甲乙，甲丁两场比赛中甲一平一输，则一平一输的概率是C1( )2， 2 3 数学（一中）答案 （第 2 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}2 如平乙，输丁，则乙丁比赛时，丁不能赢，概率是 ， 3 1 （2）若甲乙，甲丁两场比赛中甲两场均平，概率是( )2， 3 乙丁这场比赛无论结论如何均符合题意， 1 （3）若甲乙，甲丁两场比赛中甲都输，概率是( )2， 3 1 乙丁这场比赛只能平，概率是 . 3 1 1 1 2 1 1 1 8 综上，概率为C1 ( )2[C1( )2 ( )2( )2 ] ，D正确． 3 3 3 2 3 3 3 3 3 35 故选：D. 8．D 【解析】在长方体ABCDABCD 中，由于DA平面AABB ，CB平面AABB ， 1 1 1 1 1 1 1 1 AD BE 在Rt△PAD和RtPBC中，tanAPD ，tanEPB ， AP PB 1 1 1 tanAPD4tanEPB，BE BC AD，PA PB， 2 2 2 在平面ABBA ，以A为坐标原点，以AB,AA 为x,y轴的正方向，建立平面直角坐标系， 1 1 1 设P(x,y),则A0,0,B(4,0)， 1 1 则由PA PB可得 x2 y2  x42 y2 ， 2 2 2  4 64 化简可得 x  y2 ，  3 9 由于x0,y0，  4  8 故P的轨迹表示圆心在 ,0，半径为r 的圆在第一象限的弧长，  3  3  4 3 由于Q0, ,    3  π π π 8 8π 故QMA ,因此轨迹为QMA 所对的弧长，故长度为   ， 3 3 3 3 9 故选：D 数学（一中）答案 （第 3 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}二、选择题（本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合 题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分） 9．ABD     【解析】由 f x 为奇函数，即函数 f(x)的图象关于 0,0 对称， 又 f  1x  f  1x  ，则 f  x  的图象关于x1对称， 所以 f(x2) f(x)f(x)， 则 f(4x)f(x2) f(x)，  f  x  为周期函数且周期为T  4，B对． 所以 f  3  f 1 1，A对． 而 f(4x) f(x)f(x)，C错． 由上可知 f  2 f  0 0， f  4  f  0 0， 所以 f  1  f  2  f  3  f  4 f 1 0100， 18 则  f(k) f(1) f(2)1，D对． k1 故选：ABD． 10．BC S 【解析】由已知得，a  ， 1 3 S S 不难得到，nN*，a  n ，所以A错误. n1 3 S S S S 走n段距离后，由a  n 得a  n1 n 2 ， n1 3 n 3 2 两式相减化简得a  a  n2 ， n1 3 n S 2S 1 2 当n 1时，a  ,a    a 也符合，所以B正确. 1 3 2 3 3 3 1 数学（一中）答案 （第 4 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}由a  2 a 可知  a  是公比为 2 ，首项为 S 的等比数列， n1 3 n n 3 3 n 2 1    n S 3 2 S   S 1   S ，所以C正确，D错误. n 3 1 2  3  3 故选：BC. 11．BD 【解析】对于A：  p p 由已知设过点F  0, 的直线方程为 y kx ,k 0，A  x ,y  ,B  x ,y ，  2  2 1 1 2 2  p 联立方程   y kx 2 ，消去x得 y2   2k2 1  py p2 0，  x2 2py 4 p2 可得 y y  ， 1 2 4  p y   2   2 2 又因为 AF 2 BF 4，所以 ， p  y   4  1 2  p p p2 8 则 y y  2 4   ，解得 p  , 1 2  2 2 4 3 16 4 所以抛物线方程为x2  y，准线方程为 y  ，A错误； 3 3 16 3 3 对于B：抛物线E:x2  y，即 y  x2， y x， 3 16 8 3 3 易得k  x ,k  x ， NA 8 1 NB 8 2 9 9 9 64 1 64 所以k k  x x  4p2y y  4   1， NA NB 64 1 2 64 1 2 64 9 4 9 故直线NA,NB垂直，所以点N 在以AB为直径的圆上，B正确； 16 4 对于C：由A项知，抛物线E:x2  y，直线l的方程为 y kx ,k 0， 3 3 A  x ,y  ,B  x ,y ， 1 1 2 2 数学（一中）答案 （第 5 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#} 4 y kx   3 8  2k2 1  16 联立方程 ，消去x得 y2  y  0 ， 16  x2  y 3 9  3 16 8  2k2 1  可得 y y  ， y  y  ， 1 2 9 1 2 3 p p 8 8  2k2 1  | AF ||BF |  y   y  p y  y   6 ， 2 1 2 2 1 2 3 3 2 解得k  ， 4 10 所以 y  y  ， 1 2 3 4 4 10 8 y  y   1 3 2 3 3 3 4 2 所以x x     ， 1 2 k k 2 3 4 x x 2 2 y y 5 2 2 5 所以 1 2  , 1 2  ，即M   ,   ， 2 3 2 3  3 3  2 2  2 5 2 33 所以 OM          ，C错误；  3  3 3 8 8  2k2 1  2 对于D：由C选项知 | AF ||BF |  6 ，k  ， 3 3 4 因为直线l垂直于直线m，   1 2    4  2  82    1 82    1 所以 8   k   8   2  |CF ||DF |    48 3 3 3 3 则 AB CD  288，D正确. 故选：BD. 三、填空题（本题共3小题，每小题5分，共15分） 12．－540 n  1 【解析】由二项式 3x  的展开式中所有二项式系数之和为64，  x － 1 k 得2n＝64，即n＝6，所以T k＋1 ＝Ck 6 (3x)6－k· x ＝Ck 6 36－k·(－1)kx6－2k. 令6－2k＝0，得k＝3， 所以二项式的展开式中常数项为C3×36－3×(－1)3＝－540. 6 数学（一中）答案 （第 6 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}13．0.3；0.98 【解析】因为 f cWk，两边取对数可得ln f lncklnW ， 又x lnW ，y ln f ， i i i i   依题意回归直线方程ybx7.4必过样本中心点 x,y ， 所以 58b7.4 ，解得 b 0.3 ，所以k 0.3， 8  2 8  2  y y  y y i i i i 0.28 又R2 1 i1 1 i1 1 0.98.  8  y  y 2  8 y2 8y 2 214852 i i i1 i1 故答案为：0.3；0.98. 14． 2π 【解析】如图：取CC ,DD ,CD的中点E,F,G ,连接AC,AG,AE,AF,FG,EG ， 1 1 结合题意：易得ACD为等边三角形， 因为G为CD的中点，所以AGCD 因为在直四棱柱ABCDABCD 中有CC 面ABCD,且AG面ABCD， 1 1 1 1 1 所以AGCC ,又因为CC CD C ,且CC ,CD 面CC DD 1 1 1 1 1 所以AG 面CC DD ，结合球的性质可知G为该截面圆的圆心， 1 1 因为直四棱柱ABCDABCD 的所有棱长均为4，ABC 60， 1 1 1 1 所以EGF 90 ,AG 2 3, AE  AF  2 5 ,EG2 2, 故以A为球心，2 5为半径的球面与侧面CDDC 的交线为：以G为圆心, 2 2为半 1 1 径的圆所成的圆弧EF. 1 1 所以E  F  2πr  2π2 2 2π. 4 4 故答案为: 2π. 数学（一中）答案 （第 7 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}四、解答题（本题共6小题，共70分） 15．解：（1） f x x2axa1， f23a3 由已知 f 26， ∴3a36得a3 31 又 f 2  3 ∴曲线 f x在点  2,f 2 处的切线方程为y 31 6x2 3 化简得：18x3y5 0 1 a （2） f x x3 x2 a1x1定义域为R， 3 2 f x  xa1  x1 ，令 fx0得x1a或x=1 ①当1a1即a2时， 令 f¢(x)>0得x1或x1a，令 fx0得1a x1， 故 f x在1a,1单调递减，在 ,1a  ，1,上单调递增； ②当1a1即a2时， fxx12 0恒成立， 故 f x在R上单调递增； ③当1a1即a2时， 令 f¢(x)>0得x1a或x1，令 fx0得1 x1a， f x在1,1a上单调递减，在,1，1a,上单调递增； 综上，当a2时， f x在1a,1单调递减，在 ,1a  ，1,上单调递增； 当a2时， f x在R上单调递增； 当a2时， f x在1,1a上单调递减，在,1，1a,上单调递增. 16．解：（1）证明：在△ABC中， 1 ∵O为BC中点且AO＝ BC， 2 ∴AB⊥AC. ∵平面ABC⊥平面ACC A 且交线为AC， 1 1 ∴AB⊥平面ACC A ，∴AB⊥CM. 1 1 ∵M，N分别为AA ，BB 的中点， 1 1 ∴MN∥AB.∴CM⊥MN. 在直角△AMC和直角△MA C 中， 1 1 ∵AM＝A M＝8，AC＝A C ＝8， 1 1 1 数学（一中）答案 （第 8 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}∴△AMC≌△A MC ， 1 1 ∴CM＝C M＝ 64＋64＝8 2， 1 ∴CM2＋C M2＝128＋128＝162＝CC2， 1 1 ∴CM⊥C M，MN∩C M＝M. 1 1 ∵MN，C M⊂平面C MN， 1 1 ∴CM⊥平面C MN，C N⊂平面C MN， 1 1 1 ∴CM⊥C N. 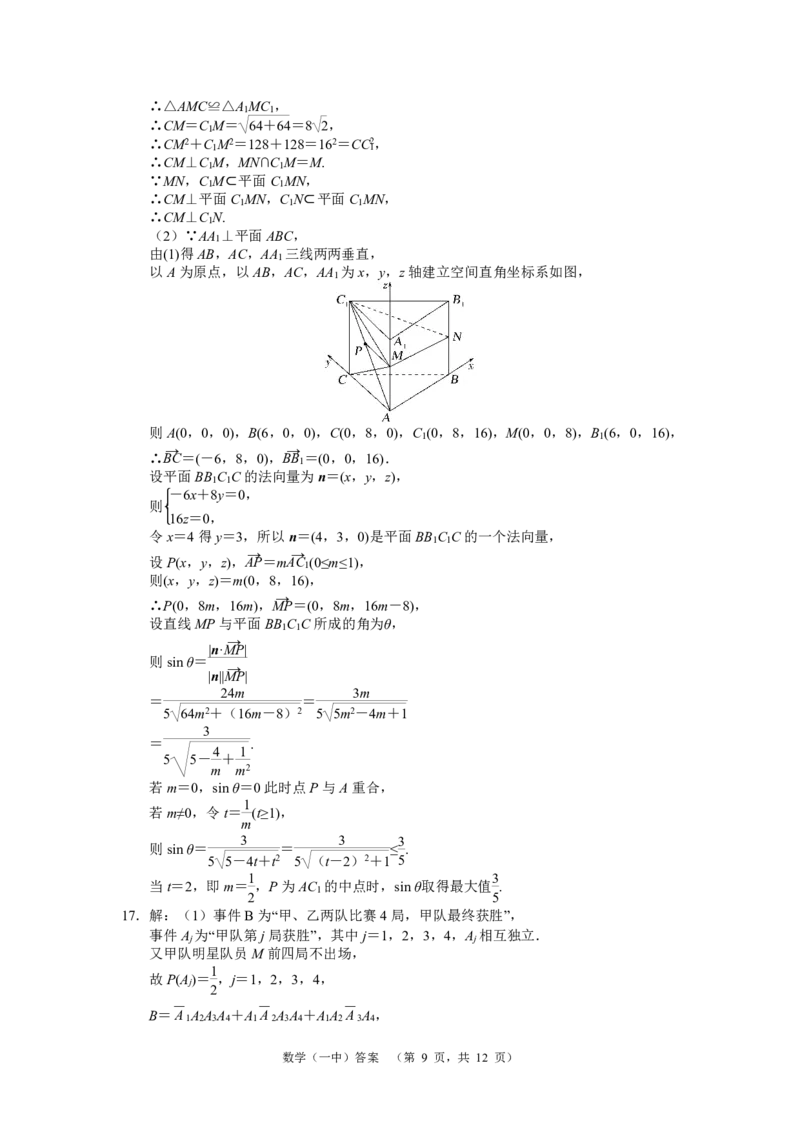1 （2）∵AA ⊥平面ABC， 1 由(1)得AB，AC，AA 三线两两垂直， 1 以A为原点，以AB，AC，AA 为x，y，z轴建立空间直角坐标系如图， 1 则A(0，0，0)，B(6，0，0)，C(0，8，0)，C (0，8，16)，M(0，0，8)，B (6，0，16)， 1 1 → → ∴BC＝(－6，8，0)，BB ＝(0，0，16)． 1 设平面BB C C的法向量为n＝(x，y，z)， 1 1 －6x＋8y＝0， 则 16z＝0， 令x＝4得y＝3，所以n＝(4，3，0)是平面BB C C的一个法向量， 1 1 → → 设P(x，y，z)，AP＝mAC (0≤m≤1)， 1 则(x，y，z)＝m(0，8，16)， → ∴P(0，8m，16m)，MP＝(0，8m，16m－8)， 设直线MP与平面BB C C所成的角为θ， 1 1 → |n·MP| 则sinθ＝ → |n||MP| 24m 3m ＝ ＝ 5 64m2＋（16m－8）2 5 5m2－4m＋1 3 ＝ . 4 1 5 5－ ＋ m m2 若m＝0，sinθ＝0此时点P与A重合， 1 若m≠0，令t＝ (t≥1)， m 3 3 3 则sinθ＝ ＝ ≤ . 5 5－4t＋t2 5 （t－2）2＋1 5 1 3 当t＝2，即m＝ ，P为AC 的中点时，sinθ取得最大值 . 1 2 5 17．解：（1）事件B为“甲、乙两队比赛4局，甲队最终获胜”， 事件A 为“甲队第j局获胜”，其中j＝1，2，3，4，A 相互独立． j j 又甲队明星队员M前四局不出场， 1 故P(A)＝ ，j＝1，2，3，4， j 2 － － － B＝A A A A ＋A A A A ＋A A A A ， 1 2 3 4 1 2 3 4 1 2 3 4 数学（一中）答案 （第 9 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}1 4 3 所以P(B)＝C1 3 2 ＝ . 16 （2）设事件C为“甲队3局获得最终胜利”，事件D为“前3局甲队明星队员M上场比 赛”， 因为每名队员上场顺序随机， C2A3 3 － 3 2 所以P(D)＝ 4 3＝ ，P(D)＝1－ ＝ ， A3 5 5 5 5 1 2 1 3 3 3 － 1 P(C|D)＝ 2 × ＝ ，P(C|D)＝ 2 ＝ ， 4 16 8 － － 3 3 2 1 13 由全概率公式，知P(C)＝P(D)P(C|D)＋P(D)P(C|D)＝ × ＋ × ＝ . 5 16 5 8 80 3 3 × P（CD） P（D）P（C|D） 5 16 9 （3）由（2），得P(D|C)＝ ＝ ＝ ＝ . P（C） P（C） 13 13 80 18．解：（1） F，F 为椭圆C的两焦点，且 P ，Q 为椭圆上的点， 1 2 2 PF PF Q F Q F 2a，从而△PQ F的周长为4a． 1 2 2 1 2 2 2 1 由题意，得4a4 2，即△PFQ 的周长为4 2. 1 2 （2）由题意可设过 PQ 的直线方程为xmy1，P(x ,y ),Q (x ,y ),(x 0,y 0) 2 0 0 2 2 2 0 0 xmy1 联立  ，消去x得(m22)y22my10， x22y2 2 2m 1 则y y  ,y y  ， 0 2 m22 0 2 m22 2  2m  4 8 8 所以 | y y |      ， 0 2 m22 m22 m22 (m22)2 1 1 令t (0t ）， m22 2 则| y y | 8(tt2)  2 （当 t  1 时等号成立，即m0时） 0 2 2 1 1 所以S  |FF ||y y | 2|y y ||y y | 2, △PF1Q2 2 1 2 0 2 2 0 2 0 2 故△PFQ 面积的取值范围为 0, 2. 1 2  （3）设Q(x,y )，直线 FP 的方程为： y y 0 (x1) ， 1 1 1 1 x 1 0 将其代入椭圆的方程可得x2  y 0 2 (x1)2 1 ， 2 (x 1)2 0 整理可得 (2x 3)x24y2x3x24x 0 ， 0 0 0 0 则 3x2 4x ，得 3x 4 ， y 3x 4 y ， x x  0 0 x  0 y  0 ( 0 1) 0 0 1 2x 3 1 2x 3 1 x 1 2x 3 2x 3 0 0 0 0 0 数学（一中）答案 （第 10 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}故 3x 4 y ． Q( 0 , 0 ) 1 2x 3 2x 3 0 0 y 当x 1时，直线F P的方程为： y 0 (x1) ， 0 2 x 1 0 将其代入椭圆方程并整理可得 (2x 3)x24y2x3x24x 0 ， 0 0 0 0 同理，可得 3x 4 y ， Q ( 0 , 0 ) 2 2x 3 2x 3 0 0 1 1 因为S  4 2r,S  4 2r ， △PF1Q2 2 1 △PF2Q1 2 2 1 1 所以 r r  S △PF1Q2  S △PF2Q1  S △F1F2Q2  S △F1F2Q1  2 2(y 2 ) 2 2(y 1 ) 1 2 2 2 2 2 2 2 2 2 y y 2 y y  2 2x y 2 2 2 2 1 ，  1 2   0  0  0 0    2 2 4  2x 0 3 2x 0 3 x 0 218 y 0 2 x 0  18y 0 2 x 0 1  8 y 0 3 y x y x 0 0 0 0 3 5 10 当且仅当 x  ,y  时，等号成立. 0 5 0 10 2 2 2 若PF x轴时，易知P(1, )，y  ， y  ， 2 2 1 10 2 2 y  y 2 4 2 1 此时 r r  1 2    ， 1 2 2 2 4 10 5 综上，r r 的最大值为1 . 1 2 3 19．解：（1）由题设知当n3时，a a ,a a ，故n3是数列A的一个“D时刻”， 1 3 2 3 同理当n5时，都有a a i1,2,3,4，即n5也是数列A的一个“D时刻”， i 5 综上，DA3,5. （2）解法一： 由cardD,A4，易知a 5或a 6 1 1 ①当a 5时，4,3,2,1必须从左往右排列，6可以是a i2,3,4,5,6中任一个，共有5 1 i 种情况 ②当a 6时，若DA中的四个元素是由集合A中的元素4,3,2,1或5,3,2,1或5,4,2,1 1 或5,4,3,1引起的 1.若由4,3,2,1引起，即4，3，2，1从左往右排列，则5必须排在4的后面，共4种； 2.若由5,3,2,1引起，即5，3，2，1从左往右排列，则4必须排在3的后面，共3种 3.若由5,4,2,1引起，即5,4,2,1从左往右排列，则3必须排在2的后面，共2种； 4.若由5,4,3,1引起，即5,4,3,1从左往右排列，则2必须排在1的后面，共1种 数学（一中）答案 （第 11 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}综上，符合cardD,A4的数列A有15种 解法二： 因为数列A:a ,a ,,a 1,2,3,4,5,6， 1 2 6 由题意可知DA中的四个元素为2,3,4,5,6中的四个，共有5种情况： ①当DA3,4,5,6时，数列A5,6,4,3,2,1共有1种情况； ②当DA2,4,5,6时，数列A6,4,5,3,2,1,5,4,6,3,2,1共有2种情况； ③当DA2,3,5,6时，数列A6,5,3,4,2,1,6,4,3,5,2,1,5,4,3,6,2,1共有3种情 况； ④当DA2,3,4,6时， 数列A6,5,4,2,3,1,6,5,3,2,4,1,6,4,3,2,5,1, 5,4, 3,2,6,1共有4种情况； ⑤当DA2,3,4,5时， 数列A6,5,4,3,1,2,6,5,4,2,1,3,6,5,3,2,1,4, 6,4, 3,2,1,5，5,4,3,2,1,6共有 5 种 情况； 综上，符合cardD,A4的数列A有15种. （3）①若cardD,A0，由a a ， 1 N 所以a a 0，即cardD,Aa a 成立； 1 N 1 N ②若cardD,Amm1， 不妨设DAi,i ,i ,,i ,i i i i 且2i  Nj1,2,,m 1 2 3 m 1 2 3 m j 从而a a a a 1;a a a a 1;;a a a a 1 i1 1 i1 i1 1 i2 i1 i2 i2 1 im im1 im im 1 由累加法知：a a m im 1 又a a a a m，即ma a ； N 1 im 1 1 N 综上，cardD,Aa a ，证毕. 1 N 数学（一中）答案 （第 12 页，共 12 页） {#{QQABaYiAogCAAJIAABhCEQVQCgMQkAAAAIoGgAAAsAAACQFABCA=}#}