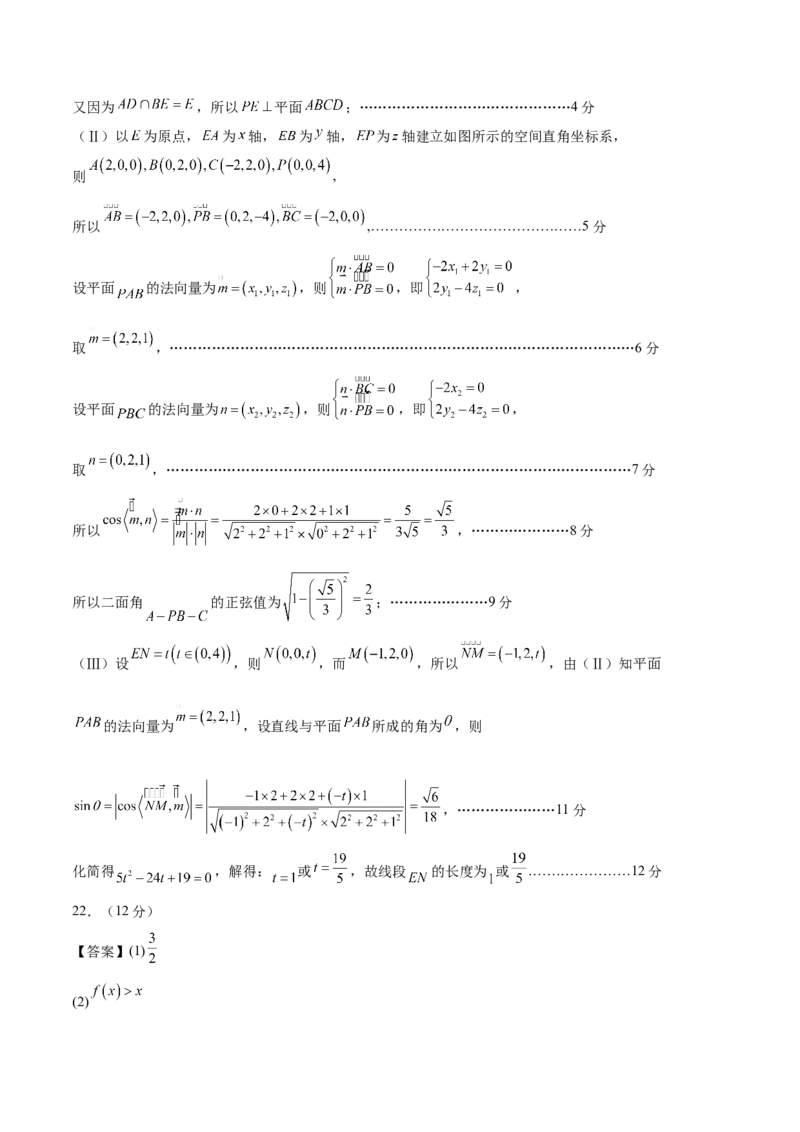文档内容
2024 年高考数学第一次模拟考试
数学(新高考 I 卷)·参考答案
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合要求的。
1 2 3 4 5 6 7 8
D A C B A D D A
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符
合题目的要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9 10 11 12
BCD ABD ACD AC
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13. 14. 15. 16. 2
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(10分)
【答案】(1) ;(2) .
【详解】(1)由已知及正弦定理得 ,…………………………1分
则 ,………………………3分
在 中 ,故 , ……………………………………………4分
又 ,故 . ……………………………………………………………………………5分
(2)由 ,得 , ……………………………………………6分由题意 ,则 ,……………………7分
即 ,解得 ,……………………………………………9分
故 的面积为 . ……………………………………………10分
18.(12分)
【答案】(1)证明见解析 (2)
【详解】(1)令 ,得 ,则 .……………………………………………1分
因为 ①,所以 ②.…………………………… ………2分
①-②得 ,即 . …………………………4分
因为 ,所以数列 为常数列.……………………………………………5分
(2)由(1)可得 ,所以 是公差为1的等差数列,
所以 .……………………………………………………………………………………………7分
因为 , ………………………………………………………………………8分
所以 ③,
④.………………………………………………………………………9分
③-④得,…………………………………………………………………11分
所以 . …………………………………………………………………12分
19.(12分)
【答案】(1) (2)应选择先回答甲类问题
【详解】(1)设 “张某选择甲类问题”, “张某答对所选问题”,
“张某至少答对一道问题”,
“张某选择乙类问题”, “张某未答对所选问题”
“张某一道问题都没答对”
由题意得, ,……………………………………………………………1分
, , , ,…………………………3分
由全概率公式,得
…………………………4分
∴ .……………………………………………………………5分
(2)根据条件可知:若张某先回答甲类问题,
则张某的累计得分X的可能值为0,30,80,
∵张某能正确回答甲类问题的概率为0.9,能正确回答乙类问题的概率为0.7,
∴ ;
;
,……………………………………………7分
则 的分布列为
0 30 80
0.1 0.27 0.63
当张某先回答甲类问题时,累计得分的期望为:,……………………………………………8分
若张某先回答乙类问题,则张某的累计得分 的可能值为 ,
同理可求 ; ;
,……………………………………………………………………10分
则此时累计得分的期望为 ,……………………11分
因为 .
所以,以累计得分多为决策依据,张某应选择先回答甲类问题.……………………12分
20.(12分)
【答案】(1) ,准线方程为
(2)证明见解析
【详解】(1)因为点 在 上,
所以 ,解得 ,…………………………………………………………2分
所以 的方程为 , …………………………………………………………3分
准线方程为 . …………………………………………………………………………4分
(2)易知直线 的斜率存在,设直线 的方程为 ,………………………5分
联立 ,得 ,…………………………………7分
设点 ,则 .…………………………………8分
直线 的方程为 ,令 ,
得 ,所以 ,…………………………………9分同理得 ,…………………………………10分
设以线段 为直径的圆与 轴的交点为 ,
则 ,
因为 ,则 ,
即 ,…………………………………11分
所以 ,解得 或 .
故以线段 为直径的圆经过 轴上的两个定点 和 .…………………………………12分
21.(12分)
【答案】(Ⅰ)证明见解析;(Ⅱ) ;(Ⅲ) 或 .
【详解】
(Ⅰ)连接 ,则 ,因为 ,所以四边形 为平行四边形;所以
,因为 且 为 的中点,所以 ,………2分
所以 ,所以 ,即 ,………3分又因为 ,所以 平面 ;………………………………………4分
(Ⅱ)以 为原点, 为 轴, 为 轴, 为 轴建立如图所示的空间直角坐标系,
则 ,
所以 ,………………………………………5分
设平面 的法向量为 ,则 ,即 ,
取 ,………………………………………………………………………………………6分
设平面 的法向量为 ,则 ,即 ,
取 ,………………………………………………………………………………………7分
所以 ,…………………8分
所以二面角 的正弦值为 ;…………………9分
(Ⅲ)设 ,则 ,而 ,所以 ,由(Ⅱ)知平面
的法向量为 ,设直线与平面 所成的角为 ,则
,…………………11分
化简得 ,解得: 或 ,故线段 的长度为 或 .…………………12分
22.(12分)
【答案】(1)
(2)(3)证明见解析
【详解】(1)解:因为函数 ,可得 ,…………………1分
则 ,……………………………………………………………………………2分
所以曲线 在 处切线的斜率为 .…………………………………………………3分
(2)解:设函数 ,
可得 ,………………………………………4分
当 时, ,则 在 上单调递增,………………………………………5
分
所以 ,从而 ,所以 .…………………………………6分
(3)证明:设函数 ,
当 时, , ,则 恒成立,
则由 ,得 ,……………………………………………………………7分
又 ,所以 ,……………………………………………8分
因为 ,可得 ,
令 ,可得 ,
所以 单调递增,即 在 单调递增,所以 ,
所以 在 上单调递增,又由 ,所以 ,………………………………………………9分
同理得 ,
要证 ,只需证 ,即证 ,
因为 ,所以 ,……………………………………………………………10分
设函数 ,则 ,所以 在 上单调递增,
因为 ,所以 ,所以 ,所以 ,……………………………11分
所以 ,从而得证 .……………………………12分