河北省保定市2024届高三第一次模拟考试数学参考答案_2024年4月_01按日期_11号_2024届河北省保定市高三第一次模拟考试_河北省保定市、邢台市2024年高三第一次模拟考试数学

2024 年高三一模数学试题参考答案
一、选择题：
1．B 2．A 3.D 4.B 5.C 6．A 7.C 8．D
8.【参考解析】因为 ， ，所以 ，

2≤  <   =   = 
设 ，则 ，
' 1−   
2
令   =  ，  则 ≥2  ，  令 =  ，则 ，
' '
所以   >在0 上2<单  调<递  增，在   <0 上单  调>递  减，
2,   ,+∞
因为 ， 4， ，
2
所以  2 =  4 = 2 ， 2 故 ≤ 选   ： < D   ≤    =   
二、选择题：
2≤  <  <  ≤4
9.AC 10.ABD 11．BCD
11.【参考解析】对于A，令 ，则
因为 ，所以 ，则 ，
=  =4 2  4 =2  4 ⋅  0
故A错误；
(4)=−1 −2=−2  0  (0)=1
对于B，令 ，则 ，
则 ，故B正确；
=  ,  =−   (  )+  (−  )=2  (0)  (  )=2  
对于C，令 得， ，
(  )=  (−  )
所以 ， 2
=4,  =0  4 +  0 =2  2 =0
令 得， ，
2 =0
则 的图像关于点 ， 对称，故C正确；
=2+  ,  =2−   (2+  )+  (2−  )=2  (2)  (  )=0
对于D，由 得 ，
(  ) (2 0)
又 ，所以 ，
(2+  )+  (2−  )=0   =−  4− 
则 ， ，
(  )=  (−  )  −  =−  4− 
所以 ，则函数 的周期为 ，
=−  4+   4+  =−  8+ 
又 ， , ， ，
=  8+    8
则 ，
1 +  3 =0  2 =  6 =0  5 +  7 =0  4 =−1  (8)=1
所以 ，
1 +  2 +  3 +⋯+  8 =0
故D正2确024，故选：BCD.
  =1  (  )=253×0=0
三、填空题：
12． 13. 14．
2
1
>1
14.【  参考解析】如图所示．由题意2 得球O的球心为底面△BCD的26中心，设正四面体A－BCD的棱长为a，
则球O的半径 ，所以 ，
3  3 
= 3   1 =  = 3
由于OA⊥OB，所以 ，
2
2 3  6 
在Rt△ABO中，过O作AB的垂线OH，
=  − 3 = 3
1
学科网（北京）股份有限公司1 1
则 OH·AB＝ OB·OA，则 ，
2 2
∙   2 
=   = 3
利用勾股定理BH2＋OH2＝OB2，得 ，同理 ，所以 ，
2 
BB 2 AB 1   =3  1  =3   1 = 3
因为 1＝ ， 1＝ ，
AB 3 AB 3
1 26 26
所以 三棱锥 ＝ ，三棱台BCD－BCD的体积 ＝ V ＝
三棱锥  −  1  1  1 27 1 1 1 三棱台 － 27 三棱锥A－BCD 27
所以  三棱锥  −    故答案为：   1  1  1   
三V棱台 A−B1C1D1 1 1
四、V解答−题B1 ：C1D1 本−B题CD =共256 小题，共7276 分。解答应写出文字说明、证明过程或演算步骤。
15.（13分）
aex2xaex2 1 1 aex2 x1  x1  x1  aex21 
解：（1）因为 f x       ，......3分
x2 x x2 x2 x2 x2
1 a1 1
由已知 f 2  ， 即  ， ....................4分
4 4 4
解得a2 ....................5分
 x1  2ex21 
（2）a2则 f x   0，
x2
解得x1或x2ln2 ....................7分
当0 x1时，x10，2ex2 10，则
f
x

0； ....................8分
当1 x2ln2时，x10，2ex2 10，则 f x 0；....................9分
当x2ln2时，x10，2ex2 10，则
f
x

0，....................10分
所以 f

x

的单调递增区间为
 0，1
和
 2ln2，
，....................11分
减区间为
 1，2-ln2
...................12分
2
函数 f  x  的极大值为 f  1  1 ....................13分
e
16.（15分）
解:（1）证明：在 中，由 ， ，
得 ，所以 ，...................3分
△    1   =  1  = 2   1 =2
又因为2 平2 面 2
+  1  =   1   ⊥  1 
所以 ...................4分
⊥   1 
所以 平面 ...................5分
⊥  
所以平面 平面 ...................6分
⊥   1 
（2）解在  三   棱⊥柱   1  中，取 BB 1的中点 ，连接 ，
−  1  1  1    ,  
2在 中，由 ， ，得CDBB ， ，...................7分
1
且△    1 ,得   =  1，  =即∠2   为1二=面2角  的  平=面1角，...................8分
在   =A中  1， AD∠⊥ BB1   ，  解得  −  ，  .1.−..  .1..............9分

△          =   = 3   = 3
BCCB
由（1）知， 平面 ， 1，
以 为原点， A 直 C 线 ⊥ BB1C 分别为 轴，如图建立空间直角坐标系，
，B(0,  2  ,10,)  ，  ,    ，,  , 
(0,=0, 3) ，  1( 2,0,0)
，
  1 ( 2,− 2 0)
,...................11分
1  1=    =(0, 2,0)
设平面 的法向量为 ，
  1=( 2,0,− 3)
则   1  1   =，(  ,  ,  )
  ⋅    1= 2  − 3  =0
令 ，得 ，...................12分
  ⋅  1  1= 2  =0
设直线 与平面 所成的角为 ，
= 3   =( 3,0, 2)
则    1   1  1  ，...................14分
|  ⋅    1| 6 30
=|    ⟨  ,    1⟩|= |  |⋅|    1|= 5⋅2= 10
所以 与平面 所成的角的正弦值为 ....................15分
30
17. （   1 1 5分）   1  1 10
解：（1）每部电影至少有一人去看，五名同学去看三部电影所有可能情况有
C2C2
5 3 A3 C3A3 150种，...................2分
A2 3 5 3
2
只有甲、乙看《热辣滚烫》的共有C2A2 6种，...................4分
3 2
6 1
只有甲、乙去看《热辣滚烫》电影的概率 p   ；...................6分
1 150 25
（2）设去看《热辣滚烫》的人数为，的可能取值为1，2，3
C1(C2C2 C3A2) 70 7
P  1   5 4 2 4 2   ，...................8分
150 150 15
C2C2A2 60 2
P  2   5 3 2   ，...................10分
150 150 5
C3A2 20 2
P  3   5 2   ，...................12分
150 150 15
随机变量的分布列为：
3
学科网（北京）股份有限公司 1 2 3
7 2 2
P
15 5 15
...................13分
7 2 2 5
所以的数学期望E    1 2 3  ,
15 5 15 3
5
即这五个人去看《热辣滚烫》的人数的数学期望为 . ..................15分
3
18.（17分）
   
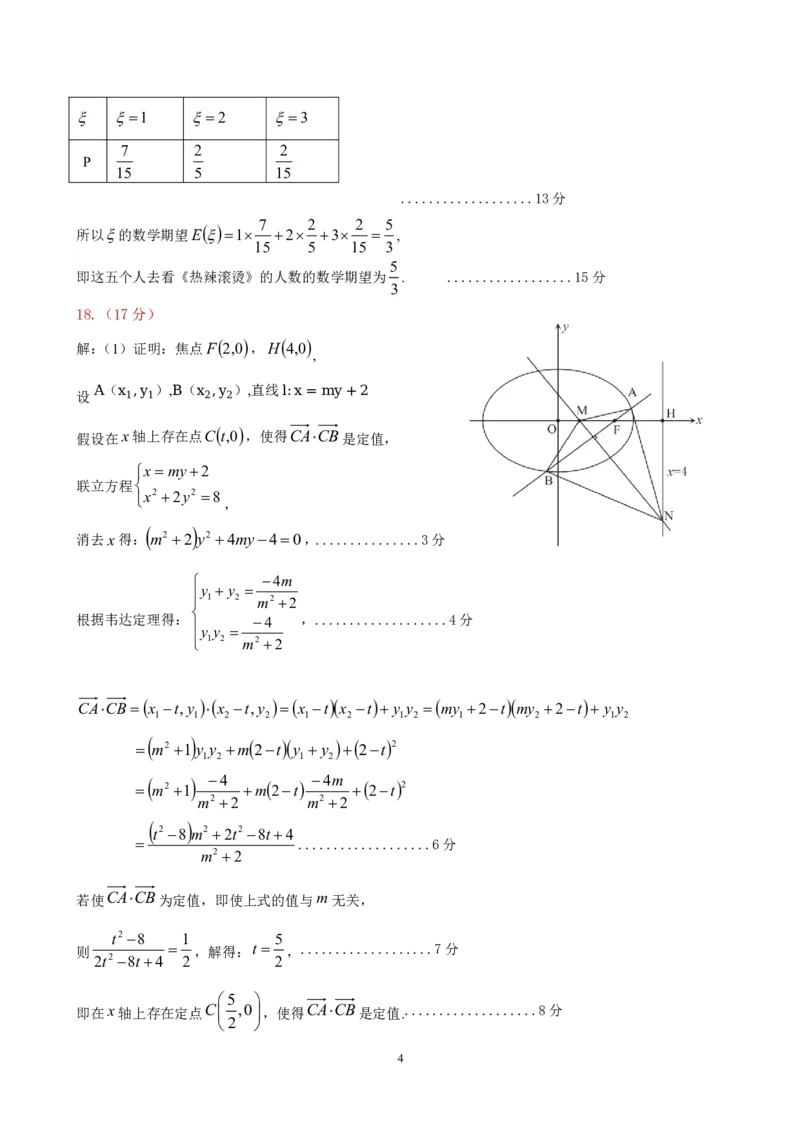
解：（1）证明：焦点F 2,0 ，H 4,0
,
（ ）, （ ）,直线
设
A x1,y1 B x2,y2 l:x= my+2
假设在x轴上存在点C  t,0  ，使得CACB是定值，
xmy2
联立方程
x2 2y2 8
，
 
消去x得： m2 2 y2 4my40，...............3分
 4m
y  y 
  1 2 m2 2

根据韦达定理得： 4 ，...................4分

y y 
  1 2 m2 2
         
CACB  x t,y  x t,y  x t x t  y y  my 2t my 2t  y y
1 1 2 2 1 2 1 2 1 2 1 2
  m2 1  y y m  2t  y  y    2t 2
1 2 1 2
  m2 1  4 m  2t  4m   2t 2
m2 2 m2 2
 
t2 8 m2 2t2 8t4
 ...................6分
m2 2
若使CACB为定值，即使上式的值与m无关，
t2 8 1 5
则  ，解得：t  ，...................7分
2t2 8t4 2 2
5 
即在x轴上存在定点C ,0，使得CACB是定值. ...................8分
2 
4（2）方法一：
  y  y 2m 2m 4
设AB的中点为E x ,y ，则y  1 2  ，x my 2m 2 ，即
0 0 0 2 m2 2 0 0 m2 2 m2 2
 4 2m 
E , ，...................9分
m2 2 m2 2
2m  4 
AB的中垂线方程为 y mx ，...................10分
m2 2  m2 2
2  2 
令 y 0，得x  ，所以M ,0...................11分
M m2 2 m2 2 
 4m  2 4
AB  1m2 y  y  1m2  y  y 2 4y y  1m2   4
1 2 1 2 1 2 m2 2 m2 2
 
4 21m2
化简得： AB  ，...................13分
m2 2
2 4 2 1m2
ME  1m2 x x  1m2   ，...................14分
M E m2 2 m2 2 m2 2
 
4 41m2 1m2
NE  1m2 x x  1m2 4  ，...................15分
N E m2 2 m2 2
2 1m2 4

1m2

1m2 8

1m2
2
1
ME NE     AB 2 ，...................16分
m2 2 m2 2  m2 2 2 4
根据相交弦定理得A,M,B,N 四点共圆....................17分
方法二：
因为MA  x x ,y  y  ，NA  x x ,y  y 
1 M 1 M 1 N 1 N
     
MANA x x x x  y  y y  y
1 M 1 N 1 M 1 N ...................10分
     
 my 2x my 2x  y  y y  y
1 M 1 N 1 M 1 N
  m2 1  y 2   4x x  m y  y  y   2x  2x   y y
1 M N M N 1 M N M N
   
  4m m2 1 4 m2 1
 m2 1 y 2  y 
1 m2 2 1 m2 2
  4m 4 
 m21 y2 y  
 1 m22 1 m22
5
学科网（北京）股份有限公司m2 1  
 m2 2 y 2 4my 4 ，...................14分
m2 2 1 1
 
因为 y 是方程 m2 2 y2 4my40的一个根，
1
  ，...................15分
所以 m2 2 y 2 4my 40
1 1
因此MANA0，即MAN 90，
根据四边形AMBN 的对称性知MBN 90，...................16分
所以A,M,B,N 四点共圆....................17分
19.（17分）
解：（1）证明：设 ，
nπ
bn =an+cos
2
因
∗
+1 =   +2+    2 +    2  ∈ 
 ...................2分
n+1 π     n+1 π
bn+1 =an+1+cos 2 =   +2+    2 +    2 +cos 2

=   +2+    +    −   
...................3分2 2 2

=an+cos 2 +2= bn+2
又因 ,
π
b1 =a1+cos2 =2
 是以 为首项，以 为公差的等差数列,

an+cos 2 2 2
则 ,

an+cos 2 =2 
 ，

=2  −    2
取等差数列 ， ，则 ...................4分

=−2    +   =−    2
因 是周期为4的数列，

2
当 时， ，

∗
=4   ∈     2 =1
当 时，

∗
=4  −1  ∈     2 =0
当 时， ，

∗
=4  −2  ∈     2 =−1
当 时， ,...................5分

3 ∗
=4  −  ∈     2 =0
6 ，
即 ∗ 元素的个数为3，
+    ∈  = −1,1,0
数列 具有 ∗ 性质....................6分
+    ∈ 
（2）证明：不妨记集合 ，其中 ，
∴    3
记集合 ∗ ，其中
=   +    ∈  =  1,  2,⋯,   1   =  1+  −1  1
∗ ...................7分
=   +    ∈  =  1,  2,⋯,   2   =  1+  −1  2
则
，
+   =   −   +   −  
...................8分
=−[  1+  1+  −1  1+  2 ]+   +    =1,2,⋯,  1;  =1,2,⋯,  2
取等差数列 ， ，...................9分
则
=  1+  1+  −1  1+  2
所以 ...................10分
+   +   =   +  
因此由分布乘法计数原理∗ 的不同取值最多只有不超过 个，
+   +    ∈  ⊆   +   |  =1,2,⋯,  1;  =1,2,⋯,  2
故存在正整数 使得数列 具有 性质。...................11分
+   +    1  2
=  1  2   +     1  2
（3）不妨记集合 ，其中 .
当 时， ∗
=   +    ∈  =  1,  2,⋯     =  1+  −1  1
....................13分
≥ 2   =   −   −1 =   +   −   −1+   −1 −   −   −1
=  取  +   − ，   则−1+  是  −等1 差 − 数  1列，
当   =  时1 ，   ，...................14分
当  ≥ 2时，   +   =   +   ，−   −1+   −1 ∈  −   ,  ∈  
所以  =1  1+  1 =  1+  1 ，...................15分
∗
因为   +  的  不∈同  取值⊆最  多1+只  有1不∪超  过−   ,  个∈，   ...................16分
2
故存在   正+整  数 使得数列 具  有+1 性质.
2  Q
综上所述，若数  列=  +的1前 项和 具  有 性  质，则存在正整数 ，使得 也具有
2
性质.................  .  ..17分       =  +1    
7
学科网（北京）股份有限公司