文档内容
绝密 考试结束前
★
2023 学年第二学期浙江七彩阳光新高考研究联盟返校考
高三数学学科试题
考生须知:
1.本试卷共 4页,满分150分,考试时间 120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号.
3.所有答案必须写在答题卷上,写在试卷上无效.
4.考试结束后,只需上交答题卷.
一、单项选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.若M,N 是I 的非空子集,M ∪N =M ,则( )
A.M ⊆ N B.N ⊆ M C.N ⊆ M D.M ⊆ N
I I
2.若( 1−i ) z =1+ 3i(i是复数单位),则 z =( )
A.1 B. 2 C. 3 D.2
6 6
1 1
3.x+
+ x−
的展开式中含x2项的系数为( )
x x
A.-30 B.0 C.15 D.30
4.设a,b为正实数,则“a >b”是“2a >log b”的( )
2
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.某校1000名学生参加数学期末考试,每名学生的成绩服从X ∼ N
( 105,152)
,成绩不低于120分为优秀,
依此估计优秀的学生人数约为( )
A.23 B.46 C.159 D.317
附:若ξ∼ N
( µ,σ2)
,则P(µ−σ<ξ<µ+σ)=0.6827,P(µ−2σ<ξ<µ+2σ)=0.9545.
6.已知a,b是异面直线,P是空间任意一点,存在过P的平面( )
A.与a,b都相交 B.与a,b都平行
C.与a,b都垂直 D.与a平行,与b垂直
学科网(北京)股份有限公司7.已知抛物线C:y2 =2px(p>0)的焦点为F ,过F 作不与x轴垂直的直线l交C于A,B两点,设OAB
m
的外心和重心的纵坐标分别为m,n(O是坐标原点),则 的值为( )
n
3 1 3
A.1 B. C. D.
4 2 8
8.已知数列 { a } 的前n项和为S ,a =1,a =2,a a =a2 +n ( n∈N*) ,则下列结论不正确的是( )
n n 1 2 n n+2 n+1
A. a n+1 是递增数列 B. { a2 −a2} 是递增数列
a n+1 n
n
a
C.S <1023 D. n+1 <3
10 a
n
二、多项选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的四个选项中,有多项符
合题目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9.已知向量a =( 1,1 ) ,b =(−2,0 ),则下列结论正确的是( )
3
A.|a|=|b | B.a与b 的夹角为 π
4
C. ( a +b ) ⊥a D.b 在a 上的投影向量是 (−1,−1 )
π π
10.已知函数 f ( x )=2sin ωx− (ω>0)图象关于点 ,0中心对称,则下列结论正确的是( )
6 4
( )
A. f x 的最小正周期3π
π
B. f =1
2
C. f ( x ) 的图象关于直线x=π对称
π
D. f ( x ) 的图象向左平移 个单位长度后关于y轴对称
4
( ) ( )
11.已知函数 f x ,g x 定义域为R ,且
f ( x ) g ( y )− f ( y ) g ( x )= f ( x− y ) ,g ( x ) g ( y )− f ( x ) f ( y )= g ( x− y ) ,g ( 0 )≠0,则下列结论正确的
是( )
( )
A. f x 为奇函数
( )
B.g x 为偶函数
C.若 f
(
1
)+g (
1
)=1,则
f
(
100
)−g (
100
)=1
学科网(北京)股份有限公司D.若 f
(
1
)−g (
1
)=1,则
f
(
100
)+g (
100
)=1
三、填空题:本题共 3小题,每小题 5分,共 15分.
12.一个宿舍的6名同学被邀请参加一个晚会,如果其中甲和乙两位同学要么都去,要么都不去,则不同去法
的种数为__________.(用数字作答)
π
13.函数 f ( x )=2cosx− +sin2x ( x∈R ) 的值域为__________.
4
5
14.已知正四面体ABCD的边长为1,P是空间一点,若PA2 +PB2 +PC2 +PD2 = ,则PA的最小值为
3
__________.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知等差数列 { a } 的各项均为正数,a =2,a +a =5a .
n 1 5 9 3
{ }
(1)求数列 a 的通项公式;
n
(2)若数列 { b } 满足b =1,a b =a b ( n∈N*) ,求 { b } 的通项公式及其前n项和S .
n 1 n n n+2 n+1 n n
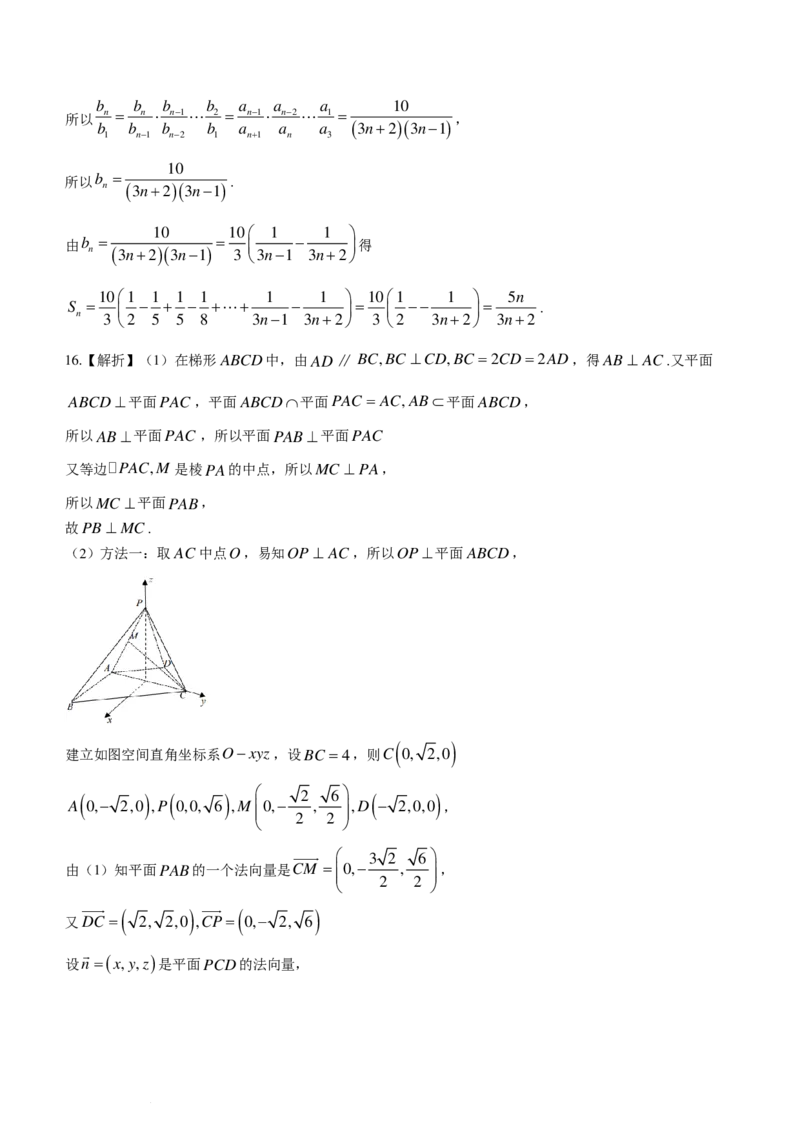
16.(15分)如图,四棱锥P−ABCD中,平面PAC ⊥平面ABCD,PAC 为等边三角形,AD∥ BC,
BC ⊥CD,BC =2CD=2AD,M 是棱PA的中点.
(1)证明:PB⊥MC;
(2)求平面PAB与平面PCD所成角的余弦值.
17.(15分)许多小朋友热衷于“套娃娃”游戏.在一个套娃娃的摊位上,若规定小朋友套娃娃成功1次或套4
1
次后游戏结束,每次套娃娃成功的概率为 ,每次套娃娃费用是10元.
3
(1)记随机变量X 为小朋友套娃娃的次数,求X 的分布列和数学期望;
(2)假设每个娃娃价值18元,每天有30位小朋友到此摊位玩套娃娃游戏,求摊主每天利润的期望.
学科网(北京)股份有限公司x2 x2
18.(17分)如图,已知椭圆C : + y2 =1,双曲线C : − y2 =1(x>0).P是C 的右顶点,过P作直线
1 2 2 2 1
l 分别交C 和C 于点A,C ,过P作直线l 分别交C 和C 于点B,D,设l ,l 的斜率分别为k ,k .
1 1 2 2 1 2 1 2 1 2
(1)若直线AB过椭圆C 的右焦点,求k ⋅k 的值;
1 1 2
(2)若k ⋅k =−1,求四边形ABCD面积的最小值.
1 2
19.(17分)设实数a >0,已知函数 f ( x )=ex −2ax+aln ( ax ) .
(1)当a =1时,求函数y = f ( x ) 在 ( 1, f ( 1 )) 处的切线方程;
(2)若 f ( x )≥0在x∈[ 1,+∞) 上恒成立,求a的取值范围.
学科网(北京)股份有限公司2023 学年第二学期浙江七彩阳光新高考研究联盟返校考
高三数学参考答案
一、单项选择题:本题共 8小题,每小题 5分,共 40分,在每小题给出的四个选项中,只有一
项是符合题目要求的.
题号 1 2 3 4 5 6 7 8
答案 B B D A C A D C
a a n a a
8.提示:由题意易得a >0,由a a =a2 +n得 n+2 = n+1 + > n+1 ≥ 2 =2,所以A正确;且
n n n+2 n+1 a a a a a a
n+1 n n n+1 n 1
a a a
a = n ⋅ n−1 2 >2n−1,所以S >1+2++29 =210 −1=1023,故C错误;
n a a a 10
n−1 n−2 1
a2 +a2
由上面知 { a } 也是递增数列,所以a2 +n=a a < n n+2 ,即
n n+1 n n+2 2
a2 −a2 >a2 −a2 +2n>a2 −a2,所以B正确;
n+2 n+1 n+1 n n+1 n
a a n a n a n
由上得 n+2 = n+1 + < n+1 + = n+1 + ,累加得
a a a a a 2n−1⋅2n a 22n−1
n+1 n n n+1 n n
a a 1 2 3 n−1
n+1 < 2 + + + ++ ( n≥2 ) ,
a a 2 23 25 22n−3
n 1
1 2 3 n−1 8 3n+1
用错位相减法可求得 + + ++ = − ( n≥2 ),
2 23 25 22n−3 9 9⋅22n−3
a 8 3n+1
所以 n+1 =2+ − <3,故D正确.
a 9 9⋅22n−3
n
二、多项选择题:本题共 3小题.每小题 6分,共 18分.在每小题给出的四个选项中,有多项符
合题目要求,全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
题号 9 10 11
答案 BCD BC ABD
11.提示:由 f ( x ) g ( y )− f ( y ) g ( x )= f ( x− y ) 得 f ( y ) g ( x )− f ( x ) g ( y )= f ( y−x ) ,
所以 f ( y−x )=−f ( x− y ) ,故 f ( x ) 是奇函数,所以A正确;
由g ( x ) g ( y )− f ( x ) f ( y )= g ( x− y ) 得g ( y ) g ( x )− f ( y ) f ( x )= g ( y−x ) ,
所以g ( y−x )= g ( x− y ) ,故g ( x ) 是偶函数,所以B正确;
学科网(北京)股份有限公司由题意得 f ( x− y )−g ( x− y )= f ( x ) g ( y )− f ( y ) g ( x )−g ( x ) g ( y )+ f ( x ) f ( y )
=
f ( y )+g ( y )
⋅
f ( x )−g ( x )
,令y =1得 f ( x−1 )−g ( x−1 )=
f ( 1 )+g ( 1 )
f ( x )−g ( x )
由 f ( x ) 是奇函数得 f ( 0 )=0,且
g ( 0 ) ]2 −
f ( 0 ) ]2 = g ( 0 ) ,g ( 0 )≠0,解得g ( 0 )=1
当 f ( 1 )+g ( 1 )=1时, f ( 100 )−g ( 100 )=
f ( 0 )−g ( 0 )
=−1,所以C错误.
由题意得 f ( x− y )+g ( x− y )= f ( x ) g ( y )− f ( y ) g ( x )+g ( x ) g ( y )− f ( x ) f ( y )
=
g ( y )− f ( y )
⋅
f ( x )+g ( x )
,令y =1得 f ( x−1 )+g ( x−1 )=
g ( 1 )− f ( 1 )
f ( x )+g ( x )
当 f ( 1 )−g ( 1 )=1时, f ( 100 )+g ( 100 )=(−1)100
f ( 0 )+g ( 0 )
=1,所以D正确.
三、填空题:本题共 3小题,每小题 5分,共 15分.
3 6
12.32; 13. − ,3 ; 14. ;
2 6
6
15.提示:设O是正四面体ABCD内切球的球心,由体积法可求正四面体ABCD的内切球半径为 ,正四
12
6
面体ABCD的外接球半径为 ,则
4
PA2 +PB2 +PC2 +PD2 = PA
2
+PB
2
+PC
2
+PD
2
=(PO+OA)2 +(PO+OB)2 +(PO+OC)2 +(PO+OD)2
2 ( ) 2
=4PO +2PO OA+OB+OC+OD +4OA
2
6 3 5 6
=4PO2 +0+4 =4PO2 + = ,即PO= ,
4 2 3 12
6 6 6
所以P是正四面体ABCD内切球上一点,故PA的最小值为OA−PA= − = .
4 12 6
四、解答题:本题共 5小题,共 77分解答应写出文字说明、证明过程或演算步骤.
15.【解析】(1)设 { a } 的公差为d ,由题意得,2a +12d =5 ( a +2d ) ,所以,d =3
n 1 1
故, { a } 的通项公式为a =a +( n−1 ) d =3n−1.
n n 1
b a 3n−1
(2)由a b =a b 得, n+1 = n = ,
n n n+2 n+1 b a 3n+5
n n+2
学科网(北京)股份有限公司b b b b a a a 10
所以 n = n ⋅ n−1 2 = n−1 ⋅ n−2 1 = ,
b b b b a a a ( 3n+2 )( 3n−1 )
1 n−1 n−2 1 n+1 n 3
10
所以b = .
n ( 3n+2 )( 3n−1 )
10 10 1 1
由b = = − 得
n ( 3n+2 )( 3n−1 ) 3 3n−1 3n+2
101 1 1 1 1 1 101 1 5n
S = − + − ++ − = −− = .
n 3 2 5 5 8 3n−1 3n+2 3 2 3n+2 3n+2
16.【解折】(1)在梯形ABCD中,由AD∥ BC,BC ⊥CD,BC =2CD=2AD,得AB⊥ AC.又平面
ABCD⊥平面PAC ,平面ABCD∩平面PAC = AC,AB⊂平面ABCD,
所以AB⊥平面PAC ,所以平面PAB ⊥平面PAC
又等边PAC,M 是棱PA的中点,所以MC ⊥ PA,
所以MC ⊥平面PAB,
故PB⊥MC.
(2)方法一:取AC中点O,易知OP⊥ AC,所以OP⊥平面ABCD,
( )
建立如图空间直角坐标系O−xyz,设BC =4,则C 0, 2,0
( ) ( ) 2 6 ( )
A 0,− 2,0 ,P 0,0, 6 ,M 0,− , ,D − 2,0,0 ,
2 2
3 2 6
由(1)知平面PAB的一个法向量是CM =0,− , ,
2 2
( ) ( )
又DC = 2, 2,0 ,CP= 0,− 2, 6
设n
=(
x,y,z
)
是平面PCD的法向量,
学科网(北京)股份有限公司
n⋅DC =0 2x+ 2y =0
则 ⇒ ,
n⋅CP=0 − 2y+ 6z =0
( )
令z =1,可得n = − 3, 3,1 ,
n⋅CM − 6 7
所以cos n,CM = = =− ,
n CM 42 7
7
故,平面PAB与平面PCD所成角的余弦值为 .
7
方法二:延长BA和CD交于E点,连接PE,则平面PAB∩平面PCD= PE
因为由(1)MC ⊥平面PAB所以过M 作MF ⊥ PE 于F 点,连接FC,又因为CM ⊥ PE,
PE ⊥CM 所以PE ⊥面MCF ,所以PE ⊥CF 则∠MFC为平面PAB与平面PCD所成角的平面角.
7
又因为设BC =4则PB=4,MF =1,MC = 6所以CF = 7,所以cos∠MFC =
7
7
故平面PAB与平面PCD所成角的余弦值为 .
7
17.【解析】(1)由题意知,随机变量X 的取值为1,2,3,4,则
2 3
1 2 1 2 2 1 4 2 8
P ( X =1 )= ,P ( X =2 )= × = ,P ( X =3 )= × = ,P ( X =4 )= = ,
3 3 3 9 3 3 27 3 27
即X 的分布列为
X 1 2 3 4
1 2 4 8
P
3 9 27 27
1 2 4 8 65
所以E ( X )=1× +2× +3× +4× = .
3 9 27 27 27
4
2 16
(2)易知小朋友套娃娃未成功的概率为
= .,
3 81
16 65
则小朋友套娃娃成功的概率为1− = .
81 81
记摊主每天利润为Y 元,则Y 的期望为
65 65 65 2600
E ( Y )=30×
E ( X )×10− ×18
=30×
×10− ×18
= ,
81 27 81 9
2600
故摊主每天利润的期望为 元.
9
学科网(北京)股份有限公司( ) ( )
18.【解析】(1)设A x ,y ,B x ,y ,直线AB方程
1 1 2 2
为x=my+1,与椭圆方程联立,得
( )
−2m −1
m2 +2 y2 +2my−1=0,y + y = ,y y = ,
1 2 m2 +2 1 2 m2 +2
4 −2m2 +2
x +x =m ( y + y )+2= ,x x =( my +1 )( my +1 )= ,
1 2 1 2 m2 +2 1 2 1 2 m2 +2
y y y y 3+2 2
所以k ⋅k = 1 2 = 1 2 =− .
1 2 x − 2 x − 2 x x − 2 ( x +x )+2 2
1 2 1 2 1 2
( ) ( ) ( ) ( )
(2)设A x ,y ,B x ,y ,C x ,y ,D x ,y ,直线AC,BD方程分别为
1 1 2 2 3 3 4 4
x=n y+ 2,x=n y+ 2,nn =−1,
1 2 1 2
x2 −2 2n −2 2n
联立x=n y+ 2与 + y2 =1得y = 1 ,同理y = 2 ,
1 2 1 n2 +2 2 n2 +2
1 2
x2 −2 2n −2 2n
联立x=n y+ 2与 − y2 =1得y = 1 ,同理y = 2 ,
1 2 3 n2 −2 4 n2 −2
1 2
1 1
所以四边形ABCD面积为S = AC ⋅ BD = 1+n2 y − y 1+n2 y − y
2 2 1 1 3 2 2 4
1 8 2 n 8 2 n 64 n2 +n2 +2
= n2 +n2 +2⋅ 1 ⋅ 2 = 1 2
2 1 2 n4 −4 n4 −4 4 ( n2 +n2 )2 −25
1 2
1 2
5 64 ( t+2 )
令t =n 1 2 +n 2 2,易知00,矛盾.
0 x 0 x x
0 0 0
故a∈( e,+∞)
不满足题意,
综合得,a的取值范围为00恒成立,
设g
(
a
)=
f
(
1
)=e−2a+alna(a>0),g′(
a
)=lna−1,当a∈(
0,e
) 时,g′(
a
)<0,g (
a
)
在
(
0,e
)
上单调递
减,a∈( e,+∞) 时,g′(
a
)>0,g (
a
)
在
( e,+∞)
上单调递增,
所以g ( a )≥ g ( e )=0,即 f ( 1 )≥0对任意a >0恒成立.
a a a
又 f′( x )=ex −2a+ ,设h ( x )=ex −2a+ ,则h′( x )=ex − ,
x x x2
易知h′(
x
) 单调递增,所以h′(
x
)≥h′(
1
)
.
当a∈(
0,e
] 时,h′(
1
)=e−a≥0,h′(
x
)≥0,
所以h
(
x
)
单调递增,
f′(
x
)=h (
x
)≥h (
1
)=e−a≥0,
f
(
x
)
单调递增,
所以 f
(
x
)≥
f
(
1
)≥0,符合题意.
当a∈( e,+∞)
时,同解法一.
学科网(北京)股份有限公司