文档内容
绝密 考试结束前
★
2023学年第二学期浙南名校联盟寒假返校联考
高一年级数学学科 试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数
字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知集合A={x x>1},B={x −1< x<2},则AB =( )
A.(−1,+∞) B.(1,2) C.(−1,1)(1,+∞) D.(−1,2)
2.已知 f(x)是定义在R上的偶函数,且当x∈(−∞,0]时, f(x)= x2 −ex +1,则当x∈(0,+∞)时, f(x)=
( )
A.x2 −ex +1 B.x2 −e−x +1 C.x2 +e−x +1 D.−x2 +e−x −1
3.“sinα>0”是“α是第一象限角”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
1
4.设α是第二象限角,P(x,1)为其终边上一点,且cosα= x,则tanα=( )
3
2 2 2
A.−2 2 B.− C.− D.−
2 4 8
1−a
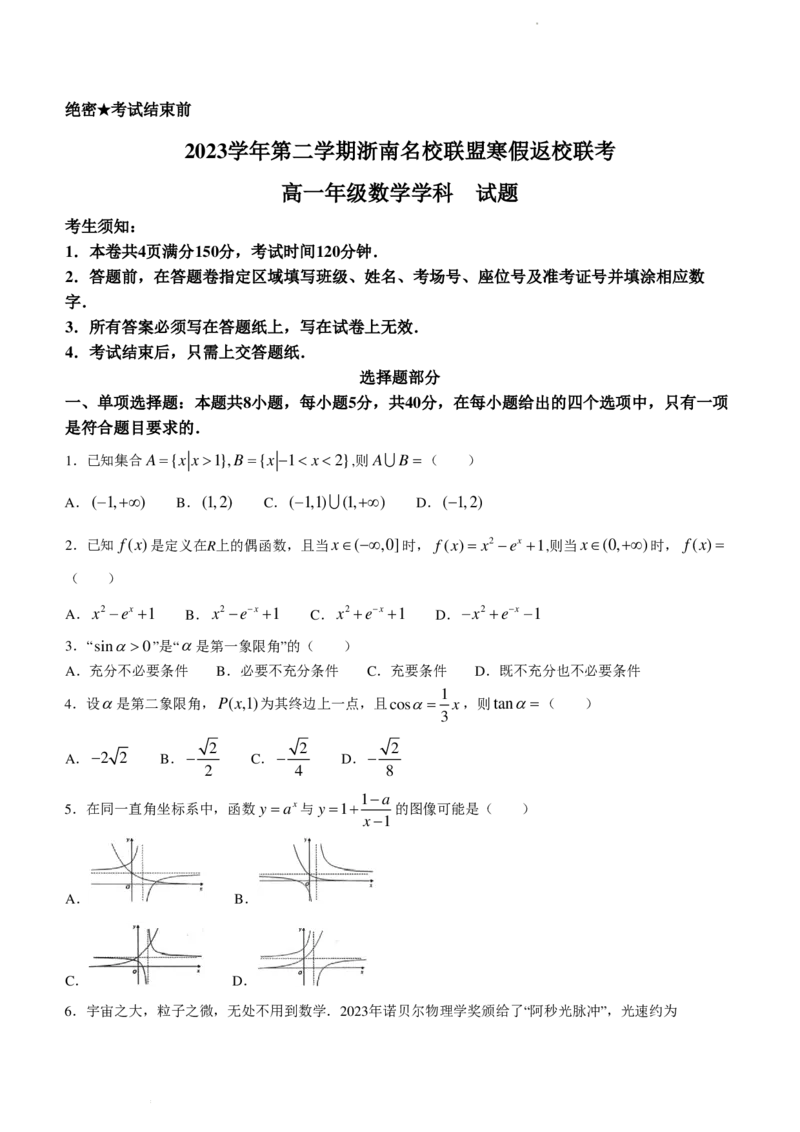
5.在同一直角坐标系中,函数y =ax与y =1+ 的图像可能是( )
x−1
A. B.
C. D.
6.宇宙之大,粒子之微,无处不用到数学.2023年诺贝尔物理学奖颁给了“阿秒光脉冲”,光速约为
学学科科网网((北北京京))股股份份有有限限公公司司3×108m/s, 1阿秒等于10−18s.一尺之棰,日取其半,万世不竭,一根1米长的木棰,第一次截去总长的一
半,以后每次截去剩余长度的一半,至少需要截( )次才能使其长度小于光在1阿秒内走的距离.(参考
数据:lg2≈0.30,lg3≈0.48)
A.30 B.31 C.32 D.33
af(a)−bf(b)
7.已知函数 f(x)是定义在R上的奇函数,若∀a,b∈[0,+∞),且a ≠b,都有 <0成立,则不等
a−b
( ) 2
式tf t2 −
+1 f(t+2)<0的解集为( )
t
A.(−∞,−1)(2,+∞) B.(−1,0)(2,+∞) C.(−1,2) D.(−∞,−1)(0,+∞)
1 1 2025
8.已知a=1−cos ,b= ,c=log ,则a,b,c的大小关系为( )
2024 2024 2 2024
A.bb, c>d ,则a−d >b−c B.若a >b,则ac>bc
1 1 a+2b b
C.若ab≠0,a >b,则 < D.若a>b>0,则 >
a b 2a+b a
π
10.设函数 f(x)=coswx+ (w>0),已知 f(x)在[0,π]有且仅有3个零点,下述结论中,正确的是
3
( )
A. f(x)=−1在[0,π]有且仅有1个解
13 19
B.ω的取值范围是 ,
6 6
π
C. f(x)在 0, 单调递减
6
3 π π 3
D.若A,B是直线y = 与曲线y = f(x)的两个交点,且| AB|= ,则 f =−
2 9 6 2
2f(xy)
11.已知定义在(−∞,0)(0,+∞)上的函数 f(x)满足 f(x)− f(y)= ,当x<0时, f(x)<0,且
f(y−x)
f(1)=2,则( )
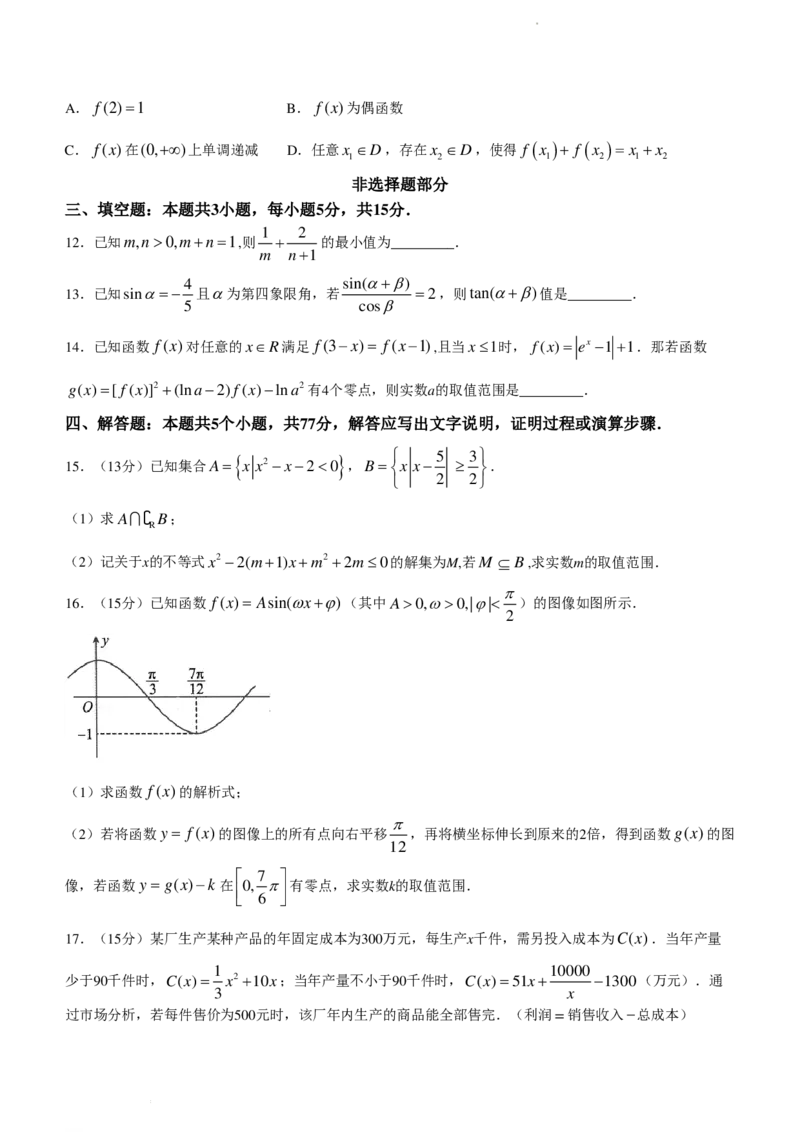
学学科科网网((北北京京))股股份份有有限限公公司司A. f(2)=1 B. f(x)为偶函数
C. f(x)在(0,+∞)上单调递减 D.任意x ∈D,存在x ∈D,使得 f ( x )+ f ( x )= x +x
1 2 1 2 1 2
非选择题部分
三、填空题:本题共3小题,每小题5分,共15分.
1 2
12.已知m,n>0,m+n=1,则 + 的最小值为_________.
m n+1
4 sin(α+β)
13.已知sinα=− 且α为第四象限角,若 =2,则tan(α+β)值是_________.
5 cosβ
14.已知函数 f(x)对任意的x∈R满足 f(3−x)= f(x−1),且当x≤1时, f(x)= ex −1+1.那若函数
g(x)=[f(x)]2 +(lna−2)f(x)−lna2有4个零点,则实数a的取值范围是_________.
四、解答题:本题共5个小题,共77分,解答应写出文字说明,证明过程或演算步骤.
{ } 5 3
15.(13分)已知集合A= x x2 −x−2<0 ,B=x x− ≥ .
2 2
(1)求A B;
R
(2)记关于x的不等式x2 −2(m+1)x+m2 +2m≤0的解集为M,若M ⊆ B,求实数m的取值范围.
π
16.(15分)已知函数 f(x)= Asin(ωx+ϕ)(其中A>0,ω>0,|ϕ|< )的图像如图所示.
2
(1)求函数 f(x)的解析式;
π
(2)若将函数y = f(x)的图像上的所有点向右平移 ,再将横坐标伸长到原来的2倍,得到函数g(x)的图
12
7
像,若函数y = g(x)−k 在 0, π 有零点,求实数k的取值范围.
6
17.(15分)某厂生产某种产品的年固定成本为300万元,每生产x千件,需另投入成本为C(x).当年产量
1 10000
少于90千件时,C(x)= x2 +10x;当年产量不小于90千件时,C(x)=51x+ −1300(万元).通
3 x
过市场分析,若每件售价为500元时,该厂年内生产的商品能全部售完.(利润=销售收入−总成本)
学学科科网网((北北京京))股股份份有有限限公公司司(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
18.(17分)已知函数 f(x)=asinx+ 1+cosx + 1−cosx
(1)若a=0,x∈[0,π],求 f(x)的值域;
1 1
(2)若a>0,x∈[0,2π]都有 f(x)≥ a+ 恒成立,求a的取值范围.
2 2
aex +1
19.(17分)已知函数 f(x)= (a∈R)为奇函数.
ex −1
(1)求a的值;
(2)设函数g(x)=lnx+sinx,
i.证明:y = g(x)有且只有一个零点;
e+1
ii.记函数y = g(x)的零点为x ,证明: f ( sinx )> .
0 0 e−1
学学科科网网((北北京京))股股份份有有限限公公司司