文档内容
2024 年浙江省高考数学模拟卷
命题:浙江省温州中学
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
z
1.已知复数z满足 =1+i,则z的共轭复数z在复平面上对应的点位于( )
3−i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设集合M = { x x=2k+1,k∈Z } ,N = { x x=3k−1,k∈Z } ,则M N =( )
{ } { }
A. x x=2k+1,k∈Z B. x x=3k−1,k∈Z
{ } { }
C. x x=6k+1,k∈Z D. x x=6k−1,k∈Z
( ) ( )
3.已知不共线的平面向量a,b满足 a+λb ∥ λa+2b ,则正数λ=( )
A.1 B. 2 C. 3 D.2
4.传输信号会受到各种随机干扰,为了在强干扰背景下提取微弱信号,可用同步累积法.设s是需提取的
确定信号的值,每隔一段时间重复发送一次信号,共发送m次,每次接收端收到的信号
X =s+ε( i =1,2,3,,m ),其中干扰信号ε为服从正态分布N ( 0,σ2 ) 的随机变量,令累积信号
i i i
m
Y =∑X ,则Y服从正态分布N ( ms,mσ2 ) ,定义信噪比为信号的均值与标准差之比的平方,例如X 的
i 1
i=1
2
s
信噪比为
,则累积信号Y的信噪比是接收一次信号的( )倍
σ
3
A. m B.m C.m2 D.m2
π π
5.已知函数 f ( x )=cos2x+ ,则“θ= +kπ ( k∈Z )”是“ f ( x+θ)为奇函数且 f ( x−θ)为偶
4 8
函数”的( )
A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
6.在平面直角坐标系xOy中,直线y =2x+t与圆C:x2 + y2 −2x+4y =0相交于点A,B,若
2π
∠ACB= ,则t =( )
3
1 11 3 13
A.− 或− B.-1或-6 C.− 或− D.-2或-7
2 2 2 2
7.已知甲、乙、丙、丁、戊5人身高从低到高,互不相同,将他们排成相对身高为“高低高低高”或
“低高低高低”的队形,则甲、丁不相邻的不同排法种数为( )
A.12 B.14 C.16 D.18
学科网(北京)股份有限公司x2 y2
8.已知双曲线 − =1 ( a,b>0 )上存在关于原点中心对称的两点A,B,以及双曲线上的另一点C,
a2 b2
使得△ABC为正三角形,则该双曲线离心率的取值范围是( )
A. ( 2,+∞ ) B. ( 3,+∞ ) C.( 2,+∞) D. 2 3 ,+∞
3
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9.已知函数 f ( x )=( x+1 ) ex,则下列结论正确的是( )
1
A. f ( x )在区间(−2,+∞)上单调递增 B. f ( x )的最小值为−
e2
C.方程 f ( x )=2的解有2个 D.导函数 f′( x )的极值点为-3
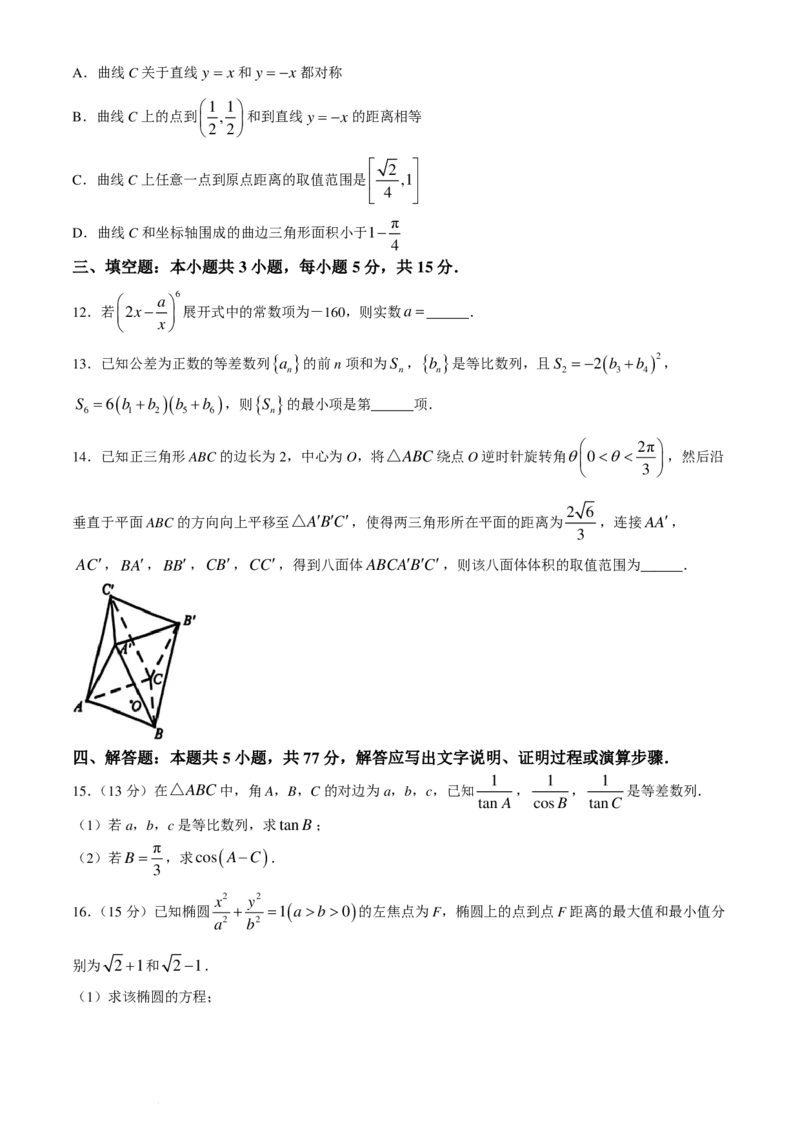
10.南丁格尔是一位英国护士、统计学家及社会改革者,被誉为现代护理学的奠基人.1854年,在克里米
亚战争期间,她在接到英国政府的请求后,带领由38名志愿女护士组成的团队前往克里米亚救治伤员,
并收集士兵死亡原因数据绘制了如下“玫瑰图”.图中圆圈被划分为12个扇形,按顺时针方向代表一年中
的各个月份.每个扇形的面积与该月的死亡人数成比例.扇形中的白色部分代表因疾病或其他原因导致的
死亡,灰色部分代表因战争受伤导致的死亡.右侧图像为1854年4月至1855年3月的数据,左侧图像为
1855年4月至1856年3月的数据.下列选项正确的为( )
A.由于疾病或其他原因而死的士兵远少于战场上因伤死亡的士兵
B.1854年4月至1855年3月,冬季(12月至来年2月)死亡人数相较其他季节显著增加
C.1855年12月之后,因疾病或其他原因导致的死亡人数总体上相较之前显著下降
D.此玫瑰图可以佐证,通过改善军队和医院的卫生状况,可以大幅度降低不必要的死亡
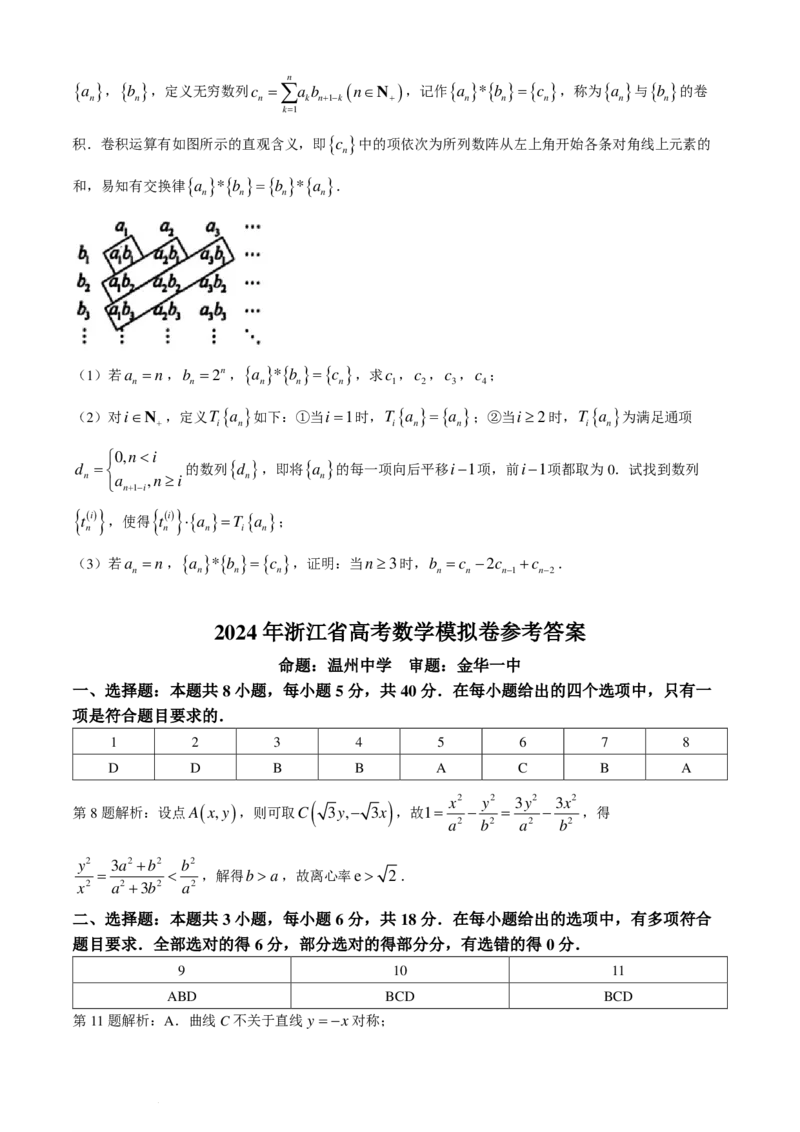
11.如图,平面直角坐标系上的一条动直线l和x,y轴的非负半轴交于A,B两点,若 OA + OB =1恒成
立,则l始终和曲线C: x + y =1相切,关于曲线C的说法正确的有( )
学科网(北京)股份有限公司A.曲线C关于直线y = x和y =−x都对称
1 1
B.曲线C上的点到 , 和到直线y =−x的距离相等
2 2
2
C.曲线C上任意一点到原点距离的取值范围是 ,1
4
π
D.曲线C和坐标轴围成的曲边三角形面积小于1−
4
三、填空题:本小题共 3小题,每小题 5分,共 15分.
6
a
12.若 2x−
展开式中的常数项为-160,则实数a=______.
x
13.已知公差为正数的等差数列{ a }的前n项和为S ,{ b }是等比数列,且S =−2 ( b +b )2,
n n n 2 3 4
S =6 ( b +b )( b +b ),则{ S }的最小项是第______项.
6 1 2 5 6 n
2π
14.已知正三角形ABC的边长为2,中心为O,将△ABC绕点O逆时针旋转角θ 0<θ<
,然后沿
3
2 6
垂直于平面ABC的方向向上平移至△A′B′C′,使得两三角形所在平面的距离为 ,连接AA′,
3
AC′,BA′,BB′,CB′,CC′,得到八面体ABCA′B′C′,则该八面体体积的取值范围为______.
四、解答题:本题共 5小题,共 77分,解答应写出文字说明、证明过程或演算步骤.
1 1 1
15.(13分)在△ABC中,角A,B,C的对边为a,b,c,已知 , , 是等差数列.
tanA cosB tanC
(1)若a,b,c是等比数列,求tanB;
π
(2)若B = ,求cos ( A−C ).
3
x2 y2
16.(15分)已知椭圆 + =1 ( a >b>0 )的左焦点为F,椭圆上的点到点F距离的最大值和最小值分
a2 b2
别为 2+1和 2−1.
(1)求该椭圆的方程;
学科网(北京)股份有限公司(2)对椭圆上不在上下顶点的任意一点P,其关于y轴的对称点记为P′,求 PF + P′F ;
(3)过点Q ( 2,0 )作直线交椭圆于不同的两点A,B,求△FAB面积的最大值.
17.(15分)如图,已知三棱台ABC−ABC ,AB= BC =CA= AA = BB =2,AB =4,点O为线
1 1 1 1 1 1 1
段AB 的中点,点D为线段OA 的中点.
1 1 1
(1)证明:直线AD∥平面OCC ;
1
(2)若平面BCC B ⊥平面ACC A ,求直线AA 与平面BCC B 所成线面角的大小.
1 1 1 1 1 1 1
18.(17分)第二次世界大战期间,了解德军坦克的生产能力对盟军具有非常重要的战略意义.已知德军
的每辆坦克上都有一个按生产顺序从1开始的连续编号.假设德军某月生产的坦克总数为N,随机缴获该
月生产的n辆(n< N )坦克的编号为X ,X ,…,X ,记M =max { X ,X ,,X },即缴获坦克
1 2 n 1 2 n
中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
X + X ++ X
甲同学根据样本均值估计总体均值的思想,用X = 1 2 n 估计总体的均值,因此
n
N N ( N +1 ) N +1
NX ≈∑i = ,得X ≈ ,故可用Y =2X −1作为N的估计.
2 2
i=1
乙同学对此提出异议,认为这种方法可能出现Y a,故离心率e> 2.
x2 a2 +3b2 a2
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9 10 11
ABD BCD BCD
第11题解析:A.曲线C不关于直线y =−x对称;
学科网(北京)股份有限公司 1 2 1 2 x+ y
B.设C上一点P ( x,y ),则 x− + y− = ⇔ x2 + y2 −2x−2y−2xy+1=0,而
2 2 2
x + y =1⇔ x+ y+2 xy =1⇒4xy =( 1−x− y )2 ⇔ x2 + y2 −2x−2y−2xy+1=0,成立;
2
( )2
( x+ y )2 1 x + y 1
C.OP2 = x2 + y2 ≤ x + y =1,x2 + y2 ≥ ≥ = ,成立;
2 2 2 8
D.P ( x,y )到点A ( 1,1 )的距离 AP 2 =( x−1 )2 +( y−1 )2 = x2 + y2 −2x−2y+2=2xy+1≥1,故曲线C
π
位于圆( x−1 )2 +( y−1 )2 =1的左下部分四分之一圆弧的下方,故围成面积小于1− .
4
三、填空题:本小题共 3小题,每小题 5分,共 15分.
12 13 14
8 2
1 2 2 2,
3
注:第14题区间开闭写错不扣分.
S S S
第13题解析:0= 2 + 6 =2⋅ 4 ⇒S =0,故{ S }的最小项是第2项.
2 6 4 4 n
第14题解析:V =V +V +V +V
ABCA′B′C′ A′−ABC C−A′B′C′ A′B′−BC A′C′−AC
1 3 2 6 1 π 2 6 1 2 6
= ⋅ ⋅22⋅ ⋅2+ ⋅2⋅2⋅sin θ+
⋅ + ⋅2⋅2⋅sinθ⋅
3 4 3 6 3 3 6 3
4 π 8 2
= 21+sin θ+ ∈ 2 2, .
3 6 3
四、解答题:本题共 5小题,共 77分,解答应写出文字说明、证明过程或演算步骤.
15.(13分)
(1)由b2 =ac得sin2 B=sinAsinC,
2 1 1 2 cosA cosC sinB
= + ⇔ = + = ,
cosB tan A tanC cosB sin A sinC sin AsinC
2 sinB 1
故 = ⇔ tanB= .
cosB sin2 B 2
π 1 3
(2)若B = ,则sinAsinC = sinBcosB= ,
3 2 8
1 3 1
又由cos ( A+C )=cosAcosC−sinAsinB=− 得cosAcosC = − ,
2 8 2
学科网(北京)股份有限公司3 1 3 3−2
故cos ( A−C )= − + = .
8 2 8 4
1
注:第二问直接利用积化和差公式sinAsinC = ( cos ( A−C )−cos ( A+C )) ,写对公式给3分,条件代
2
入正确化简给3分,最终答案1分.
16.(15分)
(1)记c= a2 −b2 ,则a+c= 2+1,a−c= 2−1,
x2
解得a= 2,c=1,故椭圆的方程为 + y2 =1.
2
(2)记椭圆的右焦点为F′,则 PF + P′F = PF + PF′ =2a=2 2.
(3)设A ( x ,y ),B ( x ,y ),直线AB的方程为x=my+2,
1 1 2 2
x=my+2
( )
联立x2 ,得 m2 +2 y2 +4my+2=0,
+ y2 =1
2
2 2⋅ m2 −2 1 3 2⋅ m2 −2
故 y − y = ,S = ⋅3⋅ y − y = ,
1 2 m2 +2 △ABF 2 1 2 m2 +2
3 2t 3 2t 3 2
令t = m2 −2 >0,则S = ≤ = ,当m=± 6 时取到等号.
△ABF t2 +4 2⋅2t 4
17.(15分)
(1)取AB中点M,则CM∥CO,故O,M,C,C 共面,
1 1
由AM与OD平行且相等得平行四边形ODAM,故AD∥OM ,
故AD∥平面OCC .
1
(2)法1(建系):以O为原点,OM ,OA 为x,y轴正方向,垂直于平面ABB A 向上为z轴正方向,
1 1 1
建立空间直角坐标系Oxyz.
( ) 1+cosα
设C 3 ( 1−cosα) ,0, 3sinα ,表示出平面ACC A 的法向量n = 1, 3, ,
1 1 1 sinα
1+cosα
由对称性得平面BCC B 的法向量n = 1,− 3, ,
1 1 2 sinα
1
故n ⋅n =0,解得cosα= ,
1 2
3
学科网(北京)股份有限公司2 3 2 6 ( ) ( )
故C ,0, ,n = 1, 3, 2 ,n = 1,− 3, 2 ,
3 3 1 1
AA,n
2 π
记所求线面角为θ,则sinθ= 1 2 = ,故θ= .
AA n 2 4
1 2
法2(综合法):连接CA ,CB ,取AC 中点N,则CN = AA =1= NA = NC ,故CA ⊥CC ,
1 1 1 1 1 1 1 1 1
由平面BCC B ⊥平面ACC A ,CC =平面BCC B 平面ACC A ,故CA ⊥平面BCC B ,
1 1 1 1 1 1 1 1 1 1 1 1
故BC ⊥ AC,又由BC = AC,得BC = AC = 2,
1 1 1 1 1 1
AC 2
延长CC ,AA,BB交于点V,则所求线面角即∠AVC,而sin∠AVC = 1 = ,故直线AA 与
1 1 1 1 1 AV 2 1
1
π
平面BCC B 所成线面角的大小为 .
1 1 4
π
法3(三余弦定理):延长CC ,AA,BB交于点V,则∠BVA = ,∠AVC =∠BVC ,
1 1 1 1 1 3 1 1 1 1
由平面BCC B ⊥平面ACC A ,用三余弦定理得cos∠BVA =cos∠CVA ⋅cos∠CVB ,
1 1 1 1 1 1 1 1 1 1
2 π
因此cos∠CVA = ,故直线AA 与平面BCC B 所成线面角即为∠CVA = .
1 1 2 1 1 1 1 1 4
18.(17分)
学科网(北京)股份有限公司C2 3
(1)M =5时,最大编号为5,另2辆坦克编号有C2种可能,故P ( M =5 )= 4 = ,
4 C3 5
5
由Y