浦东新区2024届高三二模数学卷参考答案_2024年4月_01按日期_6号_2024届上海市浦东新区高三二模_2024届上海市浦东新区高三二模数学

浦东新区 2023 学年度第二学期期中教学质量检测 高三数学试卷 考生注意：1、本试卷共21道试题，满分150分，答题时间120分钟； 2、请在答题纸上规定的地方解答，否则一律不予评分． 一、填空题（本大题满分54分）本大题共有12题．考生应在答题纸相应编号的空格内直接填写结果，1-6题每个 空格填对得4分，7-12题每个空格填对得5分，否则一律得零分． 1.已知集合A0,1,2 ，集合B   x 2x 3  ，则AIB  ． 【答案】： 2 2.若复数z 12i（i是虚数单位），则zz z  ． 【答案】：42i 3.已知等差数列 a  满足a a 12，a 7，则a  ． n 1 6 4 3 【答案】：5 5  1 4.  3x2   的二项展开式中x4项的系数为 ．（用数值回答）  x 【答案】：270 5.已知随机变量X 服从正态分布N  95,2 ，若P(75 X 115)0.4，则P(X 115) ． 【答案】：0.3 6.已知 y  f x是奇函数，当x0时， f(x) x 2 3 ，则 f    8  的值是 ．  125 【答案】： 4  25 7.某校面向高一全体学生共开设3门体育类选修课，每人限选一门．已知这三门体育类 选修课的选修人数之比为 6:3:1，考核优秀率分别为20%、16%和12%，现从该年级所有选择体育类选修课的同学中任取一名，其成绩 是优秀的概率为 ． 【答案】：0.18 8.已知圆C :x2  y2 2axa2 10（a 0），圆C :x2  y2 4y50 ，若两圆相交，则实 1 2 数a的取值范围为 ． 【答案】：(0,2 3)9.已知 f(x)2x x，则不等式 f(|2x3|)3的解集为 ． 【答案】：(1,2) 10.如图，有一底面半径为1，高为3的圆柱．光源点A沿着上底面圆周作匀速运动，射出的光线始终经过圆柱轴截 面的中心．当光源点A沿着上底面圆周运动半周时，其射出的光线在圆柱内部“扫过”的面积为 ． 13 【答案】：  2 x2 y2 2 11.已知双曲线  1(a0,b0) 的焦点分别为 F 、 F ， M 为双曲线上一点，若FMF  ， a2 b2 1 2 1 2 3 21 OM  b，则双曲线的离心率为 ． 3 6 【答案】： 2        12.正三棱锥S  ABC中，底面边长AB 2，侧棱AS 3，向量a，b满足a(a AC)aAB，        b(b AC)bAS ，则 ab 的最大值为 ． 【答案】：4 二、选择题（本大题满分18分）本大题共有4题，每题有且只有一个正确答案．考生必须在答题纸的相应编号上， 将代表答案的小方格涂黑，13-14题每题选对得4分，15-16题每题选对得5分，否则一律得零分． 13.“a 1”是“直线ax2y20与直线xa1y10平行”的（ ）． A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件 【答案】：C 14.已知aR，则下列结论不恒成立的是（ ）． 1 1 1 A. a(1a) B. a  2 C.|a1||a2|3 D.sina 0 4 a 2sina 【答案】：B 15.通过随机抽样，我们绘制了如图所示的某种商品每千克价格（单位：百元）与该商品消费者年需求量（单位： 千克）的散点图．若去掉图中右下方的点A后，下列说法正确的是（ ）． A.“每千克价格”与“年需求量”这两个变量由负相关变为正相关 B.“每千克价格”与“年需求量”这两个变量的线性相关程度不变 C.“每千克价格”与“年需求量”这两个变量的线性相关系数变大 D.“每千克价格”与“年需求量”这两个变量的线性相关系数变小 【答案】：D16.设 f xa xm a xm1La xa (a 0,m10，mZ)，记 f x f x(n1,2,L,m1)， 0 m m1 1 0 m n n1 令有穷数列b 为 f x 零点的个数 n1,2,L,m1 ，则有以下两个结论： n n ①存在 f x ，使得b 为常数列； 0 n ②存在 f x ，使得b 为公差不为零的等差数列． 0 n 那么（ ）． A.①正确，②错误 B.①错误，②正确 C.①②都正确 D.①②都错误 【答案】：C 三、解答题（本大题满分78分）本大题共有5题，解答下列各题必须在答题卷的相应编号规定区域内写出必要的 步骤． 17．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分． 已知函数 y f x，其中 f xsinx．  π 3 （1）求 f  x   在x0,π 上的解；  4 2  π 1  π （2）已知g(x) 3f(x)f  x   f x f xπ，若关于x的方程gxm  在x  0,  时有解，  2 2  2 求实数m的取值范围． 7 11  1  【答案】：（1） 、 ；（2）  ,1 .   12 12  2    3 【详解】：（1）由题，原式等价于求sin  x   在x0, 上的解.  4 2 从而有 或 ，解得 或    2 7 11 x  2k x  2k ,kZ x2k x2k ,kZ 4 3 4 3 12 12 7 11 又x0, ，所以x 或x . 12 12 所以 f  x π  3 在x0,π 上的解为 7 、 11 .    4 2 12 12  π （2）由题，gx 3sin xsin  x  sin xsinxπ  2  3sinxcosxsin2x3 1cos2x  sin2x 2 2  π 1 sin 2x     6 2 1  π 故g(x)m 在x 0, 时有解   2  2  π  π 等价于msin  2x 在x  0,  时有解.  6  2 π  π 5π  π  1  可知2x    ,  , 因而sin  2x     ,1  6  6 6   6  2   1  所以，实数m的取值范围是  ,1 . 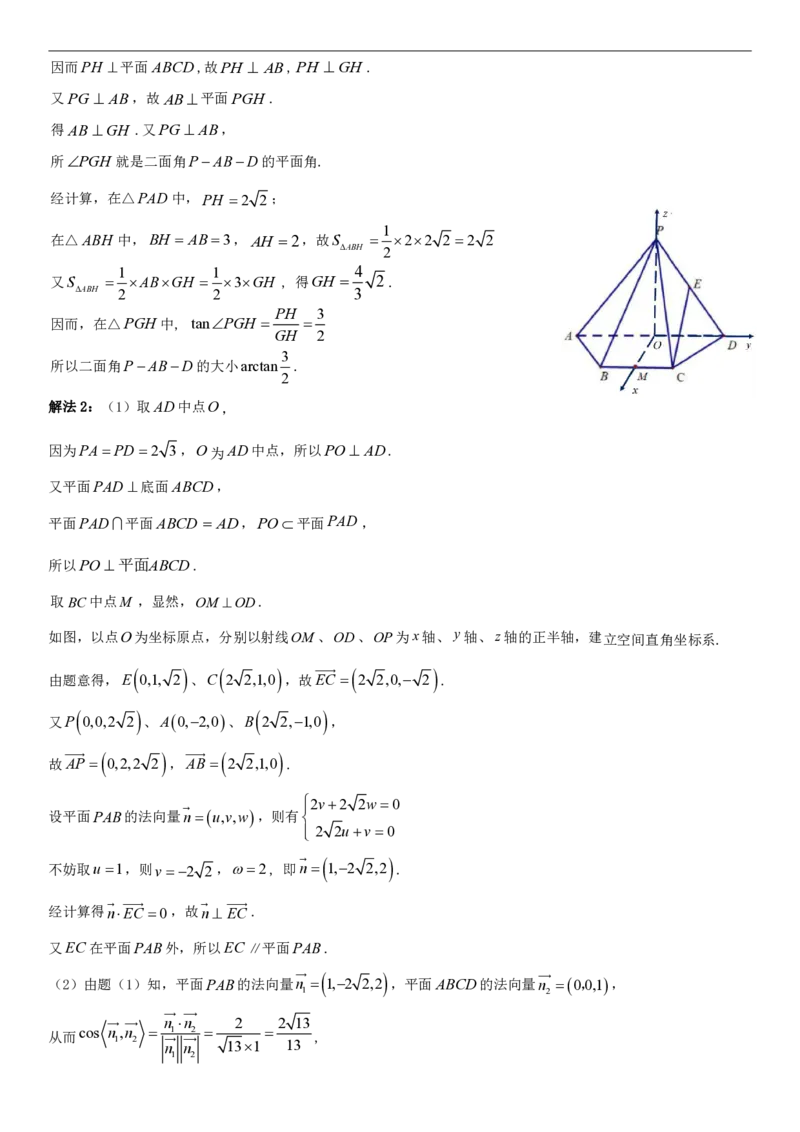   2  18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分． 在四棱锥 PABCD 中，底面 ABCD 为等腰梯形，平面 PAD  底面 ABCD ，其中 AD//BC ， AD  2BC  4，AB 3,PA PD 2 3，点E为PD中点． （1）证明：EC//平面PAB； （2）求二面角P ABD的大小． 2 【答案】：（1）证明见详解；（2）arccos 13 . 13 【详解】：解法1：（1）证明：取PA中点F，连接BF,EF ， 在△PAD中，点E为PD的中点、点F为PA的中点， 1 所以EF∥AD，EF  AD. 2 1 又BC∥AD, BC  AD . 2 因此EF∥BC，EF BC. 所以，四边形BCEF为平行四边形. 得EC∥FB，又FB平面PAB，而EC在平面PAB外， 所以，EC∥平面PAB. （2）取AD中点H ，过P作PG AB，垂足为G，连接GH 由题，PAPD  2 3，H 为AD的中点，所以PH  AD . 又平面PAD 底面ABCD， 平面PADI平面ABCD  AD，且PH 平面PAD，因而PH 平面ABCD,故PH  AB,PH GH . 又PG  AB，故AB平面PGH . 得AB GH .又PG AB， 所PGH 就是二面角PABD的平面角. 经计算，在△PAD中，PH 2 2； 1 在△ABH 中，BH  AB3，AH 2，故S  22 2 2 2 ABH 2 1 1 4 又S  ABGH  3GH , 得GH  2. ABH 2 2 3 PH 3 因而，在△PGH 中, tanPGH   GH 2 3 所以二面角PABD的大小arctan . 2 解法2：（1）取AD中点O， 因为PAPD  2 3，O为AD中点，所以PO AD. 又平面PAD 底面ABCD， 平面PADI平面ABCD  AD，PO平面PAD， 所以PO平面ABCD. 取BC中点M ，显然，OM OD. 如图，以点O为坐标原点，分别以射线OM 、OD、OP为x轴、 y轴、z轴的正半轴，建立空间直角坐标系. uuur       由题意得，E 0,1, 2 、C 2 2,1,0 ，故EC  2 2,0, 2 .     又P 0,0,2 2 、A0,2,0、B 2 2,1,0 ， uuur uuur     故AP  0,2,2 2 ，AB  2 2,1,0 . r  2v2 2w0 设平面PAB的法向量nu,v,w，则有  2 2uv 0 r   不妨取u 1，则v2 2，2, 即n 1,2 2,2 . r uuur r uuur 经计算得nEC 0，故n EC . 又EC在平面PAB外，所以EC∥平面PAB. ur uur   （2）由题（1）知，平面PAB的法向量n  1,2 2,2 ，平面ABCD的法向量n 0，0,1， 1 2 ur uur ur uur n n 2 2 13 从而 cos n,n  ur1 uur2   , 1 2 n n 131 13 1 22 因此，二面角PABD的大小为arccos 13 . 13 19．（本题满分14分）本题共有3个小题，第1小题满分4分，第2小题满分4分，第3小题满分6分． 某商店随机抽取了当天100名客户的消费金额，并分组如下： 0,200 ， 200,400 ， 400,600 ，…， 1000,1200 （单位：元），得到如图所示的频率分布直方图． （1）若该店当天总共有1350名客户进店消费，试估计其中有多少客户的消费额不少于800元； （2）若利用分层随机抽样的方法从消费不少于800元的客户中共抽取6人，再从这6人中随机抽取2人做进一 步调查，则抽到的2人中至少有1人的消费金额不少于1000元的概率是多少； （3）为吸引顾客消费，该商店考虑两种促销方案． 方案一：消费金额每满300元可立减50元，并可叠加使用； 1 方案二：消费金额每满1000元即可抽奖三次，每次中奖的概率均为 ，且每次抽奖互不影响．中奖1次当天消 3 费金额可打9折，中奖2次当天消费金额可打6折，中奖3次当天消费金额可打3折． 若两种方案只能选择其中一种，小王准备购买的商品又恰好标价1000元，请帮助他选择合适的促销方案并说 明理由． 【答案】：（1）405人；（2） 3 ；（3）选择第二种促销方，理由见详解. 5 【详解】：（1）我们利用通过抽样获得的100名客户的样本信息来估计总体的分布情况可得： 人. 3 1350 405 10 （2）当日消费金额在800,1000和1000,1200（单位：元）的人数所占比例为0.00100:0.00050 2:1， 所以抽取的6人中有2人消费金额在1000,1200（单位：元），有4人消费金额在800,1000（单位：元）. C1C1 C2 3 记“抽到的2人中至少1人消费额不少于1000元”为事件A，则PA 4 2 + 2 = ， C2 C2 5 6 6 3 所以抽到的2人中至少1人消费金额不少于1000元的概率为 . 5 （3）若选方案一，只需付款1000503850元； 若选方案二，设付款金额为X 元，则X 可分别取300、600、900、1000元，其中 1 0 1 3 1 PX 300C3 1     ， 3  3 3 27  1 1 1 2 2 PX 600C2 1     ， 3  3 3 9  1 2 1 1 4 PX 900C1 1     ， 3  3 3 9  1 3 1 0 8 PX 1000C0 1     ， 3  3 3 27 1 2 4 8 所以EX=300 600 900 1000 840.7元， 27 9 9 27 因为850840.7， 所以应选择第二种促销方案. 20．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分． x2 已知椭圆C:  y2 1，点F 、F 分别为椭圆的左、右焦点． 2 1 2 （1）若椭圆上点P满足PF  FF ，求 PF 的值； 2 1 2 1 （2）点A为椭圆的右顶点，定点Tt,0 在x轴上，若点S为椭圆上一动点，当 ST 取得最小值时点S恰与点A 重合，求实数t的取值范围； （3）已知m为常数，过点F 且法向量为1,m的直线l交椭圆于M 、N 两点，若椭圆C上存在点R满足 2 uuur uuur uuur OR OM ON （,R），求的最大值． 3 2  2  m2 2 【答案】：（1） ；（2） ,；（3） .  2  2  4 1 2 【详解】：（1）由题得，F (1,0)，设点P(1,y )，代入椭圆方程，得 y2  ，因而 PF  . 2 P P 2 2 2 3 2 由 PF  PF 2 2，得 PF  . 1 2 1 2 x2 x2 1 （2）设动点S(x,y)，则 ST 2 (xt)2 y2  x22txt21  2txt21  (x2t)2 1t2 2 2 2 1 由题， ST 取得最小值时点S恰与点A重合，即函数 y  (x2t)2 1t2在x 2处取得最小值， 2 2 又x[ 2, 2]，因而2t  2 ，得t  . 2 2  因此，实数t的取值范围为 ,.  2   （3）设M(x ,y )，N(x ,y )，R(x,y) 1 1 2 2 uur uuur uuur x x x 由OR OM ON ,得 1 2 ，  y y y 1 2 又点R在椭圆上，代入得(x x )2 2(y y )2 2， 1 2 1 2 化简得2(x2 2y2)2(x2 2y2)2(x x 2y y )2， 1 1 2 2 1 2 1 2 又点M 、N 在椭圆上，得22 22 2(x x 2y y )2（*）. 1 2 1 2 由题，可设直线l:(x1)my 0.  xmy1 联列直线与椭圆方程，得 ，得(m2 2)y2 2my10. x2 2y2 2 2m 1 故y  y  ，y y  1 2 m2 2 1 2 m2 2 1 2m 2m2 因而x x 2y y (my 1)(my 1)2y y (m22) m 1 . 1 2 1 2 1 2 1 2 m2 2 m2 2 m2 2 m2 代入（*）式，得22 22 4 2 , m2 2 m2 因而2 2 12  2，（等号当且仅当时成立） m2 2 m2 2 即 （等号当且仅当时成立）. 4 m2 2 所以，的最大值为 . 4 21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分． 已知函数 y  f x 及其导函数 y  fx 的定义域均为D．设x D，曲线 y  f x 在点  x , f x  处的 0 0 0 切线交x轴于点 x ,0 ．当n1时，设曲线y  f x 在点  x , f x  处的切线交x轴于点 x ,0 ．依此类推， 1 n n n1 称得到的数列 x  为函数 y  f x 关于x 的“N 数列”． n 0 1 （1）若 f xlnx， x  是函数 y  f x 关于x  的“N 数列”，求x 的值； n 0 e 1 x 2 （2）若 f x x2 4， x  是函数 y  f x 关于x 3的“N 数列”，记a log n ，证明： a  是 n 0 n 3 x 2 n n等比数列，并求出其公比； x （3）若 f x ，则对任意给定的非零实数a，是否存在x 0，使得函数 y  f x 关于x 的“N 数 ax2 0 0 列” x  为周期数列？若存在，求出所有满足条件的x ；若不存在，请说明理由． n 0 2 【答案】：（1） ；（2）证明见详解，公比为2；（3）当a<0时，不存在x ,使得x 为周期数列； e 0 n 3a 当a>0时，当且仅当x =± 时，函数 y f x关于x 的“N 数列”x 为周期数列，且周期T =2. 0 3 0 n 1 1 【详解】：（1）曲线y=lnx在点x ,lnx 处的切线斜率为 ，又ln 1 0 0 x e 0 1 1 故曲线y=lnx在点ç çç ,-1÷ ÷ ÷ 处的切线方程为 y+1=eç çç x- ÷ ÷ ÷ ， e e 2 令 y0，得x= . e 2 所以x = . 1 e （2）由题，y f x在x 处的切线方程为y f x  fx xx  n n n n f x  x 24 令 y0，可得x x  n ，即x  n . n1 n fx  n1 2x n n x 2 x 22 a 故 n1  n ，即 n+1 =2. x 2 x 22 a n1 n n 13 又x  ，故a log 25. 1 6 1 3 因此a 是以log 25为首项，2为公比的等比数列. n 3 ax2 （3）由题， fx ，  ax22 故以 ç ç çç x 0 , a+ x 0 x 2 ÷ ÷ ÷ ÷ 为切点的切线方程为 y a x 0 x2   a a   x x 0 2 2 2 xx 0  . 0 0 0 2x 3 令 y=0,可得到x = 0 . 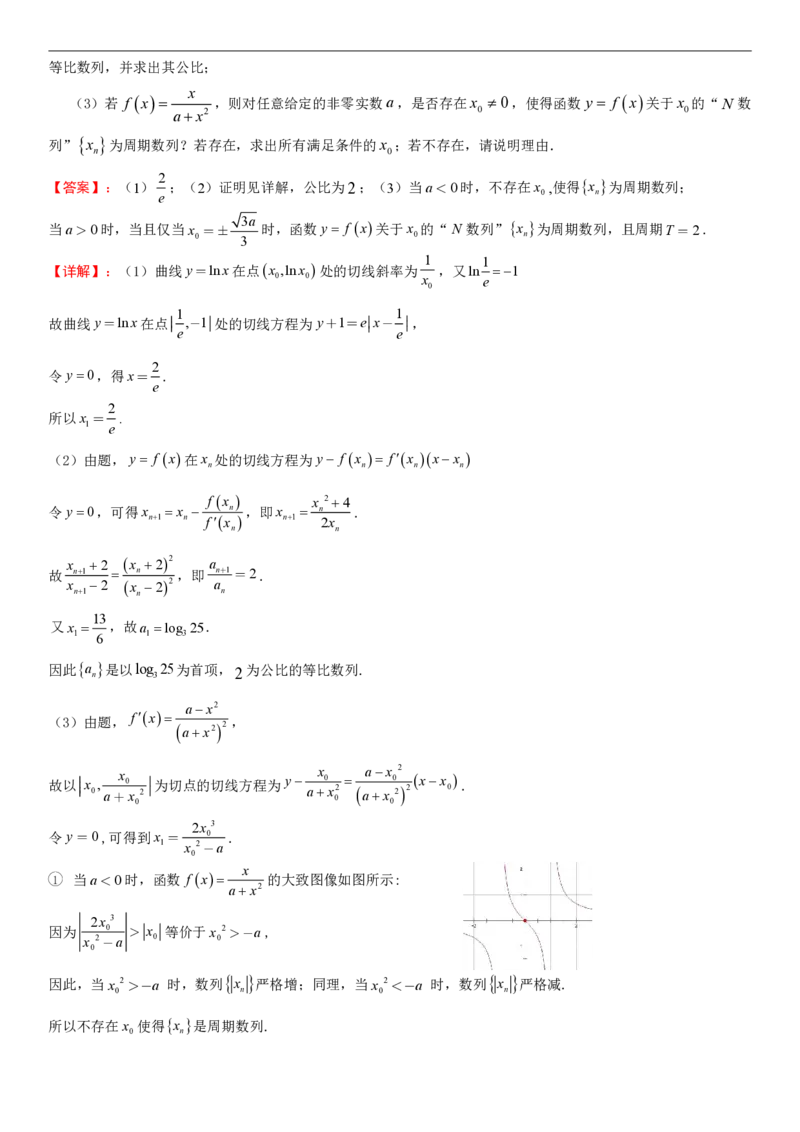1 x 2-a 0 x 1 当a<0时，函数 f x 的大致图像如图所示: ax2 2x 3 因为 0 > x 等价于x 2>-a , x 2-a 0 0 0 因此，当x 2>-a 时，数列 x  严格增；同理，当x 2<-a 时，数列 x  严格减. 0 n 0 n 所以不存在x 使得x 是周期数列. 0 nx ② 当a>0时，函数 f x 的大致图像如图所示: ax2 2x 3 a 令x =-x ,可得 0 =-x ，即x 2= . 1 0 x 2-a 0 0 3 0 依此类推，显然可得x =-x ，…，x =-x . 2 1 n n-1 3a 所以，当x =± 时，数列x 为周期数列，且周期T =2. 0 3 n 下证唯一性： a 2x 3 2x 2 2x 2 当x 2 < 时， 0 = 0 x = 0 x < x ； 0 3 x 2-a x 2-a 0 a-x 2 0 0 0 0 0 因此,数列 x  严格减； n a 2x 2 2a 当x 2 > 时， 0 2 ,12,， 0 3 x 2a x2 a 0 0 2x 3 2x 2 所以 0 = 0 x > x ， x 2 -a x 2 -a 0 0 0 0 因此数列 x  严格增. n 综上,当a<0时，不存在x ,使得x 为周期数列； 0 n 3a 当a>0时，当且仅当x =± 时，函数 y f x关于x 的“N 数列”x 为周期数列，且周期T =2. 0 3 0 n