文档内容
海南省 2023-2024 学年高三学业水平诊断(五)数学
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴
在答题卡上的指定位置.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试
卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知向量 ,若 ,则 ( )
A.-1 B.0 C.1 D.2
2.已知复数 满足 ,则 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知等比数列 的公比不为1,若 ,且 成等差数列,则 ( )
A. B. C. D.
4.在 的展开式中, 的系数为( )
A.30 B.20 C.10 D.-10
5.在 中, 的平分线与对边 交于点 ,若 的面积为 的2倍,且
,则 ( )
A.3 B.4 C.6 D.8
6.在高二选科前,高一某班班主任对该班同学的选科意向进行了调查统计,根据统计数据发现:选物理
的同学占全班同学的80%,同时选物理和化学的同学占全班同学的60%,且该班同学选物理和选化学相互
独立.现从该班级中随机抽取一名同学,则该同学既不选物理也不选化学的概率为( )
A.0.125 B.0.1 C.0.075 D.0.05
7.如图,在直三棱柱 中,点D,E分别在棱 上,
,点 满足 ,若 平面 ,则 的值为( )
学科网(北京)股份有限公司A. B. C. D.
8.在平面直角坐标系 中,已知双曲线 的左、右焦点分别为 , 为
右支上的一点,满足 ,以点 为圆心、 为半径的圆与线段 相交于A,B两点,且
,则 的离心率为( )
A. B. C.2 D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符
合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.若正实数a,b满足 ,则( )
A. 的最小值为 B. 的最大值为1
C. 的最小值为 D. 的取值范围为
10.已知抛物线 的焦点为F,C上一点 到 和到 轴的距离分别为12和10,且点
位于第一象限,以线段 为直径的圆记为 ,则下列说法正确的是( )
A.
B. 的准线方程为
C.圆 的标准方程为
D.若过点 ,且与直线 为坐标原点)平行的直线 与圆 相交于A,B两点,则
学科网(北京)股份有限公司11.在四面体 中, 都是边长为6的正三角形,棱 与平面 所成角的余弦值
为 ,球 与该四面体各棱都相切,则( )
A.四面体 为正四面体
B.四面体 的外接球的体积为
C.球 的表面积为
D.球 被四面体 的表面所截得的各截面圆的周长之和为
三、填空题:本题共3小题,每小题5分,共15分.
12.若定义在 上的奇函数 满足:当 时, ,则 ______.
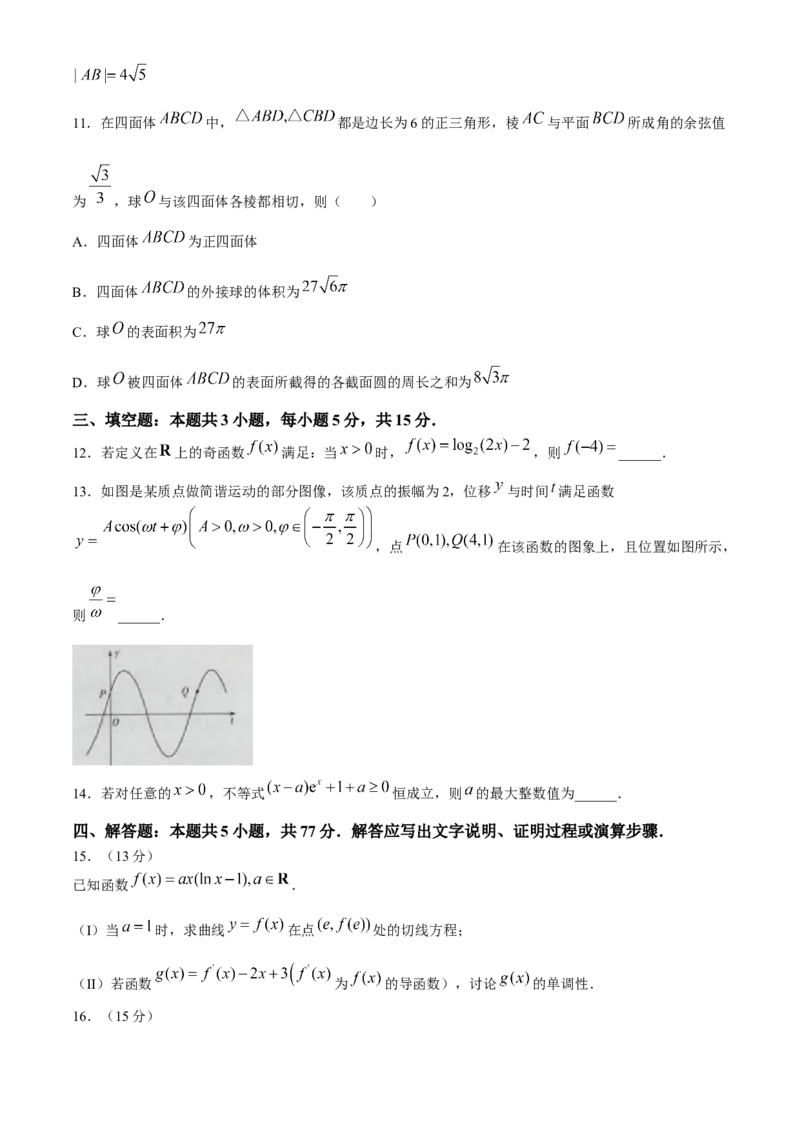
13.如图是某质点做简谐运动的部分图像,该质点的振幅为2,位移 与时间 满足函数
,点 在该函数的图象上,且位置如图所示,
则 ______.
14.若对任意的 ,不等式 恒成立,则 的最大整数值为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知函数 .
(I)当 时,求曲线 在点 处的切线方程;
(II)若函数 为 的导函数),讨论 的单调性.
16.(15分)
学科网(北京)股份有限公司某大型公司进行了新员工的招聘,共有来自全国各地的10000人参加应聘.招聘分为初试与复试.初试为
笔试,已知应聘者的初试成绩 .复试为闯关制:共有三关,前两关中的每一关最多可闯两
次,只要有一次通过,就进入下一关,否则闯关失败;第三关必须一次性通过,否则闯关失败.若初试通
过后,复试三关也都通过,则应聘成功.
(I)估计10000名应聘者中初试成绩位于区间 内的人数;
(II)若小王已通过初试,在复试时每次通过第一关、第二关及第三关的概率分别为 , ,且每次闯
关是否通过不受前面闯关情况的影响,求小王应聘成功的概率 .
附:若随机变量 ,则
.
17.(15分)
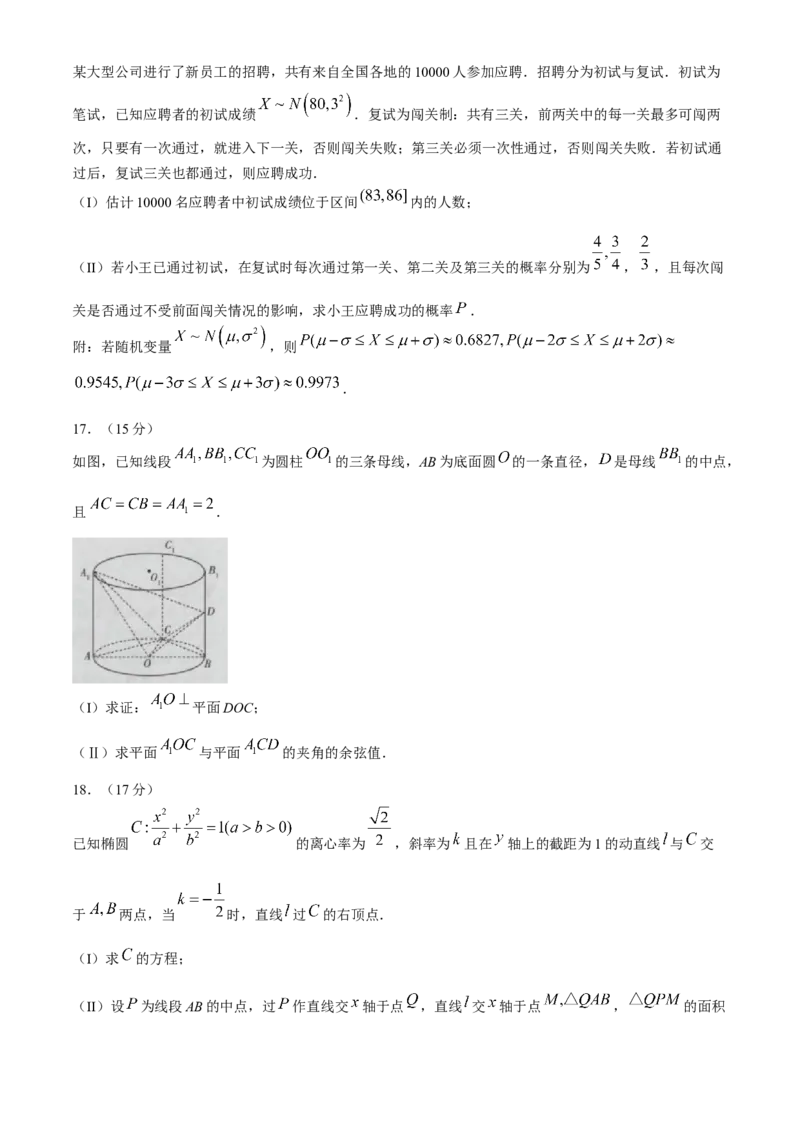
如图,已知线段 为圆柱 的三条母线,AB为底面圆 的一条直径, 是母线 的中点,
且 .
(I)求证: 平面DOC;
(Ⅱ)求平面 与平面 的夹角的余弦值.
18.(17分)
已知椭圆 的离心率为 ,斜率为 且在 轴上的截距为1的动直线 与 交
于 两点,当 时,直线 过 的右顶点.
(I)求 的方程;
(II)设 为线段AB的中点,过 作直线交 轴于点 ,直线 交 轴于点 , 的面积
学科网(北京)股份有限公司分别记为 ,若 ,求 的取值范围.
19.(17分)
已知数列 的各项均为正整数,记集合 的元素个数为 .
(I)若 为1,2,3,6,写出集合 ,并求 的值;
(II)若 为1,3,a,b,且 ,求 和集合 ;
(III)若 是递增数列,且项数为 ,证明:“ ”的充要条件是“ 为等比数列”.
学科网(北京)股份有限公司海南省 2023~2024 学年高三学业水平诊断(五)
数学・答案
一、单项选择题:本题共8小题,每小题5分,共40分.
1.B 2.A 3.C 4.C 5.A 6.D 7.C 8.D
二、多项选择题:本题共3小题,每小题6分,共18分.每小题全部选对的得6分,部分选
对的得部分分,有选错的得0分.
9.BC 10.ACD 11.ABD
三、填空题:本题共3小题,每小题5分,共15分.
12.-1 13. 14.2
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.解析(I)当 时, ,所以 ,
所以 ,
所以曲线 在点 处的切线方程为 ,即 .
(II)因为 ,所以 ,
所以 ,所以 .
①若 ,则 ,所以 在 上单调递减;
②若 ,则当 时, ,所以 在 上单调递增,当 时,
,所以 在 上单调递减.综上,当 时, 在 上单调递减;当
时, 在 上单调递增,在 上单调递减.
16.解析(I)因为 ,
所以 .
学科网(北京)股份有限公司因为 ,所以 ,
估计10000名应聘者中初试成绩位于 内的人数为 .
(II)设复试时小王通过第一关的概率为 ,通过第二关的概率为 ,通过第三关的概率为 .
由题意可得 ,
所以小王应聘成功的概率 .
17.解析(I)连接 .因为 为底面圆 的直径,所以 为 的中点, .
又因为 ,所以 .
由圆柱的性质知 平面 ,而 平面 ,所以 .
又 ,且 平面 ,所以 平面 .
因为 平面 ,所以 .
因为 为母线 的中点,
所以
,所以 ,则 .
又 平面 ,且 ,所以 平面 .
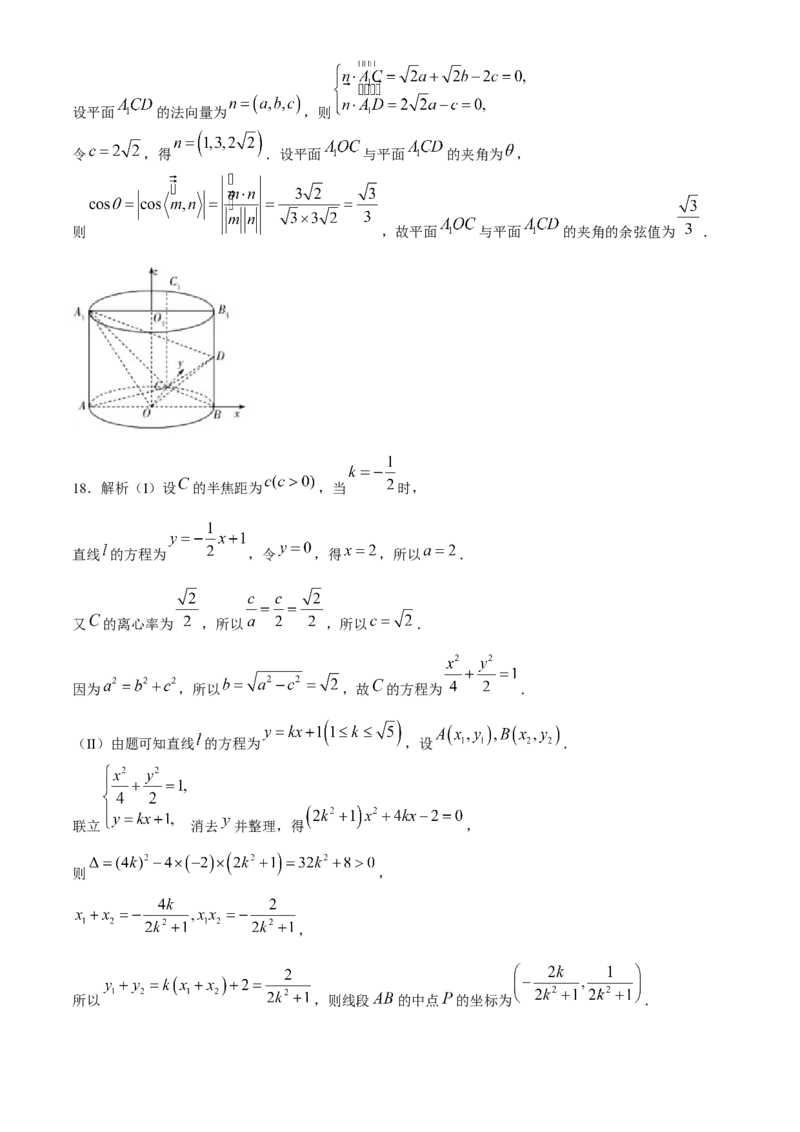
(II)连接 ,易知 平面 ,所以以 为坐标原点,
以 所在直线分别为 轴建立如图所示的空间直角坐标系 ,
则 ,
所以 .
设平面 的法向量为 ,
则 令 ,得 .
学科网(北京)股份有限公司设平面 的法向量为 ,则
令 ,得 .设平面 与平面 的夹角为 ,
则 ,故平面 与平面 的夹角的余弦值为 .
18.解析(I)设 的半焦距为 ,当 时,
直线 的方程为 ,令 ,得 ,所以 .
又 的离心率为 ,所以 ,所以 .
因为 ,所以 ,故 的方程为 .
(II)由题可知直线 的方程为 ,设 .
联立 消去 并整理,得 ,
则 ,
,
所以 ,则线段 的中点 的坐标为 .
学科网(北京)股份有限公司对于直线 ,令 ,可得 ,
所以 ,
所以 .
令 ,则 ,
而 ,所以 在 上单调递增,所以 ,
故 的取值范围为 .
19.解析(I)因为 ,
所以集合 .
(II)因为 为 ,且 ,所以 互不相等,
所以 都是集合 中的元素.因为 ,所以 ,解得 ,
所以 为 ,所以 .
(III)充分性:若 是递增的等比数列,设 的公比为 ,当 时, ,
所以 ,且 ,故充分性成立.
学科网(北京)股份有限公司必要性:若 是递增数列,且 ,则 ,
所以 ,且互不相等,又因为 ,
所以 ,且 互不相等,
所以 ,所以 ,
所以 ,所以 为等比数列,故必要性成立.
综上,“ ”的充要条件是“ 为等比数列”.
学科网(北京)股份有限公司