文档内容
2024年9月
绵阳南山中学2024年秋高2022级高三上9月月考试题
数 学
命题人:张韬 审题人:雍华 赵立信
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.)
1.若集合 , ,则 ( )
A. B.
C. D.
2.若命题 : , ,则命题 的否定是( )
A. , B. ,
C. , D. ,
3.若 ,则下列不等式一定成立的是( )
A. B.
C. D.
4.记等差数列 的前n项和为 ,若 , ,则 ( )
A.49 B.63 C.70 D.126
5.已知函数 为偶函数,则 ( )
A. B. C. D.6.已知把物体放在空气中冷却时,若物体原来的温度是 ,空气的温度是 ,则
后物体的温度 满足公式 (其中 是一个随着物体与空气的接触状况
而定的正常数).某天小明同学将温度是 的牛奶放在 空气中,冷却 后牛奶的
温度是 ,则下列说法正确的是( )
A. B.牛奶的温度从50 降至 还需
C. D.牛奶的温度从50 降至 还需
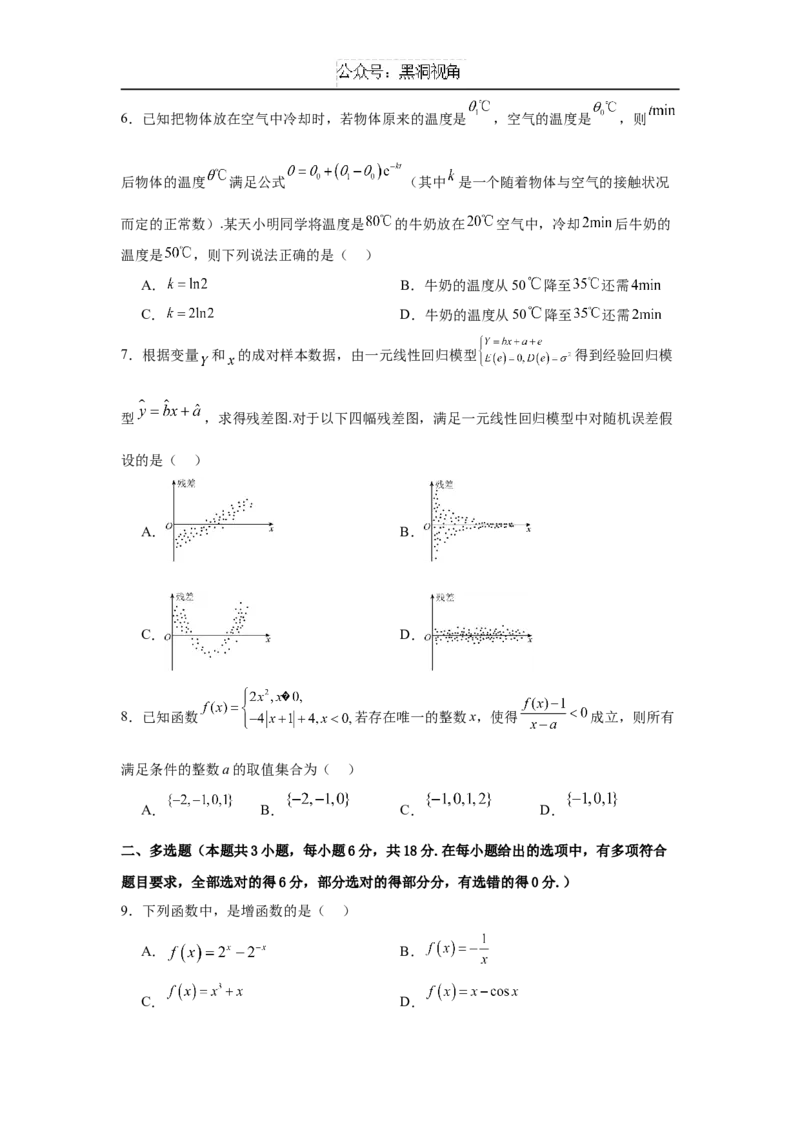
7.根据变量 和 的成对样本数据,由一元线性回归模型 得到经验回归模
型 ,求得残差图.对于以下四幅残差图,满足一元线性回归模型中对随机误差假
设的是( )
A. B.
C. D.
8.已知函数 若存在唯一的整数x,使得 成立,则所有
满足条件的整数a的取值集合为( )
A. B. C. D.
二、多选题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.)
9.下列函数中,是增函数的是( )
A. B.
C. D.10.某制药公司为了研究某种治疗高血压的药物在饭前和饭后服用的药效差异,随机抽取
了200名高血压患者开展试验,其中100名患者饭前服药,另外100名患者饭后服药,随
后观察药效,将试验数据绘制成如图所示的等高条形图,已知
,且 ,
则下列说法正确的是( )
A.饭前服药的患者中,药效强的频率为
B.药效弱的患者中,饭后服药的频率为
C.在犯错误的概率不超过0.01的条件下,可以认为这种药物饭前和饭后服用的药效有
差异
D.在犯错误的概率不超过0.01的条件下,不能认为这种药物饭前和饭后服用的药效有
差异
11.已知函数 ( )是奇函数, 是 的导函数( ), 且
有 满足 ,则下列说法正确的是( )
A. B.函数 为偶函数
C. D.函数 的周期为4
三、填空题(本题共3小题,每小题5分,共15分.把答案填在题中的横线上.)
12.若 , ,则 .
13.函数 的所有零点的和等于 .14.对任意的 ,不等式 恒成立,则实数
= .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.)
15.(13分) 中,内角 的对边分别为 ,且 .
(1)若 ,求 ;
(2)若 的面积为 ,求 .
16.(15分)在数列 中, 是其前 项和,且 .
(1)求数列 的通项公式;
(2)若 , 恒成立,求 的取值范围.
17.(15分)某生物兴趣小组研究某种植物的生长,每天测量幼苗的高度,设其中一株幼
苗从观察之日起,第 天的高度为 ,测得一些数据图如下表所示:
第 天 1 2 3 4 5
高度 1.3 1.7 2.2 2.8 3.5
(1)由表中数据可看出,可用线性回归模型拟合 与 的关系,请用相关系数加以证明;
(2)求 关于 的回归直线方程,并预测第7天这株幼苗的高度.
参考数据: .
参考公式:相关系数 ,回归方程 中斜率和截距的最小二乘估计公式分别为 .
18.(17分)函数 .
(1)若 1,求函数 在 处的切线方程;
(2)证明:存在实数 使得曲线 关于点 成中心对称图形;
(3)讨论函数 零点的个数.
19.(17分)已知 .
(1)当 时,求 的单调递增区间;
(2)若 有两个极值点 , .
(i)求 的取值范围;
(ii)证明: .