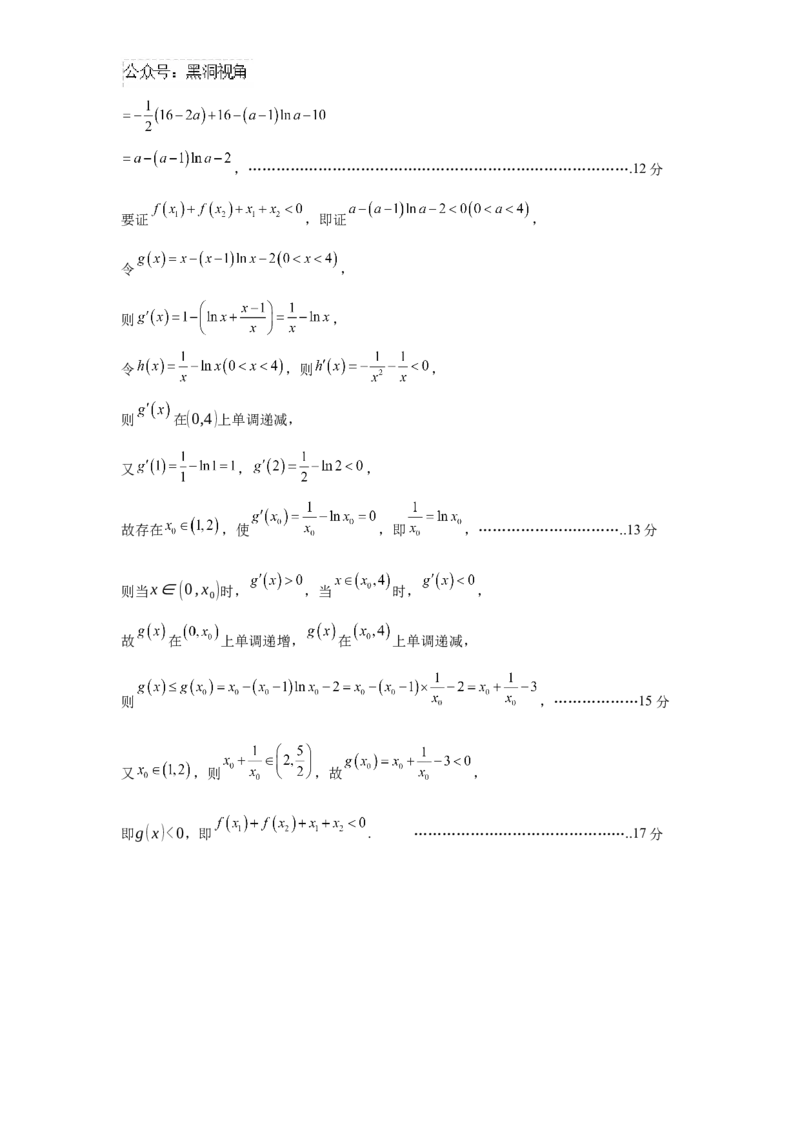文档内容
绵阳南山中学2024年秋高2022级高三上9月月考
数学参考答案及评分标准
一、 单选题
题号 1 2 3 4 5 6 7 8
答案 C C B B C D D A
二、 多选题
题号 9 10 11
答案 ACD AC ABD
三、 填空题
12、 13、 0 14、
四、解答题
15.
(1)由余弦定理知
…………………………………………………….……..3分
又 故 ; ……………………………………………………….…..6分
(2)由三角形的面积公式
从而 , …………………………………….……..8分
若 , , ……………10分
若 , , …12分
从而 …………………………………..13分
16.(1)因为 ,
当 时, ,解得 ;………………………………………………...2分当 时, ,所以 ,所以 ;………4分
所以{a }是以 为首项, 为公比的等比数列,
n
所以 . …………………………………………………………………….6分
(2)由(1)可得 ,
又 在 上单调递减,则 在 上单调递增,
所以当 为偶数时, ,
当 为奇数时, ,………………………………………10分
所以当 时 取得最大值为 ,当 时 取得最小值为 ,
因为 , 恒成立,
所以 ,解得 ,………………………………………………… …...14分
所以 的取值范围为 . …………………………………………………………...15分
17.(1)由 , ,
,
……………………… …….3分所以
……………………………………....7分
因为 与1非常接近,故可用线性回归模型拟合 与 的关系.
(2)由题意可得: ,….11分
所以 关于 的回归直线方程为 .
………………………………………….…………..13分
当 时, ,
由此预测当年份序号为第7天这株幼苗的高度为4.5 ……………………………..…15分
18. (1)
………………………………………………………………..….2分
故 在 处的切线方程为 ,即 …………………4分
(2) ,若存在这样的 ,使得 为 的对称中心,
则 , …………………………………………………….……6分
现在只需证明当 时 ,事实上,
于是 ………………………………………………………………….8分
即存在实数 使得 是 的对称中心. ………………………………………. .9分(3) ,
3.1)当 时,
时 ,故 在 上单调递增,
时, , 单调递减, ………………………………………………..10分
则 在 处取到极大值,在 处取到极小值,
由 ,而 ,根据零点存在定理 在 上有一个零点;
i)若 ,即 , 在 无零点,从而 在 上有1个
零点;
………………………………………………………….11分
ii)若 ,即 , , 在 有一个零点,
,故 在 有一个零点,从而 在 上
有3个零点;
……………………………………………………………12分
iii)若 ,即 , 在 有一个零点,从而 在 上有2个
零点;
……………………………………………………………..13分
3.2)当 时, 在 上单调递增, , 时, ,从
而 在 上有一个零点; …………………………………………………….....14分
3.3)当 时, 时 ,故 在 上单调
递增, 时, , 单调递减. ………………………….15分而 , ,故 在 无零点,又
,由 ,故 ,
,从而 在 有一个零点,从而 在 上有一个零点.
………………………………………………..…..16分
综上:当 时, 在 上只有1个零点; 时, 在 上有2个零点;
时 在 上有3个零点。
…………………………………..17分
19.(1)当 时, ,
, ……………………………….……………..2 分
当 ,即 时,f'(x)>0,
故 单调递增区间为 ; ………………………………………………………4分
(2) ,令 ,即 ,
令 , ,则 、 是方程 的两个正根,……………………...6分
则 ,即 , ………………………..…8分
有 , ,即 ,………………………………………...……..10分
(3),……………………………………………………………………….12分
要证 ,即证 ,
令 ,
则 ,
令 ,则 ,
则 在(0,4)上单调递减,
又 , ,
故存在 ,使 ,即 ,…………………………..13分
则当x∈(0,x )时, ,当 时, ,
0
故 在 上单调递增, 在 上单调递减,
则 ,………………15分
又 ,则 ,故 ,
即g(x)<0,即 . ………………………………………..17分