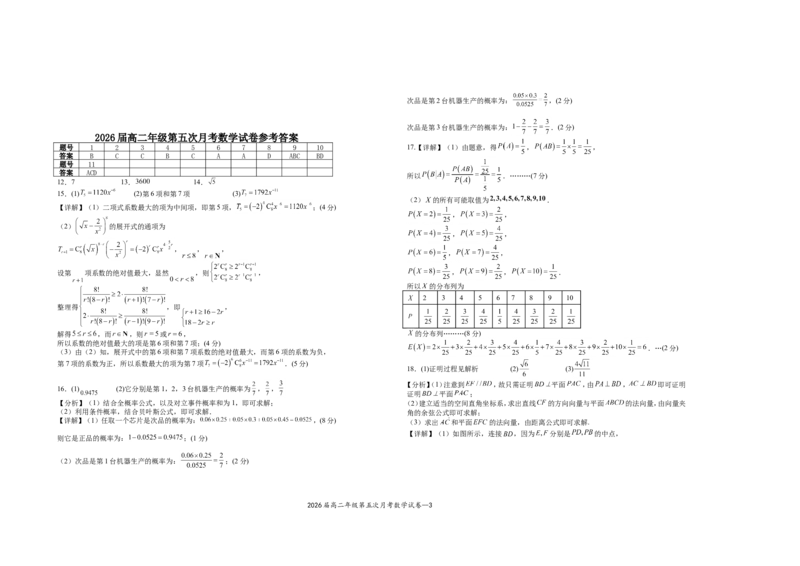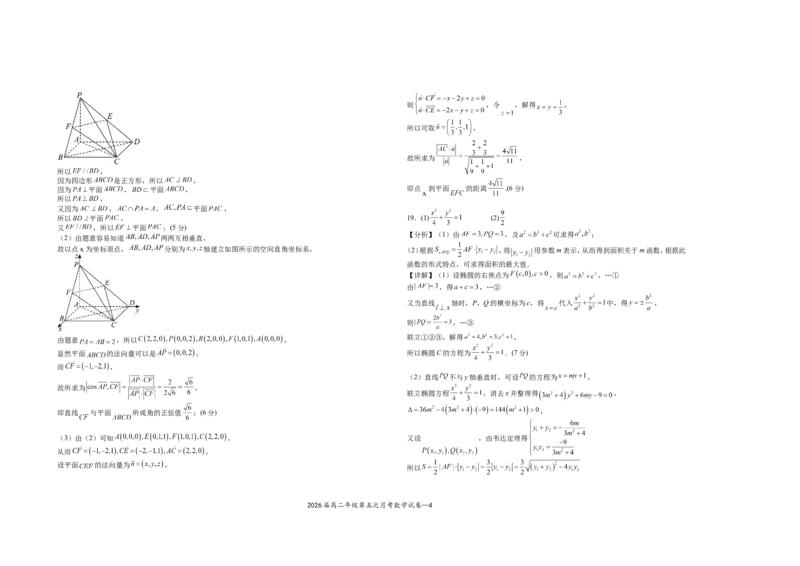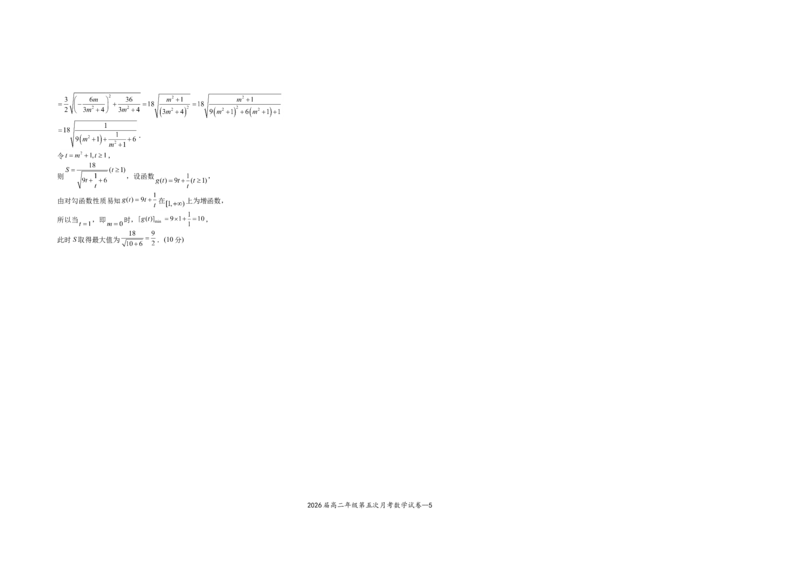文档内容
2026届高二年级第五次月考数学试卷 D.一瓶净含量为 的果汁的容量
一、单选题 10.已知离散型随机变量 的分布列如表所示,若离散型随机变量 满足 ,则
1.直线 被圆 截得的弦长为( ) ( )
A.1 B.2 C.3 D.4 1 2 3 4
2.已知随机变量 的分布列为 ,2,3, , ,则 ( ) 0.5 0.3 0.1
A. B.
A. B. C. D.
C. D.
3.若 ,则 的值为( )
11.如图,在棱长为2的正方体 中,点O为BD的中点,且点P满足
A.14 B.84 C.34 D.204
,则下列说法正确的是( )
4.6名同学到 三个场馆做志愿者,每名同学只去1个场馆,A场馆安排1名,B场馆安
排2名,C场馆安排3名,则不同的安排方法的个数有( )
A.30 B.60 C.120 D.360
5.已知今天是星期日,则经过 天后是( )
A.星期一 B.星期二 C.星期三 D.星期四
6.若 ,则 ( )
A.180 B. C. D.90
7.质数(prime number)又称素数,一个大于1的自然数,除了1和它本身外,不能被其他自然
数整除,则这个数为质数.数学上把相差为2的两个素数叫做“孪生素数”.如:3和5,5和
A.若 ,则
7,…,那么,如果我们在不超过32的自然数中,随机选取两个不同的数,记事件A=“这两
个数都是素数”,事件B=“这两个数不是孪生素数”,则 ( ) B.若 , ,则点P的轨迹长度为
A. B. C. D.
C.若 , ,则
8.如图所示的为太极八卦图,八卦分据八方,中绘太极,古代常用此图作为除凶避灾的吉祥
图案.八卦中的每一卦均由纵向排列的三个爻组成,其中“ ”为阳爻,“ ”为阴爻.
D.若 , ,直线OP与平面 所成的角为 ,则
现从八卦中任取两卦,已知取出的两卦中有一卦恰有一个阳爻,则另一卦至少有两个阳爻的
概率为( )
三、填空题
12.计算: .
13. 名男生、 名女生站成一排,至少有两个女生相邻的站法种数为(用数字作答) .
14.已知双曲线 左、右焦点分别为 , ,过点 作渐近线的垂线,
垂足为 ,交右支于点 ,若 ,则 的离心率是 .
四、解答题
A. B. C. D.
15.在 的展开式中.
二、多选题
(1)求二项式系数最大的项;
9.下列变量中,是离散型随机变量的是( ).
(2)系数的绝对值最大的项是第几项?
A.某机场明年5月1日运送乘客的数量
(3)求系数最大的项.
B.某办公室一天中接到电话的次数
C.某地警方明年5月1日到10月1日期间查处酒驾司机的人数
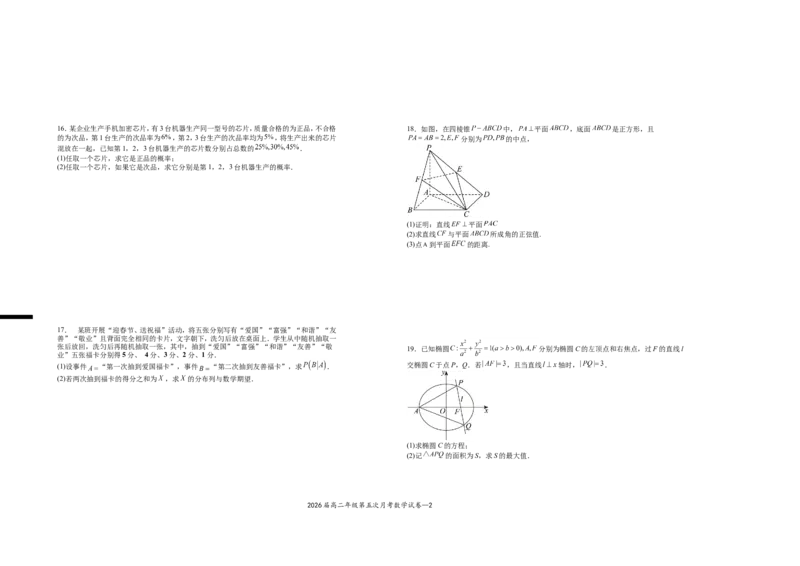
2026届高二年级第五次月考数学试卷--116.某企业生产手机加密芯片,有3台机器生产同一型号的芯片,质量合格的为正品,不合格 18.如图,在四棱锥 中, 平面 ,底面 是正方形,且
的为次品,第1台生产的次品率为 ,第2,3台生产的次品率均为 ,将生产出来的芯片 分别为 的中点,
混放在一起,已知第1,2,3台机器生产的芯片数分别占总数的 .
(1)任取一个芯片,求它是正品的概率;
(2)任取一个芯片,如果它是次品,求它分别是第1,2,3台机器生产的概率.
(1)证明:直线 平面
(2)求直线 与平面 所成角的正弦值.
(3)点 到平面 的距离.
17. 某班开展“迎春节、送祝福”活动,将五张分别写有“爱国”“富强”“和谐”“友
善”“敬业”且背面完全相同的卡片,文字朝下,洗匀后放在桌面上.学生从中随机抽取一
张后放回,洗匀后再随机抽取一张,其中,抽到“爱国”“富强”“和谐”“友善”“敬
19.已知椭圆 分别为椭圆C的左顶点和右焦点,过F的直线l
业”五张福卡分别得5分、 4分、3分、2分、1分.
(1)设事件 “第一次抽到爱国福卡”,事件 “第二次抽到友善福卡”,求 . 交椭圆C于点P,Q.若 ,且当直线 轴时, .
(2)若两次抽到福卡的得分之和为 ,求 的分布列与数学期望.
(1)求椭圆C的方程;
(2)记 的面积为S,求S的最大值.
2026届高二年级第五次月考数学试卷--2次品是第2台机器生产的概率为: ,(2分)
次品是第3台机器生产的概率为: .(2分)
2026届高二年级第五次月考数学试卷参考答案
题号 1 2 3 4 5 6 7 8 9 10 17.【详解】(1)由题意,得 , ,
答案 B C C B C A A D ABC BD
题号 11
答案 ACD
所以 .………(7分)
12.7 13. 14.
15.(1) (2)第6项和第7项 (3)
(2) 的所有可能取值为 .
【详解】(1)二项式系数最大的项为中间项,即第5项, ;(4分)
, ,
(2) 的展开式的通项为
, ,
, , ,
, ,
设第 项系数的绝对值最大,显然 ,则 , , , .
所以 的分布列为
2 3 4 5 6 7 8 9 10
整理得 ,即 ,
解得 ,而 ,则 或 , 的分布列………(8分)
所以系数的绝对值最大的项是第6项和第7项;(4分)
.…(2分)
(3)由(2)知,展开式中的第6项和第7项系数的绝对值最大,而第6项的系数为负,
第7项的系数为正,所以系数最大的项为第7项 .(5分)
18.(1)证明过程见解析 (2) (3)
【分析】(1)注意到 ,故只需证明 平面 ,由 , 即可证明
16.(1) (2)它分别是第1,2,3台机器生产的概率为 , ,
证明 平面 ;
【分析】(1)结合全概率公式,以及对立事件概率和为1,即可求解; (2)建立适当的空间直角坐标系,求出直线 的方向向量与平面 的法向量,由向量夹
(2)利用条件概率,结合贝叶斯公式,即可求解. 角的余弦公式即可求解;
【详解】(1)任取一个芯片是次品的概率为: ,(8分) (3)求出 和平面 的法向量,由距离公式即可求解.
【详解】(1)如图所示,连接 ,因为 分别是 的中点,
则它是正品的概率为: ;(1分)
(2)次品是第1台机器生产的概率为: ;(2分)
2026届高二年级第五次月考数学试卷--3则 ,令 ,解得 ,
所以可取 ,
故所求为 ,
所以 ,
因为四边形 是正方形,所以 ,
因为 平面 , 平面 , 即点 到平面 的距离 .(6分)
所以 ,
又因为 , , 平面 ,
所以 平面 , 19.(1) (2)
又 ,所以 平面 ;(5分)
【分析】(1)由 ,及 可求得 ;
(2)由题意容易知道 两两互相垂直,
故以点 为坐标原点, 分别为 轴建立如图所示的空间直角坐标系, (2)根据 ,将 用参数m表示,从而得到面积关于m函数,根据此
函数的形式特点,可求得面积的最大值.
【详解】(1)设椭圆的右焦点为 ,则 ,…①
由 ,得 ,…②
又当直线 轴时,P,Q的横坐标为c,将 代入 中,得 ,
则 ,…③
联立①②③,解得 ,
由题意 ,所以 ,
显然平面 的法向量可以是 , 所以椭圆C的方程为 .(7分)
而 ,
(2)直线 不与y轴垂直时,可设 的方程为 ,
故所求为 ,
联立椭圆方程 ,消去x并整理得 ,
即直线 与平面 所成角的正弦值 ;(6分) ,
(3)由(2)可知 , 又设 ,由韦达定理得
从而 ,
设平面 的法向量为 ,
所以
2026届高二年级第五次月考数学试卷--4.
令 ,
则 ,设函数 ,
由对勾函数性质易知 在 上为增函数,
所以当 ,即 时, ,
此时S取得最大值为 .(10分)
2026届高二年级第五次月考数学试卷--5