2023年11月模拟答案(1)_2023年11月_0211月合集_2024届河北省石家庄市高三上学期教学质量摸底检测_2024届河北省石家庄市普通高中学校毕业年级教学质量摸底检测数学试卷

石家庄市 2024 届高中毕业年级教学质量摸底检测
（数学答案）
（一、二）选择题
1 2 3 4 5 6 7 8 9 10 11 12
B A C B C D A D ABD BD BCD AC
（三）填空题
13.  1 6 0 14. 2 3
15. 18 16.
1
x
2
2
2 5

1
y
4
2
4
 1 ， y 2  2 9 2  x  3 6 
（四）解答题（阅卷过程中发现的其他解法参照本答案的评分细则，教研组研讨决定）
17. 【解析】(1)设等差数列的公差为d，
a 5
由 3 ,可得
S 64
 8

a
8
1
a

1

2 d
8


2
7
5
d  6 4
…...................……….......……………………2分
解得
 a
d
1


1
2
， …...................……….......…………………….4分
所以a 2n1， ………………………….......…………………….5分
n
(2)因为
a
n
1
a
n  1
=
( 2 n  1
1
) ( 2 n  1 )

1
2
(
2 n
1
 1

2 n
1
 1
) ，
所以 T
n
=
1
2
(1 
1
3

1
3

1
5

1
5

1
7
    
2 n
1
 1

2 n
1
 1
) ………………………......………………………7分
=
1
2
(1 
2 n
1
 1
) ………………………………………………....…………………9分
因为 n  N * ，所以
1
2
(1 
2 n
1
 1
) 
1
2
，即 T
n
<
1
2
.……………………......………………………10分
18. 【解析】(1)由余弦定理可得：
AC2 b2 a2 c2 2accosB1612242 3cos15052，
则 A C  2 13， …………………………..........…………………2分
a b 2 3 2 13
又因为  ，即  …………………………..........…………………4分
sin A sinB sin A sin150
{#{QQABKQKEogAoQABAABhCEwVyCgKQkAGACCoOxBAEIAAAARFABCA=}#}所以 s in  B A C 
2
3
6
9
. ………………………….........…………………5分
（2）因为 s in  B A C 
2
3
6
9
，所以 c o s  B A C 
7
2
1
6
3
，
从而 t a n  B A C 
7
3
， ……………………………...........……………........…7分
在RtABD中， B D  A B  t a n  B A C  4 
7
3

4
7
3
……………………………..…......……...……9分
 S
 B C D

1
2
B D  B C  s i n  D B C
1 4 3 3
   …...........……………………….......…......…11分
2 7 2
 S
 B C D

6
7
3
……................……………………….......…......…12分
19.【解析】（1）因为 P C  平面 A B C ， A C  平面 A B C ，所以 P C  A C , 又 P C  4 ， P A  2 6 ，
所以AC 2 2. ......................................................................……………………………...................….......2分
在ABC中，因为 A B  B C  2 ，所以 A B 2  B C 2  A C 2 ，所以 A B  B C
因为 P C  平面 A B C ， A B  平面ABC，所以 P C  A B ， ..………........…….........……........4分
又因为 P C B C  C ，
所以 A B  平面 P B C ． .................................……………...................................5分
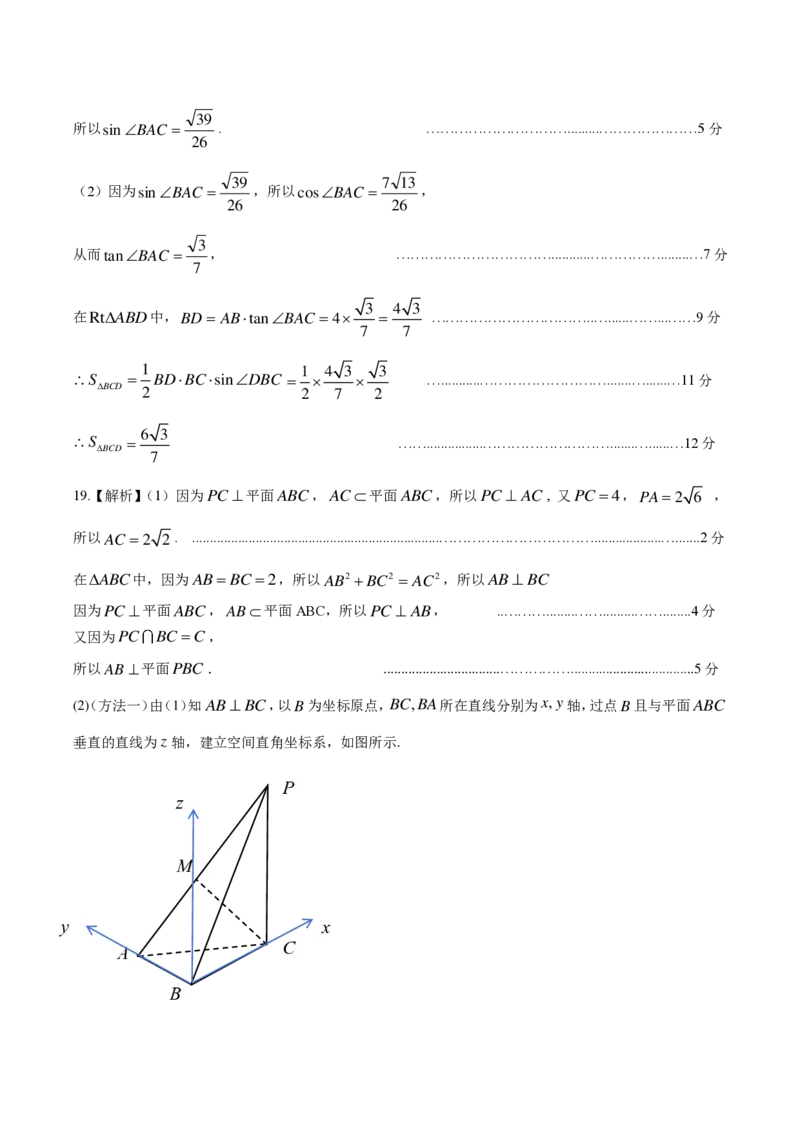
(2（) 方法一）由（1）知 A B  B C ，以 B 为坐标原点， B C , B A 所在直线分别为x,y轴，过点 B 且与平面 A B C
垂直的直线为 z 轴，建立空间直角坐标系，如图所示.
P
z
M
y x
C
A
B
{#{QQABKQKEogAoQABAABhCEwVyCgKQkAGACCoOxBAEIAAAARFABCA=}#}则 B  0 , 0 , 0  , A  0 , 2 , 0  , P  2 , 0 , 4  , C  2 , 0 , 0  ， M  1 , 1 , 2  ，
所以 C M    1 , 1 , 2  ， B A   0 , 2 , 0  ， B P   2 , 0 , 4  ..................……………........................... 6分
设平面 P A B 的法向量为 n   x , y , z  ，则
 n
n


B
B
A
P


0
0
，即
 2
2
y
x


0
4 z  0
，
令 x  2 ，则z 1，所以 n   2 , 0 ,  1  ， .........................……………................................... 8分
设 C M 与平面 P A B 所成角为，
CM n 22 2 30
cos CM,n   
则 ， .......................................................................10分
CM n 6 5 15
s i n c o s C M , n
2
1
3
5
0
   ， c o s
1
1
0
5
5
  
即 C M 与平面 P A B 所成角的余弦值为
1
1
0
5
5
．.............................................................................12分
（2）（方法二）过点 C 作 C N  P B ，垂足为 N ，连接 M N ， ......................................................6分
由（1）知AB 平面 P B C ， A B  平面 P A B ，  平面 P A B  平面 P B C ，
平面PAB 平面 P B C  P B ，CN 平面 P B C ， C N  P B ，
 CN 平面 P A B ，
CMN 为CM 与平面 P A B 所成角， ..........................................8分
1
在RtPAC中，CM  PA 6，
2
PCBC 42 4 5
在RtPBC中，CN    ，...........................................................................10分
PB 2 5 5
 在 R t  C M N
2
 2 4 5 70
中，MN  CM2 CN2  6    ，
 
5 5
 
故 c o s  C M N 
M
C
N
M

1
1
0
5
5
，
105
即CM 与平面PAB所成角的余弦值为 . ...............................................................................12分
15
20.【解析】（1）设A“张某选择甲类问题”，B “张某答对所选问题”，
M “张某至少答对一道问题”,
{#{QQABKQKEogAoQABAABhCEwVyCgKQkAGACCoOxBAEIAAAARFABCA=}#}则 A  “张某选择乙类问题”， B  “张某未答对所选问题”
M  “张某一道问题都没答对”. .......................................................................................................1分
由题意得，𝑃（𝐴） = 𝑃（𝐴̅） = 0.5，
P

B A

 0 . 9
     
， P B A 0.1 ，P B A 0.7，P B A 0.3， .....................................2分
由全概率公式，得
P  M   P  A  P  B A   P  A  P  B A   0 .5  0 .1  0 .5  0 .3  0 .2 .........................................................4分
 P  M   1  P  M   1  0 .2  0 .8 . .........................................................................................................5分
（2）根据条件可知：若张某先回答甲类问题，
则张某的累计得分𝑋的可能值为0，30，80， .............................................................................................. 6分
∵张某能正确回答甲类问题的概率为0.9，能正确回答乙类问题的概率为0.7，
 P  X  0   1  0 .9  0 .1 ； P  X  3 0   0 . 9   1  0 . 7   0 . 2 7 ； P  X  8 0   0 . 9  0 . 7  0 . 6 3 ，
则𝑋的分布列为
X 0 30 80
P 0.1 0.27 0.63
当张某先回答甲类问题时，累计得分的期望为
EX00.1300.27800.6358.5，.........................................................................................
8分
若张某先回答乙类问题，则张某的累计得分𝑌的可能值为0，50，80，......................................................9分
同理可求 P  Y  0   1  0 .7  0 .3 ； P  Y  5 0   0 .7   1  0 .9   0 .0 7 ； P  Y  8 0   0 .7  0 .9  0 .6 3 ，
则此时累计得分的期望为 E  Y   0  0 .3  5 0  0 .0 7  8 0  0 .6 3  5 3 .9 ...................................................11分
因为EXEY
，
所以，以累计得分多为决策依据，张某应选择先回答甲类问题． ............................................................12分
21．【解析】(1)设 E 的方程为mx2 ny2 1  m0,n0  ， ..................................................................1分
代入 A
 3
2
,  1
 1 1
和B0,2 两点得m ,n ，........................................................................................2分
3 4
x2 y2
所以E的方程为  1. ..........................................................................................................................4分
3 4
{#{QQABKQKEogAoQABAABhCEwVyCgKQkAGACCoOxBAEIAAAARFABCA=}#}（2）设过点C的直线方程为 y  k x  4 ，
 y
x
3

2

k x
y
4

2
4
 1
消去y得  3 k 2  4  x 2  2 4 k x  3 6  0 ，
24k2 436  3k2 4  144  k2 4  0，解得 k  2 或 k   2 ， ......................................5分
设 M ( x
1
, y
1
) N ( x
2
, y
2
) ，则 x
1
 x
2

3
2
k
4
2
k
 4
， x
1
x
2

3 k
3
2
6
 4
..............................................................6分
设过点M 且斜率为-2的直线为 y  y
1
  2 ( x  x
1
) ，令 y   1 ，
所以 Q (
2 x
1

2
y
1
 1
,  1 ) ， H ( x
1
 y
1
 1 ,  2  y
1
) ，
y  y 2
所以直线NH 的斜率为 1 2 ，
x x  y 1
2 1 1
直线 N H 为 y  y
2

x
2
y
1

x
1
y

2

y
1
2
 1
( x  x
2
) ，..........................................................................................8分
令y1，
x 
(  1  y
2y
) (
1
x

2
y

2
x

1

2
y
1
 1 )
 x
2

y
2
x
1
 y
1
x
2y

1

y
1y
y
2
2

2
x
1
 x
2
 1
 1 ， ①
将 y kx 4，y kx 4代入①式，得
1 1 2 2
2kx x 3(x x ) y y 1 (2kk2)x x (4k3)(x x )15
x 1 2 1 2 1 2 1 1 2 1 2 1，②
y  y 2 k(x x )6
1 2 1 2
..........................................................................................................................................................10分
将 x
1
 x
2

3
2
k
4
2
k
 4
， x
1
x
2

3 k
3
2
6
 4
代入②式，得
36 24k
(2kk2) (4k3)( )15
3k2 4 3k2 4
x
24k2
6
3k2 4

 1
6
5
k
k
2
2


2
6
4
0
 1  
3
2
，
所以直线 H N 与直线 y   1 交点为定点


3
2
,  1

. ............................................................................12分
22．【解析】（1） fxaex1(1a)，...................................................................................................1分
1a
当0a1时，令 fx0，得x1ln ，
a
{#{QQABKQKEogAoQABAABhCEwVyCgKQkAGACCoOxBAEIAAAARFABCA=}#}当 x 

  , 1  l n
1 
a
a 
时， f   x   0 ；当 x 

1  l n
1 
a
a
,  

时， f   x   0 ．
故 f  x 
 1a
在 ,1ln 上单调递减，在
 a 

1  l n
1 
a
a
,  

上单调递增．........................................3分
当 a  1 时， f   x   0 ， f  x  在    ,    上单调递增. ............................................................................4分
（2） g  x   l n x  x 
a e x
x
 1
 1
x1 aex1x 
，x0,，gx ，
x2
显然， 是方程
x1 g   x   0
的一个根.
令 f xaex1x, f(x)aex11, f(x)0的解为
1 1 1
x  1  l n a ，
当1lna0，即ae时， f 1 ( x )  0 ， f
1
 x  在  0 ,    上单调递增，不符合题意，故舍去；
当1lna0，即 a  e 时， f
1
 x  在  0 , 1  l n a  单调递减，在  1  l n a ,    单调递增.
若 f x 有两个零点，则
1
f
1
 1  l n a   a e  ln a  1  l n a  l n a  0 ，解得0a1. ..........................6分
a
因为 f 0 0，
1 e
f
1
 1   a  1  0 ， f
1
 2
a

 a e
2a

2
a
 a

1 
 2
a
 1


1
2
 2
a
 1
 2 

2
a

a
2
 0 ，
所以方程 a e x  1  x  0 有两个根，设为 x
1
, x
3
2
，且0x 1x  ，
1 3 a
 g  x  在  0 , x
1
 ，1,x 上单调递减，在
3
 x
1
,1  ，  x
3
,    上单调递增，
故当 0  a  1 时， g  x  有三个极值点 x
1
，x ，x ，其中x 1. ........................................................8分
2 3 2
由aex 1 1  x ，得
1
g  x
1
  l n x
1
 x
1

a e
x
x1
1
 1
 1  l n x
1
 x
1
，同理 g  x
3
  ln x
3
 x
3
，
又因为gx  g1ln11a1a2，
2
所以
g  x
1
  g  x
2
  g  x
3
  a  2  l n  x
1
x
3
   x
1
 x
3

 a  2   x
1
 x
3
  l n  a e x1  1  a e x3  1 
a2x x lna2 x 1x 1
1 3 1 3
a42lna， .................................................................................................10分
{#{QQABKQKEogAoQABAABhCEwVyCgKQkAGACCoOxBAEIAAAARFABCA=}#}令maa42lna，
0  a  1 ，
则 m   a   1 
2
a
 0 ，所以 m  a  在（0，1）上单调递增，
a  0 时， m  a     ， m  1    3 ，
所以 m  a    3 ，
所以 g  x
1
  g  x
2
  g  x
3
 的取值范围是    ,  3  ．...................................................................................12分
{#{QQABKQKEogAoQABAABhCEwVyCgKQkAGACCoOxBAEIAAAARFABCA=}#}