2023年11月诊断性测试数学答案(1)_2023年11月_0211月合集_2024届THUSSAT中学生标准学术能力诊断性测试高三上学期11月月考_THUSSAT中学生标准学术能力诊断性测试2024届高三上学期11月月考数学

中学生标准学术能力诊断性测试 2023年 11月测试
数学参考答案
一、单项选择题：本题共 8小题，每小题 5分，共 40 分．在每小题给出的四个选项中，只有
一项是符合题目要求的．
1 2 3 4 5 6 7 8
C A B B A B D D
二、多项选择题：本题共 4小题，每小题 5分，共 20 分．在每小题给出的四个选项中，有多
项符合题目要求．全部选对的得5分，部分选对但不全的得2分，有错选的得0分．
9 10 11 12
BD AC AB ACD
三、填空题：本题共4小题，每小题5分，共20分．
7
14．
13．1
2
10+ 2
15． 16．35
4
四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．
17．（10分）
2csinB sinC 2sinCsinB sinC
（1） = ，所以由正弦定理得 = ，
b cosB sinB cosB
1 
cosB = ，得B = ············································································ 3分
2 3
3
+ 3
tan A+tanB
tanC =−tan(A+B)=− =− 4 =−5 3 ················· 5分
1−tan AtanB 3
1−  3
4
（2） ABC内切圆的面积为，所以内切圆半径r=1，
由圆的切线性质得c+a−b=2 3,b=c+a−2 3=3+ 3 ····························· 7分
由余弦定理得b2 =c2+a2−ac，
 ( 3+ 3 )2 =c2 +a2 −ac=(a+c)2 −3ac，将a+c=3+3 3代入，
第1页 共8页
{#{QQABLYQUggCgQBBAAQhCAwEQCgAQkBACAAoGxAAIMAIBgRFABAA=}#}1 
ac=8+4 3,S = acsin =2 3+3 ·············································· 10分
ABC 2 3
1
（或a+b+c=6+4 3,S = r(a+b+c)=2 3+3 ······················ 10分）
ABC 2
18．（12分）
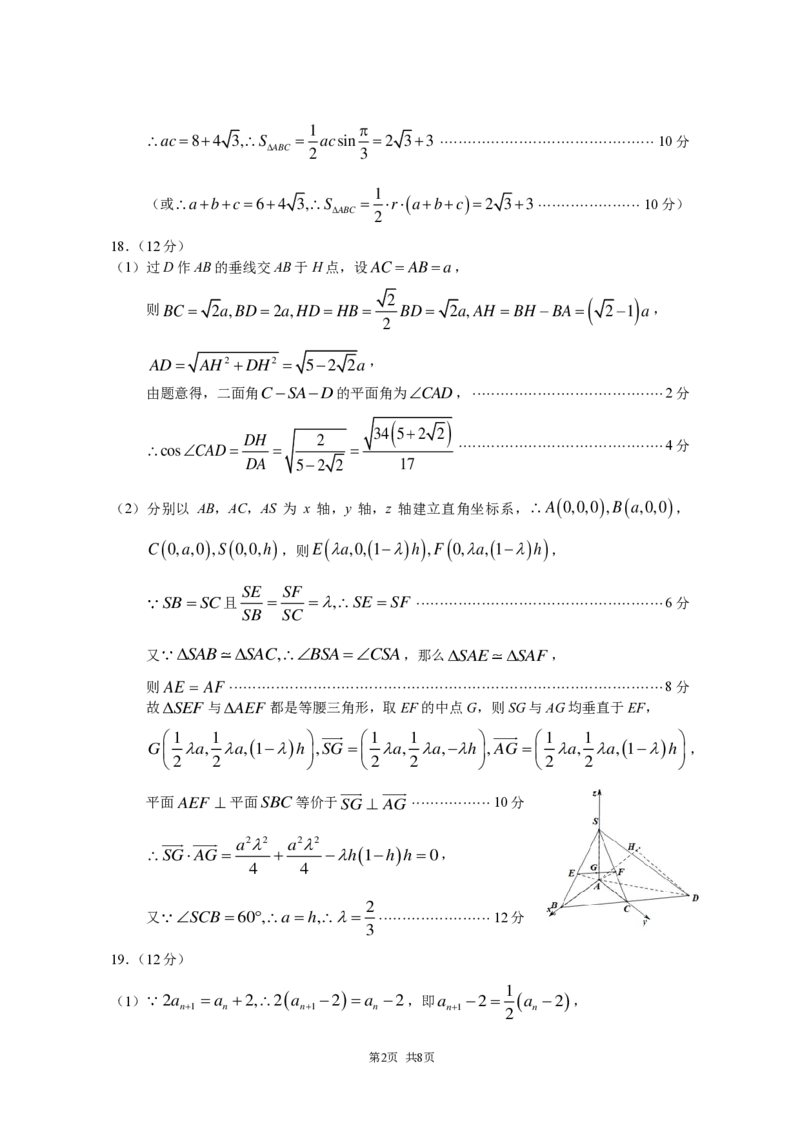
（1）过D作AB的垂线交AB于H点，设AC= AB=a，
2 ( )
则BC = 2a,BD=2a,HD= HB = BD = 2a,AH = BH −BA= 2−1 a，
2
AD= AH2 +DH2 = 5−2 2a，
由题意得，二面角C−SA−D的平面角为CAD， ········································· 2分
( )
34 5+2 2
DH 2
cosCAD= = = ············································ 4分
DA 5−2 2 17
（2）分别以 AB，AC，AS 为 x 轴，y 轴，z
轴建立直角坐标系，A(0,0,0),B(a,0,0)
，
C(0,a,0),S(0,0,h) ，则E ( a,0,(1−)h ) ,F ( 0,a,(1−)h ) ，
SE SF
SB=SC且 = =,SE = SF ····················································· 6分
SB SC
又 SAB SAC,BSA=CSA，那么SAE SAF ，
则AE = AF ····························································································· 8分
故SEF 与AEF 都是等腰三角形，取EF的中点G，则SG与AG均垂直于EF，
1 1  1 1  1 1 
G  a, a,(1−)h  ,SG =  a, a,−h  ,AG =  a, a,(1−)h  ，
2 2  2 2  2 2 
平面AEF ⊥平面SBC等价于SG ⊥ AG ················· 10分
a22 a22
SGAG = + −h(1−h)h=0，
4 4
2
又 SCB =60,a =h,= ························ 12分
3
19．（12分）
1
（1） 2a =a +2,2(a −2)=a −2，即a −2= (a −2) ，
n+1 n n+1 n n+1 2 n
第2页 共8页
{#{QQABLYQUggCgQBBAAQhCAwEQCgAQkBACAAoGxAAIMAIBgRFABAA=}#}1
a −2
是公比为 的等比数列 ······························································· 2分
n
2
n−1 n−1
1 1
a −2=3 ,a =2+3 ····················································· 4分
   
n 2 n 2
 1 1 2 1 n−1  1 n
（2） S =a +a + +a =2n+31+ +   + +    =2n+61−   
n 1 2 n  2 2 2   2 
············································································································· 6分
n n
1 1 1
S −2n−6=−6 , S −2n−6 =6  ，
   
n 2 n 2 2023
即2n−1 6069,n取最小值14 ·································································· 8分
2
n−1
C
2(n+1)
（3） C =n   , n+1 = 1，得n2，
n 3 C 3n
n
4
即C C ，有C C C ，又C =,C =C = ，
n+1 n 3 4 5 1 2 3 3
故 C  中最大项为C ,C ······································································· 10分
n 2 3
7 4 7
又 b  中最小值为2,(b ) −(C )  ，即2 −  ，
m m min n max 3 3 3
7
(3−7)(+1)0，又0,
················································· 12分
3
20．（12分）
（1）由题意可知：X的所有可能取值为2.3，0.8，0.5，
1 3 4
P(X =2.3)=   =0.3 ······································································ 1分
2 4 5
X =0.8包含的可能为“高低高”“低高高”“低低高”，
1 1 4 1 3 4 1 1 4
P(X =0.8)=   +   +   =0.5 ·········································· 2分
2 4 5 2 4 5 2 4 5
P(X =0.5)=1−0.3−0.5=0.2
··································································· 3分
X的分布列为：
X 2.3 0.8 0.5
P 0.3 0.5 0.2
第3页 共8页
{#{QQABLYQUggCgQBBAAQhCAwEQCgAQkBACAAoGxAAIMAIBgRFABAA=}#}·············································································································· 4分
数学期望E(X)=1.19
················································································ 5分
（2）设升级后一件产品的利润为Y，
Y的所有可能取值为2.3−a,0.8−a,0.5−a ····················································· 6分
1  3 4 6b+3
P(Y =2.3−a)=  +b    = ························································· 7分
2  4 5 10
1  3 4 1  1 4 1  1 4 5−6b
P(Y =0.8−a)=  −b    +  +b    +  −b    = ············· 8分
2  4 5 2  4 5 2  4 5 10
6b+3 5−6b 1
P(Y =0.5−a)=1− − = ························································ 9分
10 10 5
6b+3 5−6b 1
E(Y)=(2.3−a) +(0.8−a) +(0.5−a) =1.19+(0.9b−a)
10 10 5
············································································································ 11分
E(Y) E(X)0.9b−a0，
1 10a 1
即： b
( a0,0.4)
（备注： 不写出不扣分） ······························· 12分
2 9 2
21．（12分）
（1） AB + AF + BF =4 2，即 AF + BF + AF + BF =4 2，
1 1 2 2 1 1
又 AF + AF = BF + BF =2a,4a=4 2,a= 2 ······························· 2分
1 2 1 2
c 2
又 e= = ,c=1,b=1，
a 2
x2
故椭圆E的方程是 + y2 =1 ······································································ 4分
2
（2）依题意知直线BC的斜率存在，设直线BC:y=kx+m，
x2 x2
代入 + y2 =1，得 +(kx+m)2 =1，
2 2
1 
即 +k2  x2 +2kmx+m2 −1=0 ①，
2 
第4页 共8页
{#{QQABLYQUggCgQBBAAQhCAwEQCgAQkBACAAoGxAAIMAIBgRFABAA=}#}=(2km)2 −4 

1 +k2 

( m2 −1 ) =−2m2 +2+4k2 0，
2 
即2k2 −m2 +10 ②，
设B(x ,y ),C(x ,y ) ，则A(x ,−y ) ，
1 1 2 2 2 2
−2km m2 −1
x +x = x x =
1 2 1 ③， 1 2 1 ④ ····················································· 6分
+k2 +k2
2 2
A,F ,B三点共线，F (1,0) ，直线AB不与坐标轴垂直，
2 2
y −y
 1 = 2 ,(x −1)(kx +m)=−(x −1)(kx +m) ，
x −1 x −1 2 1 1 2
1 2
2kx x +m(x +x )−k(x +x )−2m=0，
1 2 1 2 1 2
2k ( m2 −1 ) 2km2 2k2m
 − + −2m=0
1 1 1 ，
+k2 +k2 +k2
2 2 2
2km2−2k−2km2+2k2m−m−2k2m=0，
m=−2k,直线BC: y =k(x−2) ，
1
由②得：2k2 −4k2 +10,k2  ，
2
3 k
BC = 1+k2 x −x ，点F (−1,0) 到直线BC:kx−y−2k =0的距离d = ，
1 2 1 1+k2
1 3
S = BC d = k x −x ································································· 8分
F 1 BC 2 2 1 2
2
 
 4k2  4 ( 4k2 −1 )
x −x = (x +x )2 −4x x =   −
1 2 1 2 1 2 1 1
 +k2  +k2
 2  2
第5页 共8页
{#{QQABLYQUggCgQBBAAQhCAwEQCgAQkBACAAoGxAAIMAIBgRFABAA=}#}16k4 −4 ( 4k2 −1 )1 +k2 
 
2  2−4k2
= = ，
2 2
1  1 
+k2 +k2
   
2  2 
k2( 2−4k2)
S =3 (k 0) ，
F 1 BC ( 1+2k2)2
t−1
设2k2+1=t 1，则k2 = ，
2
(t−1)(2−t) −t2 +3t−2 1 2 1
S =3 =3 =3 −2 +3 −1
 
F 1 BC t2 t2 t t
2
1 3 1
=3 −2 − + ··································································· 10分
 
t 4 8
1 3 4 4 1
所以当 = 时，即t = ,2k2 +1= ,k2 = （符合题意），
t 4 3 3 6
3 2 6 3 2
S 的最大值为 ，所以当k = 时，FBC的面积取最大值为
FBC 1
1 4 6 4
············································································································ 12分
22．（12分）
（1）定义域为
(−,−1) (1,+)
，
由题意知 ( x2 −x ) ln ( x −1 ) =ax，则 (x−1)ln ( x −1 ) =a有三个不同的实数根，
当x
1时，令g(x)=(x−1)ln(x−1)
，
g(x)=ln(x−1)+1,g(x) 在x(1,+)
上单调递增，
 1
又g

1+

=0，
 e
 1  1 
g(x) 在x  1,1+ 上单调递减，在x  1+ ,+ 上单调递增，
 e  e 
 1 1
g(x) g  1+  =− ·············································································· 2分
 e e
第6页 共8页
{#{QQABLYQUggCgQBBAAQhCAwEQCgAQkBACAAoGxAAIMAIBgRFABAA=}#}当x−1时，令h(x)=(x−1)ln(−x−1)
，
x−1 1 2 x+3
h(x)=ln(−x−1)+ ,h(x)= + =
，
x+1 x+1 (x+1)2 (x+1)2
又h(−3)=0，h(x)
在
(−,−3)
上单调递减，在
(−3,−1)
上单调递增，
h(x)h(−3)=2+ln20，
h(x)
在
(−,−1)
上单调递增 ····································································· 5分
又h(−2)=0，
当x→−1−时，h(x)→+，当x→−时，h(x)→−，
当x→1+时，g(x)→0− ，当x→+时，g(x)→+，
1
− a0 ··························································································· 6分
e
a
（2）由已知可知 (x−1)ln ( x −1 ) = 有3个零点x,x ,x ，
x 1 2 3
不妨设x x x ，
1 2 3
1
−
a 1
显然−2 x −1，由（1）中函数g(x) 性质且  e − ，
1 1 1 e
1+ 1+
e e
1
1 x 1+  x 2，
2 e 3
2 2
只需证x +x 2+ ，即x 2+ −x ···················································· 8分
2 3 e 3 e 2
  1   2   2 
又 g  2  1+  −x  −g(x )=  1+ −x  ln  1+ −x  −(x −1)ln(x −1)0，
  e 2  2  e 2   e 2  2 2
上面不等式证明如下：
 2   2   1
令(x)=  1+ −x  ln  1+ −x  −(x−1)ln(x−1),x  1,1+ ，
 e   e   e
第7页 共8页
{#{QQABLYQUggCgQBBAAQhCAwEQCgAQkBACAAoGxAAIMAIBgRFABAA=}#} 2   1
(x)=−ln

1+ −x

−ln(x−1)−2,x

1,1+

 e   e
 2  
=ln

1+ −x

(x−1)

−20，
 e  
 1
(x) 在x  1,1+ 上单调递增，
 e
 1
(x)  1+  =0 ··········································································· 10分
 e
1 2 1
又−x −1− ,2+ −x 1+ ，
2 e e 2 e
  1 
g  2  1+  −x   g(x ) ，又显然有g(x ) g(x ) ，
  e 2  2 2 3
 1
2  1+  −x  x ，
 e 2 3
2
x +x 2+ ，
2 3 e
2
x +x +x  ·················································································· 12分
1 2 3 e
第8页 共8页
{#{QQABLYQUggCgQBBAAQhCAwEQCgAQkBACAAoGxAAIMAIBgRFABAA=}#}