2025届新高三9月摸底大联考数学试卷+答案_2024-2025高三（6-6月题库）_2024年09月试卷_09232025届新高三9月摸底大联考（新课标卷）

{#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}{#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}{#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}{#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}2025 届新高三学情摸底考（新课标卷） 数学·全解全析及评分标准 阅卷注意事项： 1.阅卷前请各学科教研组长，组织本学科改卷老师开会，强调改卷纪律，统一标准。 2.请老师改卷前务必先做一遍试题，了解自己所改试题的答案、评分细则、答题角度后，再开始改卷。 3.请老师认真批阅，不可出现漏改、错改现象，如果不小心漏改或错改了，可以点击回评按钮重评。 4.成绩发布后，如果有学校反馈错评乱评，平台定位阅卷老师，进行通报批评。 5.解答题要在学生的答案中找寻有用的文字说明、证明过程或演算步骤，合理即可给分。 6.解答题不要只看结果，结果正确，但中间的文字说明、证明过程或演算步骤无法建立有效衔接的，不 能给满分；同样，结果错误，但正确写出相应的文字说明、证明过程或演算步骤应给分，因第(1)问中 结果算错，使后面最终结果出错(过程列式正确)，不宜重复扣分。 7.阅卷平台出现的相关问题，如果刷新页面重新登录未能解决，请将问题反馈给学校负责技术的老师(或 考试负责人），由其统一在技术QQ群里反馈问题并协助解决。 1 2 3 4 5 6 7 8 9 10 11 C A B D D B C A ACD AC BCD 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要 求的。 a24, 1．C 【解析】因为M {1,3,a2},N {1,a2}，M  N {1,4}，所以 解得a2.故选C. a2 4, 3a3, 2．A 【解析】设z abi,a,bR，则zabi，所以abi2(abi)3i，即3abi3i，所以 b1, a1, 3i 3i (3i)(1i) 24i 解得 所以z1i，所以    12i．故选A． b1, z 1i (1i)(1i) 2 3．B 【解析】由题意，知 a2b(32m,2) ， ab(3m,7) ．由向量 a2b 与 ab 共线，得 9 7(32m)2(3m)0，即12m27，解得m ．故选B． 4 4．D 【解析】因为 f(x)(xa)cosx为奇函数，所以 f(0)0，即a0，所以 f(x)xcosx．求导，得 f(x)cosxxsinx, 所以 f(π)1.又 f(π)π ，所以曲线 y f(x) 在点(π, f(π))处的切线方程为 y(xπ)，即x y0．故选D． π 2 π 5．D 【解析】由 2sinsin( )，得 2sin (sincos)，所以sincos，所以sin( )0， 4 2 4 数学 全解全析及评分标准 第1页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#} 1 所以 k,kZ，所以sin22cos2cos2 ．故选D． 4 2 6．B 【解析】可将x2  y2 2x0转化为(x1)2  y2 1，所以圆心为C(1,0)，设直线l:ymx2m(m0)， P为直线l上一动点.由题意，得|PC|的最小值为 2，即当PC与直线l垂直时，|PC|取得最小值 2， |3m| 14 则  2 .因为m0，解得m ．故选B． m2 1 7 7．C 【解析】取棱AC的中点M，连接BM ，DM ．因为△ABC是边长为2的等边三角形，所以BM  AC 且BM  3．又因为△ACD 为等腰直角三角形且直线BD为该筝形的对称轴，所以ADCD 2 ， DM  AC 且DM  AM CM 1．又因为BD2，所以△BMD为直角三角形，且BM DM ．过△ABC 的外接圆圆心O作直线l 平面ABC，过点M作直线l 平面ACD，直线l 与直线l 相交于点O，则 1 2 1 2 2 3 点O为四面体ABCD外接球的球心，计算，得四面体ABCD外接球的半径R ，所以四面体ABCD 3 16π 外接球的表面积S 4πR2  ．故选C． 3 8．A 【解析】设M(x,y)(x0,y0)，则N(x,y)， y y  tanNAOtanMAO xa xa 2xy 2xy tantan(NAOMAO)     1tanNAOtanMAO y y a2 x2  y2 a2 1  (1 )y2 xa xa b2 2x y 2b2 b2 b2 .又tan ，所以tantan 3，即 3，所以e2 1 4，即e2， a2 x b2 a2 a2 a2 (1 )y b2 所以双曲线C的离心率为2.故选A． 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求，全部 选对的得6分，部分选对的得部分分，有选错的得0分。 9．ACD 【解析】对于A，由题意，知事件A表示摸出的两个球的编号为1,2或1,3，事件A 表示摸出的两 1 2 个球的编号为3,4，所以事件A与事件A 是互斥事件，故A正确； 1 2 对于B，事件A 表示摸出的两个球的编号为1,3或2,3或3,4，因为A A ，所以事件A与事件A 不 3 1 3 1 3 是对立事件，故B错误； 1 1 1 对于C，因为P(A) ，P(A ) ，P(AA ) ，所以P(AA)P(A)P(A)，所以事件A与事件A 是 1 3 3 2 1 3 6 1 3 1 3 1 3 相互独立事件，故C正确； 对于D，因为事件A A 表示摸出的两个球的编号为3,4，事件A A 表示摸出的两个球的编号为1,3， 2  3 1 3 数学 全解全析及评分标准 第2页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}所以事件A A 与事件A A 是互斥事件，故D正确． 2  3 1 3 故选ACD．   10．AC 【解析】由题意，知点M( 3cos x, 3sin x). 2 2 π 1 π 3 π π 对于A，(x)( 3cos x )2 ( 3sin x )2 42 3cos( x )，故A正确； 2 2 2 2 2 3 20 π 20 π 对于B，当x 时，(x)42 3cos(   )42 3cos3π42 3，为最大值，故B错误； 3 2 3 3    5 5 对于C，令 x  kkZ，解得x 2k,kZ，所以点( ,4)是曲线y(x)的一个对称中 2 3 2 3 3 心，故C正确； π π 2 8 对于D，令2kπ x 2kππ，kZ，解得4k  x4k ，kZ.又x[0,4)，所以k 0， 2 3 3 3 2 8 2 8  x ，所以(x)的单调递增区间为[ , ]，故D错误. 3 3 3 3 故选AC． 11．BCD 【解析】对于A，令x y0，得 f(0)0，令yx，得 f(x) f(x)0，所以 f(x)为奇函数， 故A错误； 对于B，令x y1，得 f(2)2f(1)2，令x1,y2，得 f(3) f(1) f(2)6，又 f(3)12，所以 4 4 3f(1)812，所以 f(1) ， f(1)f(1) ，故B正确； 3 3 (x y)3 x3 y3 对于C，由 f(x y) f(x) f(y)xy2 x2y，得 f(x y)  f(x)  f(y) ， 3 3 3 x3 记g(x) f(x) ，则g(x y) g(x)g(y)，且g(x)也为奇函数. 3 又当x0时，3g(x)3f(x)x3 0，即g(x)0.下面证明g(x)在(0,)上单调递增， 设x x 0，则g(x )g(x)g(x )g(x)g(x x )0， 2 1 2 1 2 1 2 1 即当x x 0时，g(x )g(x)，所以g(x)在(0,)上单调递增. 2 1 2 1 又g(x)为奇函数，当x0时，g(x)0，所以g(x)在R上单调递增， x3 所以 f(x)g(x) 在R上单调递增，故C正确； 3 对于D，令y1，得 f(x1) f(x) f(1)x2 x，所以 f(x1) f(x)2x1. 又 f(x)为奇函数，所以 f(x)为偶函数. π π π π  因为 f(sin( 1)) f(1), f(sin( 2)) f(0), f(sin( 3)) f(1), f(sin( 4)) f(0)，及 f(sin x) 2 2 2 2 2 的周期为4， 2024 π 所以 f(sin i)506[f(1) f(0) f(1) f(0)]1012[f(1) f(0)]. 2 i1 数学 全解全析及评分标准 第3页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}由 f(3) f(2)5 f(1)8 f(0)910, 解得 f(1)2, f(0)1， 2024 π 所以 f(sin i)1012[f(1) f(0)]3036，故D正确． 2 i1 故选BCD． 三、填空题：本题共3小题，每小题5分，共15分。 12．23【解析】因为(x3)8的展开式中xk的系数为C8 8 k(3)8k ，k 0,1,  ,8，所以所求的x9的系数为 C1(3)1C0(3)0 24123．故填23. 8 8 1 1 3 3 π 13． 3或 7 【解析】由S  absinC  21sinC  ，得sinC  .因为0C ,所以C  △ABC 2 2 2 2 3 2 π  或C  .当C  时，由余弦定理，得c2 a2 b2 2abcosC 22 12 221cos ，解得c 3； 3 3 3 2 2 当C  时，由余弦定理，得c2 a2 b2 2abcosC 22 12 221cos ，解得c 7．故填 3 3 3 或 7 ． yx(x0) 3 2  14．( ,) 【解析】由题意，知射线OP:y x(x0)，|OR|b，|OT |a，联立x2 y2 ，得 4   1 a2 b2 a2b2 a2b2 |OR||OT| a2 b2 x y ，|OS| 2 ，所以  .又圆C 与圆C 围成的图形的面积大 a2 b2 a2 b2 |OS|2 2ab 1 2 a2 1 a |OR||OT | a2 b2 b2 于圆C 的面积，所以πa2 πb2 πb2，即a2 2b2，所以  2 ，所以    1 b |OS|2 2ab a 2 b 1 a 1 a 1 |OR||OT| 3 2 3 2 (  )，令t  ，又yt 在( 2,)上单调递增，所以  .故填( ,)． 2 b a b t |OS|2 4 4 b 说明： 1．第12题不用数字作答不给分； 2．第13题只写 3或只写 7 均不给分； |OR||OT| 3 2 3．第14题写  也给5分. |OS|2 4 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15．（13分） 【解析】（1）设事件M “至少选到2箱A级苹果”. 数学 全解全析及评分标准 第4页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}3 由题意，知选到1箱A级苹果的概率为 ，（1分） 5 3 2 所以选到1箱非A级苹果的概率为1  ，（2分） 5 5 3 2 3 81 所以P(M)C2( )2 C3( )3  ， 3 5 5 3 5 125 81 即至少选到2箱A级苹果的概率为 .（4分） 125 （2）由题意，知选出的10箱苹果中，A级苹果有6箱，B,C级苹果共有4箱．（5分） X 的所有可能取值为0,1,2,3，（6分） C3 1 C2C1 3 C1C2 1 C3 1 且P(X 0) 4  ,P(X 1) 4 6  ,P(X 2) 4 6  ,P(X 3) 6  ，（10分） C3 30 C3 10 C3 2 C3 6 10 10 10 10 所以X 的分布列为 X 0 1 2 3 1 3 1 1 P 30 10 2 6 （11分） 1 3 1 1 E(X)0 1 2 3 （12分） 30 10 2 6 9  ．（13分） 5 说明： 第一问： 1.1分段设至少选到2箱A级苹果为事件M ,正确求出选到1箱A级苹果的概率，不设出事件M 不扣分； 2.2分段求出选到1箱非A级苹果的概率； 3.4分段求出至少选到2箱A级苹果的概率，分开写选到2箱A级苹果和3箱A级苹果的概率，有一 个正确给1分，答案写成0.648也给分. 第二问： 1.5分段写出用分层随机抽样的方法，得到A级苹果有6箱，B,C级苹果共有4箱； 2.6分段写出X的所有可能取值，有错不给分； 3.10分段写出X取每一个值的概率，对一个给1分，所有结果都正确但是结果不是最简的扣1分； 4.11分段写出X的分布列，不化简不重复扣分； 5.12分段列出E(X)的式子； 6.13分段算出E(X)的值. 数学 全解全析及评分标准 第5页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}16．（15分） 1 1 【解析】（1）设等比数列{a }的公比为q(q0)，由a  ，得aq2  .（1分） n 3 4 1 4 1 1 由aa  ，得a2q ，（2分） 1 2 2 1 2 1 解得a 1,q ，（4分） 1 2 1 1 所以a  ，即{a }的通项公式为a  ．（5分） n 2n1 n n 2n1 （2）由（1），知b n1，（6分） n 由S a b a b  a b ab ，即S ab a b  a b a b ， n n 1 n1 2  2 n1 1 n n 1 n 2 n1  n1 2 n 1 n1 n n1 3 2 得S       ，（8分） n 20 2 22  2n2 2n1 1 n1 n n1 3 2 S       ，（10分） 2 n 2 22 23  2n1 2n 1 1 1 1 1 2 两式相减，得 S (n1)(     ) （12分） 2 n 2 22 23  2n1 2n 1 1 (1 ) 2 2n1 2 (n1)  （13分） 1 2n 1 2 1 2 (n1)1  n，（14分） 2n1 2n 所以S 2n．（15分） n 说明： 第一问： 1 1.1分段将a  用a，q表示； 3 4 1 1 2.2分段将aa  用a，q表示； 1 2 2 1 3.4分段计算出a，q,对1个给1分； 1 4.5分段写出{a }的通项公式. n 第二问： 1.6分段算出b n1； n 2.8分段将S 倒序后写出； n 数学 全解全析及评分标准 第6页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}1 3.10分段将等式两边同时乘以 ； 2 4.12分段两式相减； 5.13分段利用等比数列求和公式求和； 6.14分段化简得出结果； 7.15分段得出S . n 2 3 4 n1 8.8分段S 不倒序，直接利用S      求和，按以下步骤给分： n n 2n1 2n2 2n3  20 2 3 4 n1 S      ，（8分） n 2n1 2n2 2n3  20 2 3 4 n 2S      2(n+1)，（10分） n 2n2 2n3 2n4  20 两式相减，得 2 1 1 1 S  (    )2(n+1)（12分） n 2n1 2n2 2n3  20 1 1[1( )n1] 2 2   2(n1)（13分） 2n1 1 1 2 2 1  22( )n12(n1)2n，（14分） 2n1 2 所以S 2n．（15分） n 17．（15分） 【解析】（1）因为PD平面ABCD，BC平面ABCD，所以PDBC .（1分） 又底面ABCD为矩形，所以BC CD.（2分） 又PD CD D，PD，CD平面PCD，所以BC 平面PCD.（3分）  又BC平面PBC ，所以平面PCD平面PBC ．（4分） （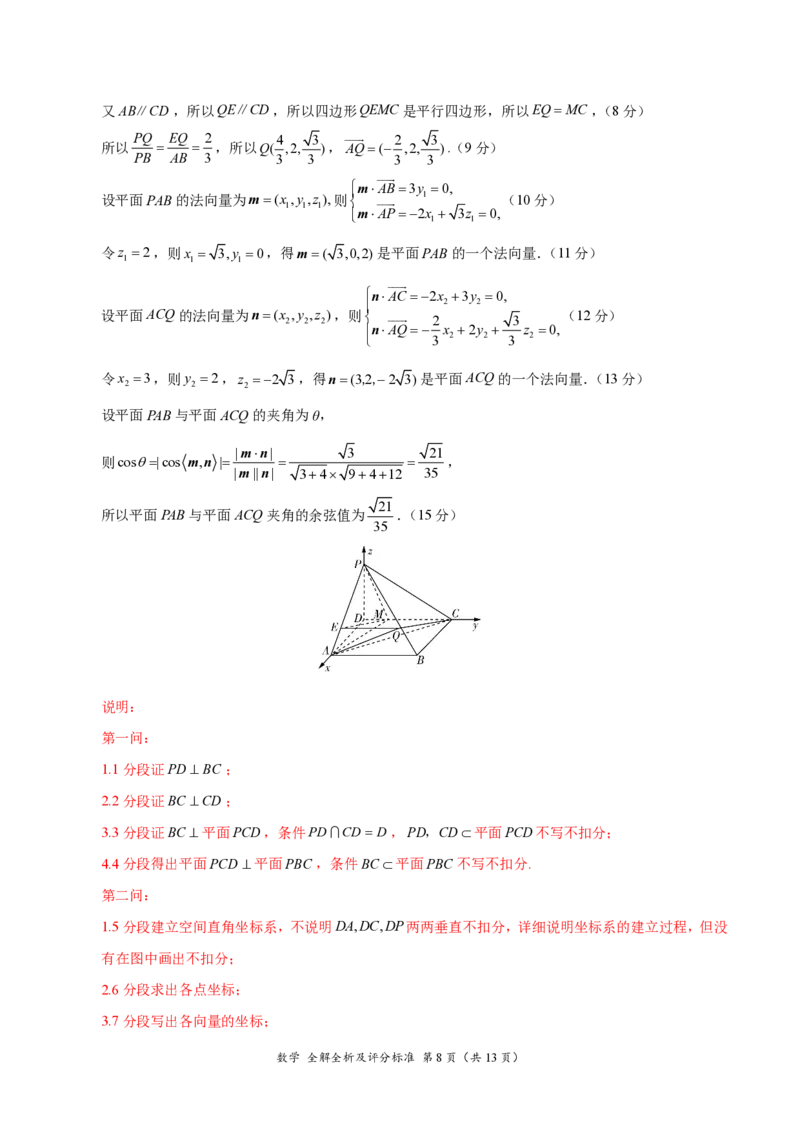2）因为DA,DC,DP两两垂直，所以以D为坐标原点，DA，DC，DP所在的直线分别为x轴、y轴、 z轴建立如图所示的空间直角坐标系，（5分） 则A(2,0,0)，B(2,3,0)，C(0,3,0), 由题意，知在Rt△PDM 中，PDM 90,PM 2,DM 1，所以PD 3，所以P(0,0, 3)，（6分）    AC (2,3,0),AB(0,3,0),AP(2,0, 3).（7分） 过点Q作QE∥AB交PA于点E，连接EM ， 因为CQ∥平面PAM ，所以CQ∥EM . 数学 全解全析及评分标准 第7页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}又AB∥CD，所以QE∥CD，所以四边形QEMC是平行四边形，所以EQMC ，（8分） PQ EQ 2 4 3  2 3 所以   ，所以Q( ,2, )，AQ( ,2, ).（9分） PB AB 3 3 3 3 3   mAB3y 0, 设平面PAB的法向量为m(x 1 ,y 1 ,z 1 ),则  1 （10分） mAP2x  3z 0, 1 1 令z 2，则x  3,y 0，得m( 3,0,2)是平面PAB的一个法向量．（11分） 1 1 1  nAC 2x 3y 0,  2 2 设平面ACQ的法向量为n(x 2 ,y 2 ,z 2 )，则  2 3 （12分） nAQ x 2y  z 0,  3 2 2 3 2 令x 3，则y 2，z 2 3，得n(3,2,2 3)是平面ACQ的一个法向量．（13分） 2 2 2 设平面PAB与平面ACQ的夹角为θ， |mn| 3 21 则cos|cos m,n |   ， |m||n| 34 9412 35 21 所以平面PAB与平面ACQ夹角的余弦值为 ．（15分） 35 说明： 第一问： 1.1分段证PDBC ； 2.2分段证BC CD； 3.3分段证BC 平面PCD，条件PD CD D，PD，CD平面PCD不写不扣分；  4.4分段得出平面PCD平面PBC ，条件BC平面PBC 不写不扣分. 第二问： 1.5分段建立空间直角坐标系，不说明DA,DC,DP两两垂直不扣分，详细说明坐标系的建立过程，但没 有在图中画出不扣分； 2.6分段求出各点坐标； 3.7分段写出各向量的坐标； 数学 全解全析及评分标准 第8页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}4.8分段确定Q点位置，得出EQMC ,只要说明Q为PB上靠近B的三等分点就给分；  5.9分段得出Q点坐标和AQ； 6.10分段写出平面PAB的法向量满足的关系； 7.11分段求出平面PAB的一个法向量； 8.12分段写出平面ACQ的法向量满足的关系； 9.13分段求出平面ACQ的一个法向量； 3 10.15分段得出平面PAB与平面ACQ夹角的余弦值，结果写成 不扣分. 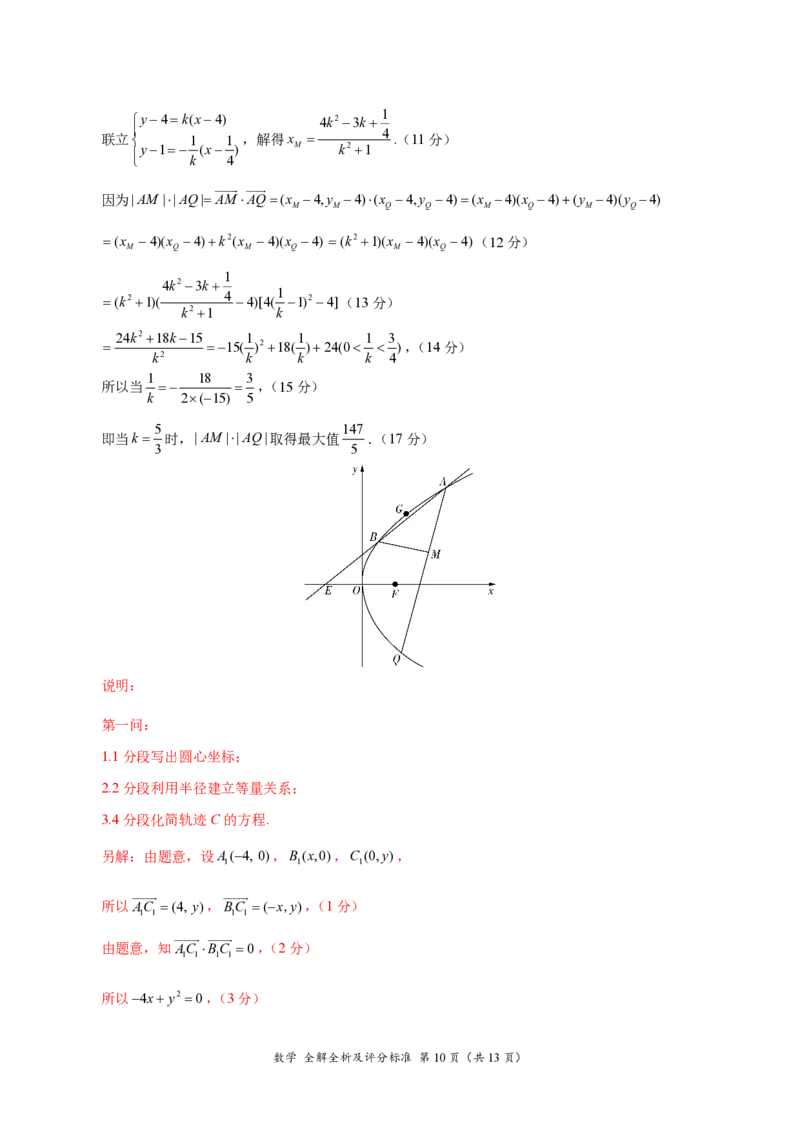5 7 18．（17分） x4 【解析】（1）由题意，知动圆的圆心为( ,0)，（1分） 2 x4 x4 所以( )2  y2 ( 4)2，（2分） 2 2 化简，得y2 4x，即点(x,y)的轨迹C的方程为y2 4x．（4分） （2）如图，由题意，知A(4, 4)，（5分） y2 设B( 0 ,y )(y 4)， 4 0 0 40 y 0 由A，B，E三点共线，得  0 ，（6分） 41 y2 0 1 4 1 解得y 1或y 4（舍去），所以B( ,1)，（7分） 0 0 4 1 所以点B关于x轴的对称点为B( ，1). 4 4 由题意，知直线AQ的斜率k存在，记直线AB' 的斜率为k ,且k k  ， AB' AB 3 4 设直线AQ：y4k(x4)(k  )，Q(x ,y )，M(x ,y )， 3 Q Q M M 因为点Q在抛物线C上， y4k(x4) 4 16 16 由 ，得y2  y 160，所以y y  16，（8分） y2 4x k k A Q k 4 y2 1 所以y  4，所以x  Q 4( 1)2.（9分） Q k Q 4 k 1 1 又因为BM  AQ，所以直线BM 的方程为y1 (x )．（10分） k 4 数学 全解全析及评分标准 第9页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}1 y4k(x4) 4k2 3k  4 联立 1 1 ，解得x  .（11分） y1 (x ) M k2 1   k 4   因为|AM ||AQ| AM AQ(x 4,y 4)(x 4,y 4)(x 4)(x 4)(y 4)(y 4) M M Q Q M Q M Q (x 4)(x 4)k2(x 4)(x 4) (k2 1)(x 4)(x 4)（12分） M Q M Q M Q 1 4k2 3k (k2 1)( 4 4)[4( 1 1)2 4]（13分） k2 1 k 24k2 18k15 1 1 1 3  15( )2 18( )24(0  )，（14分） k2 k k k 4 1 18 3 所以当   ，（15分） k 2(15) 5 5 147 即当k  时，|AM ||AQ|取得最大值 ．（17分） 3 5 说明： 第一问： 1.1分段写出圆心坐标； 2.2分段利用半径建立等量关系； 3.4分段化简轨迹C的方程. 另解：由题意，设A(4, 0)，B(x,0)，C (0,y)， 1 1 1   所以AC (4, y)，BC (x, y)，（1分） 1 1 1 1   由题意，知AC BC 0，（2分） 1 1 1 1 所以4x y2 0，（3分） 数学 全解全析及评分标准 第10页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}所以y2 4x，即点(x,y)的轨迹C的方程为y2 4x．（4分）   1.1分段写出AC ，BC 的坐标； 1 1 1 1   2.2分段得出AC BC 0； 1 1 1 1 3.3分段由数量积运算得出4x y2 0； 4.4分段得出轨迹C的方程. 第二问： 1.5分段求出A点的坐标； 2.6分段由三点共线得出B点坐标满足的关系； 3.7分段求出B点的坐标； 4.8分段设出直线AQ的方程，并与抛物线方程组成方程组写出根与系数的关系； 5.9分段求出Q点的坐标； 6.10分段写出直线BM的方程； 7.11分段解出M点的横坐标； 8.12分段将|AM ||AQ|用x ,x 表示； M Q 9.13分段将x ,x 代入转化为用k表示； M Q 10.14分段化简为关于k的二次函数； 11.15分段求出二次函数在对称轴处取得最大值； 12.17分段得出|AM ||AQ|的最大值； 5 13.求解过程中没有估计出k的取值范围，最后不检验k  是否取到扣1分. 3   或者第二问也可以将求|AM ||AQ|的最大值转化成求ABAQ的最大值. 19．（17分） 【解析】（1）由 f(x)x(x1)(x2)(x4)，得 f(0) f(1) f(2) f(4)0，（1分） 由 f(0) f(1)，根据罗尔定理，知存在x (0,1)，使得 f(x)0，（2分） 1 1 由 f(1) f(2)，根据罗尔定理，知存在x (1,2)，使得 f(x )0，（3分） 2 2 由 f(2) f(4)，根据罗尔定理，知存在x (2,4)，使得 f(x )0， 3 3 所以方程 f(x)0至少有三个根.（4分） 数学 全解全析及评分标准 第11页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}又 f(x)为三次函数，所以方程 f(x)0至多有三个根，所以方程 f(x)0有三个根，且x (0,1)， 1 x (1,2)，x (2,4)．（5分） 2 3 f(b) f(a) （2）令F(x) f(x) x，则F(a)F(b).（6分） ba 因为 f(x)在闭区间[a,b]上连续，在开区间(a,b)内可导，所以函数F(x)在闭区间[a,b]上连续，在开区 间(a,b)内可导，且F(a)F(b)，由罗尔定理，知在开区间(a,b)内至少存在一点c，使得F(c)0. （8分） f(b) f(a) f(b) f(a) 由F(x) f(x) x，得F(x) f(x) ，（9分） ba ba f(b) f(a) 所以F(c) f(c) 0， ba f(b) f(a) 即在开区间(a,b)内至少存在一点c，使得 f(c) ，即 f(b) f(a) f(c)(ba)．（10分） ba ab （3）由0ab，得0a b， 2 ab (ab) ab (ab) ab 要证(ab)e 2 aea beb，即证 e 2 aea beb  e 2 .（11分） 2 2 令g(x)xex，由（2），得 ab ab ab g( )g(a) e 2 aea ab ab 2 2 对于区间(a, )，存在c (a, )，使得g'(c )  ，（13分） 2 1 2 1 ab ba a 2 2 ab ab ab g(b)g( ) beb  e 2 ab ab 2 2 对于区间( ,b)，存在c ( ,b)，使得g'(c )  .（15分） 2 2 2 2 ab ba b 2 2 因为g(x)(1x)ex，令h(x)(1x)ex,x0，则h'(x)(2x)ex 0，所以g'(x)在(0,)上单调递增， 又0c c ，所以g(c )g(c )，（16分） 1 2 1 2 ab ab ab ab e 2 aea beb  e 2 2 2 ab ab ab ab 即  ，即 e 2 aea beb  e 2 ， ba ba 2 2 2 2 ab 即(ab)e 2 aea beb．（17分） 说明： 第一问： 1.1分段得出 f(0) f(1) f(2) f(4)0，不写等于0也给分； 数学 全解全析及评分标准 第12页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}2.2分段由 f(0) f(1)，得x (0,1)， f(x)0； 1 1 3.3分段由 f(1) f(2)，得x (1,2)， f(x )0； 2 2 4.4分段由 f(2) f(4)，得x (2,4)， f(x )0； 3 3 5.5分段由 f(x)为三次函数得 f(x)0至多有三个根，并得出根的取值范围； 6.4分段不写 f(x)0至少有三个根不扣分，而直接说 f(x)0有三个根扣1分. 第二问： 1.6分段构造函数F(x),满足F(a)F(b)，不写F(a)F(b)不扣分； 2.8分段说明F(x)在[a,b]上满足罗尔定理，不写F(a)F(b)扣1分，不写F(x)在闭区间[a,b]上连续， 在开区间(a,b)内可导不扣分； 3.9分段求出F(x)； 4.10分段由F(c)0得出 f(b) f(a) f(c)(ba). 第三问： (ab) ab (ab) ab ab 1.11分段由分析法得出只要证 e 2 aea beb  e 2 ，不说明0a b不扣分； 2 2 2 ab 2.13分段设g(x)xex，并在(a, )上利用（2）的结论； 2 ab 3.15分段在( ,b)上利用（2）的结论； 2 4.16分段得出g(x)的单调性； 5.17分段由g(x)的单调性得出g(c)，g(c )的大小关系，并化简得出结果. 1 2 数学 全解全析及评分标准 第13页（共13页） {#{QQABYYAAggCgQIBAABgCQwkKCAOQkAAACagOhBAIMAAAgRFABAA=}#}