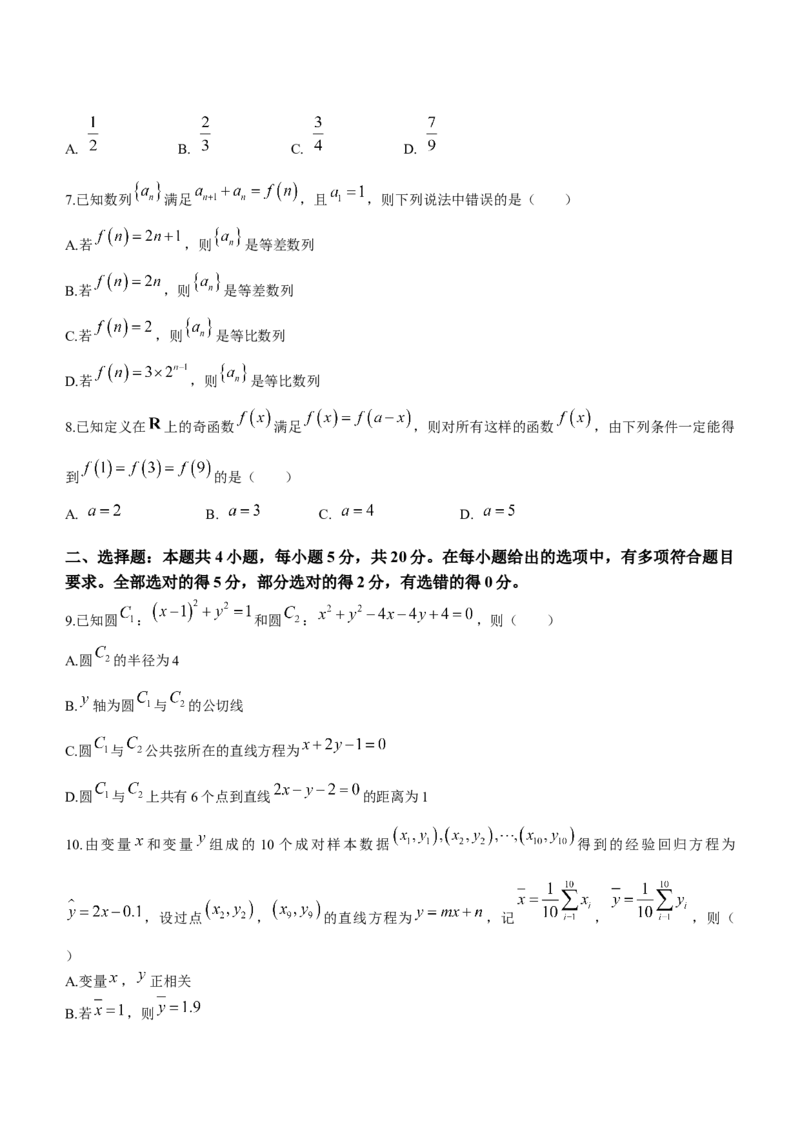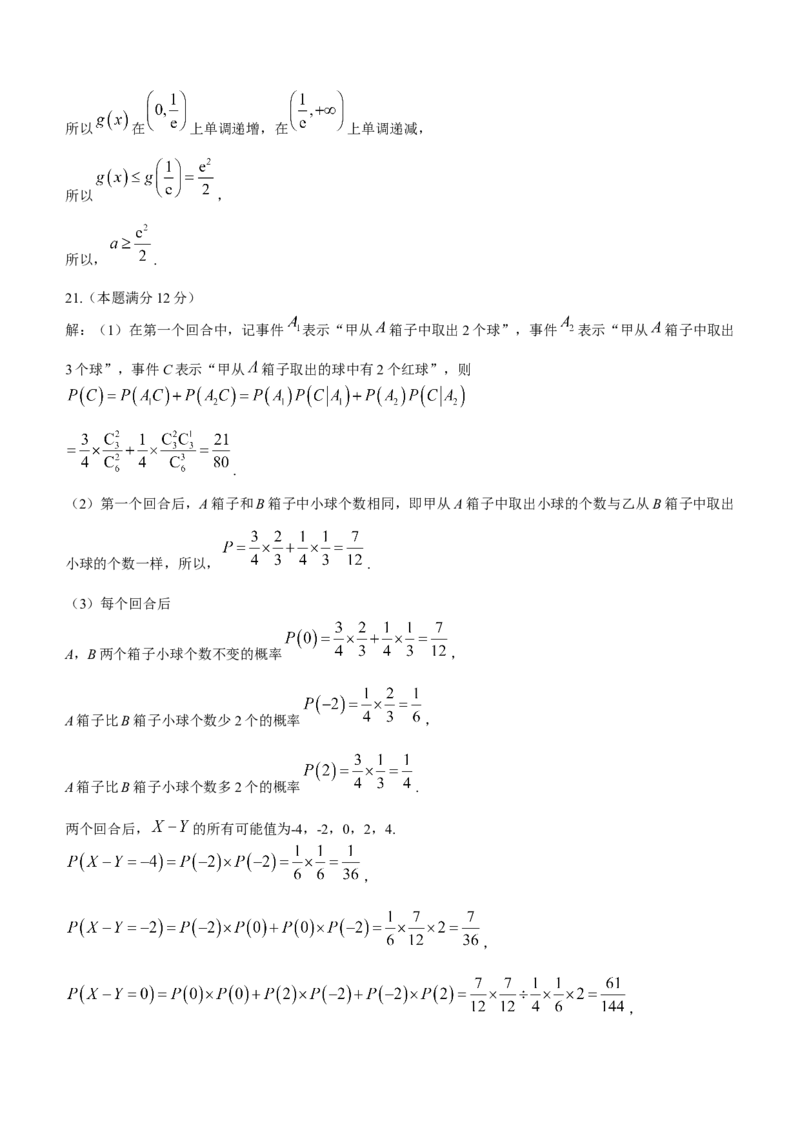文档内容
2023 年 11 月绍兴市选考科目诊断性考试
数学试题
本科试题卷分选择题和非选择题两部分,全卷共 6页,选择题部分1至3页,非选择题部分3
至6页,满分150分,考试时间120分钟。
考生注意:
1.答题前,请务必将自己的学校、班级、姓名、座位号用黑色字迹的签字笔或钢笔分别填写在
试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题
卷上的作答一律无效。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是
符合题目要求的。
1.已知集合 , ,则 ( )
A. B. C. D.
2.已知 ,则 ( )
A. B. C. D.
3.已知向量 , 满足 , , ,则 与 的夹角为( )
A. B. C. D.
4.已知某正六棱柱的所有棱长均为2,则该正六棱柱的外接球的表面积为( )
A. B. C. D.
5.“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.已知 为抛物线 上的一点,过 作圆 的两条切线,切点分别为 A,B,则
的最小值是( )A. B. C. D.
7.已知数列 满足 ,且 ,则下列说法中错误的是( )
A.若 ,则 是等差数列
B.若 ,则 是等差数列
C.若 ,则 是等比数列
D.若 ,则 是等比数列
8.已知定义在 上的奇函数 满足 ,则对所有这样的函数 ,由下列条件一定能得
到 的是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目
要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知圆 : 和圆 : ,则( )
A.圆 的半径为4
B. 轴为圆 与 的公切线
C.圆 与 公共弦所在的直线方程为
D.圆 与 上共有6个点到直线 的距离为1
10.由变量 和变量 组成的 10 个成对样本数据 得到的经验回归方程为
,设过点 , 的直线方程为 ,记 , ,则(
)
A.变量 , 正相关
B.若 ,则C.经验回归直线 至少经过 中的一个点
D.
11.已知函数 ,则( )
A. B. 恰有5个零点
C. 必有极值点 D. 在 上单调递减
12.已知椭圆 的左项点为 ,上、下顶点分别为 , ,动点 , 在椭圆上
(点P在第一象限,点Q在第四象限),O是坐标原点,若 的面积为1,则( )
A. 为定值 B.
C. 与 的面积相等 D. 与 的面积和为定值
三、填空题:本题共4小题,每小题5分,共20分。
13. 的展开式中 的系数为___________(用数字作答).
14.人类已进入大数据时代.目前,数据量已经从TB(1TB=1024GB)级别跃升到PB(1PB=1024TB),EB
(1EB=1024PB)乃至ZB(1ZB=1024EB)级别.国际数据公司(IDC)的研究结果表明,2008年全球产生的
数据量为 0.500ZB,2010 年增长到 1.125ZB.若从 2008 年起,全球产生的数据量 P 与年份 的关系为
,其中 , 均是正的常数,则2023年全球产生的数据量是2022年的___________倍.
15.过正三棱锥 的高 的中点作平行于底面 的截面 ,若三棱锥, 与三棱
台 的表面积之比为 ,则直线 与底面 所成角的正切值为___________.
16.已知等比数列 满足 且 ,则 的取值范围是___________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)记 的内角A,B,C的对边分别为a,b,c,已知 .
(1)求B的大小;
(2)若 , ,求 .
18.(12分)
已知等差数列 满足 ,且 , , 成等比数列.
(1)求 的通项公式;
(2)记 为数列 前 项的乘积,若 ,求 的最大值.
19.(12分)
如图, 为正三角形, 平面 , 平面 , , ,点F,P分
别为 , 的中点,点 在线段 上,且 .
(1)证明:直线 与直线 相交;
(2)求平面 与平面 夹角的余弦值.
20.(12分)
已知函数 .
(1)当 时,求曲线 在 处的切线方程;
(2)若 ,都有 ,求 的取值范围.
21.(12分)机器人甲、乙分别在A,B两个不透明的箱子中取球,甲先从A箱子中取2个或3个小球放入B箱子,然后乙
再从B箱子中取2个或3个小球放回A箱子,这样称为一个回合.已知甲从A箱子中取2个小球的概率为 ,
取3个小球的概率为 ,乙从B箱子中取2个小球的概率为 ,取3个小球的概率为 .现A,B两个箱子各
有除颜色外其它都相同的6个小球,其中A箱子中有3个红球,3个白球;B箱子中有2个红球,4个白球.
(1)求第一个回合甲从A箱子取出的球中有2个红球的概率;
(2)求第一个回合后A箱子和B箱子中小球个数相同的概率;
(3)两个回合后,用X表示A箱子中小球个数,用Y表示B箱子中小球个数,求 的分布列及数学期望.
22.(12分)
已知双曲线 ,过点 的直线 与该双曲线的左、右两支分别交于点A,B.
(1)当直线 的斜率为 时,求 ;
(2)是否存在定点 ,使得 ?若存在,求点 的坐标;若不存在,请说明
理由.
2023 年 11 月绍兴市选考科目诊断性考试
数学参考答案及评分标准
一、选择题:本题共8小题,每小题5分,共40分。
1.C 2.A 3.B 4.D 5.A 6.C 7.B 8.C
二、选择题:本题共4小题,每小题5分,共20分。
9.BD 10.ABD 11.BCD 12.ABC
三、填空题:本题共4小题,每小题5分,共20分。
13.-8 14.1.5 15. 16.
四、解答题:本题共6小题,共70分。
17.(本题满分10分)
解:(1)因为 ,所以 ,
即 ,所以 ,
因为 ,所以 ,所以 ,又 ,所以 .
(2)因为 ,所以 .
因为 ,
所以 .
18.(本题满分12分)
解:(1)设 的公差为 ,由 得 ;
由 , , 成等比数列,得 ,即 ,
整理得 .
由 解得 或
所以, 的通项公式为 或 .
(2)因为 ,所以 .
所以,当 时, ;当 时, .
从而 , , , , ,
又因为 , ,
所以, 的最大值为 .
19.(本题满分12分)
(1)证明:取 中点 ,连接 , , , ,则 , ,
因为 平面 , 平面 ,所以 , ,
所以 , ,则四边形 为平行四边形,所以 , .
因为点 在线段 上,且 ,所以 是 的中点,
又因为点 是 的中点,
所以 , ,
所以 , ,
即 , 共面,且 , 长度不等,
所以直线 与直线 相交.
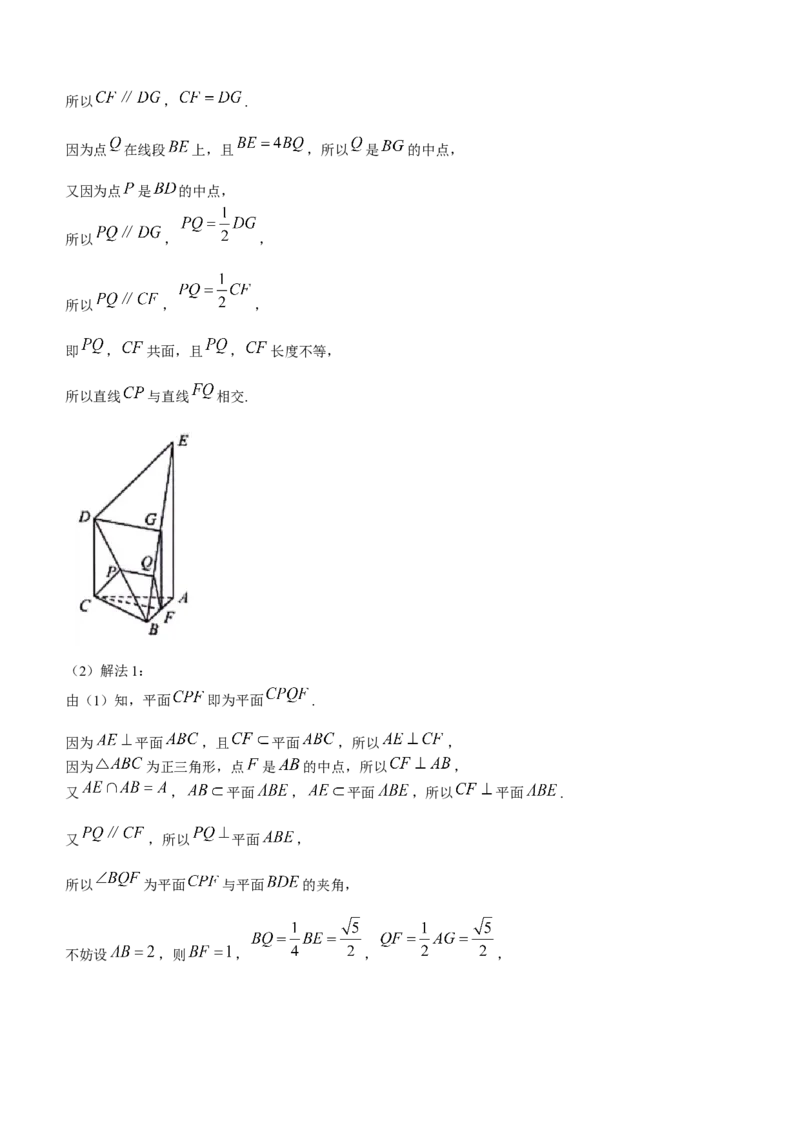
(2)解法1:
由(1)知,平面 即为平面 .
因为 平面 ,且 平面 ,所以 ,
因为 为正三角形,点 是 的中点,所以 ,
又 , 平面 , 平面 ,所以 平面 .
又 ,所以 平面 ,
所以 为平面 与平面 的夹角,
不妨设 ,则 , , ,所以 ,
即平面 与平面 夹角的余弦值为 .
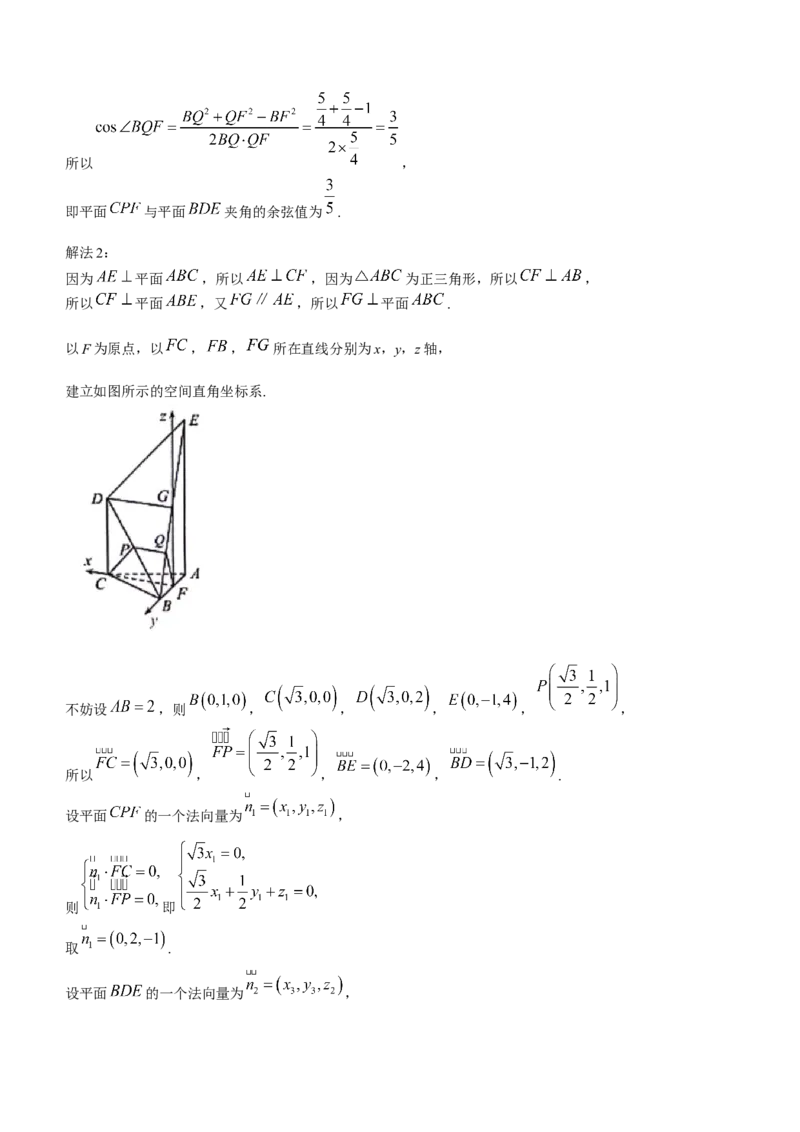
解法2:
因为 平面 ,所以 ,因为 为正三角形,所以 ,
所以 平面 ,又 ,所以 平面 .
以F为原点,以 , , 所在直线分别为x,y,z轴,
建立如图所示的空间直角坐标系.
不妨设 ,则 , , , , ,
所以 , , , .
设平面 的一个法向量为 ,
则 即
取 .
设平面 的一个法向量为 ,则 即
取 .
设平面 与平面 的夹角为 ,则 ,
所以,平面 与平面 夹角的余弦值为 .
20.(本题满分12分)
解:(1)当 时, , ,
因为 , ,
所以,曲线 在 处的切线方程是 ,即 .
(2)因为 ,都有 ,所以 ,
设 ,则 .
记 ,设 ,则 ,
所以 在 上单调递增,在 上单调递减,
所以 ,
所以 ,所以 在 上单调递减.
因为 ,所以 在 上单调递增,在 上单调递减,
所以 ,
所以, .
21.(本题满分12分)
解:(1)在第一个回合中,记事件 表示“甲从 箱子中取出2个球”,事件 表示“甲从 箱子中取出
3个球”,事件C表示“甲从 箱子取出的球中有2个红球”,则
.
(2)第一个回合后,A箱子和B箱子中小球个数相同,即甲从A箱子中取出小球的个数与乙从B箱子中取出
小球的个数一样,所以, .
(3)每个回合后
A,B两个箱子小球个数不变的概率 ,
A箱子比B箱子小球个数少2个的概率 ,
A箱子比B箱子小球个数多2个的概率 .
两个回合后, 的所有可能值为-4,-2,0,2,4.
,
,
,,
.
所以随机变量 的分布列为
-4 -2 0 2 4
所以, .
22.(本题满分12分)
解:(1)直线 的方程为 ,
设 , ,
由 得 ,所以 , ,
所以, .
(2)因为 ,所以 ,
所以 ,所以 ,
又由 得 ,所以 .
设 , ,直线 的方程为 ,其中 ,
由 得 ,所以 , .
因为 , , ,
所以 ,
,
所以 ,
整理得 ,
将 , 代入上式,整理得 ,
所以 .
经检验,存在 ,使得 .