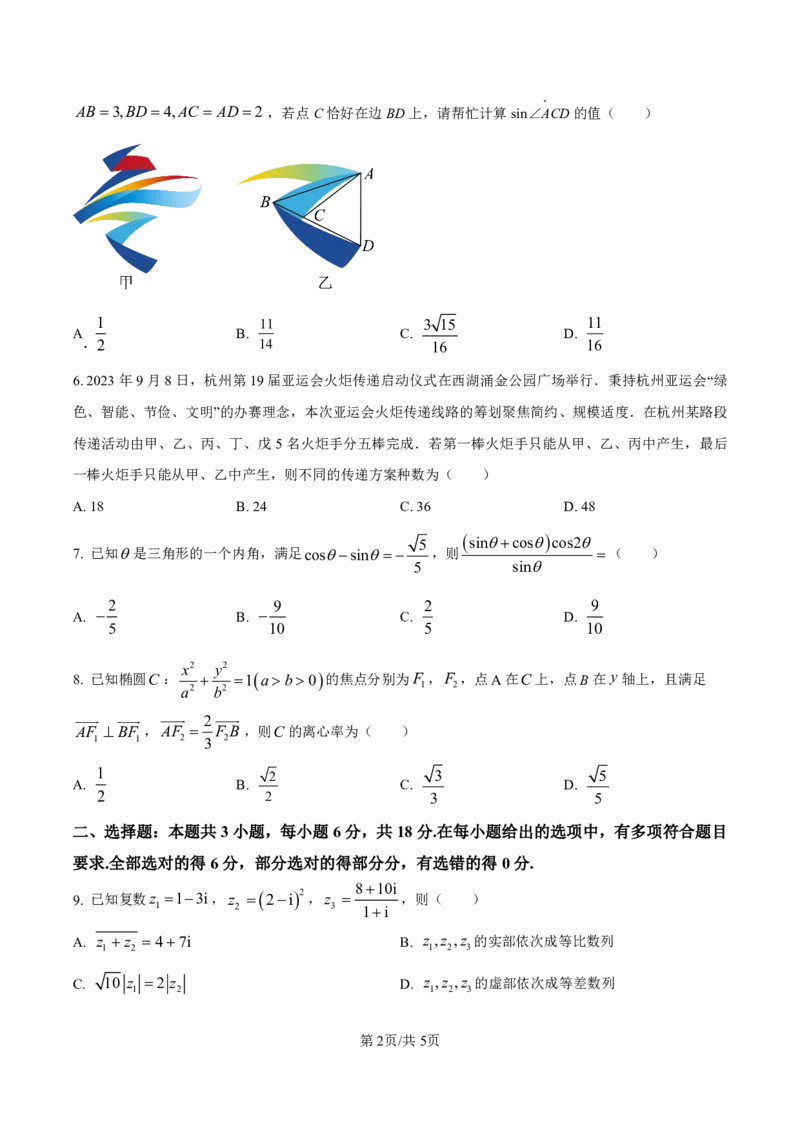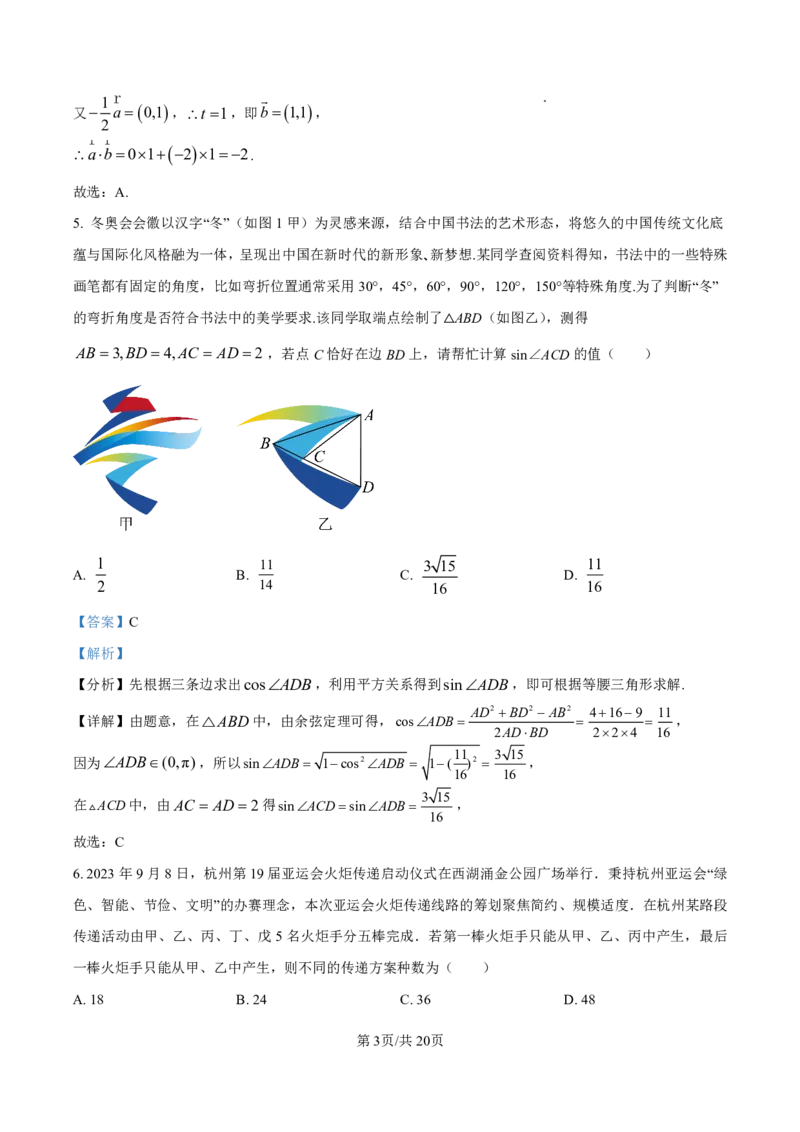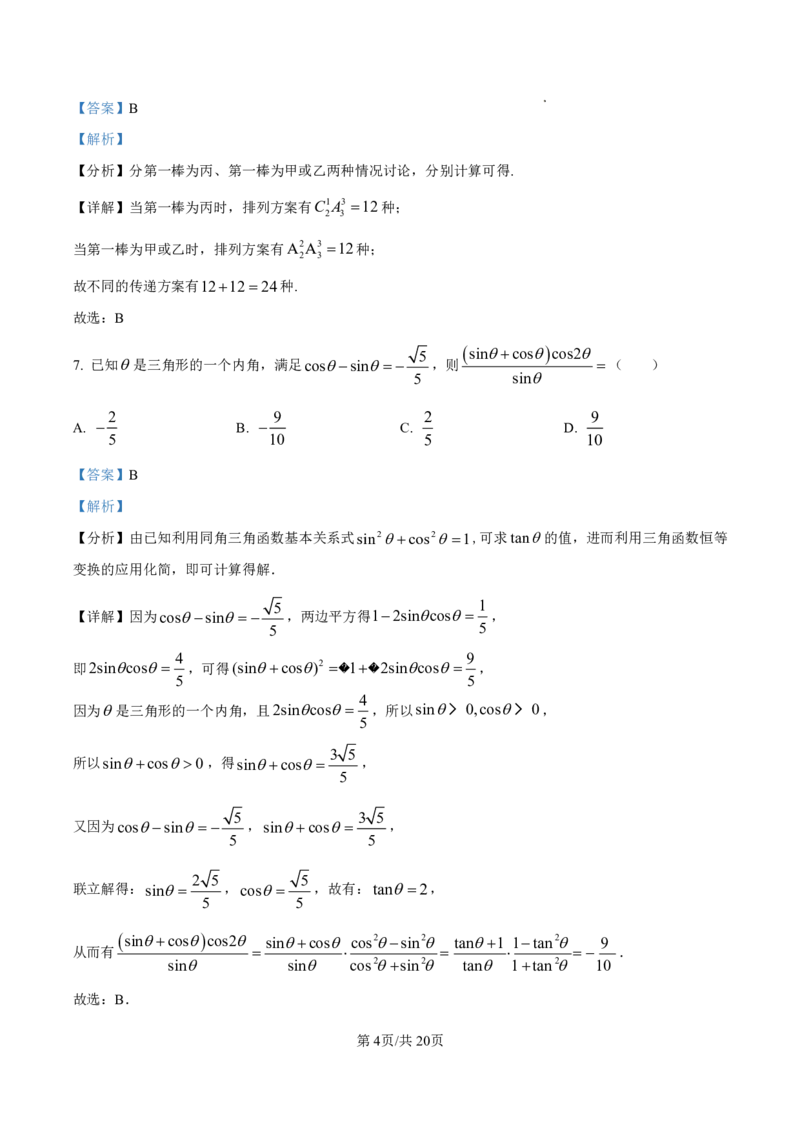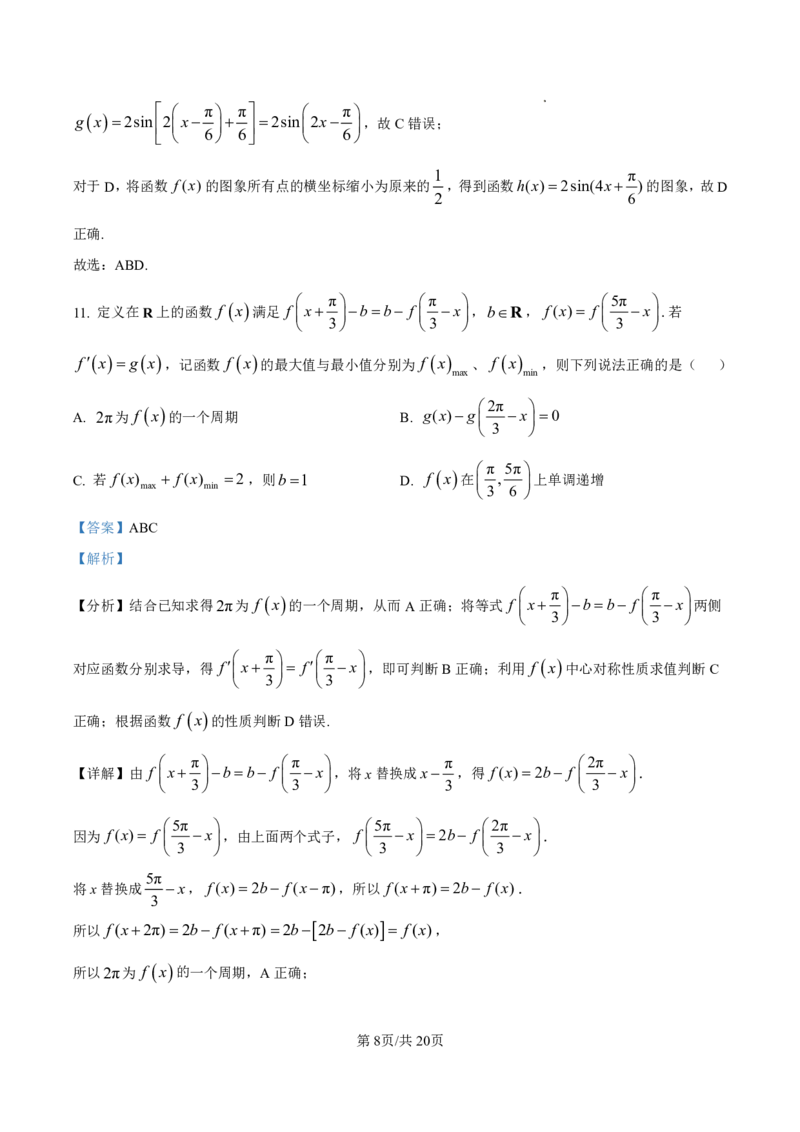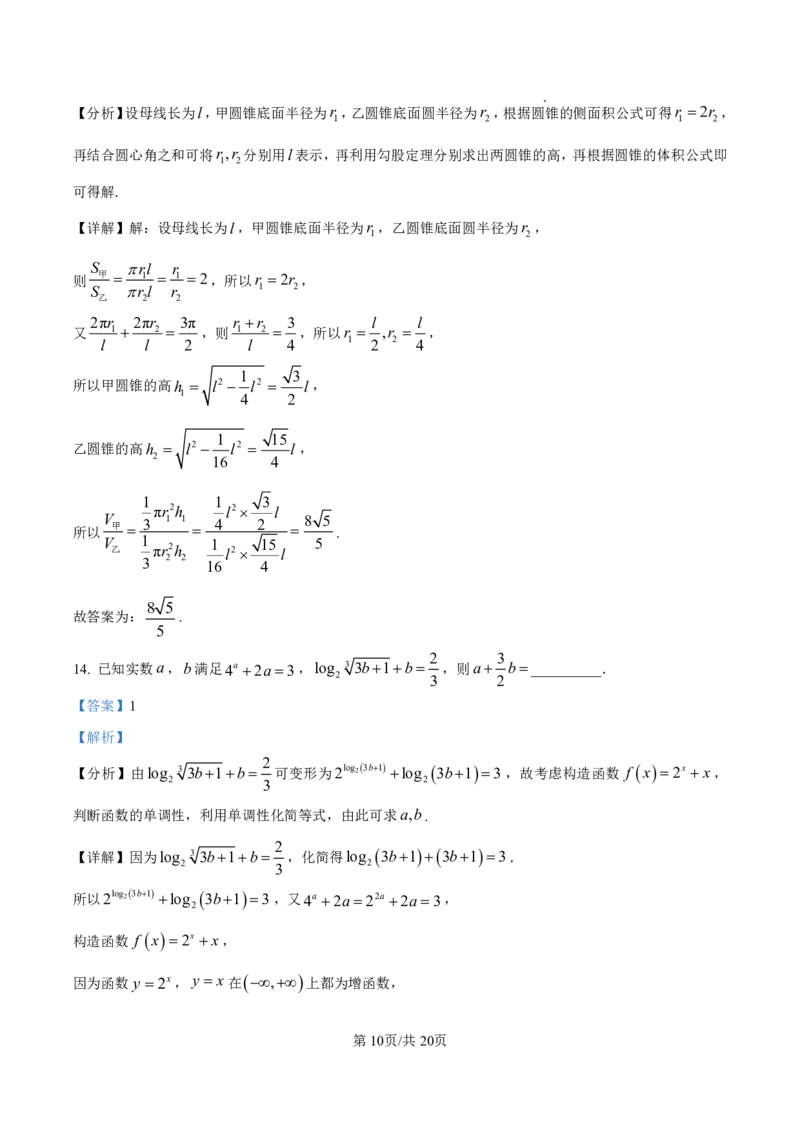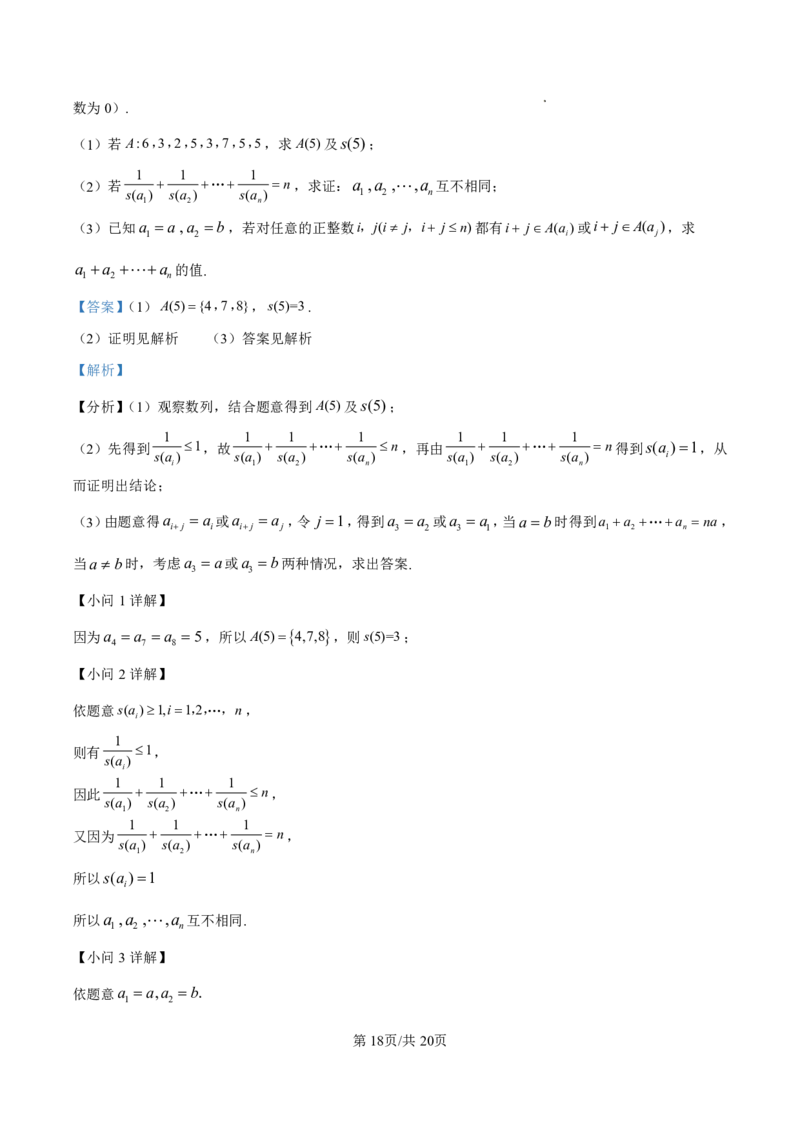2025届河北省沧州市运东五校高三11月期中考-数学试卷+答案_2024-2025高三（6-6月题库）_2024年11月试卷_11262025届河北省沧州市运东五校高三11月期中考

河北省沧州市运东五校 2024-2025 学年高三上学期 11 月期中考试数学
试题
考生注意：
1.本试卷满分 150分，考试时间 120分钟．
2.答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上．
3.请按照题号顺序在各题的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题
卷上答题无效．
4.考试结束后，将本试题卷和答题卡一并上交．
一、选择题：本题共 8小题，每小题5分，共 40分.在每小题给出的四个选项中，只有一项是
符合题目要求的．
1. 某地有8个快递收件点，在某天接收到的快递个数分别为360，284，290，300，188，240，260，288，
则这组数据的上四分位数为（ ）
A.290 B.295 C.300 D.330
2. 已知数列  a  是无穷项等比数列，公比为q，则“q 1”是“数列  a  单调递增”的（ ）
n n
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分又不必要条件
x2 y2
3. 已知圆C:x2  y2 10y210与双曲线  1(a0,b0)的渐近线相切，则该双曲线的离心
a2 b2
率是
5 5
A. 2 B. C. D. 5
3 2
4. 已知向量a   0,2  ，b   1,t ，若向量b  在向量a  上的投影向量为 1 a  ，则a  b  （ ）
2
5 11
A. 2 B.  C.2 D.
2 2
5. 冬奥会会徽以汉字“冬”（如图1甲）为灵感来源，结合中国书法的艺术形态，将悠久的中国传统文化底
蕴与国际化风格融为一体，呈现出中国在新时代的新形象､新梦想.某同学查阅资料得知，书法中的一些特殊
画笔都有固定的角度，比如弯折位置通常采用30°，45°，60°，90°，120°，150°等特殊角度.为了判断“冬”
的弯折角度是否符合书法中的美学要求.该同学取端点绘制了 ABD（如图乙），测得
△
第1页/共5页
学科网（北京）股份有限公司AB 3,BD 4,AC  AD 2 ，若点C恰好在边BD上，请帮忙计算sin∠ACD的值（ ）
1 11 3 15 11
A B. C. D.
. 2 14 16 16
6.2023年9月8日，杭州第19届亚运会火炬传递启动仪式在西湖涌金公园广场举行．秉持杭州亚运会“绿
色、智能、节俭、文明”的办赛理念，本次亚运会火炬传递线路的筹划聚焦简约、规模适度．在杭州某路段
传递活动由甲、乙、丙、丁、戊5名火炬手分五棒完成．若第一棒火炬手只能从甲、乙、丙中产生，最后
一棒火炬手只能从甲、乙中产生，则不同的传递方案种数为（ ）
A.18 B.24 C.36 D.48
5  sincos cos2
7. 已知是三角形的一个内角，满足cossin ，则 （ ）
5 sin
2 9 2 9
A.  B.  C. D.
5 10 5 10
x2 y2
8. 已知椭圆C：  1  ab0 的焦点分别为F ，F ，点A在C上，点B在 y 轴上，且满足
a2 b2 1 2
   2
AF  BF ，AF  F B，则C的离心率为（ ）
1 1 2 3 2
1 2 3 5
A. B. C. D.
2 2 3 5
二、选择题：本题共 3小题，每小题6分，共 18分.在每小题给出的选项中，有多项符合题目
要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分.
810i
9. 已知复数z 13i，z  2i 2，z  ，则（ ）
1 2 3 1i
A. z  z  47i B. z ,z ,z 的实部依次成等比数列
1 2 1 2 3
C. 10 z 2 z D. z ,z ,z 的虚部依次成等差数列
1 2 1 2 3
第2页/共5页
学科网（北京）股份有限公司 π
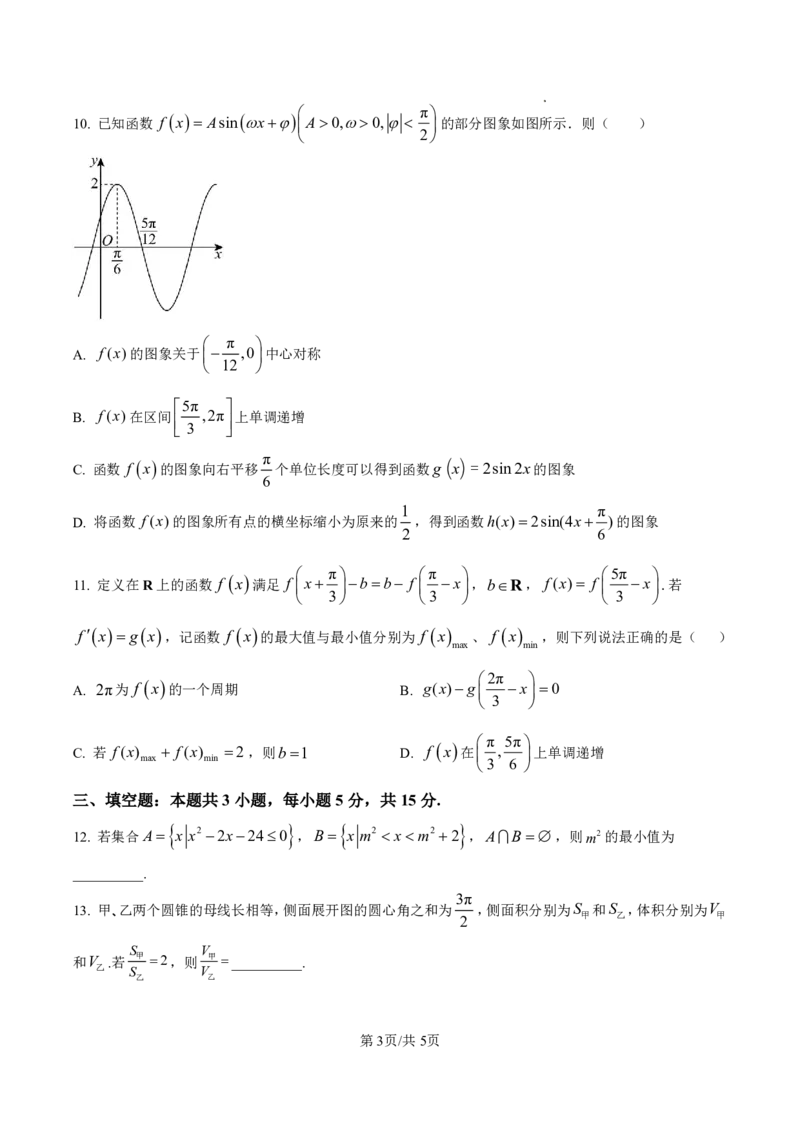
10. 已知函数 f  x  Asin x A0,0, 的部分图象如图所示．则（ ）
 2
 π 
A. f (x)的图象关于  ,0中心对称
 12 
5π 
B. f (x)在区间  ,2π  上单调递增
 3 
C. 函数 f  x  的图象向右平移 π 个单位长度可以得到函数g ( x )=2sin2x的图象
6
1 π
D. 将函数 f (x)的图象所有点的横坐标缩小为原来的 ，得到函数h(x)2sin(4x )的图象
2 6
 π π  5π 
11. 定义在R上的函数 f  x  满足 f x  bb f  x，bR， f(x) f  x.若
 3 3   3 
f
x

g

x

，记函数 f

x

的最大值与最小值分别为 f

x

、 f

x

，则下列说法正确的是（ ）
max min
2π 
A. 2π为 f  x  的一个周期 B. g(x)g x 0
 3 
π 5π
C. 若 f(x)  f(x) 2，则b1 D. f  x  在 , 上单调递增
max min  3 6 
三、填空题：本题共 3小题，每小题 5分，共 15分.
   
12. 若集合A x x22x240 ，B  x m2  xm22 ，AB ，则m2的最小值为
__________.
3π
13. 甲､乙两个圆锥的母线长相等，侧面展开图的圆心角之和为 ，侧面积分别为S 和S ，体积分别为V
甲 乙 甲
2
S V
和V .若 甲 2，则 甲 __________.
乙 S V
乙 乙
第3页/共5页
学科网（北京）股份有限公司2 3
14. 已知实数a，b满足4a 2a3，log 3 3b1b ，则a b__________．
2 3 2
四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤.
a
15 已知函数 f  x  x33x29x
.
3
   
（1）当a 3时，求 f x 在区间 0,4 上的最值；
（2）若直线l:12x y10是曲线 y  f  x 的一条切线，求a的值.
16.“村BA”后，贵州“村超”又火出圈!所谓“村超”，其实是目前火爆全网的贵州乡村体育赛事一一榕
江（三宝侗寨）和美乡村足球超级联赛，被大家简称为“村超”.“村超”的民族风､乡土味､欢乐感，让每
个人尽情享受着足球带来的快乐.
某校为了丰富学生课余生活，组建了足球社团.足球社团为了解学生喜欢足球是否与性别有关，随机抽取了
男､女同学各50名进行调查，部分数据如表所示：
喜欢足球 不喜欢足球 合计
男生 20
女生 15
合计 100
n(ad bc)2
附：2 
.
 ab  cd  ac  bd 

0.1 0.05 0.01 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828

（1）根据所给数据完成上表，依据0.005的独立性检验，能否有99.5%的把握认为该中学学生喜欢足
球与性别有关？
（2）社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范定点射门.据统计，这两名男生进球
第4页/共5页
学科网（北京）股份有限公司2 1
的概率均为 ，这名女生进球的概率为 ，每人射门一次，假设各人进球相互独立，求3人进球总次数X
3 2
的分布列和数学期望.
17. 如图，多面体PSABCD由正四棱锥P ABCD和正四面体S PBC组合而成.
（1）证明：PS //平面ABCD；
（2）求AS与平面PAD所成角的正弦值.
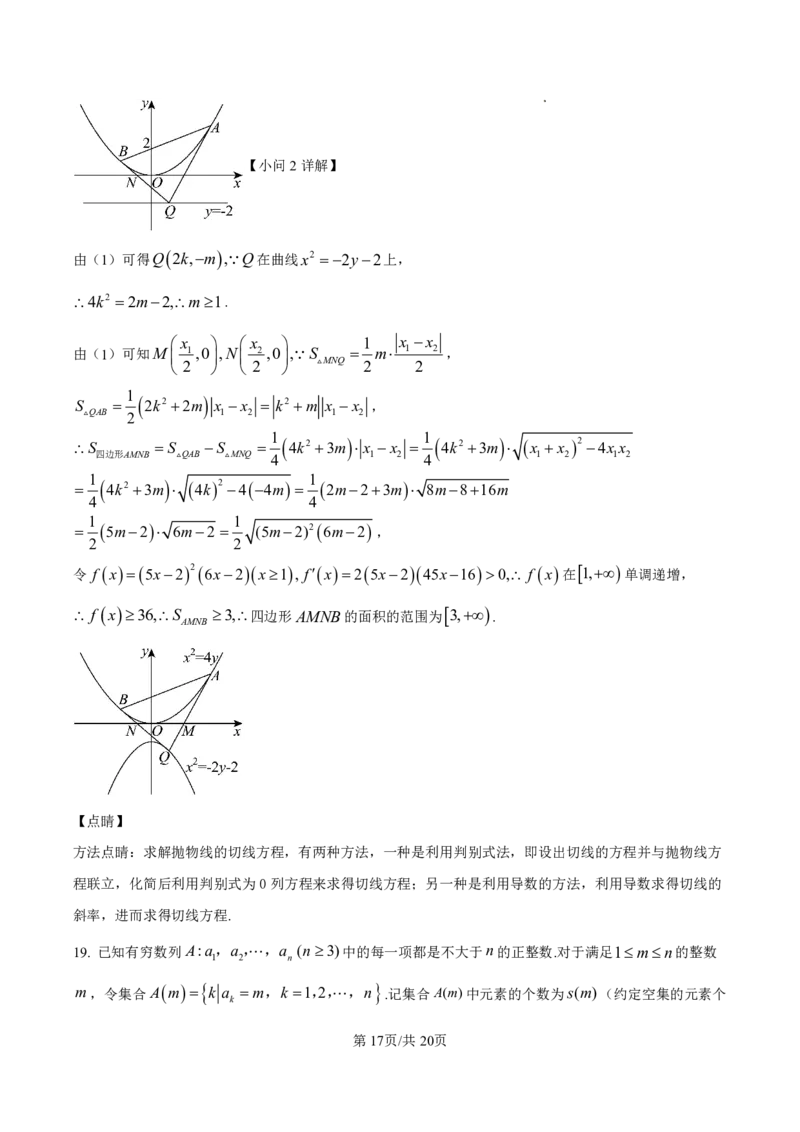
18. 已知抛物线x2 4y,Q为抛物线外一点，过点Q作抛物线的两条切线，切点分别为A,B（A,B在 y 轴
两侧），QA与QB分别交x轴于M,N .
（1）若点Q在直线y=2上，证明直线AB过定点，并求出该定点；
（2）若点Q在曲线x2 2y2上，求四边形AMNB的面积的范围.
19. 已知有穷数列A:a，a ，，a (n3)中的每一项都是不大于n的正整数.对于满足1mn的整数
1 2 n
m，令集合A  m   k a m，k 1，2，，n  .记集合A(m)中元素的个数为s(m)（约定空集的元素个
k
数为0）.
（1）若A:6，3，2，5，3，7，5，5，求A(5)及s(5)；
1 1 1
（2）若   n，求证：a ,a ,,a 互不相同；
s(a ) s(a ) s(a ) 1 2 n
1 2 n
（3）已知a a,a b，若对任意的正整数i，j(i j，i jn)都有i jA(a )或i jA(a )，求
1 2 i j
a a a 的值.
1 2 n
第5页/共5页
学科网（北京）股份有限公司河北省沧州市运东五校 2024-2025 学年高三上学期 11 月期中考试数学
试题
考生注意：
1.本试卷满分 150分，考试时间 120分钟．
2.答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上．
3.请按照题号顺序在各题的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题
卷上答题无效．
4.考试结束后，将本试题卷和答题卡一并上交．
一、选择题：本题共 8小题，每小题5分，共 40分.在每小题给出的四个选项中，只有一项是
符合题目要求的．
1. 某地有8个快递收件点，在某天接收到的快递个数分别为360，284，290，300，188，240，260，288，
则这组数据的上四分位数为（ ）
A.290 B.295 C.300 D.330
【答案】B
【解析】
【分析】根据百分位数的定义计算即可.
【详解】将数据从小到大排序为：188,240,260,284,288,290,300,360;875%6，
290300
所以上四分位数第6个数与第7个数的中位数，为 295.
2
故选:B.
2. 已知数列  a  是无穷项等比数列，公比为q，则“q 1”是“数列  a  单调递增”的（ ）
n n
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分又不必要条件
【答案】D
【解析】
【分析】根据等比数列的首项、公比的不同情形，分析数列的单调性，结合充分条件、必要条件得解.
【详解】若a 0，q 1，则数列  a  单调递减，故q 1不能推出数列  a  单调递增；
1 n n
若  a  单调递增，则a 0，q 1，或a 0，0q1，不能推出q 1，
n 1 1
第1页/共20页
学科网（北京）股份有限公司 
所以“q 1”是“数列 a 单调递增”的既不充分也不必要条件，
n
故选：D．
x2 y2
3. 已知圆C:x2  y2 10y210与双曲线  1(a0,b0)的渐近线相切，则该双曲线的离心
a2 b2
率是
5 5
A. 2 B. C. D. 5
3 2
【答案】C
【解析】
【分析】由双曲线方程，求得其一条渐近线的方程bxay0，再由圆C，求得圆心为C(0,5)，半径r 2，
c 5
利用直线与圆相切，即可求得  ，得到答案．
a 2
x2 y2 b
【详解】由双曲线  1(a0,b0)，可得其一条渐近线的方程为 y  x，即bxay0，
a2 b2 a
又由圆C:x2  y2 10y210，可得圆心为C(0,5)，半径r 2，
5a 5a 5a c 5
则圆心到直线的距离为d   ，则 2，可得e  ，
b2 (a)2 c c a 2
故选C．
【点睛】本题主要考查了双曲线的离心率的求解，以及直线与圆的位置关系的应用，着重考查了推理与运
算能力，属于基础题．
4. 已知向量a   0,2  ，b   1,t ，若向量b  在向量a  上的投影向量为 1 a  ，则a  b  （ ）
2
5 11
A. 2 B.  C.2 D.
2 2
【答案】A
【解析】
【分析】根据向量投影的概念运算求出t，再利用向量数量积运算求得结果.
r r r
r
 
r ab a
  a
【详解】由题b在a上的投影向量为 b cos r  r   0,t  ，
2
a a
第2页/共20页
学科网（北京）股份有限公司r
1 
又 a 0,1 ，t 1，即b 1,1 ，
2
r r
ab012 12.
故选：A.
5. 冬奥会会徽以汉字“冬”（如图1甲）为灵感来源，结合中国书法的艺术形态，将悠久的中国传统文化底
蕴与国际化风格融为一体，呈现出中国在新时代的新形象､新梦想.某同学查阅资料得知，书法中的一些特殊
画笔都有固定的角度，比如弯折位置通常采用30°，45°，60°，90°，120°，150°等特殊角度.为了判断“冬”
的弯折角度是否符合书法中的美学要求.该同学取端点绘制了 ABD（如图乙），测得
AB 3,BD 4,AC  AD 2 ，若点C恰好在边BD上，请△帮忙计算sin∠ACD的值（ ）
1 11 3 15 11
A. B. C. D.
2 14 16 16
【答案】C
【解析】
【分析】先根据三条边求出cosADB，利用平方关系得到sinADB，即可根据等腰三角形求解.
AD2 BD2 AB2 4169 11
【详解】由题意，在△ABD中，由余弦定理可得，cosADB   ，
2ADBD 224 16
11 3 15
因为ADB(0,π)，所以sinADB 1cos2ADB  1( )2  ，
16 16
3 15
在ACD中，由AC  AD  2得sinACDsinADB ，
16
故选：C
6.2023年9月8日，杭州第19届亚运会火炬传递启动仪式在西湖涌金公园广场举行．秉持杭州亚运会“绿
色、智能、节俭、文明”的办赛理念，本次亚运会火炬传递线路的筹划聚焦简约、规模适度．在杭州某路段
传递活动由甲、乙、丙、丁、戊5名火炬手分五棒完成．若第一棒火炬手只能从甲、乙、丙中产生，最后
一棒火炬手只能从甲、乙中产生，则不同的传递方案种数为（ ）
A.18 B.24 C.36 D.48
第3页/共20页
学科网（北京）股份有限公司【答案】B
【解析】
【分析】分第一棒为丙、第一棒为甲或乙两种情况讨论，分别计算可得.
【详解】当第一棒为丙时，排列方案有C1A3 12种；
2 3
当第一棒为甲或乙时，排列方案有A2A3 12种；
2 3
故不同的传递方案有121224种.
故选：B
5  sincos cos2
7. 已知是三角形的一个内角，满足cossin ，则 （ ）
5 sin
2 9 2 9
A.  B.  C. D.
5 10 5 10
【答案】B
【解析】
【分析】由已知利用同角三角函数基本关系式sin2cos21,可求tan的值，进而利用三角函数恒等
变换的应用化简，即可计算得解．
5 1
【详解】因为cossin ，两边平方得12sincos ，
5 5
4 9
即2sincos ，可得(sincos)2 12sincos ，
5 5
4
因为是三角形的一个内角，且2sincos ，所以sin> 0,cos> 0，
5
3 5
所以sincos0，得sincos ，
5
5 3 5
又因为cossin ，sincos ，
5 5
2 5 5
联立解得：sin ，cos ，故有：tan2，
5 5
 sincos cos2 sincos cos2sin2 tan1 1tan2 9
从而有      ．
sin sin cos2sin2 tan 1tan2 10
故选：B．
第4页/共20页
学科网（北京）股份有限公司x2 y2
8. 已知椭圆C：  1  ab0 的焦点分别为F ，F ，点A在C上，点B在 y 轴上，且满足
a2 b2 1 2
   2
AF  BF ，AF  F B，则C的离心率为（ ）
1 1 2 3 2
1 2 3 5
A. B. C. D.
2 2 3 5
【答案】D
【解析】
   2 5 16
【分析】设 Ax ,y ，先根据 AF  BF ， AF  F B 得x  c， y2  c2，代入椭圆方程可得
0 0 1 1 2 3 2 0 3 0 9
5
25e4 50e2 90，进而解方程可得e .
5
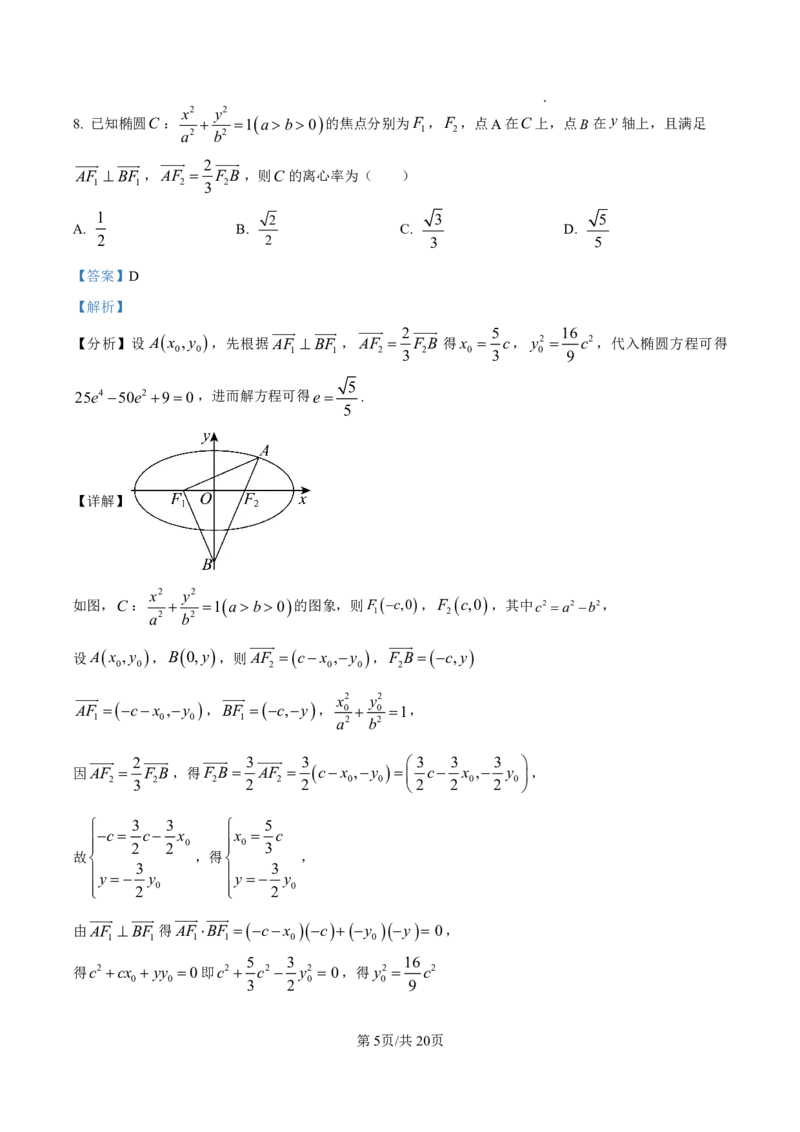
【详解】
如图，C：
x2

y2
1  ab0 的图象，则F c,0，F  c,0  ，其中c2 a2b2，
a2 b2 1 2
 
设Ax ,y ，B  0,y  ，则AF  cx ,y ，F B c,y 
0 0 2 0 0 2
  x2 y2
AF cx ,y ，BF c,y ， 0  0 1，
1 0 0 1 a2 b2
 2  3 3 3 3 3 
因AF  F B，得F B  AF   cx ,y   c x , y ，
2 3 2 2 2 2 2 0 0 2 2 0 2 0 
 3 3  5
c c x x  c
  2 2 0   0 3
故 ，得 ，
3 3
 
y  y y  y
 2 0  2 0
   
由AF  BF 得AF BF cx c y y  0，
1 1 1 1 0 0
5 3 16
得c2 cx  yy 0即c2  c2  y2  0，得 y2  c2
0 0 3 2 0 0 9
第5页/共20页
学科网（北京）股份有限公司2
5  16
x2 y2  c c2 c
由 0  0 1，得 3  9 ，又b2 a2 c2，e ，
a2 b2  1 a
a2 b2
化简得25e4 50e2
90，又椭圆离心率e
0,1

，
1 5
所以e2  ，得e
.
5 5
故选：D
二、选择题：本题共 3小题，每小题6分，共 18分.在每小题给出的选项中，有多项符合题目
要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分.
810i
9. 已知复数z 13i，z  2i 2，z  ，则（ ）
1 2 3 1i
A. z  z  47i B. z ,z ,z 的实部依次成等比数列
1 2 1 2 3
C. 10 z 2 z D. z ,z ,z 的虚部依次成等差数列
1 2 1 2 3
【答案】ABC
【解析】
【分析】由题意由复数乘除法分别将z ,z 化简，再由复数加法、共轭复数的概念即可判断A；复数的实部、
2 3
虚部以及等差数列、等比数列的概念即可判断BD，由复数模的运算即可判断C.
810i  810i  1i 
【详解】因为z  2i 2 34i，z   9i，所以z  z  47i，所以
2 3 1i  1i  1i  1 2
z  z  47i，故A正确；
1 2
因为z ，z ，z 的实部分别为1，3，9，所以z ，z ，z 的实部依次成等比数列，故B正确；
1 2 3 1 2 3
因为z ，z ，z 的虚部分别为3，4，1，所以z ，z ，z 的虚部依次不成等差数列，故D错误；
1 2 3 1 2 3
10 z  10 19 2 z 2510 ，故C正确.
1 2
故选：ABC.
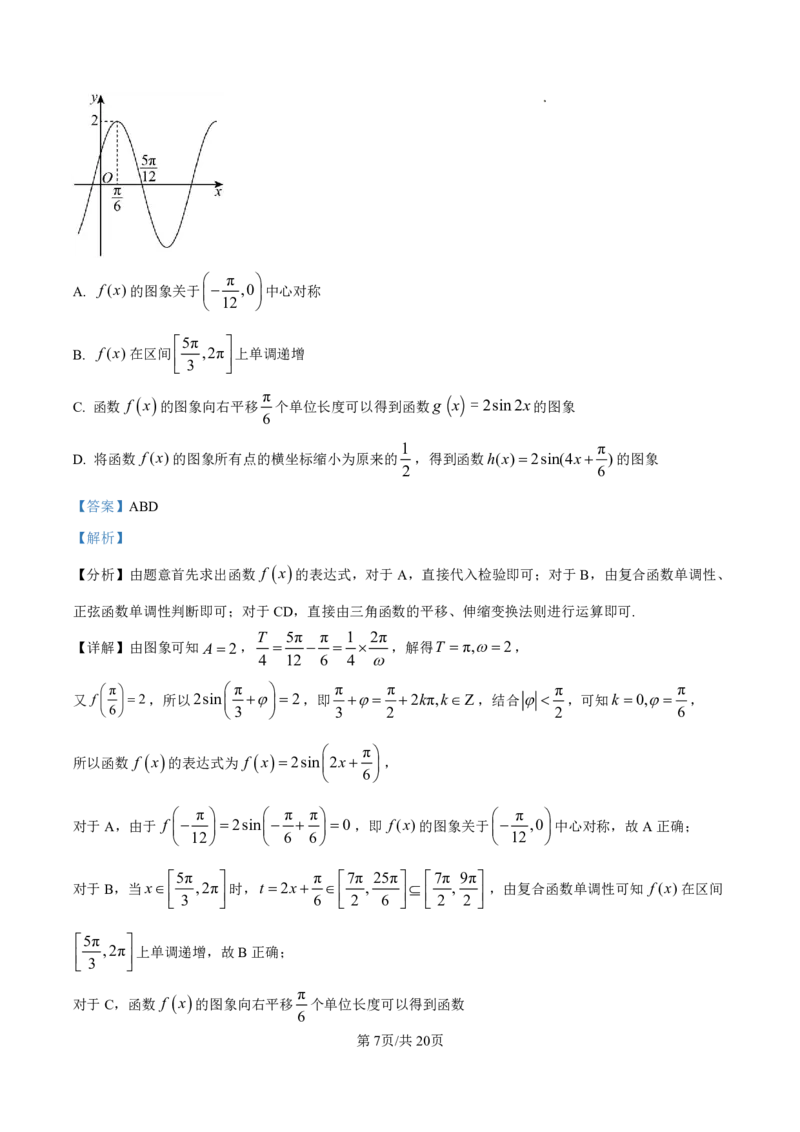
 π
10. 已知函数 f  x  Asin x A0,0, 的部分图象如图所示．则（ ）
 2
第6页/共20页
学科网（北京）股份有限公司 π 
A. f (x)的图象关于  ,0中心对称
 12 
5π 
B. f (x)在区间  ,2π  上单调递增
 3 
C. 函数 f  x  的图象向右平移 π 个单位长度可以得到函数g ( x )=2sin2x的图象
6
1 π
D. 将函数 f (x)的图象所有点的横坐标缩小为原来的 ，得到函数h(x)2sin(4x )的图象
2 6
【答案】ABD
【解析】
 
【分析】由题意首先求出函数 f x 的表达式，对于A，直接代入检验即可；对于B，由复合函数单调性、
正弦函数单调性判断即可；对于CD，直接由三角函数的平移、伸缩变换法则进行运算即可.
T 5π π 1 2π
【详解】由图象可知A2，     ，解得T  π,2，
4 12 6 4 
π π  π π π π
又 f  2，所以2sin   2，即  2kπ,kZ，结合 ，可知k 0, ，
6 3  3 2 2 6
 π
所以函数 f

x

的表达式为 f

x
2sin2x
，
 6
 π   π π  π 
对于A，由于 f     2sin    0，即 f (x)的图象关于  ,0中心对称，故A正确；
 12  6 6  12 
5π  π 7π 25π 7π 9π
对于B，当x

,2π

时，t 2x 

,



,

，由复合函数单调性可知 f (x)在区间
 3  6  2 6   2 2 
5π 

,2π

上单调递增，故B正确；
 3 
π
 
对于C，函数 f x 的图象向右平移 个单位长度可以得到函数
6
第7页/共20页
学科网（北京）股份有限公司  π π  π
g  x 2sin2x    2sin2x ，故C错误；
  6 6  6
1 π
对于D，将函数 f (x)的图象所有点的横坐标缩小为原来的 ，得到函数h(x)2sin(4x )的图象，故D
2 6
正确.
故选：ABD.
 π π  5π 
11. 定义在R上的函数 f  x  满足 f x  bb f  x，bR， f(x) f  x.若
 3 3   3 
f
x

g

x

，记函数 f

x

的最大值与最小值分别为 f

x

、 f

x

，则下列说法正确的是（ ）
max min
2π 
A. 2π为 f  x  的一个周期 B. g(x)g x 0
 3 
π 5π
C. 若 f(x)  f(x) 2，则b1 D. f  x  在 , 上单调递增
max min  3 6 
【答案】ABC
【解析】
 π π 
【分析】结合已知求得2π为 f  x  的一个周期，从而A正确；将等式 f x  bb f  x两侧
 3 3 
 π π 
对应函数分别求导，得 f x   f  x，即可判断B正确；利用 f  x  中心对称性质求值判断C
 3 3 
 
正确；根据函数 f x 的性质判断D错误.
 π π  π 2π 
【详解】由 f x  bb f  x，将x替换成x ，得 f(x)2b f  x．
 3 3  3  3 
5π  5π  2π 
因为 f(x) f  x，由上面两个式子， f  x 2b f  x．
 3   3   3 
5π
将x替换成 x， f(x)2b f(xπ)，所以 f(xπ)2b f(x)．
3
所以 f(x2π)2b f(xπ)2b 2b f(x)  f(x)，
所以2π为 f

x
的一个周期，A正确；
第8页/共20页
学科网（北京）股份有限公司 π π 
将等式 f x  bb f  x两侧对应函数分别求导，
 3 3 
 π π  2π 
得 f x   f  x，即g  x  g x成立，B正确；
 3 3   3 
 π π  π 
满足 f x  bb f  x，即函数图象关于点 ,b中心对称，
 3 3   3 
π 
 
函数 f x 的最大值和最小值点一定存在关于点 ,b中心对称的对应关系，
 3 
f(x)  f(x)
所以 max min b，解得b1，C正确；
2
π 5π
   
已知条件中函数 f x 没有单调性，无法判断 f x 在 , 上是否单调递增，D错误.
 3 6 
故选：ABC．
三、填空题：本题共 3小题，每小题 5分，共 15分.
   
12. 若集合A x x22x240 ，B  x m2  xm22 ，AB ，则m2的最小值为
__________.
【答案】6
【解析】
 
【分析】先求出集合A x 4 x6 ，然后由AB，从而求解.
 
【详解】由x2 2x240，解得4 x6，所以A x 4 x6 ，
因为AB，m2 0，所以m2 6，
所以m2的最小值为6.
故答案为：6.
3π
13. 甲､乙两个圆锥的母线长相等，侧面展开图的圆心角之和为 ，侧面积分别为S 和S ，体积分别为V
甲 乙 甲
2
S V
和V .若 甲 2，则 甲 __________.
乙 S V
乙 乙
8 5 8
【答案】 ## 5
5 5
【解析】
第9页/共20页
学科网（北京）股份有限公司【分析】设母线长为l，甲圆锥底面半径为r ，乙圆锥底面圆半径为r ，根据圆锥的侧面积公式可得r 2r ，
1 2 1 2
再结合圆心角之和可将r,r 分别用l表示，再利用勾股定理分别求出两圆锥的高，再根据圆锥的体积公式即
1 2
可得解.
【详解】解：设母线长为l，甲圆锥底面半径为r ，乙圆锥底面圆半径为r ，
1 2
S rl r
则 甲  1  1  2，所以r 2r ，
S rl r 1 2
乙 2 2
2πr 2πr 3π r r 3 l l
又 1  2  ，则 1 2  ，所以r  ,r  ，
l l 2 l 4 1 2 2 4
1 3
所以甲圆锥的高h  l2  l2  l ，
1 4 2
1 15
乙圆锥的高h  l2  l2  l ，
2 16 4
1 1 3
πr2h l2 l
所以 V 甲  3 1 1  4 2  8 5 .
V 乙 1 πr2h 1 l2 15 l 5
3 2 2 16 4
8 5
故答案为： .
5
2 3
14. 已知实数a，b满足4a 2a3，log 3 3b1b ，则a b__________．
2 3 2
【答案】1
【解析】
2
【分析】由log 3 3b1b 可变形为2log 2 3b1 log  3b1 3 ，故考虑构造函数 f  x 2x x，
2 3 2
判断函数的单调性，利用单调性化简等式，由此可求a,b.
2
【详解】因为log 3 3b1b ，化简得log  3b1  3b1 3．
2 3 2
所以2log 2 3b1 log  3b1 3 ，又4a 2a22a 2a3，
2
构造函数 f  x 2x x，
因为函数 y 2x， y  x在 , 上都为增函数，
第10页/共20页
学科网（北京）股份有限公司所以函数 f

x

在
,
上为单调递增函数，
由 f 13，∴2a log  3b1 1，
2
1 1
解得a  ，b ，
2 3
3
∴a b1．
2
故答案为：1.
四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤.
a
15 已知函数 f  x  x33x29x
.
3
   
（1）当a 3时，求 f x 在区间 0,4 上的最值；
（2）若直线l:12x y10是曲线 y  f  x  的一条切线，求a的值.
【答案】（1） f  x  27， f  x  0
min max
（2）a 3
【解析】
【分析】（1）求导后，根据
f
x

正负可确定 f

x

在

0,4

上的单调性，由单调性可确定最值点并求得最
值；
 a 
（2）设切点为x , x3 3x2 9x ，结合切线斜率可构造方程组求得x 和a的值.
 0 3 0 0 0  0
【小问1详解】
当a 3时， f  x  x3 3x2 9x，则 f x 3x2 6x93  x3  x1  ，
当x 0,3 时， fx0；当x 3,4  时， fx0；
\ f ( x )在  0,3  上单调递减，在  3,4  上单调递增，
 f  x   f  3 27， f  x  max  f  0  , f  4  ，
min max
又 f  0 0， f  4 64483620 ， f  x  0.
max
【小问2详解】
由题意知： f x ax2 6x9，
第11页/共20页
学科网（北京）股份有限公司 a 
设直线l与 f  x  相切于点x , x3 3x2 9x ，
 0 3 0 0 0 
ax2 6x 912
 0 0
则a ，消去a得：x2 2x 10，解得：x 1，

x3 3x2 9x 112x 0 0 0
3 0 0 0 0
则a6912，解得：a 3.
16.“村BA”后，贵州“村超”又火出圈!所谓“村超”，其实是目前火爆全网的贵州乡村体育赛事一一榕
江（三宝侗寨）和美乡村足球超级联赛，被大家简称为“村超”.“村超”的民族风､乡土味､欢乐感，让每
个人尽情享受着足球带来的快乐.
某校为了丰富学生课余生活，组建了足球社团.足球社团为了解学生喜欢足球是否与性别有关，随机抽取了
男､女同学各50名进行调查，部分数据如表所示：
喜欢足球 不喜欢足球 合计
男生 20
女生 15
合计 100
n(ad bc)2
附：2 
.
 ab  cd  ac  bd 

0.1 0.05 0.01 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828

（1）根据所给数据完成上表，依据0.005的独立性检验，能否有99.5%的把握认为该中学学生喜欢足
球与性别有关？
（2）社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范定点射门.据统计，这两名男生进球
第12页/共20页
学科网（北京）股份有限公司2 1
的概率均为 ，这名女生进球的概率为 ，每人射门一次，假设各人进球相互独立，求3人进球总次数X
3 2
的分布列和数学期望.
【答案】（1）有99.5%的把握认为该中学学生喜欢足球与性别有关
11
（2）分布列见解析，E  X 
6
【解析】
【分析】（1）根据男女生各 名及表中数据即可填写22列联表，然后根据计算
100 30351520 502
2  从而求解.
50504555
（2）根据题意可知X 的所有可能取值为0,1,2,3，列出分布列，计算出期望从而求解.
【小问1详解】
依题意，22列联表如下：
喜欢足球 不喜欢足球 合计
男生 30 20 50
女生 15 35 50
合计 45 55 100
零假设H ：该中学学生喜欢足球与性别无关，
0
100 30351520 2 100
2的观测值为2    9.091，
50504555 11
9.0917.879 x ，根据小概率值0.005的独立性检验，推断H 不成立，
0.005 0
所以有99.5%的把握认为该中学学生喜欢足球与性别有关.
【小问2详解】
依题意，X 的所有可能取值为0,1,2,3，
2 2
 2  1 1 2 2  1  2 1 5
P  X 0  1   1   ,P  X 1 C1  1   1   1    ，
 3  2 18 2 3 3  2  3 2 18
第13页/共20页
学科网（北京）股份有限公司2 2
2 2 1 2  1 8 4 2 1 2
P  X 2 C1  1       1    ,P  X 3     
2 3 3 2 3  2 18 9 3 2 9
所以X 的分布列为：
X 0 1 2 3
1 5 4 2
P
18 18 9 9
1 5 4 2 11
数学期E  X 0 1 2 3  .
18 18 9 9 6
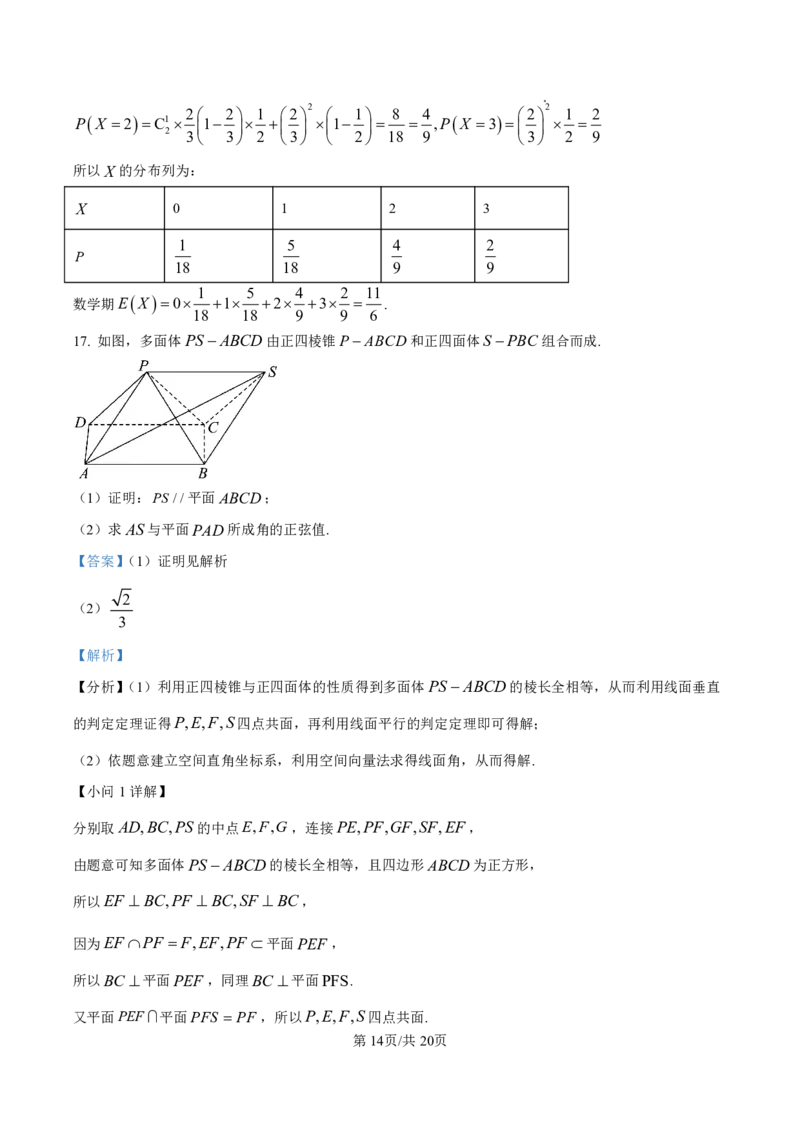
17. 如图，多面体PSABCD由正四棱锥P ABCD和正四面体S PBC组合而成.
（1）证明：PS //平面ABCD；
（2）求AS与平面PAD所成角的正弦值.
【答案】（1）证明见解析
2
（2）
3
【解析】
【分析】（1）利用正四棱锥与正四面体的性质得到多面体PSABCD的棱长全相等，从而利用线面垂直
的判定定理证得P,E,F,S四点共面，再利用线面平行的判定定理即可得解；
（2）依题意建立空间直角坐标系，利用空间向量法求得线面角，从而得解.
【小问1详解】
分别取AD,BC,PS的中点E,F,G，连接PE,PF,GF,SF,EF，
由题意可知多面体PSABCD的棱长全相等，且四边形ABCD为正方形，
所以EF BC,PF BC,SF BC，
因为EFPF  F,EF,PF 平面PEF ，
所以BC 平面PEF ，同理BC 平面PFS.
又平面PEF平面PFS  PF ，所以P,E,F,S四点共面.
第14页/共20页
学科网（北京）股份有限公司又因为EF  ABPS,PE  PF SF，所以四边形PEFS 为平行四边形，
所以PS //EF ，又EF 平面ABCD,PS 平面ABCD，
所以PS //平面ABCD.
【小问2详解】
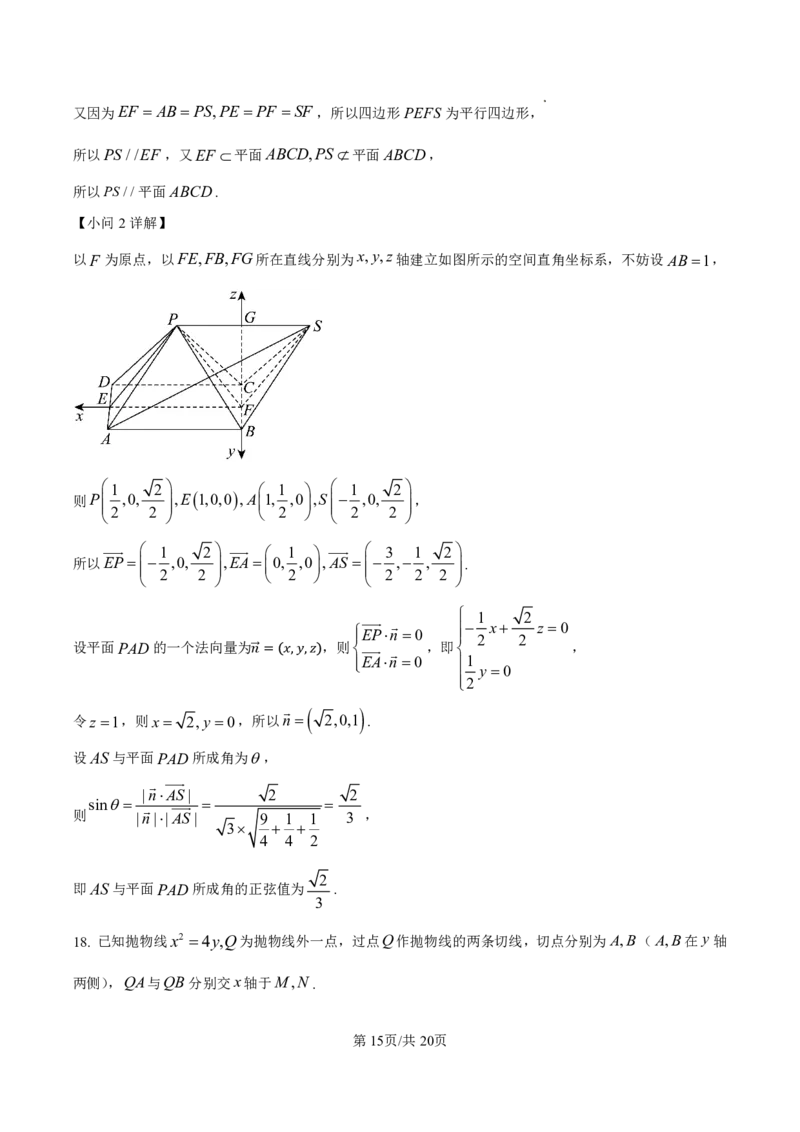
以F 为原点，以FE,FB,FG所在直线分别为x,y,z轴建立如图所示的空间直角坐标系，不妨设AB 1，
1 2   1   1 2 
则P

,0, 

,E  1,0,0  ,A1, ,0,S

 ,0, 

，
2 2   2   2 2 
  1 2    1    3 1 2 
所以EP 

 ,0, 

,EA 0, ,0,AS 

 , , 

.
 2 2   2   2 2 2 
 1 2

 EPn  0    x z  0
2 2
设平面PAD的一个法向量为 ，则 ，即 ，

EAn 0 1
y 0
  =  ,  ,  2
  
令z 1，则x 2,y 0，所以n  2,0,1 .
设AS与平面PAD所成角为，


|nAS| 2 2
sin   

则 |n|| AS| 9 1 1 3 ，
3  
4 4 2
2
即AS与平面PAD所成角的正弦值为 .
3
18. 已知抛物线x2 4y,Q为抛物线外一点，过点Q作抛物线的两条切线，切点分别为A,B（A,B在 y 轴
两侧），QA与QB分别交x轴于M,N .
第15页/共20页
学科网（北京）股份有限公司（1）若点Q在直线y=2上，证明直线AB过定点，并求出该定点；
（2）若点Q在曲线x2 2y2上，求四边形AMNB的面积的范围.
 
【答案】（1）证明见解析，定点 0,2
（2）
 3,
【解析】
【分析】（1）设出直线AB的方程并与抛物线方程联立，化简写出根与系数关系，结合A,B处的切线方程
求得直线AB所过定点.
（2）先求得四边形AMNB的面积的表达式，然后利用导数求得面积的取值范围.
【小问1详解】
设A  x ,y  ,B  x ,y  ,Q  x ,y  ，直线l :y kxm，
1 1 2 2 0 0 AB
x2 4y
联立 ，可得x2 4kx4m0,Δ16k2 16m.
y kxm
A,B在 y 轴两侧，x x 0,m0,Δ0，
1 2
x x 4k,x x 4m，
1 2 1 2
1 1
由x2 4y得y  x2,y x，
4 2
1 1 1
所以A点处的切线方程为 y y  x  xx  ,y x2  x  xx ，
1 2 1 1 4 1 2 1 1
x x x2
整理得 y  1  1 ，
2 4
x x x2
同理可求得B点处的切线方程为 y  2  2 ，
2 4
 x x x2  x x
  y  2 1  4 1   x 0  1 2 2  2k
由 ，可得 ，
 x x x2  x x
y  2  2 y  1 2 m
 2 4  0 4
又Q在直线 y=2上，m2,m2.
直线AB过定点 .
0,2
第16页/共20页
学科网（北京）股份有限公司【小问2详解】
由（1）可得Q  2k,m  ,Q在曲线x2 2y2上，
4k2 2m2,m1.
 x   x  1 x x
由（1）可知M 1,0,N 2 ,0,S  m 1 2 ，
 2   2  MNQ 2 2
1 
S  2k2 2m x x  k2 m x x ，
QAB 2 1 2 1 2
S  S S  1 4k2 3m   x x  1 4k2 3m    x x 2 4x x
四边形AMNB QAB MNQ 4 1 2 4 1 2 1 2
 1 4k2 3m    4k 2 4 4m   1  2m23m  8m816m
4 4
1 1
  5m2  6m2  (5m2)2 6m2  ，
2 2
令 f  x  5x2 2 6x2  x1  , f x 2  5x2  45x16 0, f  x 在  1,单调递增，
 f  x 36,S 3,四边形AMNB的面积的范围为  3, .
AMNB
【点睛】
方法点睛：求解抛物线的切线方程，有两种方法，一种是利用判别式法，即设出切线的方程并与抛物线方
程联立，化简后利用判别式为0列方程来求得切线方程；另一种是利用导数的方法，利用导数求得切线的
斜率，进而求得切线方程.
19. 已知有穷数列A:a，a ，，a (n3)中的每一项都是不大于n的正整数.对于满足1mn的整数
1 2 n
m，令集合A  m   k a m，k 1，2，，n  .记集合A(m)中元素的个数为s(m)（约定空集的元素个
k
第17页/共20页
学科网（北京）股份有限公司数为0）.
（1）若A:6，3，2，5，3，7，5，5，求A(5)及s(5)；
1 1 1
（2）若   n，求证：a ,a ,,a 互不相同；
s(a ) s(a ) s(a ) 1 2 n
1 2 n
（3）已知a a,a b，若对任意的正整数i，j(i j，i jn)都有i jA(a )或i jA(a )，求
1 2 i j
a a a 的值.
1 2 n
【答案】（1）A(5){4，7，8}，s(5)=3.
（2）证明见解析 （3）答案见解析
【解析】
【分析】（1）观察数列，结合题意得到A(5)及s(5)；
1 1 1 1 1 1 1
（2）先得到 1，故   n，再由   n得到s(a )1，从
s(a ) s(a ) s(a ) s(a ) s(a ) s(a ) s(a ) i
i 1 2 n 1 2 n
而证明出结论；
（3）由题意得a a 或a a ，令 j 1，得到a a 或a a ，当a b时得到a a a na，
ij i ij j 3 2 3 1 1 2 n
当a b时，考虑a a或a b两种情况，求出答案.
3 3
【小问1详解】
因为a a a  5，所以A(5)4,7,8，则s(5)=3；
4 7 8
【小问2详解】
依题意s(a)1,i1，2，，n，
i
1
则有 1，
s(a )
i
1 1 1
因此   n，
s(a ) s(a ) s(a )
1 2 n
1 1 1
又因为   n，
s(a ) s(a ) s(a )
1 2 n
所以s(a )1
i
所以a ,a ,,a 互不相同.
1 2 n
【小问3详解】
依题意a a,a b.
1 2
第18页/共20页
学科网（北京）股份有限公司由i jA(a )或i jA(a )，知a a 或a a .
i j ij i ij j
令 j 1，可得a a 或a a ，对于i2,3,...n1成立，
i1 i i1 1
故a a 或a a .
3 2 3 1
①当a b时，
a a a a，
3 4 n
所以a a a na.
1 2 n
②当a b时，
a a或a b.
3 3
当a a时，由a a 或a a ，有a a，
3 4 3 4 1 4
同理a a a a，
5 6 n
所以a a a (n1)ab.
1 2 n
当a b时，此时有a a b，
3 2 3
令i1，j3，可得4A(a)或4A(b)，即a a或a b.
4 4
令i1，j4，可得5A(a)或5A(b). 令i2，j3，可得5A(b).
所以a b.
5
若a a，则令i1，j4，可得a a，与a b矛盾.
4 5 5
所以有a b.
4
不妨设a a a b(k 5)，
2 3 k
令it，jk1t(t 2,3,,k1)，可得k1A(b)，因此a b.
k1
令i 1, j k ，则a a或a b.
k1 k1
故a b.
k1
所以a a a (n1)ba.
1 2 n
综上，a b时，a a a na.
1 2 n
第19页/共20页
学科网（北京）股份有限公司a ab时，a a a (n1)ab.
3 1 2 n
a ba时，a a a (n1)ba.
3 1 2 n
【点睛】数列新定义问题的方法和技巧：
（1）可通过举例子的方式，将抽象的定义转化为具体的简单的应用，从而加深对信息的理解；
（2）可用自己的语言转述新信息所表达的内容，如果能清晰描述，那么说明对此信息理解的较为透彻；
（3）发现新信息与所学知识的联系，并从描述中体会信息的本质特征与规律；
（4）如果新信息是课本知识的推广，则要关注此信息与课本中概念的不同之处，以及什么情况下可以使用
书上的概念，要将“新”性质有机地应用到“旧”性质上，创造性的解决问题.
第20页/共20页
学科网（北京）股份有限公司