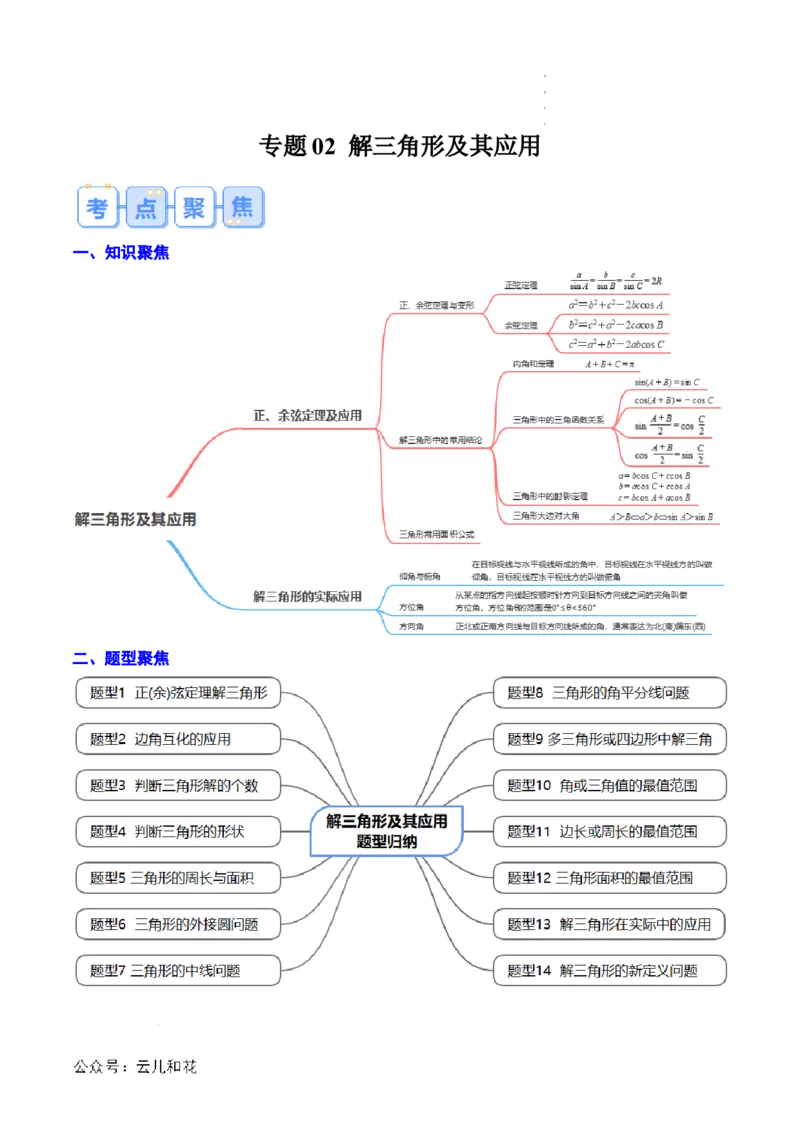
文档内容
专题 02 解三角形及其应用
一、知识聚焦
二、题型聚焦
学科网(北京)股份有限公司 学科网(北京)股份有限公司知识点 1:正、余弦定理及应用
1、正、余弦定理与变形
定理 正弦定理 余弦定理
a2=b2+c2-2bccos A;
内容 ===2R b2=c2+a2-2cacos B;
c2=a2+b2-2abcos C
(1)a=2Rsin A,b=2Rsin B,c=2Rsin
cos A=;
C;
变形 cos B=;
(2)a∶b∶c=sin A∶sin B∶sin C;
cos C=
(3)==2R
【注意】若已知两边和其中一边的对角,解三角形时,可用正弦定理.在根据另一边所对角的正弦值确定
角的值时,要注意避免增根或漏解,常用的基本方法就是注意结合“大边对大角,大角对大边”及三角形
内角和定理去考虑问题.
2、解三角形中的常用结论
(1)三角形内角和定理:在△ABC中,A+B+C=π;变形:=-.
(2)三角形中的三角函数关系
①sin(A+B)=sin C; ②cos(A+B)=-cos C; ③sin =cos ; ④cos =sin .
(3)三角形中的射影定理:在△ABC中,a=bcos C+ccos B;b=acos C+ccos A;c=bcos A+acos B.
(4)三角形中的大角对大边:在△ABC中,A>B a>b sin A>sin B.
3、三角形常用面积公式
⇔ ⇔
(1)S=a·h(h 表示边a上的高);
a a
(2)S=absin C=acsin B=bcsin A;
(3)S=r(a+b+c)(r为内切圆半径).
知识点2:解三角形的实际应用
名称 意义 图形表示
在目标视线与水平视线所成的角中,目
仰角与俯角 标视线在水平视线方的叫做仰角,目标
视线在水平视线方的叫做俯角
从某点的指方向线起按顺时针方向到目
方位角
标方向线之间的夹角叫做方位角,方位
学科网(北京)股份有限公司 学科网(北京)股份有限公司角θ的范围是0°≤θ<360°
例:(1)北偏东α: (2)南偏西
α:
正北或正南方向线与目标方向线所成的
方向角
角,通常表达为北(南)偏东(西)
【注意】(1)方位角和方向角本质上是一样的,方向角是方位角的一种表达形式,是同一问题中对角的
不同描述.
(2)将三角形的解还原为实际问题时,要注意实际问题中的单位、近似值要求,同时还要注意所求的结
果是否符合实际情况.
题型归纳
【题型1 正(余)弦定理解三角形】
满分技法
解三角时,正余弦定理的选择:
(1)已知两角及一边,求其余的边或角,利用正弦定理;
(2)已知两边及其一边的对角,求另一边所对的角,利用正弦定理;
(3)已知两边及其夹角,求第三边,利用余弦定理;
(4)已知三边求角或角的余弦值,利用余弦定理的推论;
(5)已知两边及其一边的对角,求另一边,利用余弦定理;
1.(23-24高一下·湖南·期中)在 中,角 所对的边分别为 .若 ,则
( )
A.2 B.4 C.16 D.
【答案】B
【解析】在 中, ,
由余弦定理得 ,解得 .故选:B.
2.(23-24高一下·广东广州·期中)在 中, , , ,则角 的值为
( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. B. 或 C. D.
【答案】C
【解析】由正弦定理 ,可得 ,
且 ,可知角 的值为 .故选:C.
3.(23-24高一下·湖北·月考) 中,角A,B,C所对的边分别为 已知 ,
则 ( )
A. B. C. D.
【答案】B
【解析】在 中,因为 ,则 ,
由正弦定理 ,可得 .故选:B.
4.(23-24高一下·重庆·期中) 的内角 所对边分别为 ,若 ,则角 的
大小( )
A. B. C. D.
【答案】D
【解析】由余弦定理得, ,
因为 ,所以 ,
由 ,所以 ,故选:D.
【题型2 边角互化的应用】
满分技法
边化角是正弦定理齐次比例关系非常重要的应用,其主要特点是将混有边角关系的条件问题转化为三角恒
等变换问题,并从角的角度来审视三角形的特征,要熟练掌握边化角的三角形考题的特征,一般来说,当条
学科网(北京)股份有限公司 学科网(北京)股份有限公司件中含有特殊数,如 (往往和特殊角有关)或者齐次特征明显时,常进行边化角处理对于正弦定理与三角
恒等变换的综合问题,大多是基于三角形内角和定理展开的,故一般有两种类型:一是利用相应半角的互
余关系、角的互补关系研究三角恒等变换,进而达到减元的目的,也就可以盯着目标进行三角恒等变换:二
是利用正弦定理求得相应的角或者寻找相应的边角关系,进而运用三角恒等变换转化为一个角的三角函数
问题,
5.(23-24高一下·甘肃天水·期中)在△ABC中,角A,B,C所对的边分别为a,b,c,且
, ,则( )
A. B. C. D.
【答案】B
【解析】由 得 ,
由于 ,所以 ,故 ,故选:B
6.(23-24高一下·湖北武汉·期中)已知 的内角 , , 的对边分别为 , , ,且
, ,则 ( )
A. B. C. D.
【答案】D
【解析】因为 ,所以 ,
整理可得 ①,
又 ,
可得 ,
所以 ,解得 ②,
由①②可得 ,所以 ,
则 .故选:D
7.(23-24高一下·四川眉山·月考)在 中,角 所对的边分别为 ,已知
学科网(北京)股份有限公司 学科网(北京)股份有限公司,且 ,则 ( )
A. B. C. D.
【答案】D
【解析】由正弦定理可得: ,
所以由余弦定理可得: ,
所以 ,再由正弦定理可得: .故选:D.
8.(23-24高一下·广西钦州·期中)设 的内角 的对边分别为 若 的周长为
则( )
A. B. C. D.
【答案】A
【解析】由题意可知 ,
由正弦定理得
即 整理得
由余弦定理得
又 所以 故选:A.
【题型3 判断三角形解的个数】
满分技法
1、从代数上来说,可由“大边对大角”来判断;
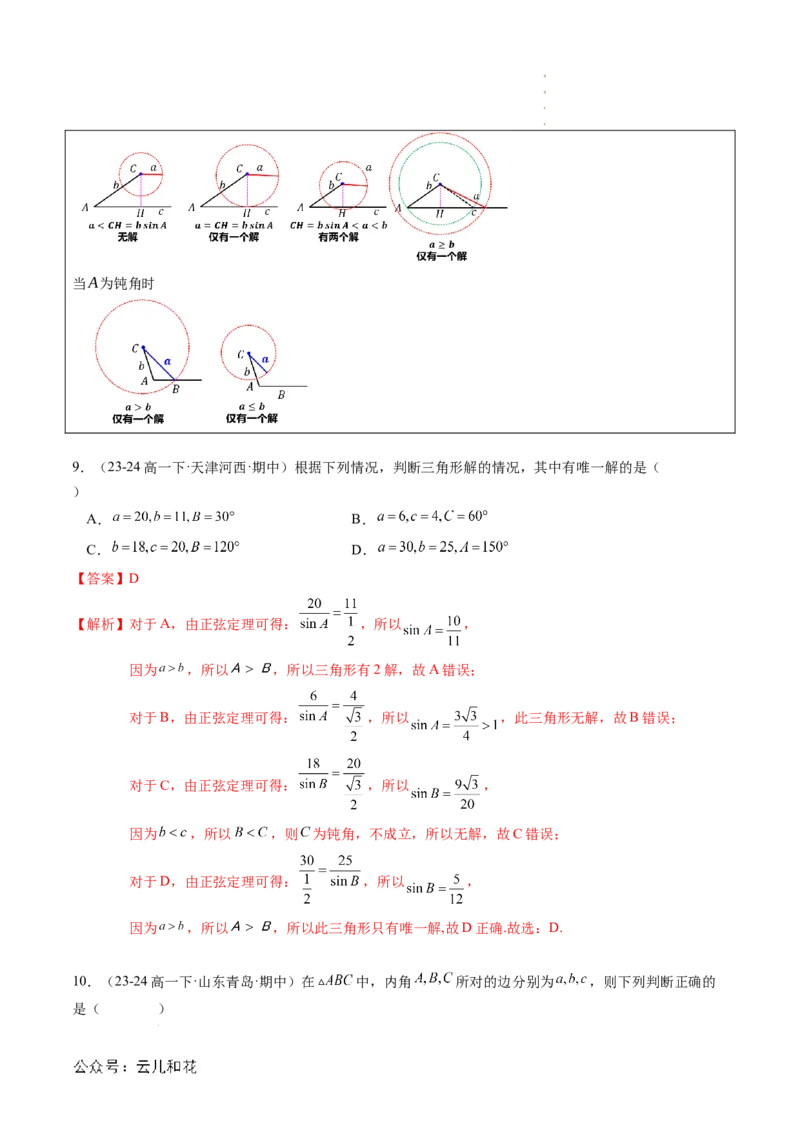
2、从几何上来说,已知两边及一边对角,解三角形(三角形多解问题)
在△ABC中,已知a,b和A时,解的情况如下:
当A为锐角时:
学科网(北京)股份有限公司 学科网(北京)股份有限公司当A为钝角时
9.(23-24高一下·天津河西·期中)根据下列情况,判断三角形解的情况,其中有唯一解的是(
)
A. B.
C. D.
【答案】D
【解析】对于A,由正弦定理可得: ,所以 ,
因为 ,所以 ,所以三角形有2解,故A错误;
对于B,由正弦定理可得: ,所以 ,此三角形无解,故B错误;
对于C,由正弦定理可得: ,所以 ,
因为 ,所以 ,则 为钝角,不成立,所以无解,故C错误;
对于D,由正弦定理可得: ,所以 ,
因为 ,所以 ,所以此三角形只有唯一解,故D正确.故选:D.
10.(23-24高一下·山东青岛·期中)在 中,内角 所对的边分别为 ,则下列判断正确的
是( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. , , ,有两解 B. , , ,有一解
C. , , ,有一解 D. , , ,无解
【答案】D
【解析】选项A:因为 ,故 只有一解,故A错误;
选项B:因 ,故 有两解,故B错误;
选项C:因 ,故 有两解,故C错误;
选项D:因 ,故 无解,故D正确.故选:D
11.(23-24高一下·福建三明·期中)在 中, , , ,若满足条件的 有且仅有
一个,则 的取值范围是( )
A. B. C. D.
【答案】A
【解析】由正弦定理 ,则 ,即 ,由题意 仅有一值,
故 或 ,解得 或 .故选:A
12.(23-24高一下·黑龙江哈尔滨·期中)在 中, , ,满足此条件 有两解,
则BC边长度的取值范围为( )
A. B. C. D.
【答案】D
【解析】∵ 有两解,
∴ ,∴ ,故选:D.
【题型4 判断三角形的形状】
满分技法
判断三角形形状的两种途径
1、角化边:利用正弦定理、余弦定理化角为边,通过代数恒等变换,求出边与边之间的关系进行判断;
2、边化角:通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断.
13.(23-24高一下·重庆·期中)在 中,内角 所对边分别为 ,若 ,则
的形状是( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等腰或直角三角形
【答案】B
【解析】因为
所以 ,整理得 ,
即 的形状是等腰三角形.故选:B.
14.(23-24高一下·安徽宿州·期中)在 中,内角 的对边分别为 若满足 ,则
该三角形为( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.不能确定
【答案】B
【解析】在 中,已知
由正弦定理得 ,
所以 即
又 ,则 ,则 ,
所以 所以该三角形为等腰三角形.故选:B.
15.(23-24高一下·福建福州·期中)在 中,角 所对的边分别为 ,若 ,则
的形状为( )
A.正三角形 B.直角三角形 C.等腰三角形 D.钝角三角形
【答案】B
【解析】由 得 ,
即 ,
即 ,
所以 ,
在 中, ,所以 , ,
即 的形状为直角三角形.故选:B.
16.(23-24高一下·陕西西安·期中)(多选)在 中,角 的对边分别为 ,下列四个命题
中正确的是( )
A.若 则 是等腰三角形
学科网(北京)股份有限公司 学科网(北京)股份有限公司B.若 ,则 为锐角三角形
C.若 ,则 一定是等边三角形
D.若 ,则 一定是等腰三角形
【答案】AC
【解析】对于A,因为 所以
即 ,所以 ,
结合 ,可得 或 (舍去),
所以 是等腰三角形,故A正确;
对于B,由正弦定理可得 ,则 ,
所以 为锐角,但无法判断 两角是否为锐角,故B错误;
对于C,因为 ,所以 ,即 ,
又因为 ,可得 ,即 是等边三角形,故C正确;
对于D,因为 ,所以 ,
所以 ,所以 或 ,即 或 ,
所以 是等腰三角形或直角三角形,故D错误.故选:AC.
【题型5 三角形的周长与面积】
满分技法
1、三角形面积公式的使用原则:对于面积公式S=absin C=acsin B=bcsin A,一般是使用哪一个角就使
用哪一个公式;
2、与面积有关的问题:一般要用到正弦定理和余弦定理进行边角互化;
3、三角形的周长问题:一般是利用余弦定理和公式a2+b2=(a+b)2-2ab将问题转化为求两边之和的问题.
17.(23-24高一下·云南昆明·月考)在 中,角A,B,C的对边分别是a,b,c,且三边满足
, ,则 的面积为( )
A. B. C. D.
【答案】A
【解析】因为 ,所以 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司又 ,由余弦定理得: ,
所以 ,
故 的面积 ,故选:A.
18.(23-24高一下·福建三明·期中)在 中,已知 , , ,则 的面积
为( )
A.4 B. C.2 D.1
【答案】B
【解析】由正弦定理得 ,
由余弦定理得 ,即 ,解得 ,
故 ,
所以 .故选:B
19.(23-24高一下·江苏南京·月考)已知 , , 分别是 的内角 , , 的对边,且
.
(1)求 ;
(2)若 , 的面积为 ,求 的周长.
【答案】(1) ;(2)10
【解析】(1)在 中, ,
由正弦定理得: ,则 ,
即 ,即 ,
由正弦定理得 ,即 ;
(2)由 ,得 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司则 ,得 ,
由余弦定理得 ,
即 ,整理得 ,
即 ,解得 ,则 ,
所以 的周长为 .
20.(23-24高一下·安徽·月考)在 中,角 , , 所对的边分别为 , , ,已知
(1)求 ;
(2)若 ,且 的周长为 ,求 的面积
【答案】(1) ;(2)
【解析】(1)由 ,得
得 ,得
由余弦定理得
由正弦定理得
所以 ,所以
因为 ,所以 .
(2)因为 ,且 的周长为 ,所以
由余弦定理可得
所以 ,解得 ,
因此 .
【题型6 三角形的外接圆问题】
满分技法
学科网(北京)股份有限公司 学科网(北京)股份有限公司利用正弦定理: 可求解三角形外接圆的半径.
若要求三角形外接圆半径的范围,一般将 用含角的式子表示,再通过三角函数的范围来求半径的范围.
21.(23-24高一下·宁夏石嘴山·期中)在 中,已知 , , ,则 的外接圆的直
径为( )
A. B. C. D.
【答案】C
【解析】由余弦定理得 ,
所以三角形外接圆直径为 .故选:C.
22.(23-24高一下·福建莆田·期中)在 中,角A、B、C所对的边分别为a、b、c,且
,若 ,则 外接圆半径为 .
【答案】
【解析】由 及正弦定理得 ,
即 ,即 ,由 ,则 ,所以 ,
因为 ,所以 ,所以 ,
所以由正弦定理得, 的外接圆半径为 .
23.(22-23高一下·湖北黄冈·期末)在 中,角A,B,C所对的边分别为a,b,c,
若 ,点D在边AB上, ,则 的外接圆的面积是
( )
A. B. C. D.
【答案】B
【解析】因为 ,所以由正弦定理得 ,
所以 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以 ,所以 ,
所以 ,因为 ,所以 ,
因为 ,所以 ,所以 ,
在 中,由正弦定理得 , ,所以 ,
因为 ,
所以 ,得 ,所以
在 中,由余弦定理得 ,
,所以 ,
设 外接圆半径为 ,
则由正弦定理得 ,所以 ,
所以 的外接圆的面积是 ,故选:B
24.(23-24高一下·福建宁德·期中)现给出两个条件:① ,②
,从中选出一个条件补充在下面的问题中,并以此为依据求解问题.(选
出一种可行的条件解答,若两个都选则按第一个解答计分)
在 中, , , 分别为内角A, , 所对的边,若________.
(1)求 ;
(2)若 的面积为 ,求 外接圆半径的最小值.
【答案】(1) ;(2)
【解析】(1)若选①:因为 ,
由正弦定理可得 ,
由 ,则 , ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司可得 ,所以得 ;
若选②:因为 ,即 ,
由正弦定理可得 ,
由余弦定理可得 ,
因为 ,所以 .
(2)由题意可得: ,则 ,
由余弦定理可知 ,
当且仅当 时,等号成立,即 ,
所以外接圆半径最小值为 .
【题型7 三角形的中线问题】
满分技法
1、中线长定理:在 中, 是边 上的中线,则 .
2、中线向量化:由 (核心技巧)得 (结论).
3、邻角互补应用:
核心技巧:
在 中有: ;
在 中有: .
25.(23-24高一下·重庆·期中)已知 的内角 的对边分别为 ,若 则
边上的中线 的长为 .
【答案】7
【解析】在 中,由余弦定理得 ,
因为 为 边上的中线,所以 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以 ,
所以 ,即 的长为7.
26.(23-24高一下·江苏南通·期中)如图,在 中,已知 分别为
边上的中点, 相交于点 .
(1)求 ;
(2)求 的值.
【答案】(1) ;(2) .
【解析】(1)因为 ,由余弦定理知:
,
所以 .
(2)设 ,
因为 分别为 的中点,
所以 .
因为 ,
所以 ,
.
又 ,.
所以 .
27.(23-24高二下·广西柳州·期中)在 中,角A,B,C所对的边分别为a,b,c,且
学科网(北京)股份有限公司 学科网(北京)股份有限公司.
(1)证明: 为等腰三角形.
(2)若D是边BC的中点, ,求 的面积.
【答案】(1)证明见解析;(2)
【解析】(1)证明:因为 由正弦定理得
因为 ,由余弦定理得 ,
代入 化简可得
所以 为等腰三角形。
(2)由题可知 因为D是边BC的中点, ,
在 和 中,利用余弦定理的推论得
代入 , 可得
由 得
则 的面积
28.(2024·浙江·模拟预测)在 中,角 所对的边分别为 , .
(1)求 的值;
(2)若 ,点 是 的中点,且 ,求 的面积.
【答案】(1) ;(2) .
【解析】(1)
由正弦定理得: ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司,则 , ,
不等于0, .
(2) , ,所以 ,
联立 , ,
在 中,由余弦定理得: ①
在 中,由余弦定理得: ②
由① ②式得:
故 ,
.
【题型8 三角形的角平分线问题】
满分技法
如图,在 中, 平分 ,角 , , 所对的边分别为
(1)利用角度的倍数关系:
(2)内角平分线定理: 为 的内角 的平分线,则 .
说明:三角形内角平分线性质定理将分对边所成的线段比转化为对应的两边之比,再结合抓星结构,
就可以转化为向量了,一般的,涉及到三角形中“定比”类问题,运用向量知识解决起来都较为简捷。
1 A 1 A 1
(3)等面积法:因为S +S =S ,所以 c∙ADsin + b∙ADsin = bcsinA,
∆ABD ∆ACD ∆ABC 2 2 2 2 2
学科网(北京)股份有限公司 学科网(北京)股份有限公司A
A 2bccos
所以(b+c)AD=2bc cos ,整理的: 2 (角平分线长公式)
2 AD=
b+c
29.(23-24高一下·广东深圳·期中)在 中,内角 的对边分别是 ,且 ,
平分 交BC于 , , ,则 的面积为 .
【答案】 /
【解析】由 平分 ,知 ,结合 ,就有
.
而 ,故 ,所以 .
由余弦定理得 ,
所以 ,
这得到 ,解得 (负值舍去),
所以 .
30.(23-24高一下·山东青岛·期中)在 中,角A、B、C的对边分别为a,b、c,若
, 是 的角平分线,点 在 上, , ,则
( )
A. B. C. D.4
【答案】A
【解析】因为 ,
所以由正弦定理可得 ,即 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司在 中, ,所以 ,
所以 ,即 ,
因为 , ,所以 ,
因为 ,所以 ,
因为 是 的角平分线,所以 ,
在 中, ,①
在 中, ,②
因为 ,所以 ,
由①②可得, ,解得, ,
所以,由余弦定理可得, .故选:A
31.(23-24高一下·江苏连云港·期中)已知 满足 .
(1)求 ;
(2)若 为 的角平分线, , ,求 的周长.
【答案】(1) ;(2) .
【解析】(1)在 中,由正弦定理: ,
则 , , ,
因为 ,
所以 ,即 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司由余弦定理: ,
因为 ,所以 ;
(2)设 边 上的高为 ,
因为 为 的角平分线,所以 ,
所以 的面积: ,
的面积: ,
因此 ,又 , ,所以 ,
在 中,由余弦定理:
,所以 ,
而 , ,所以 ,
又因为 ,即 ,解得 ,
所以 的周长为: .
32.(23-24高一下·福建厦门·期中)记 的内角A,B,C的对边分别为a,b,c,已知
.
(1)求角 的大小;
(2)若 点在线段BC上,且AD平分 ,若 ,且 ,求 .
【答案】(1) ;(2)
【解析】(1)由正弦定理可得 ,
所以 ,即 ,
可得 ,
整理可得 ,
因为在 中, ,所以 ,
又 ,所以 ;
学科网(北京)股份有限公司 学科网(北京)股份有限公司(2)因为 ,AD平分 ,
所以 ,
由 得 ,
即 ,整理可得 ,①
因为 为角平分线,所以 ,
在 中由正弦定理可得 ,
在 中由正弦定理可得 ,
又 ,所以 ,
所以 ,②
由①②可得 ,
在 中,由余弦定理可得 ,
解得 .
【题型9 多三角形或四边形中解三角形】
满分技法
在面对几何图形时,关键是寻找相应的三角形,并在三角形中利用正、余弦定理,特别时涉及到公共边
时,要利用公共边来过渡,即利用公共边创造互补或互余关系列式,其本质是构建关于角的关系的方程.
33.(22-23高一下·山东东营·期末)在平面四边形 中,已知 , , ,
, ,则四边形 的面积是( )
A. B. C. D.
学科网(北京)股份有限公司 学科网(北京)股份有限公司【答案】B
【解析】因为 ,则 ,
在 中,由余弦定理可得
,①
在 中,由余弦定理可得
,②
由①②可得 ,即 ,故 ,
因此,四边形 的面积是
,故选:B.
34.(23-24高一下·四川·期中)在凸四边形 中,若 , , , ,
,则 .
【答案】
【解析】在凸四边形 中,若 , , , , ,
如图所示:
在 中,利用余弦定理 ,
所以 ;
由于 , ,满足 ,
所以 ,即 为直角三角形;
由于 ,
则 ,
所以 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司35.(23-24高一下·浙江·期中)已知四边形 内接于圆 ,且满足 , , ,
则圆 的半径为( )
A. B. C. D.
【答案】A
【解析】由题意可得 ,
在 中,由余弦定理得 ,
在 中,由余弦定理得 ,
两式相减得 ,
因为 ,所以 ,
所以 ,
在 中,由正弦定理得圆 的半径为 ,故选:A
36.(22-23高一下·河南平顶山·期末)如图所示,四边形 的外接圆为圆
.
(1)求 ;
(2)若 ,求 的长.
【答案】(1) ;(2)
【解析】(1)由 ,可得 .
设 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司在 中,由余弦定理得 ,即 ,
解得 (舍去)或 ,
由正弦定理得 .
(2) ,
由已知得 ,
设 .
在 中,由余弦定理得 ,
,即 ..
【题型10 角或三角值的最值范围】
满分技法
求解三角形的角度范围问题,常见解题思路为:
(1)对所给条件做出分析,根据条件特点选择合适定理表达所求角度,若已知边长值较多则考虑余弦定
理,已知角度大小则考虑正弦定理;
(2)根据角度的具体表达式结构特点,讨论有关变量的具体定义域;
(3)选择三角函数求值域或基本函数求值域方式,在所求定义域内求得对应值域,即可得到问题所求的
角度相关范围大小.
37.(23-24高一下·天津河西·期中)在锐角 中,内角 , , 所对的边分别为 , , ,且
, ,则 的取值范围是( )
A. B. C. D.
【答案】D
【解析】锐角 中, , ,
由正弦定理可得 ,所以 ,
又 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以 ,解得 ,
所以 ,所以 .故选:D.
38.(23-24高一下·四川成都·期中)在锐角 中,内角 , , 的对边分别为 , , ,且满足
.则 的取值范围为( )
A. B. C. D.
【答案】B
【解析】由 ,
整理得 ,所以 ,
又 ,则 ,故 ,
,
因为 为锐角三角形,
所以 ,即 ,所以 ,
即 ,
所以 的取值范围为 .故选:B
39.(23-24高一下·山东青岛·期中)在锐角 中,角 的对边分别为 , 的面积为 ,
若 ,则 的取值范围为( )
A. B. C. D.
【答案】C
学科网(北京)股份有限公司 学科网(北京)股份有限公司【解析】在 中, ,
由 得 ,
因为 ,所以 ,
由余弦定理得 ,则 ,故 ,
又由正弦定理得 ,
整理得 ,
因为 ,故 或 (舍去),得 ,
为锐角三角形,故 ,解得 ,故 ,
所以 的取值范围是 .故选:C.
40.(23-24高一下·安徽宿州·期中)给出以下三个件:① ,② ,
③ .请从这三个条件中任选一个将下面的题目补充完整,并求解.已知在锐角 中,
内角 的对边分别为 且______.
(1)求边长 ;
(2)若 的面积 ,求角 的最大值.
【答案】(1) ;(2)
【解析】(1)选①,由 及余弦定理,得 ,所以 .
选②,由 及余弦定理,得 ,
整理得 ,所以 .
选③,由 ,得 ,
整理得 ,即 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司因此 ,由正弦定理得 ,所以 .
(2)显然 ,当且仅当 时取等号,而 ,
于是 ,由 ,得 ,
而 ,则有 ,
,因此 ,
在锐角 中,由 ,得 ,于是 ,解得 ,
所以角 的最大值为 .
【题型11 边长或周长的最值范围】
满分技法
求解与边长有关的范围问题,正余弦定理的灵活运用是解题的关键步骤,常见的解答思路一般表现为:
(1)根据已知条件的特点,选择合适的定理并代人具体值,得到与问题所求的对应关系等式;
(2)根据关系等式以及三角形三边之和、内角和关系特点,得到具体关系等式或不等式;
(3)通过运算,求出问题所求边长对应具体取值范围.
41.(23-24高一下·黑龙江哈尔滨·期中)在锐角三角形ABC中, , ,则
周长的取值范围是( ).
A. B. C. D.
【答案】C
【解析】根据题意, ,
由三角形面积公式和余弦定理可得, ,
即 ,
整理得, ,即 ,
在锐角三角形ABC中, ,
因为根据正弦定理 ,所以 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司因为三角形周长为 ,
又因为 ,所以 ,
所以 ,
因为 ,即 ,所以 ,
即 , ,
所以 .故选:C.
42.(23-24高一下·黑龙江大庆·期中)在 中,角A,B,C的对边分别为a,b,c,S为 的面
积, ,且 ,则 的周长的取值范围是( )
A. B. C. D.
【答案】B
【解析】若 ,则由余弦定理得 ,
而由面积公式得 ,故 ,
则 ,则 ,则 ,
则有 ,而在 中,可得 ,
由二倍角公式得 ,故 , ,
由正弦定理得 ,则 ,
可得 ,
,而 ,则 ,
显然当 时, 最大,且此时 ,故 ,
而易知 ,综上 ,故选:B
43.(23-24高一下·重庆渝中·期中)在 中,内角 的对边分别为 的面积为S,已知
学科网(北京)股份有限公司 学科网(北京)股份有限公司,且 .
(1)求 ;
(2)求 的取值范围.
【答案】(1) ;(2) .
【解析】(1)因为 ,所以 ,
在 中,由余弦定理,得 ,
因为 ,所以 ,
所以 ,所以 ,因为 ,所以 .
(2)在 中,由正弦定理,得 ,
所以
因为 ,所以 ,所以 ,
所以 ,即 的取值范围为 .
44.(23-24高一下·安徽·月考)在锐角 中,内角A,B,C的对边分别为a,b,c,已知:
,
(1)求b和角B;
(2)求 的取值范围.
【答案】(1) , ;(2)
【解析】(1)由 得 ,即 ,
,即 ,
因为 ,所以 ,解得 ,
因为 ,所以 ,
由 得 ,即 ,解得 或 (舍),
故 , .
学科网(北京)股份有限公司 学科网(北京)股份有限公司(2)
,
因为 为锐角三角形,所以 ,即 ,解得 ,
所以 ,则 ,
解得 ,即 的取值范围为
【题型12 三角形面积的最值范围】
满分技法
针对三角形面积进行提问的取值范围问题,属于中等难度的一类解三角形问题、可在选择填空或解答题中
遇见其“身影”解答这类问题,主要思路在于借助公式将面积问题等价转化为函数求值域或基本不等式求
最值,进而对问题作出具体完整的解答,这些解题思路在解题过程中具体可表现为:
(1)对所求三角形大致形状做出分析,明确选择面积求解公式;
(2)运用正余弦定理,取得三角形边长、角度具体值,将其代人面积公式中得到具体表达式;
(3)根据表达式结构特点,运用函数求值域思路或基本不等式求临界值思路,得到具体的范围大小,即对
应问题所求的面积范围值.
45.(23-24高一下·江西·月考)在 中,内角 的对边分别为 ,且
,则 面积的最大值为( )
A. B. C. D.6
【答案】B
【解析】因为 ,由余弦定理可得 ,
则 ,则 ,
又 ,所以 ,则 的面积 ,
当且仅当 ,即 时,等号成立,
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以 面积的最大值为 .故选:B.
46.(23-24高一下·福建泉州·月考)在锐角 中, 、 、 分别是角 、 、 所对的边,已知
且 ,则锐角 面积的取值范围为( )
A. B. C. D.
【答案】C
【解析】 且 , ,
根据正弦定理得, ,
即 ,
整理得 ,
, , ,解得 , ,
,
, ,
的面积
为锐角三角形, , ,
, ,
, .故选:C.
47.(23-24高一下·浙江·期中)已知 的内角 所对的边分别为 且 与
垂直.
学科网(北京)股份有限公司 学科网(北京)股份有限公司(1)求 大小;
(2)若 边上的中线长为 ,求 的面积的最大值.
【答案】(1) ;(2) .
【解析】(1)因为 , 垂直,
所以 .
由正弦定理,得 ,因为 ,
所以 , ,所以 .
(2)设 边上的中线为 ,
在 中,由余弦定理得: ,
即 ①.
在 和 中, ,
所以 ,
即 , , ,
化简得 ,
代入①式得, ,
由基本不等式 ,
∴ ,当且仅当 取到“ ”;
所以 的面积最大值为 .
48.(23-24高一下·山西·月考)在 中,内角A,B,C的对边分别为a,b,c,且
.
(1)求角B的大小;
学科网(北京)股份有限公司 学科网(北京)股份有限公司(2)若 为锐角三角形,且 ,求 的面积的取值范围.
【答案】(1) ;(2)
【解析】(1)因为 ,
由正弦定理得 ,
所以
,
又 ,所以 ,所以 ,即 ,
所以 ,可得 ,
所以 或 ,
又 ,所以 .
(2)由正弦定理 ,可得 ,
所以 ,
所以 ,
又由 为锐角三角形,且 ,则 ,解得 ,
因为 在 上单调递增,所以 ,
所以 ,即 的面积的取值范围是 .
【题型13 解三角形在实际中的应用】
满分技法
正、余弦定理在解决实际问题中的应用,本质上还是正、余弦定理在解决几何图形(主要是三角形与四边
学科网(北京)股份有限公司 学科网(北京)股份有限公司形)问题中的应用,因此利用几何图形本身及实际问题中涉及到的术语(如方位角等)构建恰当的三角
形,在三角形中运用正弦定理或余弦定理即可.
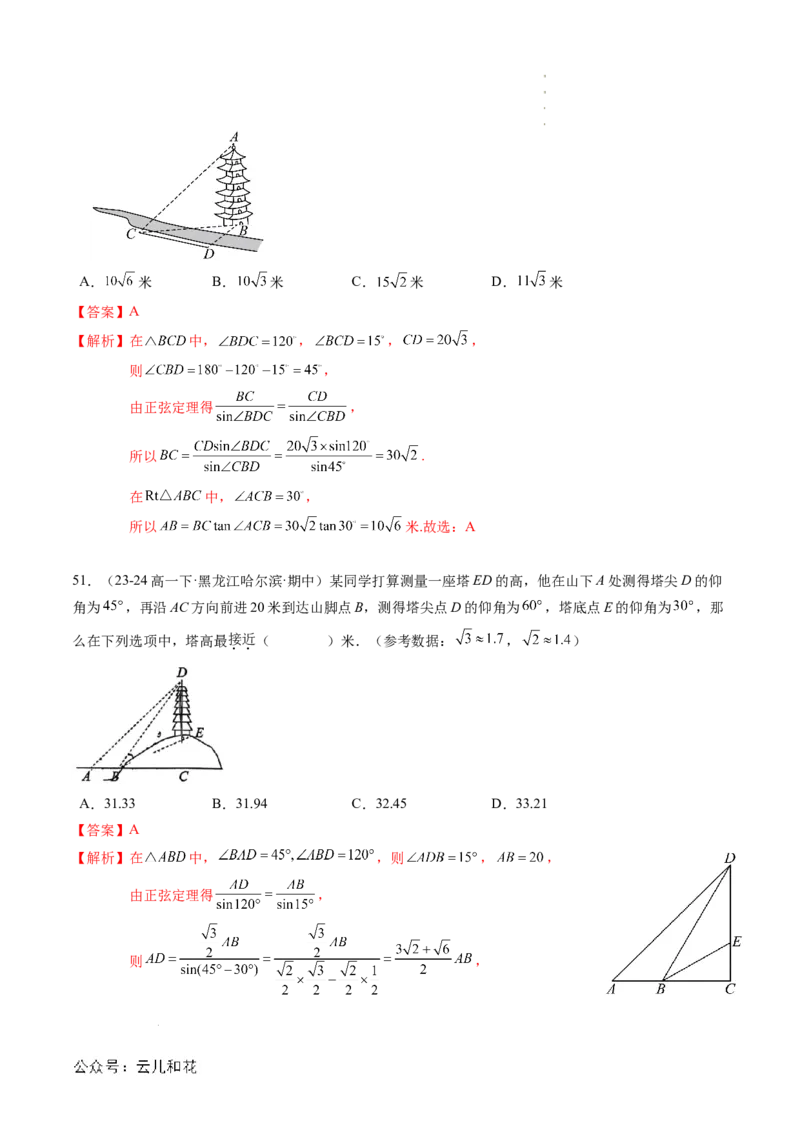
49.(23-24高一下·云南大理·期中)如图,为了测量两山顶 间的距离,飞机沿水平方向在 两点
进行测量, 在同一个铅垂平面内.已知飞机在 点时,测得 ,在 点时,
测得 , 千米,则 ( )
(提示: )
A. 千米 B. 千米 C. 千米 D. 千米
【答案】A
【解析】因为 ,可得 是等边三角形, 千米.
记直线 与直线 的交点为 ,
所以 为 的中点,所以 为等腰三角形,
,
又 ,
所以 千米,故选:A.
50.(23-24高一下·山东泰安·期中)如图,在测量河对岸的塔高 时,测量者选取了与塔底 在同一水
平面内的两个测量基点 与 ,并测得 , , 米,在点 处测得塔顶
的仰角为 ,则塔高 ( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. 米 B. 米 C. 米 D. 米
【答案】A
【解析】在 中, , , ,
则 ,
由正弦定理得 ,
所以 .
在 中, ,
所以 米.故选:A
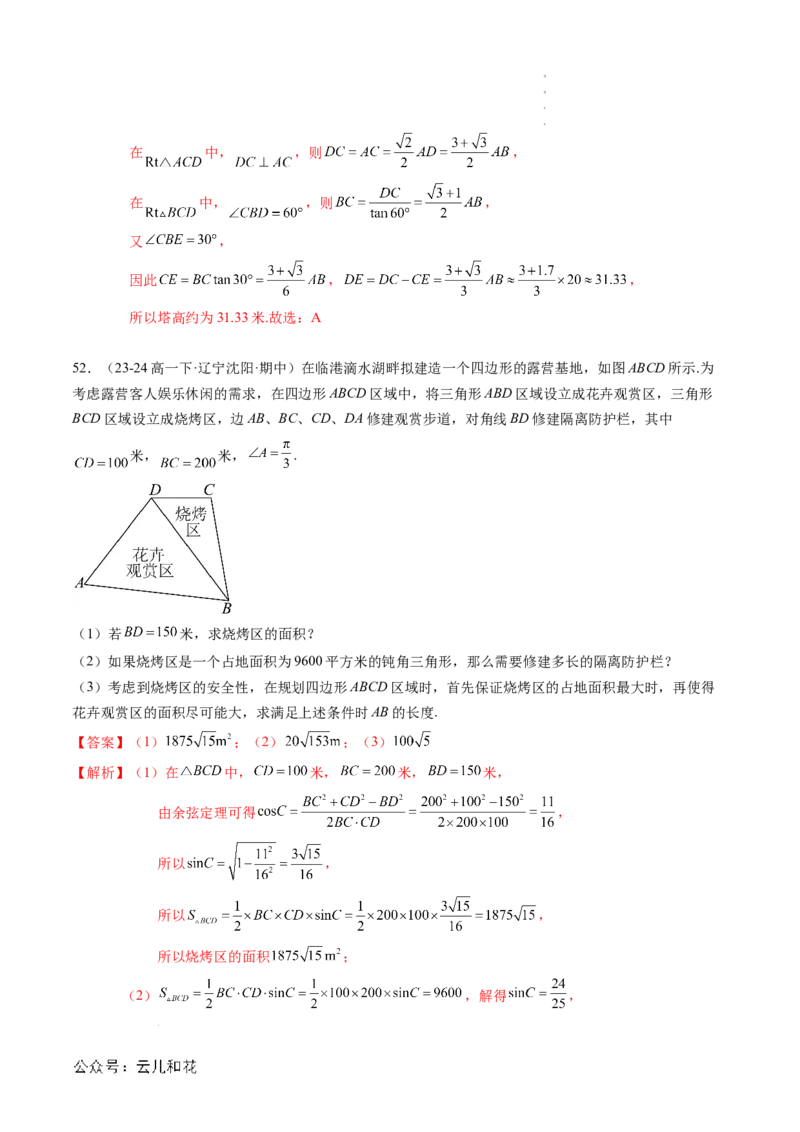
51.(23-24高一下·黑龙江哈尔滨·期中)某同学打算测量一座塔ED的高,他在山下A处测得塔尖D的仰
角为 ,再沿AC方向前进20米到达山脚点B,测得塔尖点D的仰角为 ,塔底点E的仰角为 ,那
么在下列选项中,塔高最接近( )米.(参考数据: , )
A.31.33 B.31.94 C.32.45 D.33.21
【答案】A
【解析】在 中, ,则 , ,
由正弦定理得 ,
则 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司在 中, ,则 ,
在 中, ,则 ,
又 ,
因此 , ,
所以塔高约为31.33米.故选:A
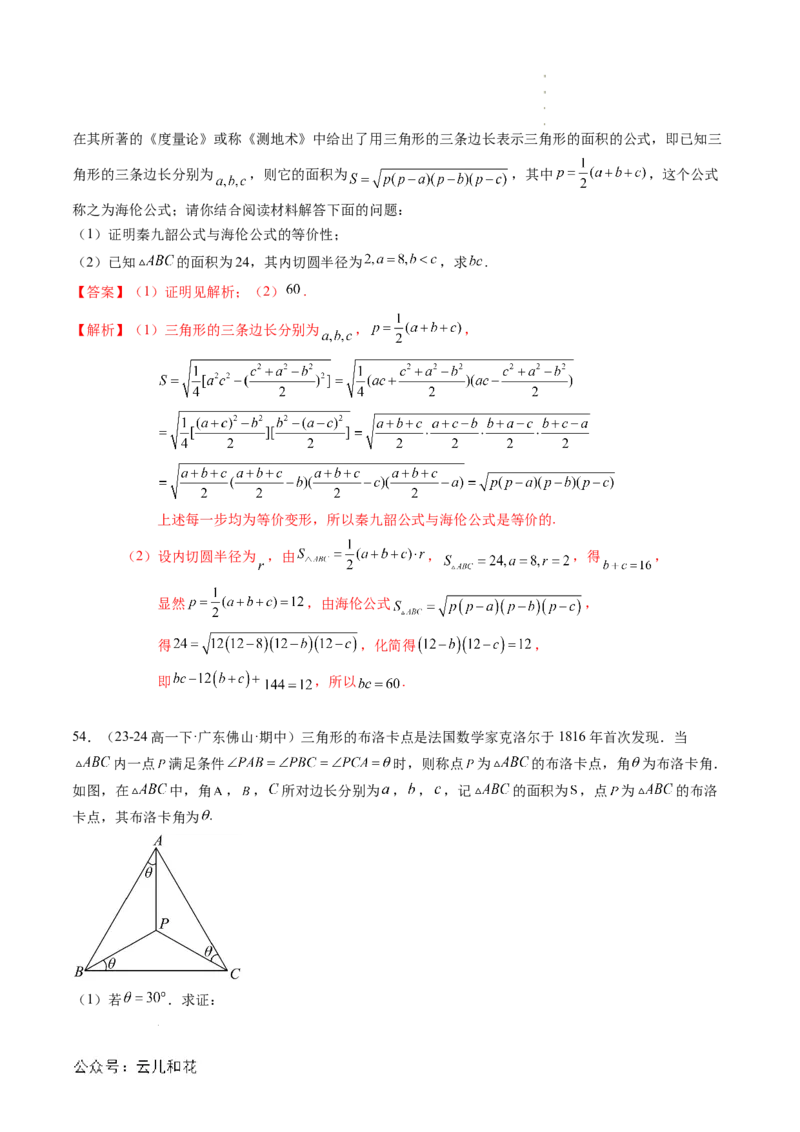
52.(23-24高一下·辽宁沈阳·期中)在临港滴水湖畔拟建造一个四边形的露营基地,如图ABCD所示.为
考虑露营客人娱乐休闲的需求,在四边形ABCD区域中,将三角形ABD区域设立成花卉观赏区,三角形
BCD区域设立成烧烤区,边AB、BC、CD、DA修建观赏步道,对角线BD修建隔离防护栏,其中
米, 米, .
(1)若 米,求烧烤区的面积?
(2)如果烧烤区是一个占地面积为9600平方米的钝角三角形,那么需要修建多长的隔离防护栏?
(3)考虑到烧烤区的安全性,在规划四边形ABCD区域时,首先保证烧烤区的占地面积最大时,再使得
花卉观赏区的面积尽可能大,求满足上述条件时AB的长度.
【答案】(1) ;(2) ;(3)
【解析】(1)在 中, 米, 米, 米,
由余弦定理可得 ,
所以 ,
所以 ,
所以烧烤区的面积 ;
(2) ,解得 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司因为C是钝角,所以 ,
故需要修建 的隔离防护栏;
(3) ,
当且仅当 时取到等号,此时 ,
设 ,
在 中, ,
,因为 ,则
当 ,即 时, ,
此时
【题型14 解三角形的新定义问题】
满分技法
解三角形的新定义问题通常涉及到对三角形的基本性质和定理的创新应用。解题时,首先需要理解新定义
的具体内容,包括它的定义、性质和应用场景。然后,根据新定义的特点,选择合适的数学工具和方法进
行解题。
53.(23-24高一下·广东河源·期中)阅读材料:材料一:我国南宋的数学家秦九韶在《数书九章》中提出
了“三斜求积术”:若把三角形的三条边分别称为小斜、中斜和大斜,记小斜为 ,中斜为 ,大斜为 ,
则三角形的面积为 .这个公式称之为秦九韶公式;材料二:古希腊数学家海伦
学科网(北京)股份有限公司 学科网(北京)股份有限公司在其所著的《度量论》或称《测地术》中给出了用三角形的三条边长表示三角形的面积的公式,即已知三
角形的三条边长分别为 ,则它的面积为 ,其中 ,这个公式
称之为海伦公式;请你结合阅读材料解答下面的问题:
(1)证明秦九韶公式与海伦公式的等价性;
(2)已知 的面积为24,其内切圆半径为 ,求 .
【答案】(1)证明见解析;(2) .
【解析】(1)三角形的三条边长分别为 , ,
上述每一步均为等价变形,所以秦九韶公式与海伦公式是等价的.
(2)设内切圆半径为 ,由 , ,得 ,
显然 ,由海伦公式 ,
得 ,化简得 ,
即 ,所以 .
54.(23-24高一下·广东佛山·期中)三角形的布洛卡点是法国数学家克洛尔于1816年首次发现.当
内一点 满足条件 时,则称点 为 的布洛卡点,角 为布洛卡角.
如图,在 中,角 , , 所对边长分别为 , , ,记 的面积为 ,点 为 的布洛
卡点,其布洛卡角为
(1)若 .求证:
学科网(北京)股份有限公司 学科网(北京)股份有限公司① ;
② 为等边三角形.
(2)若 求证: .
【答案】(1)①证明见解析,②证明见解析;(2)证明见解析
【解析】(1)①若 ,
则
,
所以 ,
在 中,分别由余弦定理得:
,
,
,
三式相加整理得 ,
即 ,所以 ;
②由余弦定理可得 ,
则
,
当且仅当 且 时取等号,
又 ,所以 ,所以 ,所以 ,
即当且仅当 且 时取等号,即当且仅当 为等边三角形时取等号,
所以 ,当且仅当 为等边三角形时取等号,
又由①知 ,所以 为等边三角形;
(2)由(1)得 ,
所以
,
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以 ,
又由余弦定理可得 ,
所以 ,
所以 ,所以 ,
由正弦定理可得 .
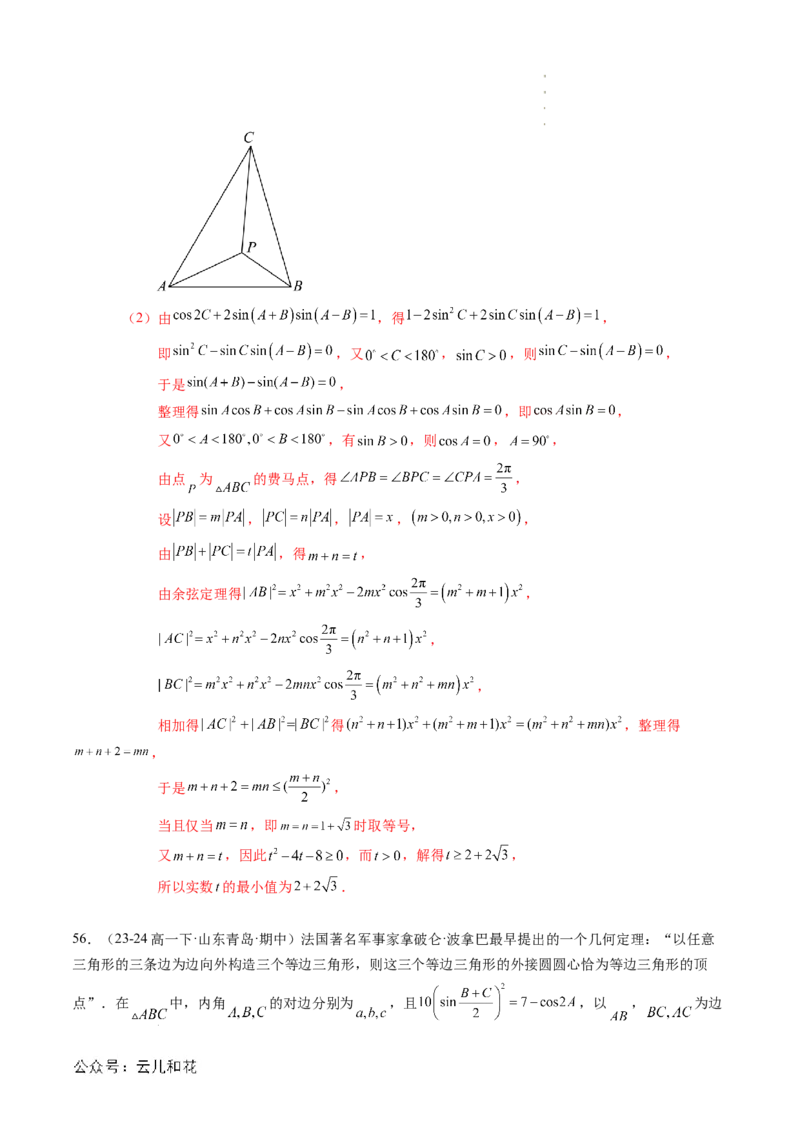
55.(23-24高一下·广东江门·月考)正等角中心(positive isogonal centre)亦称费马点,是三角形的巧合
点之一.“费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内
求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当
的三个内角均小于 时,使得 的点 即为费马点;当 有一个内角大
于或等于 时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知 的内角 所对
的边分别为 ,
(1)若 ,
①求 ;
②若 ,设点 为 的费马点,求 ;
(2)若 ,设点 为 的费马点, ,求实数 的最小
值.
【答案】(1)① ;② ;(2) .
【解析】(1)①在 中,由正弦定理及 ,得 ,
即 ,由余弦定理得 ,
又 ,所以 .
②由①知, ,则 的三个角都小于 ,
由费马点定义知: ,
设 ,由 得:
,整理得 ,
所以 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司(2)由 ,得 ,
即 ,又 , ,则 ,
于是 ,
整理得 ,即 ,
又 ,有 ,则 , ,
由点 为 的费马点,得 ,
设 , , , ,
由 ,得 ,
由余弦定理得 ,
,
,
相加得 得 ,整理得
,
于是 ,
当且仅当 ,即 时取等号,
又 ,因此 ,而 ,解得 ,
所以实数 的最小值为 .
56.(23-24高一下·山东青岛·期中)法国著名军事家拿破仑·波拿巴最早提出的一个几何定理:“以任意
三角形的三条边为边向外构造三个等边三角形,则这三个等边三角形的外接圆圆心恰为等边三角形的顶
点”.在 中,内角 的对边分别为 ,且 ,以 , 为边
学科网(北京)股份有限公司 学科网(北京)股份有限公司向外作三个等边三角形,其外接圆圆心依次为 .若 , 的面积为 ,求 的面
积.
【答案】
【解析】由 ,可得 ,
所以 ,可得 ,
解得 或 (舍去),
因为 ,所以 ,
如图所示,连接 ,由正弦定理得 ,
则 ,
在正 的面积为 ,所以 ,
又因为 ,可得 ,
在 中,由余弦定理得 ,
即 ,则 ,
在 中, ,且 ,由余弦定理 ,
可得 ,所以 ,
所以 的面积为 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司过关检测
一、单选题
1.(23-24高一下·江西宜春·期中)在 中,角 的对边分别为 ,若 ,则
( )
A. B. C. D.
【答案】A
【解析】因为 ,所以 ,
因为在 中, ,所以 .故选:A.
2.(23-24高一下·湖北武汉·月考)在 中,角 , , 的对边分别为 , , ,已知 ,
, ,则角 ( )
A. B. 或 C. D. 或
【答案】D
【解析】由正弦定理可得 ,即 ,解得 ,
因为 ,所以 ,
又 ,所以 或 ,
所以 或 .故选:D.
3.(23-24高一下·江苏连云港·期中)在三角形 中,若 ,则 是( )三角
形.
A.等腰 B.等腰 或Rt C.等腰直角 D.Rt
【答案】B
【解析】由正弦定理, 即 ,
因为 ,所以 或 ,
所以是等腰三角形或直角三角形.故选:B
学科网(北京)股份有限公司 学科网(北京)股份有限公司4.(23-24高一下·云南昆明·月考)在 中,角 所对的边分别为 ,已知 ,则
的外接圆面积为( )
A. B. C. D.
【答案】C
【解析】因为 ,所以由余弦定理可得 ,所以 ,
设 的外接圆半径为 ,由正弦定理可得 ,即 ,
则 的外接圆面积为 .故选:C
5.(23-24高一下·天津·期中)一个人骑自行车由A地出发向正东方向骑行了 到达 地,然后由 地
向南偏东 方向骑行了 到达 地,再从 地向北偏东 方向骑行了 到达 地,则 两地的距
离为( )
A. B. C. D.
【答案】A
【解析】由题可知, ,
所以 , ,所以 ,
在 中,由余弦定理得 ,
所以 ,
即 两地的距离为 .故选:A
6.(23-24高一下·江苏南通·期中)在 中,角 所对的边分别为 ,若 ,则
的取值范围是( )
A. B. C. D.
【答案】D
【解析】因为 ,则由正弦定理得 ,
又 ,
所以 ,
则 ,
又 , ,则
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以 或 ,即 或 (舍去),
则 ,
所以 ,解得 ,则 ,
所以
,
所以 的取值范围是 .故选:D.
二、多选题
7.(23-24高一下·广东广州·期中)在 中,角A,B,C的对边分别为a,b,c,则下列对 的个
数的判断正确的是( )
A.当 , , 时,有两解 B.当 , , 时,有一解
C.当 , , 时,有一解 D.当 , , 时,有两解
【答案】BC
【解析】对于A,由 , ,得 ,又 ,因此 唯一确定,A错误;
对于B, , , ,由余弦定理可得唯一 的值,B正确;
对于C,由 , ,得 ,则 ,有唯一角 的值,C正确;
对于D,由 , ,得 ,则 ,有唯一角 的值,D错误.故选:
BC
8.(23-24高一下·浙江丽水·期中)已知钝角 中,若 ,则下列命题中正确的是( )
A. B. C. D.
【答案】AC
【解析】对于A,由题意可知 ,且 ,则 ,
当 为锐角时,由 在 上单调递增,则 ,
当 为钝角时,即 ,则 ,所以 ,故A正确;
对于B,当 为钝角时,则 ,此时 ,故B错误;
学科网(北京)股份有限公司 学科网(北京)股份有限公司对于C,由题意可知 ,且函数 在 上单调递减,则 ,故C
正确;
对于D,当 , , 时, 符合题意,
则 , ,即 ,故D错误.故选:AC.
9.(23-24高一下·江苏南京·月考)在 中,角 , , 所对的边分别为 , , ,且
,则下列结论正确的是( )
A. B. 是钝角三角形
C.若 ,则 外接圆半径为 D.若 ,则边 上的中线长为
【答案】ABD
【解析】在 中,因为 ,
所以设 , , ,且 ,
对于A:由正弦定理,得 ,即选项A正确;
对于B:因为 ,所以角 最大,
则 ,
即 为钝角,即 是钝角三角形,即选项B正确;
对于C:若 ,
因为 ,所以 ,
由正弦定理,得 ,即 ,即选项C错误;
对于D:若 ,则 , ,
则由余弦定理得, ,
所以在 中,由余弦定理,边 上的中线长为:
,即选项D正确.故选:ABD.
三、填空题
10.(23-24高一下·上海·期中)已知 三边上的高分别为 、 、 ,且 ,则此三
学科网(北京)股份有限公司 学科网(北京)股份有限公司角形最大角的余弦值为 .
【答案】
【解析】因 的面积 ,则 ,故 ,
显然角 为最大角,不妨设 ( ),则 ,
由余弦定理, .
11.(23-24高一下·江苏镇江·月考)镇江西津渡的云台阁,是一座宋元风格的仿古建筑,始建于2010年,
目前已成为镇江市的地标建筑之一.如图,在云台阁旁水平地面上共线的三点A,B,C处测得其顶点P的
仰角分别为30°,60°,45°,且 米,则云台阁的高度为 米.
【答案】
【解析】设
在 中, , .
在 中, , ,
在 中, , .
在 中,由余弦定理得: ,
在 中,由余弦定理得: ,
因为 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以 , 即 , .
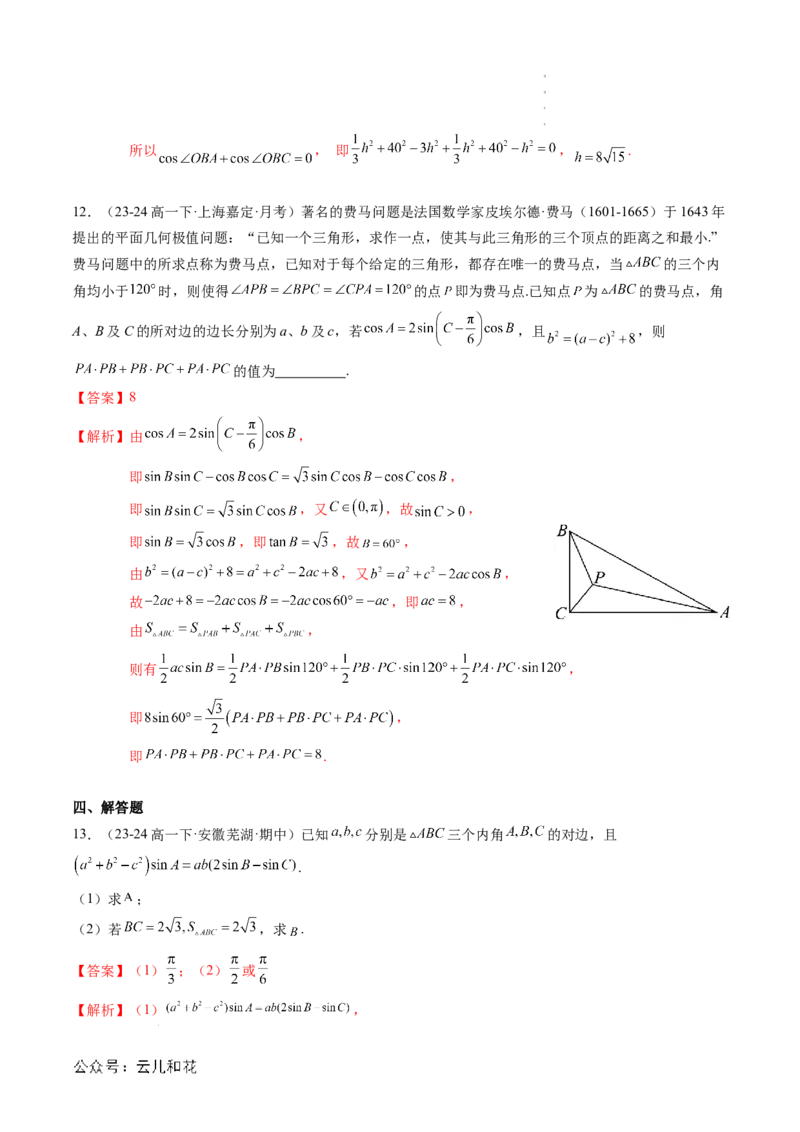
12.(23-24高一下·上海嘉定·月考)著名的费马问题是法国数学家皮埃尔德·费马(1601-1665)于1643年
提出的平面几何极值问题:“已知一个三角形,求作一点,使其与此三角形的三个顶点的距离之和最小.”
费马问题中的所求点称为费马点,已知对于每个给定的三角形,都存在唯一的费马点,当 的三个内
角均小于 时,则使得 的点 即为费马点.已知点 为 的费马点,角
A、B及C的所对边的边长分别为a、b及c,若 ,且 ,则
的值为 .
【答案】8
【解析】由 ,
即 ,
即 ,又 ,故 ,
即 ,即 ,故 ,
由 ,又 ,
故 ,即 ,
由 ,
则有 ,
即 ,
即 .
四、解答题
13.(23-24高一下·安徽芜湖·期中)已知 分别是 三个内角 的对边,且
.
(1)求 ;
(2)若 ,求 .
【答案】(1) ;(2) 或
【解析】(1) ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司由正弦定理得, ,
由 得, ,即 ,
所以 ,
又 ,得 ;
(2)由(1)知 , ,所以 ,
由余弦定理得, ,即 ,得 ,
所以 ,得 ,
当 时, ,此时 ,
所以 为直角三角形, ;
当 时, ,此时 ,
所以 为直角三角形, ,则 .
综上, 或 .
14.(23-24高一下·湖南·期中)设 的内角 的对边分别为 ,且 .
(1)求角 的大小;
(2)若 ,角 的平分线交 边于 ,求 的值.
【答案】(1) ;(2) .
【解析】(1)已知 ,由正弦定理得: ,
整理可得 ,所以 ,
由于 ,所以 .
(2)由 得 ,
角 的平分线交 边于 ,得 ,且 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司, ,
又 ,
联立 解得 或 ,
因为 ,
由角平分线定理可得, .
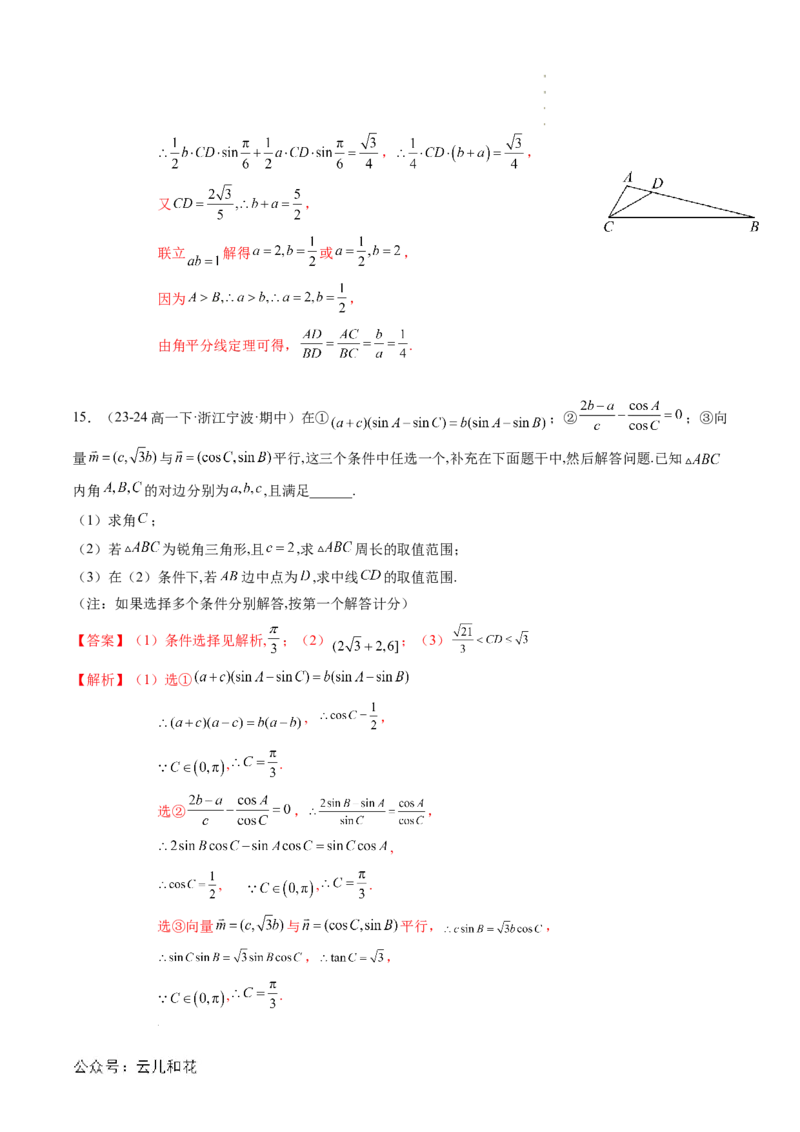
15.(23-24高一下·浙江宁波·期中)在① ;② ;③向
量 与 平行,这三个条件中任选一个,补充在下面题干中,然后解答问题.已知
内角 的对边分别为 ,且满足______.
(1)求角 ;
(2)若 为锐角三角形,且 ,求 周长的取值范围;
(3)在(2)条件下,若 边中点为 ,求中线 的取值范围.
(注:如果选择多个条件分别解答,按第一个解答计分)
【答案】(1)条件选择见解析, ;(2) ;(3)
【解析】(1)选①
, ,
, .
选② , ,
,
, , .
选③向量 与 平行, ,
, ,
, .
学科网(北京)股份有限公司 学科网(北京)股份有限公司(2) ,
,
.
为锐角三角形,
, .
周长的取值范围为 。
(3) ,
又由中线公式可得 ,
.
为锐角三角形,
, , .
学科网(北京)股份有限公司 学科网(北京)股份有限公司