文档内容
第一章 空间向量与立体几何全章综合测试卷(基础篇)
【人教A版(2019)】
考试时间:120分钟;满分:150分
姓名:___________班级:___________考号:___________
考卷信息:
本卷试题共22题,单选8题,多选4题,填空4题,解答6题,满分150分,限时120分钟,本卷题型针对性
较高,覆盖面广,选题有深度,可衡量学生掌握本章内容的具体情况!
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)(2023·江苏·高二专题练习)下列说法正确的是( )
A.任一空间向量与它的相反向量都不相等
B.不相等的两个空间向量的模必不相等
C.同平面向量一样,任意两个空间向量都不能比较大小
D.将空间向量所有的单位向量平移到同一起点,则它们的终点构成一个圆
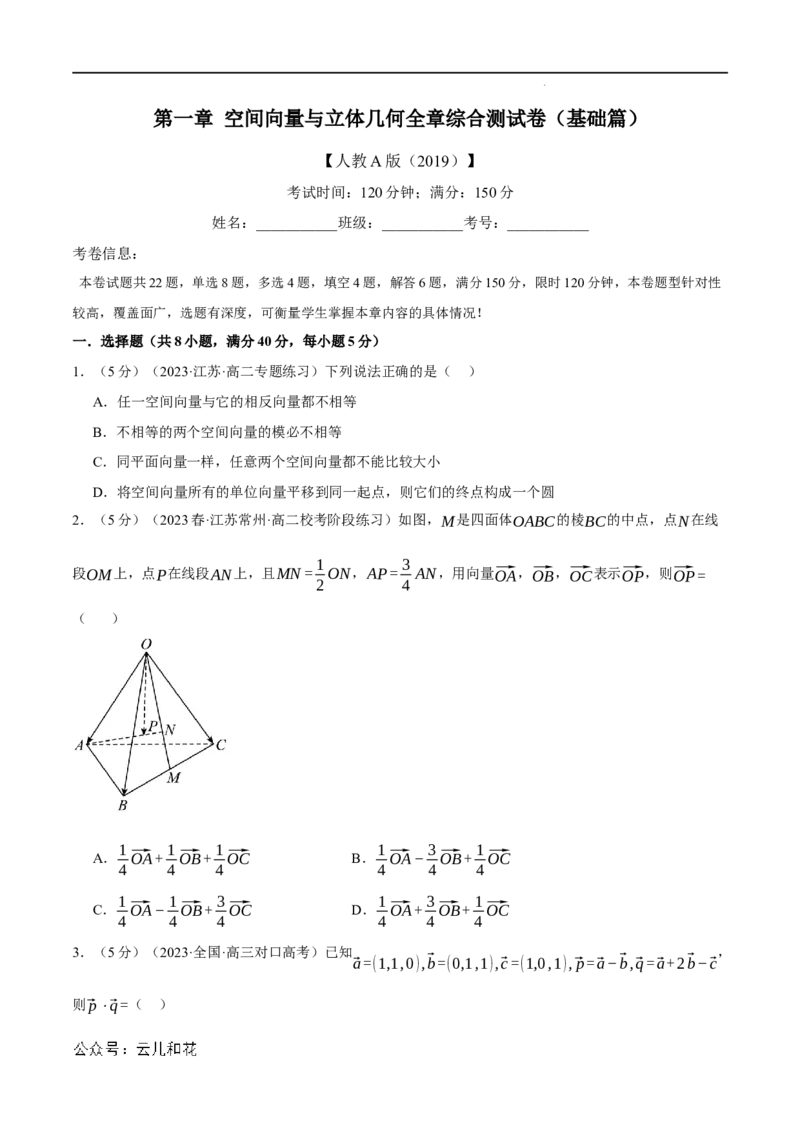
2.(5分)(2023春·江苏常州·高二校考阶段练习)如图,M是四面体OABC的棱BC的中点,点N在线
1 3
段OM上,点P在线段AN上,且MN= ON,AP= AN,用向量⃗OA,⃗OB,⃗OC表示⃗OP,则⃗OP=
2 4
( )
1 1 1 1 3 1
A. ⃗OA+ ⃗OB+ ⃗OC B. ⃗OA− ⃗OB+ ⃗OC
4 4 4 4 4 4
1 1 3 1 3 1
C. ⃗OA− ⃗OB+ ⃗OC D. ⃗OA+ ⃗OB+ ⃗OC
4 4 4 4 4 4
3.(5分)(2023·全国·高三对口高考)已知 ,
⃗a=(1,1,0),⃗b=(0,1,1),⃗c=(1,0,1),⃗p=⃗a−⃗b,⃗q=⃗a+2⃗b−⃗c
则⃗p⋅⃗q=( )
学科网(北京)股份有限公司A.−1 B.1 C.0 D.2
4.(5分)(2023秋·山西大同·高二校考期末)已知空间向量 ,且 ,则向量
⃗a=(1,0,1),⃗b=(x,1,2) ⃗a⋅⃗b=3
⃗a与⃗b的夹角为( )
5π 2π π π
A. B. C. D.
6 3 3 6
5.(5分)(2023秋·陕西宝鸡·高二统考期末)已知 ,则下
⃗a=(2,3,−1),⃗b=(2,0,−4),⃗c=(−4,−6,2)
列结论正确的是( )
A.⃗a⊥⃗b B.⃗a⊥⃗c C.⃗a//⃗b D.⃗a//⃗c
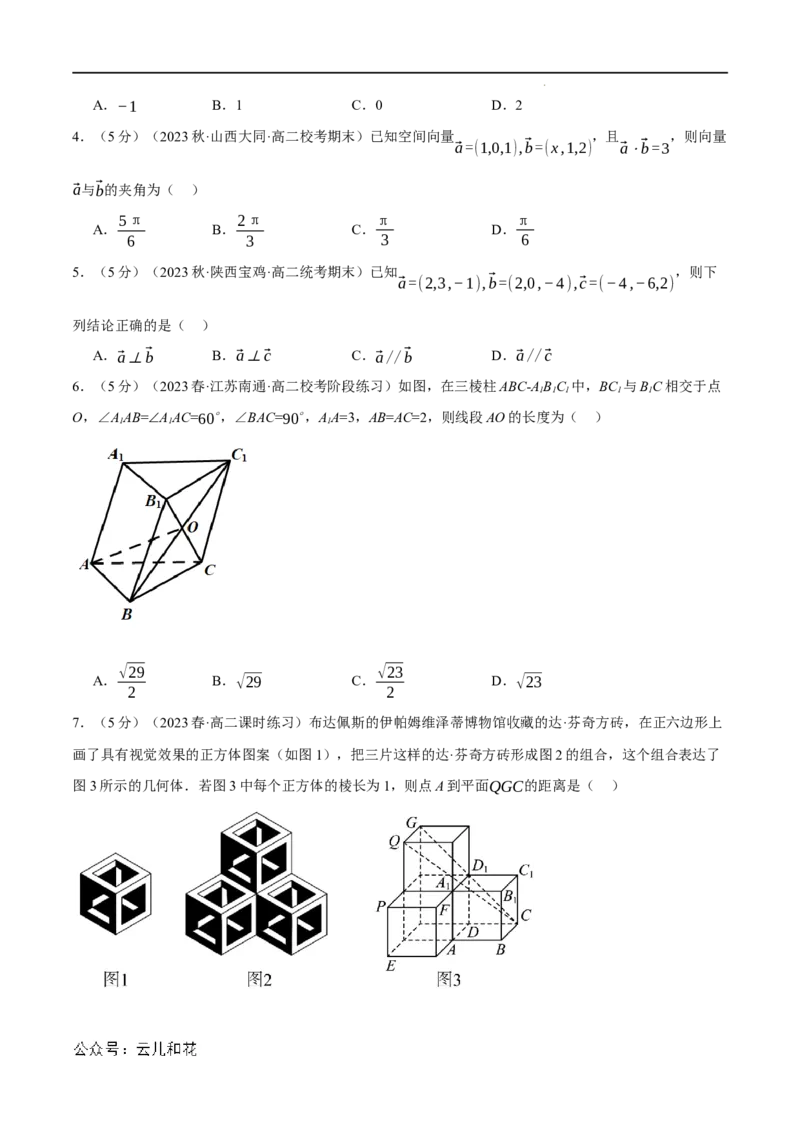
6.(5分)(2023春·江苏南通·高二校考阶段练习)如图,在三棱柱ABC-ABC 中,BC 与BC相交于点
1 1 1 1 1
O,∠AAB=∠AAC=60∘,∠BAC=90∘,AA=3,AB=AC=2,则线段AO的长度为( )
1 1 1
√29 √23
A. B.√29 C. D.√23
2 2
7.(5分)(2023春·高二课时练习)布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖,在正六边形上
画了具有视觉效果的正方体图案(如图1),把三片这样的达·芬奇方砖形成图2的组合,这个组合表达了
图3所示的几何体.若图3中每个正方体的棱长为1,则点A到平面QGC的距离是( )
学科网(北京)股份有限公司1 1 √2 √3
A. B. C. D.
4 2 2 2
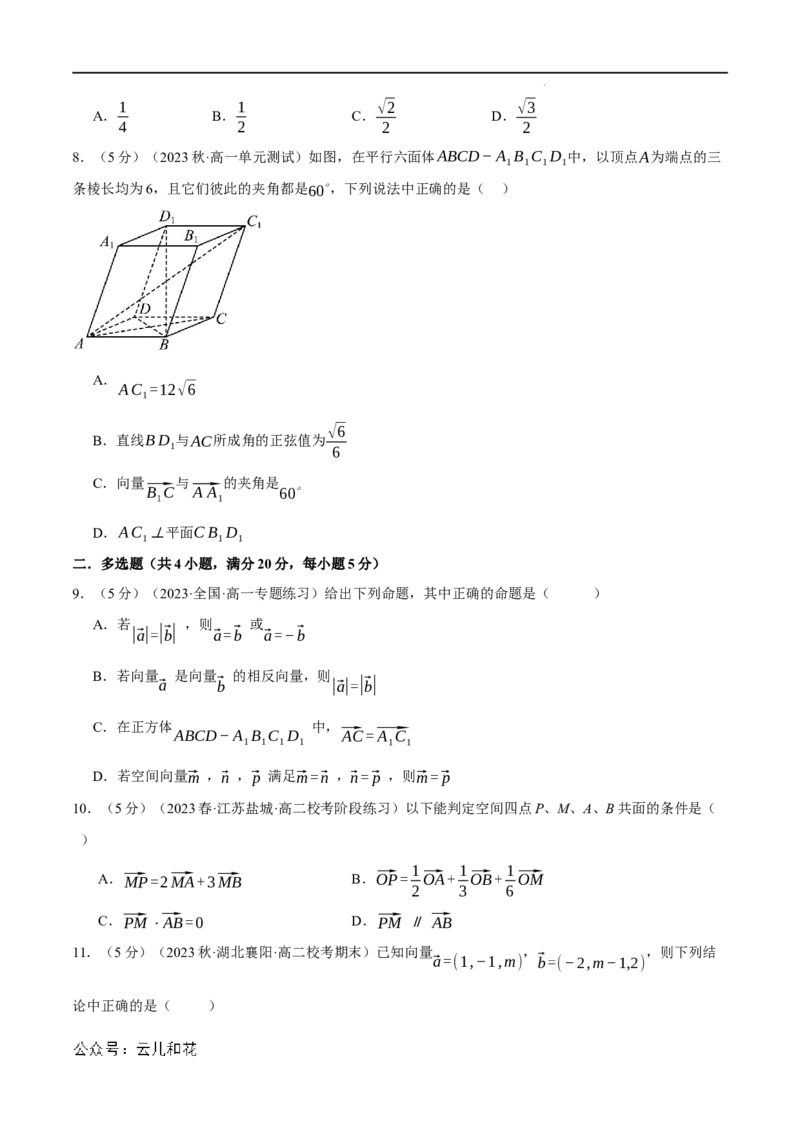
8.(5分)(2023秋·高一单元测试)如图,在平行六面体ABCD−A B C D 中,以顶点A为端点的三
1 1 1 1
条棱长均为6,且它们彼此的夹角都是60∘,下列说法中正确的是( )
A.
AC =12√6
1
√6
B.直线BD 与AC所成角的正弦值为
1 6
C.向量 与 的夹角是
⃗B C ⃗A A 60∘
1 1
D.AC ⊥平面CB D
1 1 1
二.多选题(共4小题,满分20分,每小题5分)
9.(5分)(2023·全国·高一专题练习)给出下列命题,其中正确的命题是( )
A.若 ,则 或
|⃗a|=|⃗b| ⃗a=⃗b ⃗a=−⃗b
B.若向量 是向量 的相反向量,则
⃗a ⃗b |⃗a|=|⃗b|
C.在正方体 中,
ABCD−A B C D ⃗AC=⃗A C
1 1 1 1 1 1
D.若空间向量⃗m ,⃗n ,⃗p 满足⃗m=⃗n ,⃗n=⃗p ,则⃗m=⃗p
10.(5分)(2023春·江苏盐城·高二校考阶段练习)以下能判定空间四点P、M、A、B共面的条件是(
)
1 1 1
A.⃗MP=2⃗MA+3⃗MB B.⃗OP= ⃗OA+ ⃗OB+ ⃗OM
2 3 6
C.⃗PM⋅⃗AB=0 D.⃗PM ∥ ⃗AB
11.(5分)(2023秋·湖北襄阳·高二校考期末)已知向量 , ,则下列结
⃗a=(1,−1,m) ⃗b=(−2,m−1,2)
论中正确的是( )
学科网(北京)股份有限公司A.若|⃗a|=2,则m=±√2
B.若⃗a⊥⃗b,则m=−1
C.不存在实数 ,使得⃗a=λ⃗b
D.若 ,则
⃗a⋅⃗b=−1 ⃗a+⃗b=(−1,−2,2)
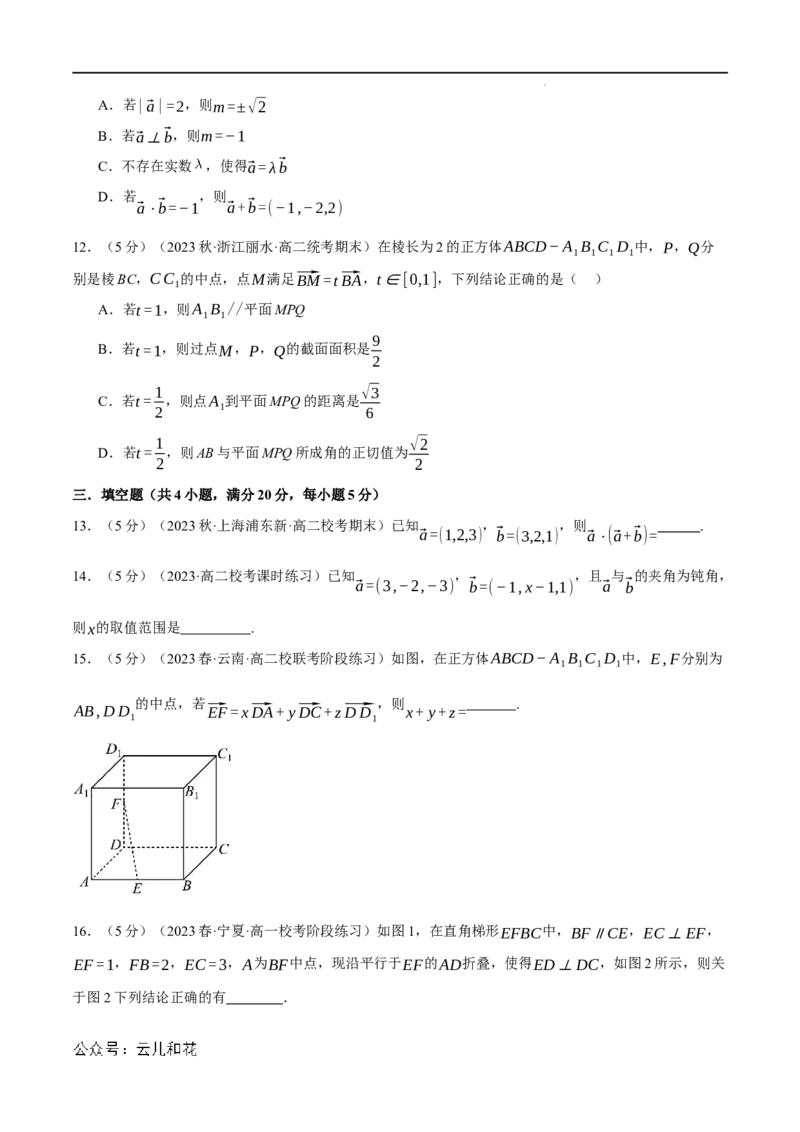
12.(5分)(2023秋·浙江丽水·高二统考期末)在棱长为2的正方体ABCD−A B C D 中,P,Q分
1 1 1 1
别是棱BC,CC 的中点,点M满足⃗BM=t⃗BA,t∈[0,1],下列结论正确的是( )
1
A.若t=1,则A B //平面MPQ
1 1
9
B.若t=1,则过点M,P,Q的截面面积是
2
1 √3
C.若t= ,则点A 到平面MPQ的距离是
2 1 6
1 √2
D.若t= ,则AB与平面MPQ所成角的正切值为
2 2
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)(2023秋·上海浦东新·高二校考期末)已知 , ,则 .
⃗a=(1,2,3) ⃗b=(3,2,1) ⃗a⋅(⃗a+⃗b)=
14.(5分)(2023·高二校考课时练习)已知 , ,且 与 的夹角为钝角,
⃗a=(3,−2,−3) ⃗b=(−1,x−1,1) ⃗a ⃗b
则x的取值范围是 .
15.(5分)(2023春·云南·高二校联考阶段练习)如图,在正方体ABCD−A B C D 中,E,F分别为
1 1 1 1
的中点,若 ,则 .
AB,DD ⃗EF=x⃗DA+ y⃗DC+z⃗DD x+ y+z=
1 1
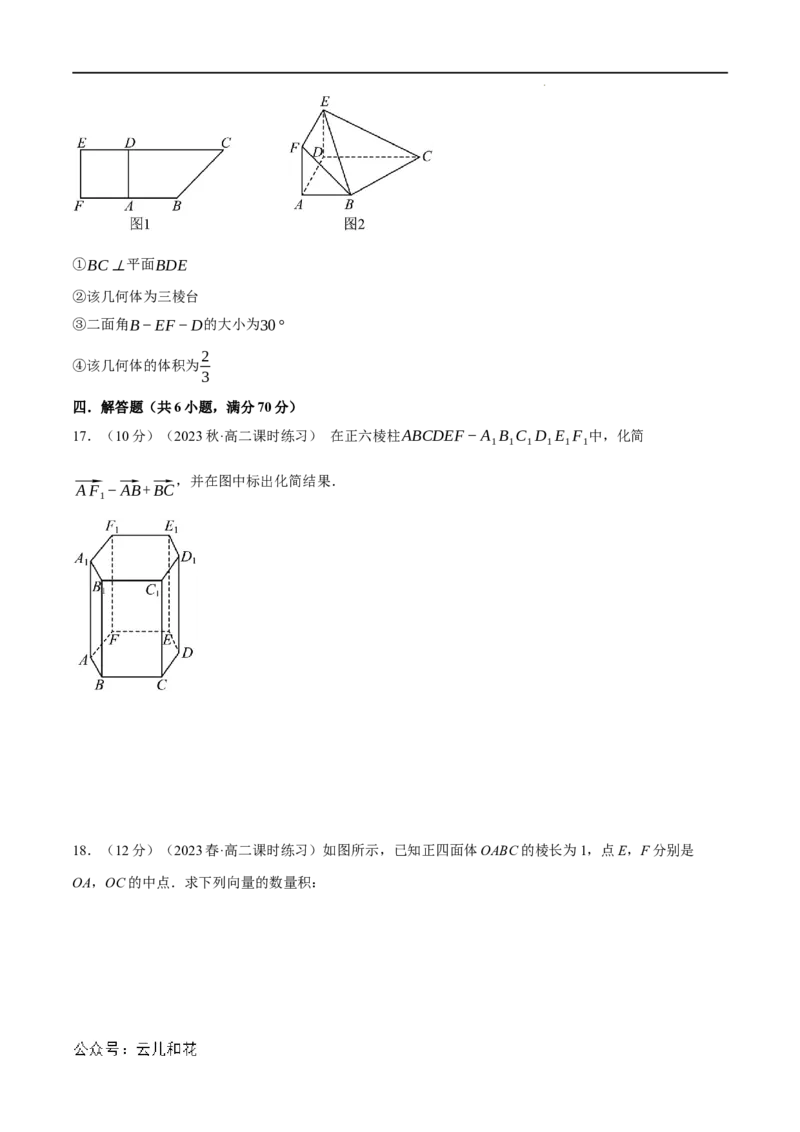
16.(5分)(2023春·宁夏·高一校考阶段练习)如图1,在直角梯形EFBC中,BF∥CE,EC⊥EF,
EF=1,FB=2,EC=3,A为BF中点,现沿平行于EF的AD折叠,使得ED⊥DC,如图2所示,则关
于图2下列结论正确的有 .
学科网(北京)股份有限公司①BC⊥平面BDE
②该几何体为三棱台
③二面角B−EF−D的大小为30°
2
④该几何体的体积为
3
四.解答题(共6小题,满分70分)
17.(10分)(2023秋·高二课时练习) 在正六棱柱ABCDEF−A B C D E F 中,化简
1 1 1 1 1 1
,并在图中标出化简结果.
⃗AF −⃗AB+⃗BC
1
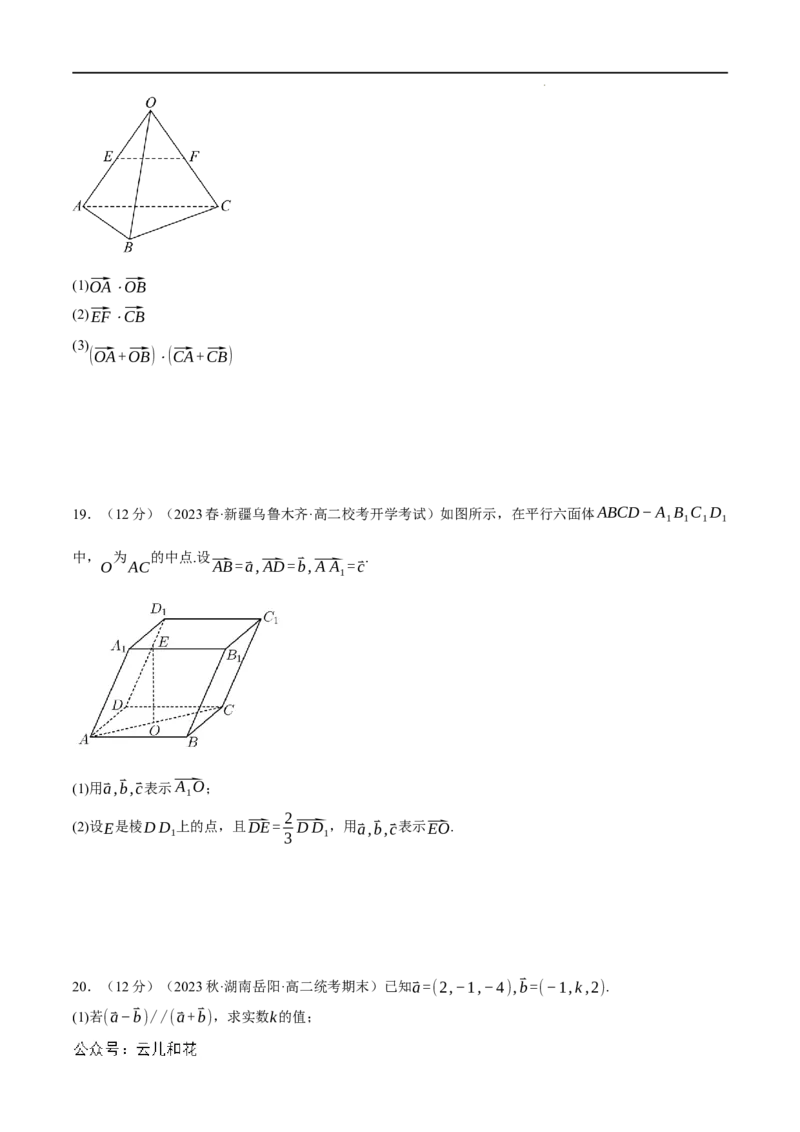
18.(12分)(2023春·高二课时练习)如图所示,已知正四面体OABC的棱长为1,点E,F分别是
OA,OC的中点.求下列向量的数量积:
学科网(北京)股份有限公司(1)⃗OA⋅⃗OB
(2)⃗EF⋅⃗CB
(3)
(⃗OA+⃗OB)⋅(⃗CA+⃗CB)
19.(12分)(2023春·新疆乌鲁木齐·高二校考开学考试)如图所示,在平行六面体ABCD−A B C D
1 1 1 1
中, 为 的中点.设 .
O AC ⃑AB=⃑a,⃑AD=⃑b,⃑A A =⃑c
1
(1)用⃑a,⃑b,⃑c表示⃑A O;
1
2
(2)设E是棱DD 上的点,且⃑DE= ⃑DD ,用 ⃑a,⃑b,⃑c表示⃑EO.
1 3 1
20.(12分)(2023秋·湖南岳阳·高二统考期末)已知⃑a=(2,−1,−4),⃑b=(−1,k,2).
(1)若(⃑a−⃑b)//(⃑a+⃑b),求实数k的值;
学科网(北京)股份有限公司(2)若(⃑a+3⃑b)⊥(⃑a+⃑b),求实数k的值.
21.(12分)(2023·全国·高三专题练习)如图,在四棱锥P−ABCD中,PA⊥底面ABCD,AD⊥AB,
AB//DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
(2)BE//平面PAD;
(3)平面PCD⊥平面PAD.
22.(12分)(2023·全国·高三专题练习)如图,在正方体ABCD−A B C D 中,E为BB 的中点.
1 1 1 1 1
(1)证明: 平面 ;
BC❑// AD E
1 1
(2)求直线BC 到平面AD E的距离;
1 1
(3)求平面AD E与平面ABCD夹角的余弦值.
1
学科网(北京)股份有限公司