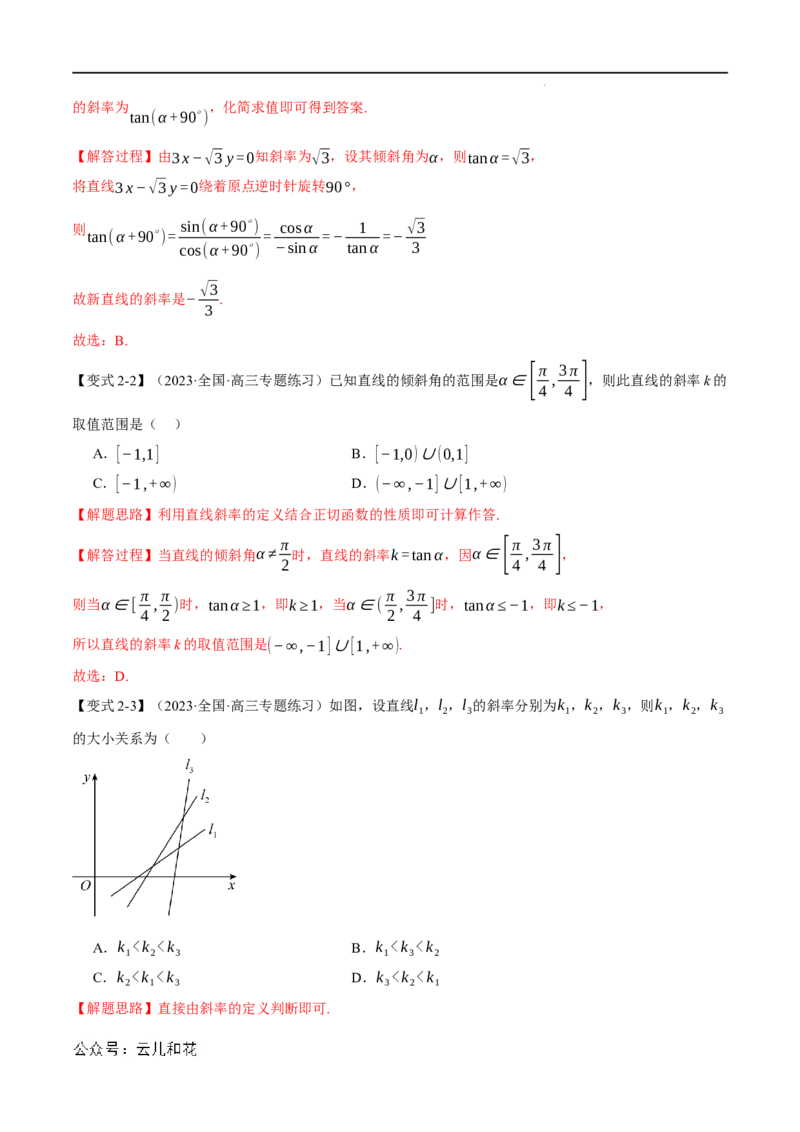文档内容
专题 2.1 直线的倾斜角与斜率【九大题型】
【人教A版(2019)】
【题型1 求直线的倾斜角】......................................................................................................................................2
【题型2 求直线的斜率】..........................................................................................................................................3
【题型3 已知直线的倾斜角或斜率求参数】.........................................................................................................5
【题型4 直线与线段的相交关系求斜率范围】.....................................................................................................6
【题型5 两条直线平行的判定】..............................................................................................................................9
【题型6 由两直线平行求参数】............................................................................................................................10
【题型7 两条直线垂直的判定】............................................................................................................................11
【题型8 由两直线垂直求参数】............................................................................................................................13
【题型9 直线平行、垂直的判定在几何中的应用】...........................................................................................14
【知识点1 直线的倾斜角与斜率】
1.直线的倾斜角
(1)倾斜角的定义
①当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l
的倾斜角.
②当直线l与x轴平行或重合时,规定它的倾斜角为0°.
(2)直线的倾斜角α的取值范围为 0° ≤ α <180° .
2.直线的斜率
(1)直线的斜率
把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k= tan α .
(2)斜率与倾斜角的对应关系
图示
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) k=0 k>0 不存在 k<0
(3)过两点的直线的斜率公式
过两点P(x,y),P(x,y)(x≠x)的直线的斜率公式为k=.
1 1 1 2 2 2 1 2
学科网(北京)股份有限公司【注】(1)倾斜角和斜率都可以表示直线的倾斜程度,二者相互联系.
(2)涉及直线与线段有交点问题,常根据数形结合思想,利用斜率公式求解.
【题型1 求直线的倾斜角】
【例1】(2023春·重庆沙坪坝·高一校考期末)直线x−√3 y+1=0的倾斜角是( )
A.30° B.60° C.120° D.150°
【解题思路】根据倾斜角与斜率之间的关系运算求解.
1 √3
【解答过程】因为x−√3 y+1=0的斜率k= = ,
√3 3
所以其倾斜角为30°.
故选:A.
【变式1-1】(2023春·山东青岛·高二统考开学考试)已知直线l的斜率为−1,则l的倾斜角为( )
A.30∘ B.45∘ C.60∘ D.135∘
【解题思路】根据斜率和倾斜角之间的关系即可得倾斜角.
【解答过程】解:因为斜率为-1,设直线倾斜角为α,0∘≤α<180∘,
所以tanα=−1,即α=135∘.
故选:D.
【变式1-2】(2023春·江苏南京·高二校考期中)直线l经过A(−1,0),B(1,2)两点,则直线l的倾斜角是
( )
π π 2π 3π
A. B. C. D.
6 4 3 4
【解题思路】设出直线的倾斜角α,求出其正切值,即斜率,进而可得出倾斜角.
2−0
【解答过程】设直线的倾斜角为α,由已知可得直线的斜率k=tanα= =1,
1+1
π
又α∈[0,π),所以倾斜角是 ,
4
故选:B.
【变式1-3】(2023·全国·高二专题练习)设直线l的斜率为k,且−1≤k<√3,直线l的倾斜角α的取值范
围为( )
A. [ 0, π ) ∪ (3π ,π ) B. [ 0, π ) ∪ (3π ,π )
3 4 6 4
C. ( π , 3π ) D. [ 0, π ) ∪ [3π ,π )
6 4 3 4
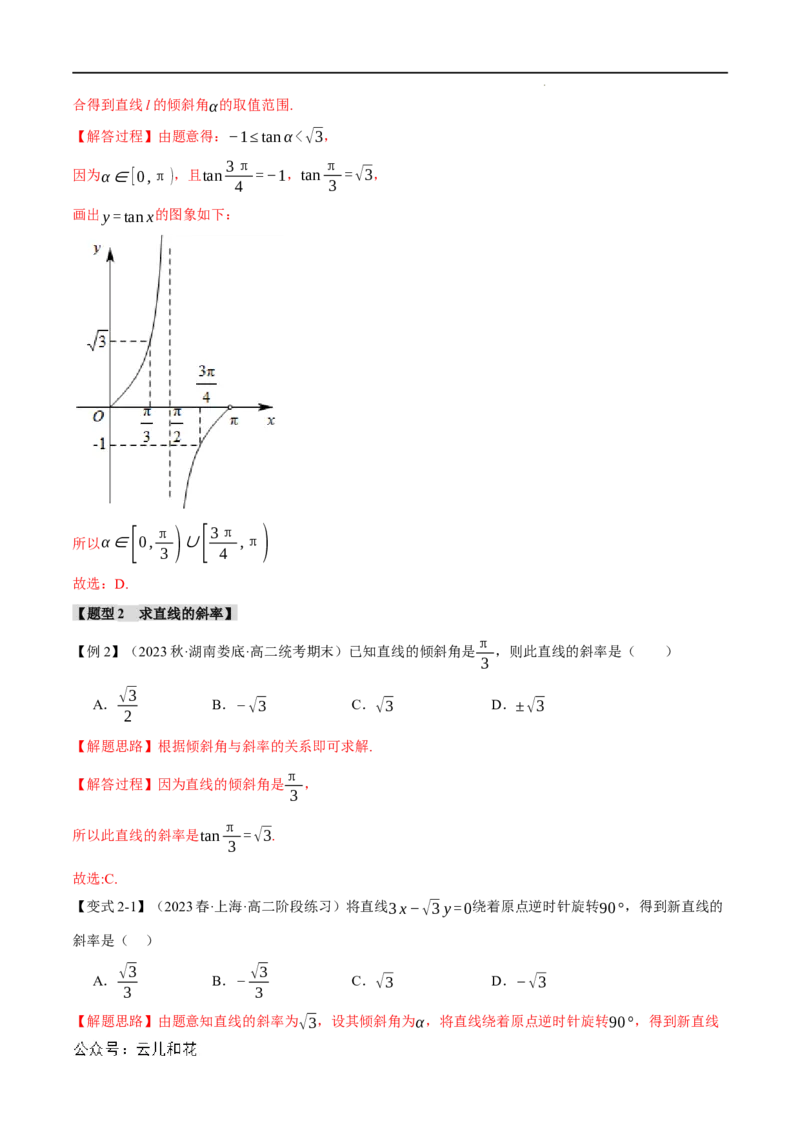
【解题思路】根据倾斜角与斜率的关系得到−1≤tanα<√3,结合正切函数的图象及α∈[0,π),数形结
学科网(北京)股份有限公司合得到直线l的倾斜角α的取值范围.
【解答过程】由题意得:−1≤tanα<√3,
3π π
因为α∈[0,π),且tan =−1,tan =√3,
4 3
画出y=tanx的图象如下:
所以α∈ [ 0, π ) ∪ [3π ,π )
3 4
故选:D.
【题型2 求直线的斜率】
π
【例2】(2023秋·湖南娄底·高二统考期末)已知直线的倾斜角是 ,则此直线的斜率是( )
3
√3
A. B.−√3 C.√3 D.±√3
2
【解题思路】根据倾斜角与斜率的关系即可求解.
π
【解答过程】因为直线的倾斜角是 ,
3
π
所以此直线的斜率是tan =√3.
3
故选:C.
【变式2-1】(2023春·上海·高二阶段练习)将直线3x−√3 y=0绕着原点逆时针旋转90°,得到新直线的
斜率是( )
√3 √3
A. B.− C.√3 D.−√3
3 3
【解题思路】由题意知直线的斜率为√3,设其倾斜角为α,将直线绕着原点逆时针旋转90°,得到新直线
学科网(北京)股份有限公司的斜率为 ,化简求值即可得到答案.
tan(α+90∘)
【解答过程】由3x−√3 y=0知斜率为√3,设其倾斜角为α,则tanα=√3,
将直线3x−√3 y=0绕着原点逆时针旋转90°,
则 sin(α+90∘) cosα 1 √3
tan(α+90∘)= = =− =−
cos(α+90∘) −sinα tanα 3
√3
故新直线的斜率是− .
3
故选:B.
[π 3π]
【变式2-2】(2023·全国·高三专题练习)已知直线的倾斜角的范围是α∈ , ,则此直线的斜率k的
4 4
取值范围是( )
A.[−1,1] B.[−1,0)∪(0,1]
C.[−1,+∞) D.(−∞,−1]∪[1,+∞)
【解题思路】利用直线斜率的定义结合正切函数的性质即可计算作答.
π [π 3π]
【解答过程】当直线的倾斜角α≠ 时,直线的斜率k=tanα,因α∈ , ,
2 4 4
π π π 3π
则当α∈[ , )时,tanα≥1,即k≥1,当α∈( , ]时,tanα≤−1,即k≤−1,
4 2 2 4
所以直线的斜率k的取值范围是(−∞,−1]∪[1,+∞).
故选:D.
【变式2-3】(2023·全国·高三专题练习)如图,设直线l ,l ,l 的斜率分别为k ,k ,k ,则k ,k ,k
1 2 3 1 2 3 1 2 3
的大小关系为( )
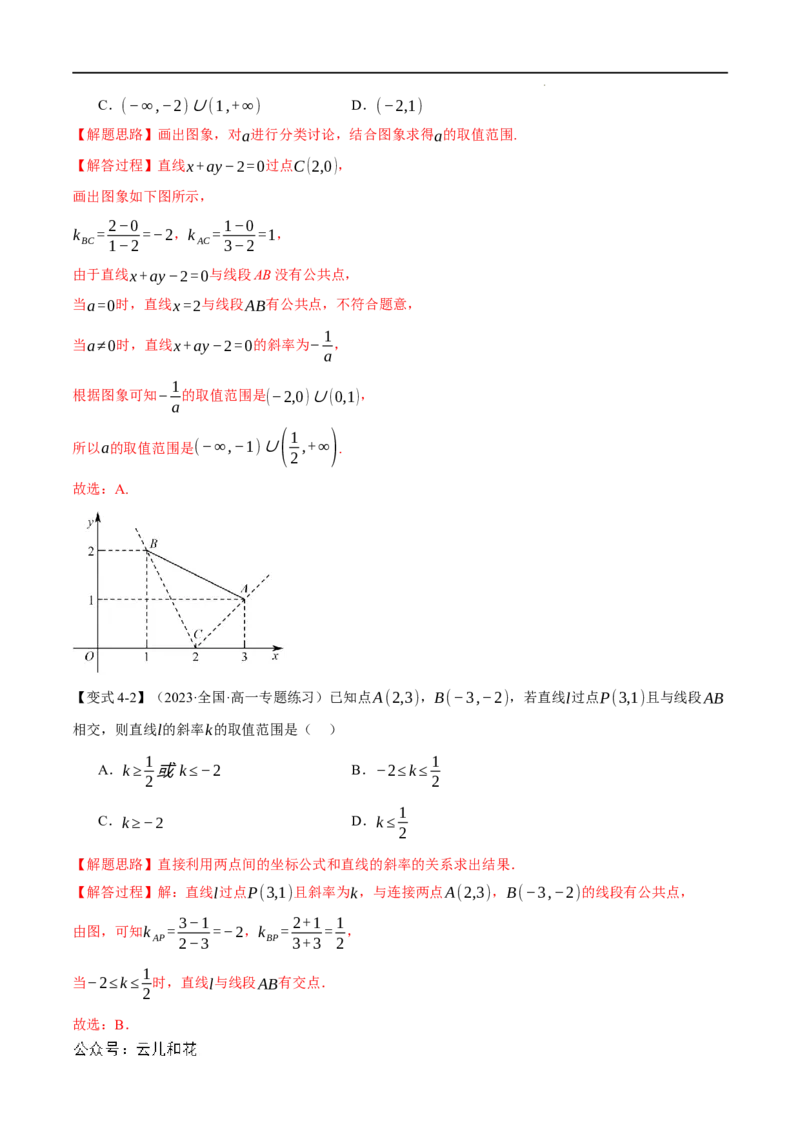
A.k 0 ,
m−2
解得20恒成立.
故方程有两相异实根,即l 与l 的斜率k,k 均存在.设两根为x,x,则kk=xx=-1,所以l⊥l.
1 2 1 2 1 2 1 2 1 2 1 2
故选:B.
2 ( 1)
【变式7-2】(2023春·安徽合肥·高二校考开学考试)若直线l 的斜率为− ,l 经过点A(1,1),B 0,− ,
1 3 2 2
则直线l 和l 的位置关系是( )
1 2
A.平行 B.垂直 C.相交不垂直 D.重合
【解题思路】根据直线斜率公式,结合两直线位置关系与斜率的关系进行判断即可.
( 1)
【解答过程】因为直线l 经过点A(1,1),B 0,− ,
2 2
1
− −1
所以直线l 的斜率为: 2 3,
2 =
0−1 2
3 2
又因为 ×(− )=−1,
2 3
所以两直线垂直,
故选:B.
【变式7-3】(2023春·上海杨浦·高二校考期中)下列各组直线中,互相垂直的一组是( )
A.2x−3 y−5=0与4x−6 y−5=0 B.2x−3 y−5=0与4x+6 y−5=0
C.2x−3 y−5=0与3x−2y−5=0 D.2x−3 y−5=0与6x+4 y−5=0
学科网(北京)股份有限公司【解题思路】分别求出两直线的斜率,根据斜率之积为−1两直线垂直,即可判断.
2 2
【解答过程】对于A:直线2x−3 y−5=0的斜率为 ,直线4x−6 y−5=0的斜率为 ,
3 3
故两直线平行,故A错误;
2 2
对于B:直线2x−3 y−5=0的斜率为 ,直线4x+6 y−5=0的斜率为− ,
3 3
斜率之积不为−1,即两直线不垂直,故B错误;
2 3
对于C:直线2x−3 y−5=0的斜率为 ,直线3x−2y−5=0的斜率为 ,
3 2
斜率之积不为−1,即两直线不垂直,故C错误;
2 3
对于D:直线2x−3 y−5=0的斜率为 ,直线6x+4 y−5=0的斜率为− ,
3 2
斜率之积为−1,即两直线垂直,故D正确;
故选:D.
【题型8 由两直线垂直求参数】
【例8】(2023春·江西宜春·高二校考期末)若直线l :ax+3 y+2=0与直线l :x−(a+1)y+a=0垂直,
1 2
则实数a=( )
3 3
A.0 B.1 C.− D.−
4 2
【解题思路】根据已知条件,结合直线垂直的性质,即可求解.
【解答过程】直线l :ax+3 y+2=0与直线l :x−(a+1)y+a=0垂直,
1 2
3
则a−3(a+1)=0,解得a=− .
2
故选:D.
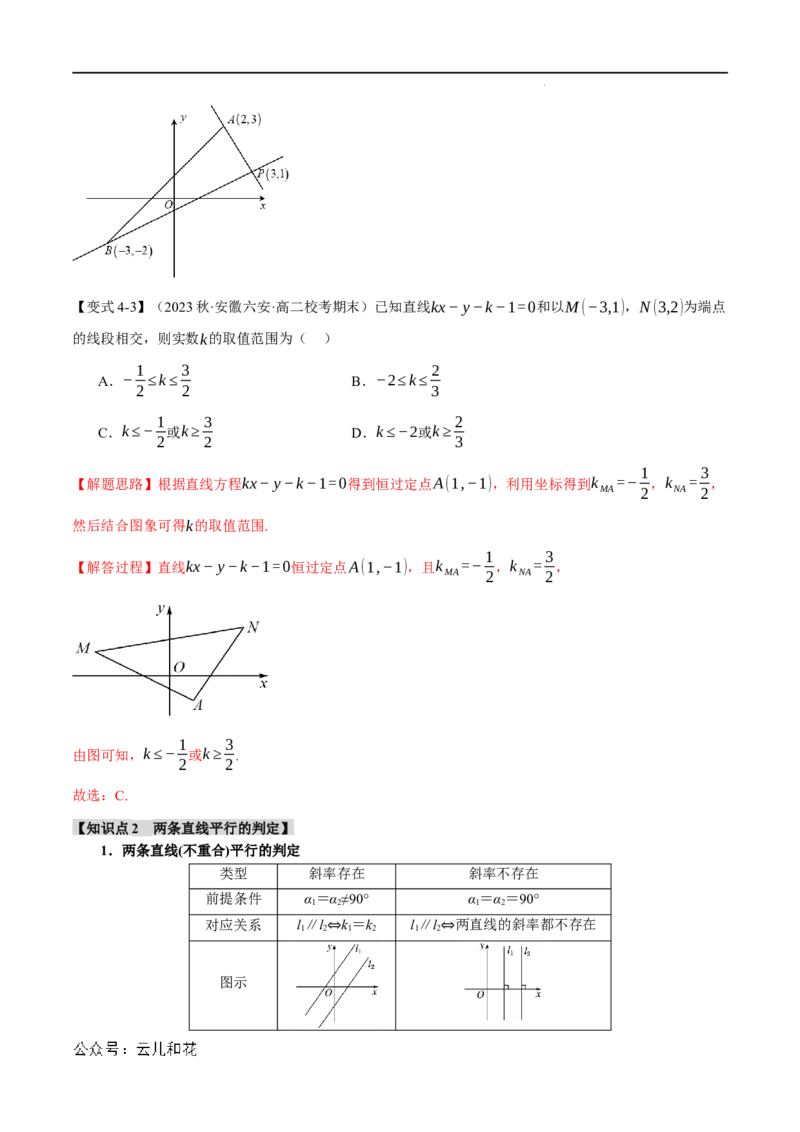
【变式8-1】(2023春·重庆沙坪坝·高一校考期末)直线 : ,则“
l (a2−a−2)x+(2a2−5a+2)y+a=0
1
a= ”是“直线l与x轴垂直”的( )
2
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解题思路】由直线l与x轴垂直,可得直线l的斜率不存在,进而得到¿,解出a的值,再根据充分条件和
必要条件的定义判断即可求解.
【解答过程】由直线l与x轴垂直,得直线l的斜率不存在,
学科网(北京)股份有限公司1
可得¿,解得a= ,
2
1
所以“a= ”是“直线l与x轴垂直”的充要条件.
2
故选:C.
【变式8-2】(2023春·甘肃兰州·高二校考开学考试)已知经过点A(−2,0)和点B(1,3a)的直线l 与经过点
1
P(0,−1)和点Q(a,−2a)的直线l 互相垂直,则实数a的值为( )
2
A.0 B.1 C.0或1 D.−1或1
【解题思路】求出直线l 的斜率为k =a,分a≠0、a=0两种情况讨论,在a≠0时,由两直线斜率之积为
1 1
−1可求得实数a的值;在a=0时,直接验证l ⊥l .综合可得结果.
1 2
3a−0
【解答过程】直线l 的斜率k = =a.
1 1 1−(−2)
−2a−(−1) 1−2a
①当a≠0时,直线l 的斜率k = = .
2 2 a−0 a
1−2a
因为l ⊥l ,所以k k =−1,即a⋅ =−1,解得a=1.
1 2 1 2 a
②当a=0时,P(0,−1)、Q(0,0),此时直线l 为y轴,
2
又A(−2,0)、B(1,0),则直线l 为x轴,显然l ⊥l .
1 1 2
综上可知,a=0或1.
故选:C.
【变式8-3】(2023·全国·高三专题练习)若直线ax−4 y+2=0与直线2x+5 y+c=0垂直,垂足为(1,b),
则a+b+c=( )
A.−6 B.4 C.−10 D.−4
【解题思路】根据垂直关系可求a,再根据点在直线上可求b,c,从而可得正确的选项.
【解答过程】因为ax−4 y+2=0与直线2x+5 y+c=0垂直,故2a−20=0即a=10,
10×1−4×b+2=0 b=3
因为垂足为(1,b),故{ ,故{ ,
2×1+5×b+c=0 c=−17
故a+b+c=−4,
故选:D.
【题型9 直线平行、垂直的判定在几何中的应用】
【例9】(2023春·山东滨州·高一校考阶段练习)已知点A(−4,3),B(2,5),C(6,3),D(−3,0),试判定
四边形ABCD的形状.
【解题思路】求出四边斜率,然后再判断形状.
学科网(北京)股份有限公司【解答过程】由斜率公式可得:
5−3 1
k = =
AB 2−(−4) 3
0−3 1
k = =
CD −3−6 3
0−3
k = =−3
AD −3−(−4)
3−5 1
k = =−
BC 6−2 2
k =k ,
AB CD
∴AB//CD
∵k ≠k
AD BC
∴AD与BC不平行
1
又∵k ⋅k = ×(−3)=−1,
AB AD 3
∴AB⊥AD,
故四边形ABCD是直角梯形.
【变式9-1】(2023秋·高二课时练习)已知△ABC的顶点分别为A(5,−1)、B(1,1)、C(2,m),若
△ABC为直角三角形,求实数m的值.
【解题思路】根据直角顶点分类讨论,由垂直关系列式求解
m+1 1+1
【解答过程】①若∠A为直角,则AC⊥AB,所以k ⋅k =−1,即 × =−1,解得m=−7;
AC AB 2−5 1−5
1+1 m−1
②若∠B为直角,则AB⊥BC,所以k ⋅k =−1,即 × =−1,
AB BC 1−5 2−1
解得m=3;
m+1 m−1
③若∠C为直角,则AC⊥BC,所以k ⋅k =−1,即 × =−1,
AC BC 2−5 2−1
解得m=±2.
综上,m的值为−7,−2,2或3.
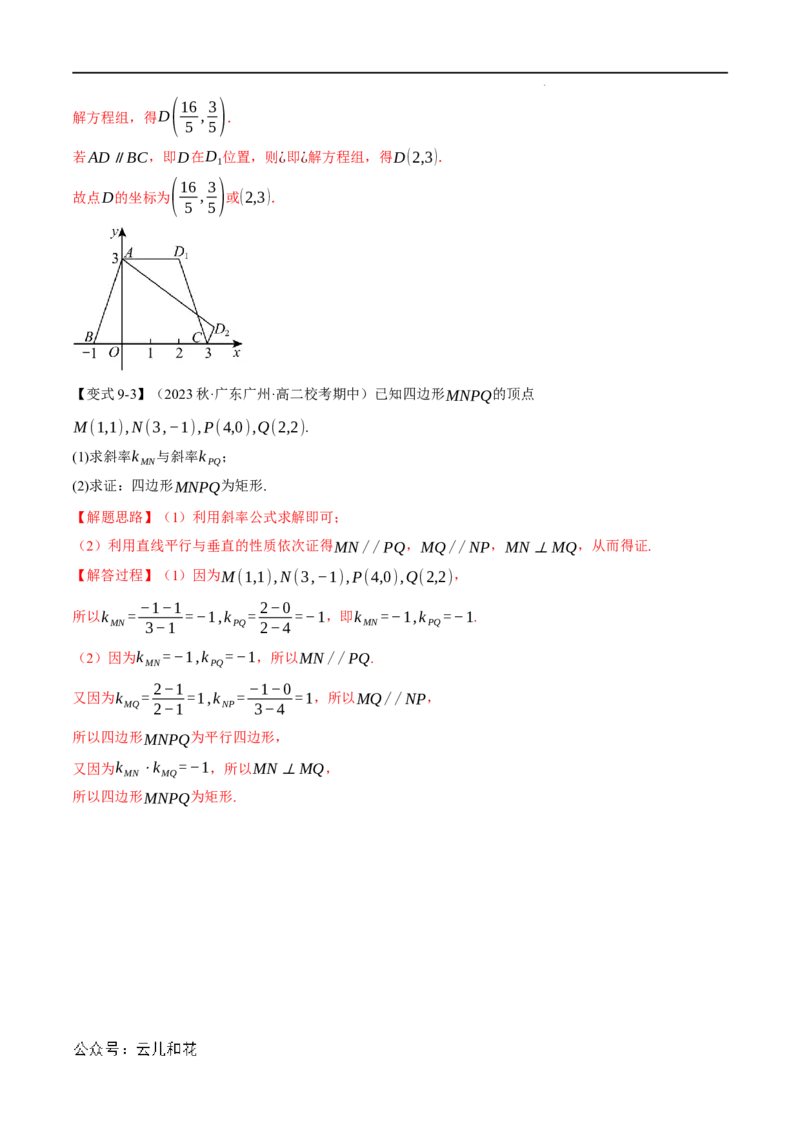
【变式9-2】(2023·全国·高三对口高考)已知A(0,3),B(−1,0),C(3,0),求点D的坐标,使四边形
ABCD为等腰梯形.
【解题思路】根据D的位置分类讨论,再根据等腰与两底平行列方程组解得结果.
【解答过程】设D(x,y).
若AB∥CD,即D在D 位置,则¿
2
即¿
学科网(北京)股份有限公司(16 3)
解方程组,得D , .
5 5
若AD∥BC,即D在D 位置,则¿即¿解方程组,得D(2,3).
1
(16 3)
故点D的坐标为 , 或(2,3).
5 5
【变式9-3】(2023秋·广东广州·高二校考期中)已知四边形MNPQ的顶点
M(1,1),N(3,−1),P(4,0),Q(2,2).
(1)求斜率k 与斜率k ;
MN PQ
(2)求证:四边形MNPQ为矩形.
【解题思路】(1)利用斜率公式求解即可;
(2)利用直线平行与垂直的性质依次证得MN//PQ,MQ//NP,MN⊥MQ,从而得证.
【解答过程】(1)因为M(1,1),N(3,−1),P(4,0),Q(2,2),
−1−1 2−0
所以k = =−1,k = =−1,即k =−1,k =−1.
MN 3−1 PQ 2−4 MN PQ
(2)因为k =−1,k =−1,所以MN//PQ.
MN PQ
2−1 −1−0
又因为k = =1,k = =1,所以MQ//NP,
MQ 2−1 NP 3−4
所以四边形MNPQ为平行四边形,
又因为k ⋅k =−1,所以MN⊥MQ,
MN MQ
所以四边形MNPQ为矩形.
学科网(北京)股份有限公司