23.11月金华高三十校联考物理答案(1)_2023年11月_0211月合集_2024届浙江省金华十校高三上学期11月模拟考试_浙江省金华十校2024届高三上学期11月模拟考试物理

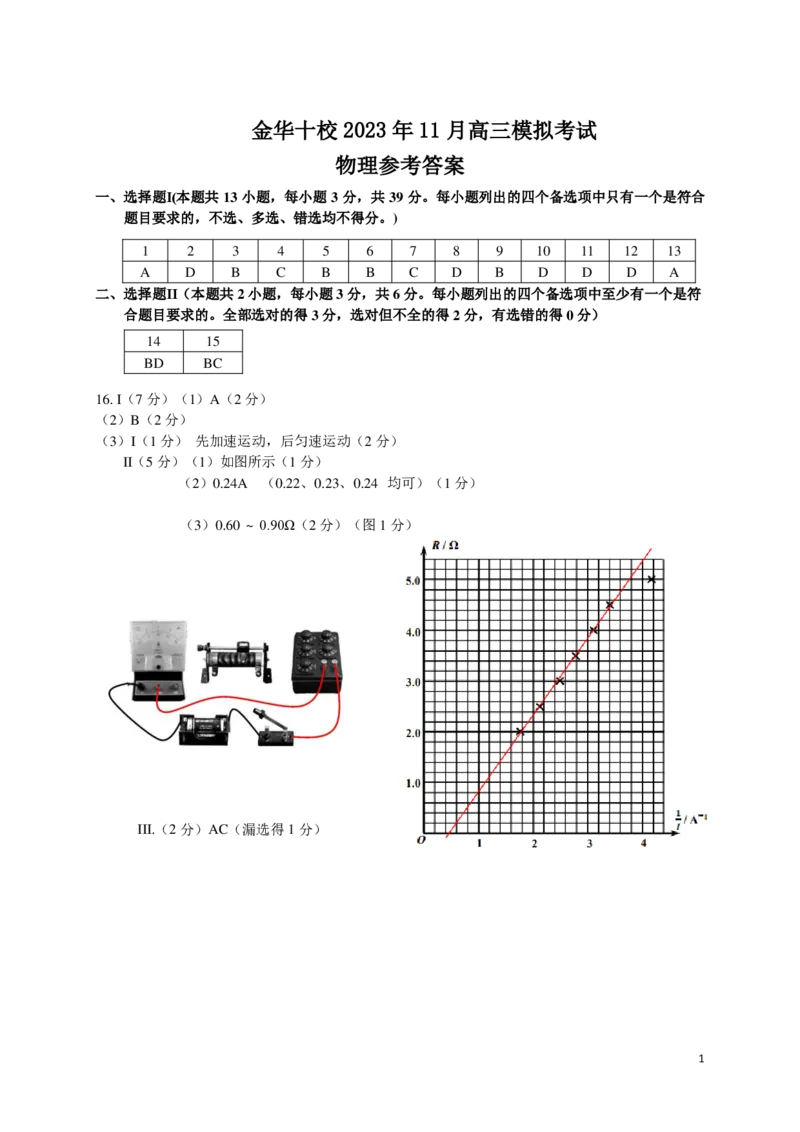
金华十校 2023 年 11 月高三模拟考试 物理参考答案 一、选择题Ⅰ(本题共 13 小题，每小题 3 分，共 39 分。每小题列出的四个备选项中只有一个是符合 题目要求的，不选、多选、错选均不得分。) 1 2 3 4 5 6 7 8 9 10 11 12 13 A D B C B B C D B D D D A 二、选择题Ⅱ（本题共2小题，每小题3分，共6分。每小题列出的四个备选项中至少有一个是符 合题目要求的。全部选对的得3分，选对但不全的得2分，有选错的得0分） 14 15 BD BC 16. I（7分）（1）A（2分） （2）B（2分） （3）I（1分） 先加速运动，后匀速运动（2分） II（5分）（1）如图所示（1分） （2）0.24A （0.22、0.23、0.24 均可）（1分） （3）0.60 ~ 0.90Ω（2分）（图1分） III.（2分）AC（漏选得1分） 1 {#{QQABJY6QoggoQBAAAQhCAwHgCAGQkACCCIoGAAAIIAABABFABAA=}#}17.（8分）（1）温度为T 时，对活塞，根据平衡条件有mgp S2k0.25HpS（1分）解得 0 0 pp （1分） 0 （2）活塞恰好到达气缸顶部的过程中，气体压强体积温度都在变化，则末状态的压强关系为 5 mgp S2k0.25H pS解得：p p （1分） 0 3 0 p 0.5HS PHS 10 根据理想气体状态方程 0  （1分）解得:T  T （1分） T T 3 0 0 （3）第一解法：对活塞由动能定理：（mgPS）0.5HW 0（1分） 0 2 解得：W  p SH （1分） 3 0 2 根据热力学第一定律可得U QW Q PSH（1分） 3 0 第二解法：当气体温度为T 时，体积为0.5HS；当活塞恰好到达气缸顶部时，气体温度升高 0 的过程中，气体做体积变大压强变大的变化，在这个过程中，压强关于上升高度成线性关系，故有 P P 2 气体对外做功为W  0 0.5SH  p SH（2分） 2 3 0 2 根据热力学第一定律可得U QW Q PSH（1分） 3 0 18.（11分）（1）弹珠恰好进入管道，由平抛运动规律，有 Lvt 1 （1分） 解得v4m/s（1分） 2RH  gt2 2 1 1 由能量守恒定律，有 mv 2  mv2 2mgR（1分） 解得v 6m/s（1分） 2 0 2 0 （2）设小弹珠碰前的速度为v ，由能量守恒，有v  v 2 2gh 5m/s（1分） 1 1 0 碰撞时动量守恒，碰后共同速度为v ，mv (M m)v （1分） v 1m/s（1分） 2 1 2 2 1 1 最大弹性势能E  mv 2  (M m)v 22J （1分） P 2 1 2 2   1 1 2 1 2 （3）根据弹性碰撞，有mv Mv mv （1分） mv2  Mv  mv （1分） 1 2 1 2 1 2 2 2 1  (mM) 解得v  v 3m/s 向右运动 （1分得到 3m/s 即可给分） 1 mM 1 2 {#{QQABJY6QoggoQBAAAQhCAwHgCAGQkACCCIoGAAAIIAABABFABAA=}#}19.（11分）（1）由法拉第电磁感应定律可知，开关闭合时感应电动势：   E  （或E n ） （1分） t t B E  LL 0.05V （1分） t 1 2 E 导体棒cd的电流：I  0.0625A （1分） 2R （2）导体棒做加速度减小的加速运动，当通过导体棒的电流为零时，即穿过回路的磁通量为零时导 体棒的速度达到稳定，导体棒做匀速直线运动 回路磁通量不变，即 BLL  B Lvt （2分） 1 1 2 2 1 1 B （建议写出E  1 LL 或E  B Lv 或E E 或 ，可酌情给分，但要有B和L的脚标。具体由阅卷 1 t 1 2 2 2 1 1 1 2 1 2 组长统一标准。） 代入数据接解得，导体棒cd离开水平导轨时的速度：v 1m/s（2分） 1 （3）导体棒离开水平轨道后，从离开到落地的时间t＝0.2s 在水平方向做匀速直线运动，水平位移 x vt，解得x ＝0.2m（1分） 1 1 1 两导体棒在相互作用过程中系统动量守恒mv 2mv ，解得v 0.5m/s（1分） 1 2 2 B 2L2x 对导体棒 ef 应用动量定理 B IL t mv 3 1 2 mv ，解得 x 1m （1 分） 3 1 2， 2R 2 2 x x x 1.2m（1分） 1 2 3 {#{QQABJY6QoggoQBAAAQhCAwHgCAGQkACCCIoGAAAIIAABABFABAA=}#}20. （11分）（1）粒子在电场中做类平抛运动 L v t 0 v 解得v v v  2v （1分） 0.5L  x t x 0 0 2 Eq L mv 2 水平方向由运动学公式可知v 2  2ax 2  ，解得 E  0 （1分） 0 m 2 qL L （2）A到o的运动时间t  ，在磁场中运动时，由几何关系可知轨道半径为r  2L，（1分） 1 v 0 1 1 2 2L L L2L 运动时间为t  T    ，从A到P运动的总时间为t  （1分） 2 4 4 2v 2v 2v 0 0 0 v2 mv 带电粒子在磁场中做匀速圆周运动Bqv  m ， 解得 B  0 （1分） r qL （3）当磁感应强度为0.5B时，带电粒子的运动半径为R 2 2L，分析可得带电粒子将垂直打在屏 1 P上方的某点，设为M点，由几何关系可得PM (2 22)L（1分） 2 当磁感应强度为2B时，带电粒子的运动半径为R  L，分析可得带电粒子打不到屏。 2 2 当粒子轨迹与屏相切时，为屏上的最低点，设为N点，这时圆的半径为R ,由几何关系 3 2 R  R 2L 可得R （42 2）L （1分） PN (2 22)L（1分） 3 2 3 3 故粒子可打到屏上范围为P点上下(2 22)L的范围。 （4）带电粒子从O点到Q点，向右为正方向，由水平方向应用动量定理 Bqv t mv mv y Qx 0 0.5BqLmv mv （1分） 解得v 0.5v Qx 0 Qx 0 1 1 根据动能定理0.5EqL mv 2  m( 2v )2（1分） 解得 v  3v 2 Q 2 0 Q 0 v 3 粒子打在Q点时速度方向与水平方向的夹角为，cos Qx 解得cos （1分） v 6 Q 4 {#{QQABJY6QoggoQBAAAQhCAwHgCAGQkACCCIoGAAAIIAABABFABAA=}#}