2025届高三物理一轮复习考点精练讲义_2024-2025高三（6-6月题库）_2024年08月试卷_08122025届高三物理一轮复习考点精练讲义

2025 届高三物理一轮复习考点精练讲义 目录 第1讲 运动的描述........................................................................................................................................3 考点一 对质点和参考系的理解 位移与路程................................................................................3 考点二 平均速度和瞬时速度..........................................................................................................5 考点三 速度、速度变化量和加速度的关系..................................................................................8 考点四 “匀速运动”模型的实际应用........................................................................................9 第2讲 匀变速直线运动规律的应用..........................................................................................................21 考点一 匀变速直线运动公式的应用............................................................................................21 考点二 常用的“六种”物理思想方法........................................................................................24 考点三 自由落体运动和竖直上抛运动........................................................................................27 第3讲 重力 弹力 摩擦力..........................................................................................................................46 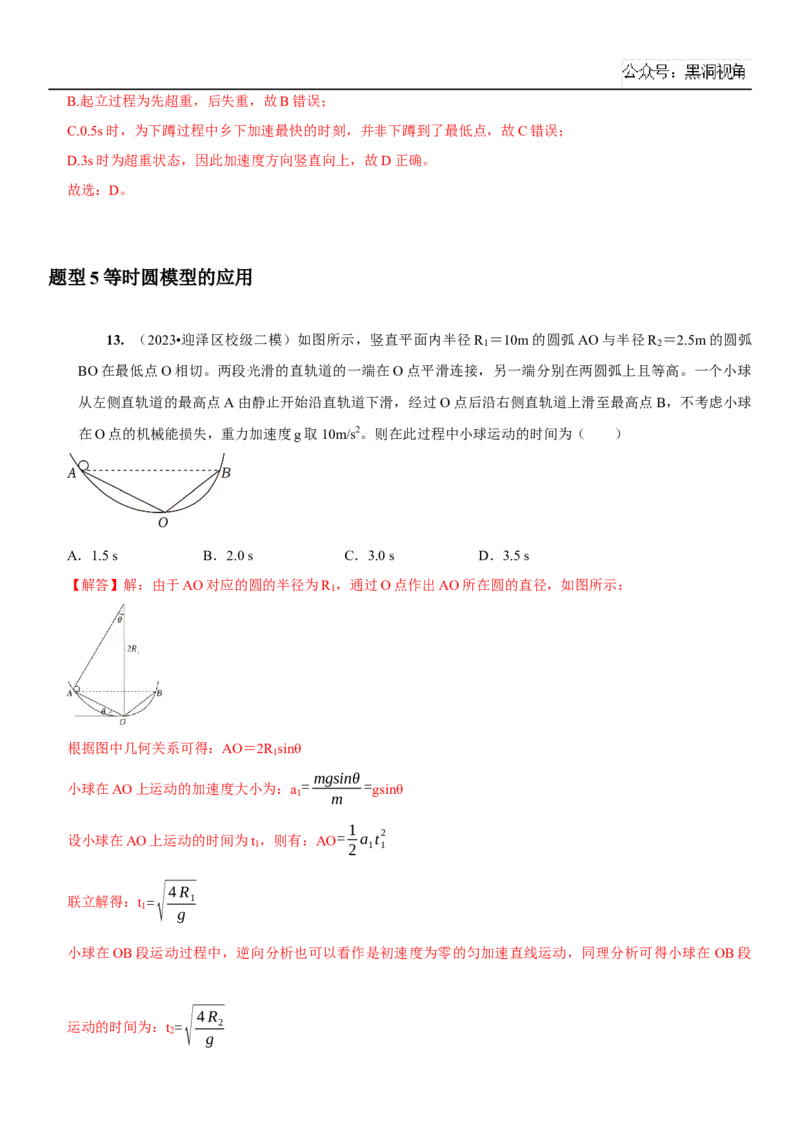考点一 弹力的分析与计算............................................................................................................46 考点二 滑轮模型与死结模型问题................................................................................................49 考点三 摩擦力的分析与计算........................................................................................................51 考点四 摩擦力的突变问题............................................................................................................54 第4讲 力的合成和分解..............................................................................................................................69 考点一 共点力的合成....................................................................................................................69 考点二 力分解的两种常用方法....................................................................................................71 考点三 力的合成与分解方法在实际问题中的应用....................................................................73 第5讲 受力分析 共点力的平衡................................................................................................................87 考点一 整体与隔离法的应用........................................................................................................87 考点二 处理平衡问题常用的“三种”方法处理平衡问题的常用方法....................................90 考点三 动态平衡问题的处理技巧................................................................................................93 考点四 平衡中的临界与极值问题................................................................................................95第6讲 牛顿第一定律 牛顿第三定律......................................................................................................108 考点一 牛顿第一定律的理解与应用..........................................................................................108 考点二 牛顿第三定律的理解与应用..........................................................................................110 考点三 “转移研究对象法”在受力分析中的应用..................................................................112 第7讲 牛顿第二定律 两类运动学问题..................................................................................................121 考点一 瞬时加速度的求解..........................................................................................................121 考点二 动力学中的图象问题......................................................................................................124 考点三 连接体问题......................................................................................................................125 考点四 动力学两类基本问题......................................................................................................128 第8讲 曲线运动 运动的合成与分解......................................................................................................145 考点一 物体做曲线运动的条件及轨迹......................................................................................145 考点二 运动的合成及运动性质分析..........................................................................................147 考点三 小船渡河模型..................................................................................................................149 考点四 绳(杆)端速度分解模型...................................................................................................152 第9讲 抛体运动........................................................................................................................................166 考点一 平抛运动的基本规律......................................................................................................166 考点二 斜面上的平抛运动问题..................................................................................................169 考点三 平抛运动的临界问题......................................................................................................172 考点四 类平抛运动模型..............................................................................................................175 第10讲 圆周运动......................................................................................................................................190 考点一 圆周运动中的运动学分析..............................................................................................190 考点二 圆周运动中的动力学分析..............................................................................................193 考点三 圆周运动的临界问题......................................................................................................196 考点四 竖直平面内圆周运动绳、杆模型..................................................................................199第 1 讲 运动的描述 1、知道物体抽象为质点的条件。 2、理解参考系的意义 3、理解位移和路程 4、理解速度、平均速度和瞬时速度 5、理解加速度 考点一 对质点和参考系的理解 位移与路程 1．质点 (1)用来代替物体的有质量的点叫做质点． (2)研究一个物体的运动时，如果物体的形状和大小对问题的影响可以忽略，就可以看做质点． (3)质点是一种理想化模型，实际并不存在． 2．参考系(1)参考系可以是运动的物体，也可以是静止的物体，但被选为参考系的物体，我们都假定它是静止的． (2)比较两物体的运动情况时，必须选同一参考系． (3)选取不同的物体作为参考系，对同一物体运动的描述可能不同．通常以地球为参考系． 3．位移和路程的“两点”区别 (1)决定因素不同：位移由始、末位置决定，路程由实际的运动路径决定． (2)运算法则不同：位移应用矢量的平行四边形定则运算，路程应用标量的代数运算． [例题1] （2024•下城区校级模拟）质点是一个理想化模型，下列说法中正确的是（ ） A．研究月球绕地球的运动轨迹时，月球不可看作质点 B．研究刘翔110m栏比赛的跨栏技术时，其身体可看作质点 C．研究火车通过隧道所需的时间时，火车不可看作质点 D．研究“嫦娥一号”在轨道上的飞行姿态时，“嫦娥一号”可看作质点 【解析】A、研究月球绕地球的运动轨迹时，月球的大小相对于和地球之间的距离来说是很小的，可以忽略， 此时月球可看作质点，故A错误； B、研究刘翔110m栏比赛的跨栏技术时，需要分析人的不同的动作，所以此时人不能看成质点，故B错误； C、研究火车通过隧道所需的时间时，火车的长度相对于隧道来说是不能忽略的，所以此时的火车不能看成质 点，故C正确； D、研究“嫦娥一号”在轨道上的飞行姿态时，看的就是它的形状如何，所以不能看成质点，故D错误。 故选：C。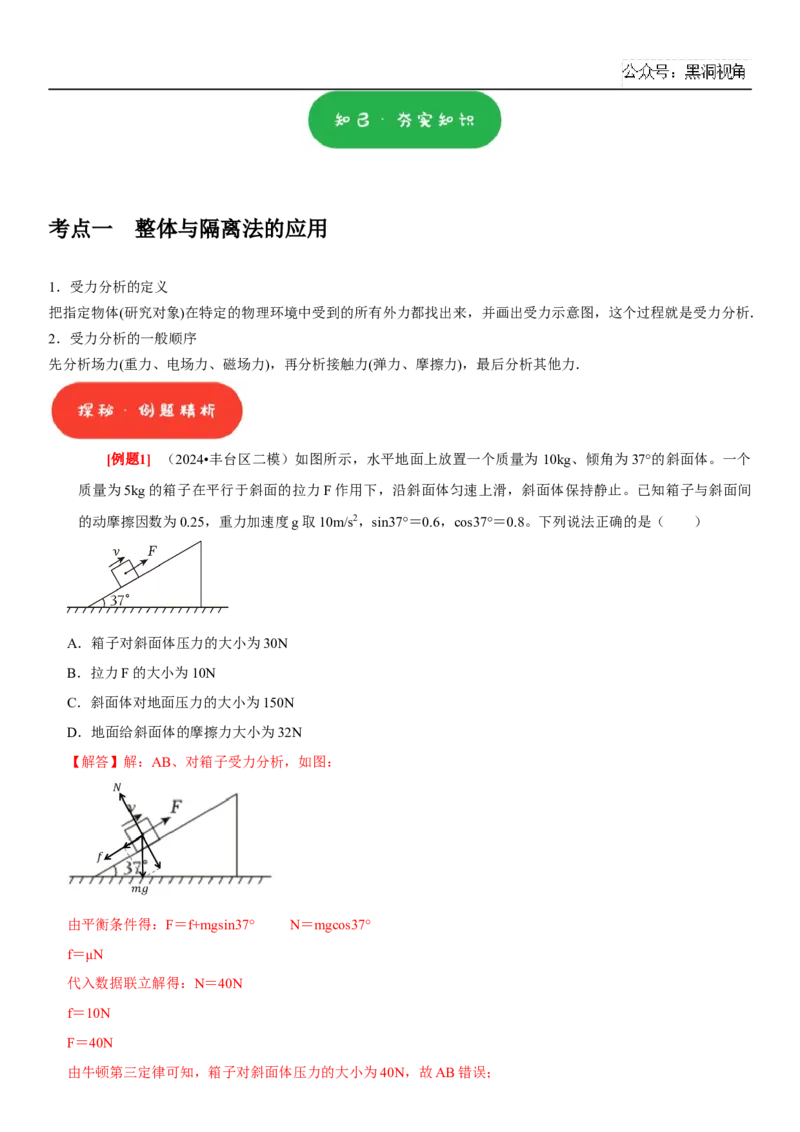 [例题2] （2024•汕头一模）汕头海湾隧道全长6680米，线路如图所示，其中AB、CD段可以看作直线 路段，BC段可以看作曲线路段，下列说法正确的是（ ） A．计算通过BC段所用时间，由于汽车做曲线运动，不能将汽车看作质点 B．计算汽车通过整段隧道所用时间，可以将汽车看作质点 C．测量两辆汽车的超车时间，可以将汽车看作质点 D．研究乘客所受推背感与汽车加速度关系，可以将乘客和汽车视为整体来研究【解析】AB．计算通过BC段所用时间和通过整段隧道所用时间时，汽车的长度对研究目的影响很小，可以忽 略汽车的大小和形状，可以将汽车看作质点，故A错误，B正确； C．测量两辆汽车的超车时间，（本资料来自于公众号：屋里学家）汽车的长度对研究目的影响很大，不可以 忽略汽车的大小和形状，不可以将汽车看作质点，故C错误； D．研究乘客所受推背感与汽车加速度关系，若把乘客和汽车视为整体，无法单独对乘客所受推背感进行分析， 故不能当作整体，故D错误。 故选：B。 [例题3] （2023•鲤城区校级一模）2022年卡塔尔世界杯足球比赛万众瞩目，假定在某次比赛中，足球从 地面被踢出腾空先上升后下落，足球在空中划出了一道弧线。如果不计空气的作用力，从足球被踢出到落地 瞬间，关于这个运动过程，下列说法中正确的是（ ） A．足球运动时一定能看作质点 B．足球的速度变化得越来越快 C．足球前进的水平位移与被踢出时的速度大小和方向有关 D．足球在空中运动的路程越大，则其位移一定越大 【解析】A、如果足球的大小，形状在研究的问题中不能忽略，足球不能被看作质点，例如研究足球的转动， 足球不能看作质点，故A错误； B、由于不计空气的作用力，足球只受到重力的作用，足球的加速度不变，足球的速度变化快慢不变，故 B错 误； C、设足球踢出瞬间速度为v ，（本资料来自于公众号：屋里学家）与水平方向夹角为θ，足球被踢出后做斜抛 0 v sinθ v sinθ v2sin2θ 运动，足球上升到最高点时间为：t= 0 ，足球前进的水平位移：x=2v t=2v cosθ 0 = 0 ， g x 0 g g 可知足球前进的水平位移与被踢出时的速度大小和方向有关，故C正确； D、若足球的水平速度很小，足球在空中运动的路程越大，足球的水平位移很小，则其位移不一定越大，故D 错误。 故选：C。考点二 平均速度和瞬时速度 1．平均速度 (1)在变速运动中，物体在某段时间内的位移与发生这段位移所用时间的比值叫做这段时间内的平均速度，即v＝， 其方向与位移的方向相同． (2)平均速度反映一段时间内物体运动的平均快慢程度，它与一段时间或一段位移相对应． 2．瞬时速度 (1)运动物体在某一时刻(或某一位置)的速度，方向沿轨迹上物体所在点的切线方向指向前进的一侧，是失量．瞬时 速度的大小叫速率，是标量． (2)瞬时速度能精确描述物体运动的快慢，它是在运动时间Δt→0时的平均速度，与某一时刻或某一位置相对应． (3)平均速率是路程与时间的比值，它与平均速度的大小没有对应关系． [例题4] （2024•湖州模拟）酒店内的智能机器人可以把1楼大厅的外卖送至指定楼层的客房。如图为机 器人送餐至9楼的场景。下列说法正确的是（ ） A．在避开障碍物的过程中，可以把机器人看成质点 B．记录机器人从1楼至9楼的时间，可以把机器人看成质点 C．送餐的全过程，机器人的位移大小可能等于路程 D．若送餐用时625s，行程50m，机器人的平均速度大小为0.08m/s 【解析】AB、物体看作质点的条件是物体的形状、大小对所研究的问题没有影响，或者影响很小。在避开障碍 物的过程中要注意机器人的各部分是否会与障碍物接触，（本资料来自于公众号：屋里学家）所以不能将机器 人看作质点；但是在记录机器人从1楼运动到9楼的时间时，可以将机器人看作质点，故A错误，B正确； C、送餐的全过程，机器人的运动轨迹不是直线，所以位移大小小于路程，不可能等于路程，故C错误； s 50 D、若送餐用时625s，行程50m，根据平均速率公式可知，机器人的平均速率为v= = m/s=0.08m/s， t 625 因为不知道机器人的位移，所以无法计算其平均速度大小，故D错误。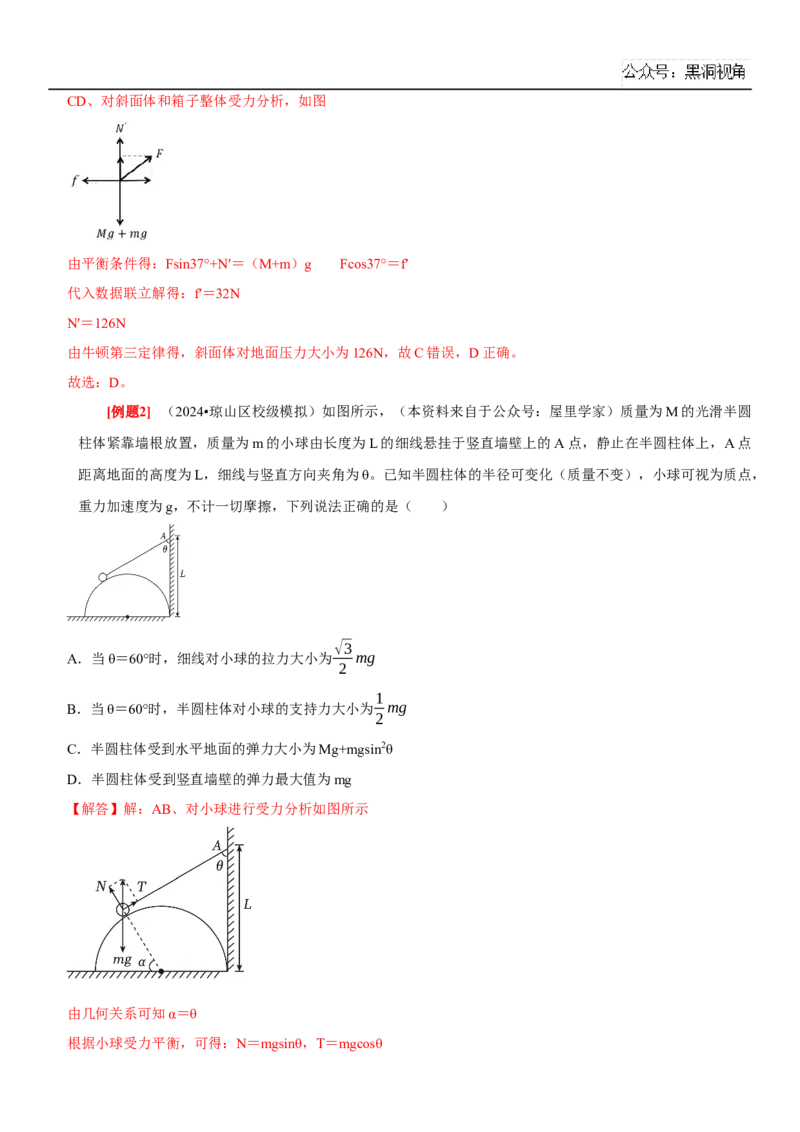 故选：B。[例题5] （2023•重庆模拟）如题图为太极练功场示意图，半径为 R的圆形场地由“阳鱼（白色）”和 “阴鱼（深色）”构成，O点为场地圆心。其内部由两个圆心分别为O 和O 的半圆弧分隔。某晨练老人从A 1 2 点出发沿“阳鱼”和“阴鱼”分界线走到B点，用时为t，下列说法正确的是（ ） A．t指的是走到B点的时刻 1 B．老人的位移为 πR 2 2R C．老人的平均速度为 t πR D．老人的平均速率为 2t 【解析】A．用时为t，可知t指的是人从A走到B点的时间间隔，不是时刻，故A错误； B．位移大小指始位置指向末位置的有向线段的长度，则老人的位移为AB连线的长度，即位移大小为2R，故 B错误； x 2R C．老人的位移为x＝2R，则由平均速度公式可得，老人的平均速度为v= = ，故C正确； t t R s πR D、老人经过的路程s＝2π× =πR，故平均速率v= = ，故D错误。 2 t t 故选：C。 [例题6] （2023•镇海区模拟）平潭海峡公铁两用大桥全长16.34km，该大桥所处的平潭海峡是世界三大 风暴海域之一，以“风大、浪高、水深、涌急”著称。为保证安全起见，环境风速超过20m/s时，列车通过 该桥的运行速度不能超过300km/h，下列说法正确的是（ ） A．题目中“全长16.34km”指的是位移大小 B．“风速超过20m/s”“不能超过300km/h”中所指的速度均为瞬时速度 C．“风速超过20m/s”指的是平均速度，“不能超过300km/h”指的是瞬时速度 D．假设某火车通过该大桥所用时间为0.08h，则平均速度约为204km/h 【解析】A.题目中“全长16.34km”指的是该大桥的长度，指路程大小，不是位移大小，故A错误； BC.“风速超过20m/s”“不能超过300km/h”中均指的是某一时刻的速度，均为瞬时速度，故B正确，C错误； D．由于不清楚题目中所述的通过大桥的位移，所以无法计算平均速度，故D错误。 故选：B。[例题7] （2024•琼山区校级模拟）关于速度、速度的变化量、加速度，下列说法中正确的是（ ） A．物体运动时速度的变化量越大，它的加速度一定越大 B．速度很大的物体，其加速度可以为零 C．某时刻物体速度为零，其加速度不可能很大 D．加速度很大时，运动物体的速度一定很快变大 【解析】A、物体的速度变化大，但所需时间更长的话，物体速度的变化率可能很小，则加速度就会很小，故 A错误； B、运动物体的速度很大，其加速度可能为零，例如匀速直线运动，故B正确； C、运动物体的速度为零，其加速度可能很大，刚开始发射的火箭，故C错误。 D、加速度很大时，其运动物体的速度变化一定越快，而不是速度一定很快变大，故D错误； 故选：B。 考点三 速度、速度变化量和加速度的关系 1．速度 (1)物理意义：描述物体运动快慢和方向的物理量，是状态量． (2)定义式：v＝ (3)决定因素：v的大小由v、a、Δt决定． 0 (4)方向：与位移同向，即物体运动的方向． 2．速度变化量 (1)物理意义：描述物体速度改变的物理量，是过程量． (2)定义式：Δv＝v－v. 0 (3)决定因素：Δv由v与v 进行矢量运算得到，由Δv＝aΔt知Δv由a与Δt决定． 0 (4)方向：由Δv或a的方向决定． 3．加速度 (1)物理意义：描述物体速度变化快慢和方向的物理量，是状态量． (2)定义式：a＝＝ (3)决定因素：a不是由v、Δt、Δv来决定，而是由来决定． (4)方向：与Δv的方向一致，由F的方向决定，而与v、v的方向无关． 0 [例题8] （2024•庆云县校级模拟）某汽车进行性能测试，在平直的路面上由静止开始运动，0～5s内的 位移—时间图像如图所示，该图线在0～t 时间内是抛物线的一部分，t ～5s时间内是直线，两部分平滑相连。 1 1 下列说法正确的是（ ）A．汽车的最大速度为30m/s B．汽车加速过程的时间为1.5s C．汽车加速过程的加速度大小为20m/s2 D．汽车1s末的速度大小为20m/s v 【解析】AB.设t 时刻的速度为v，0～t 汽车做匀加速运动，根据平均速度公式，得汽车位移x = t ＝30m；t 1 1 1 2 1 1 ～5s汽车做匀速运动，（本资料来自于公众号：屋里学家）得汽车位移x ＝v（5﹣t ）＝120m﹣30m＝90m， 2 1 联立解得v＝30m/s，t ＝2s，故A正确，B错误。 1 v 30 CD.根据加速度的定义，汽车加速度为 a = = m/s2＝15m/s2，根据速度公式汽车在 1s末的速度v ＝at ＝ t 2 1 2 1 15×1m/s＝15m/s，故CD错误。 故选：A。 [例题9] （2023•思明区校级模拟）随着新能源轿车的普及，人们对车辆乘坐的舒适性要求越来越高。加 速度对时间的变化率物理学中称之为“加加速度”，通常用符号“j”表示，如果j值过大，会形成冲击力，影 响乘客乘坐的舒适性。对汽车来说，人体可以承受的j值通常在0.4～1.0之间。如图为某国产新能源轿车，测 得其启动后a与时间t的变化关系为a＝3﹣0.5t，则（ ） A．国际单位制中“加加速度”的单位应是m/s2 B．j为0的运动一定是匀速直线运动 C．该汽车启动后做匀变速直线运动 D．该汽车启动后j的值大小为0.5 Δa m/s2 【解析】A、根据“加加速度”的定义j= ，可知国际单位制中“加加速度”的单位应是 =m/s3，故A Δt s 错误； B、j＝0，表示加速度没有发生变化，（本资料来自于公众号：屋里学家）即加速度是恒定的，所以汽车应该做匀变速直线运动，故B错误； C、汽车启动后a与时间t的变化关系为a＝3﹣0.5t，可知加速度是随时间变化的，所以该汽车启动后做变加速 直线运动，故C错误； D、根据汽车启动后a与时间t的变化关系a＝3﹣0.5t，可知其斜率表示“加加速度”，斜率为﹣0.5，所以该汽 车启动后j的值大小为0.5，故D正确。 故选：D。 考点四 “匀速运动”模型的实际应用 1．模型介绍 “匀速运动”是一种理想化模型，是最基本、最简单的运动，且应用广泛．例如：声、光的传播都可以看成匀速， 而实际生活中的运动估算，也经常用到这一模型，如计算飞行时间。 2．分析方法 在这类问题中位移的计算是关键，有时要巧用几何关系(如光波、声波反射、折射问题，如图2)，有时要估算长度 (如高速摄影，如图3)，有时要求相对位移(如动态测速)等．这类问题的核心方程只有一个：v＝. 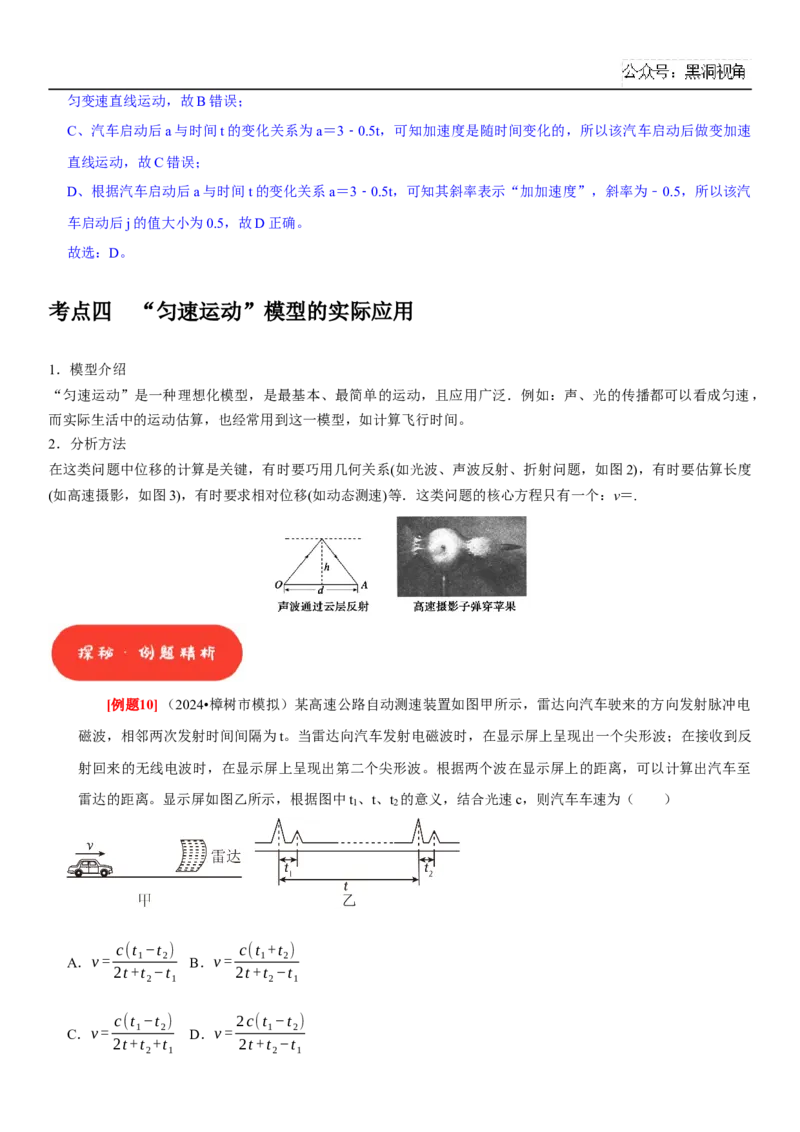[例题10]（2024•樟树市模拟）某高速公路自动测速装置如图甲所示，雷达向汽车驶来的方向发射脉冲电 磁波，相邻两次发射时间间隔为t。当雷达向汽车发射电磁波时，在显示屏上呈现出一个尖形波；在接收到反 射回来的无线电波时，在显示屏上呈现出第二个尖形波。根据两个波在显示屏上的距离，可以计算出汽车至 雷达的距离。显示屏如图乙所示，根据图中t 、t、t 的意义，结合光速c，则汽车车速为（ ） 1 2 c(t −t ) c(t +t ) A．v= 1 2 B．v= 1 2 2t+t −t 2t+t −t 2 1 2 1 c(t −t ) 2c(t −t ) C．v= 1 2 D．v= 1 2 2t+t +t 2t+t −t 2 1 2 1t 【解析】第一次发射电磁波，知汽车距离雷达的距离为x ＝c 1，第二次发射电磁波，知汽车距离雷达的距离为 1 2 t x ＝c 2， 2 2 t t 两次反射无线电波的时间间隔为 Δt=t+ 2− 1，汽车的位移 Δx＝x ﹣x ， 1 2 2 2 Δx c(t −t ) 汽车车速 v= 得 v= 1 2 ，故A正确，BCD错误。 Δt 2t+t −t 2 1 故选：A。 [例题11] （2024•琼山区校级模拟）天空有近似等高的云层，为了测量其高度，在水平地面上与观测者的 距离d＝3.0km处进行了一次爆炸，观测者听到由空气直接传来的爆炸声和云层反射来的爆炸声，在时间上相 1 差Δt＝6.0s，已知空气中的声速v= km/s．试估计云层下表面的高度． 3 【解析】如图，A表示爆炸处，O表示反射点，S表示观测者所在处，h表示云层下表面的高度．用t 表示爆炸 1 声从A直接传到s处所经时间，则有d＝vt 1 …① 用t 表示爆炸声经云层反射到达s处所经历时间，因为入射角等于反射角，故有 2 √ d 2 2 ( ) + ℎ 2=vt 2 …② 2 已知t 2 ﹣t 1 ＝Δt …③ 联立①②③式，可得 1 h= √(vΔt) 2+2dvΔt 2 1 √ 1 代入数值得h= × ( ×103×6) 2+2×3×103×6=2.0×103m 2 3 答：云层下表面的高度为2.0×103m．题型1质点、参考系、位移与路程 1. （2023•浙江模拟）海军航空大学某基地组织飞行训练，歼﹣15战机呼啸天空，与空中的月亮同框， 形成“飞鲨逐月”的浪漫景象，如图为摄影师在同一位置前后拍下两张照片，下列说法正确的是（ ） A．以月亮为参考系，战机是静止的 B．以战机里的飞行员为参考系，战机是运动的 C．两次拍摄相差20秒钟，这20秒是指时间间隔 D．研究战机在空中的飞行姿态，可以把战机看作质点 【解析】A．战机的运行速度和月亮的运行速度并不相同，所以以月亮为参考系，战机是运动的，故A错误；； B．飞行员相对战机是不动的，（本资料来自于公众号：屋里学家）所以以战机里的飞行员为参考系，战机是 静止的，故B错误； C．两次拍摄相差20秒钟，这20秒是指时间间隔，故C正确； D．研究空中飞行姿态时，其大小形状不可忽略，所以不能将战机看作质点，故D错误。 故选：C。 2. （2022•莆田二模）2021年5月15日，“天问一号”火星探测器平稳着陆火星；5月22日10： 40，“祝融号”火星车安全驶离着陆平台到达火星表面，开始巡视探测，至12月31日，“祝融号”火星车 累计行驶突破1400m。下列叙述正确的是（ ） A．“5月22日10：40”指的是时间 B．“1400m”指的是“祝融号”火星车的位移大小 C．从地球到火星，“祝融号”火星车的惯性发生改变 D．研究“祝融号”火星车在火星表面的运行轨迹时，可将其视为质点 【解析】A、“5月22日10：40”指的是时间点，是时刻，故A错误； B、“1400m”指的是“祝融号”火星车的路程大小，故B错误； C、惯性只和质量有关，在地球和在火星，“祝融号”火星车的质量不变，故惯性不变，故C错误； D、研究“祝融号”火星车在火星表面的运行轨迹时，火星车的大小和形状对所研究的问题没有影响，故可将 其视为质点，故D正确； 故选：D。题型2平均速度 速度 3. （2023•镇海区模拟）平潭海峡公铁两用大桥全长16.34km，该大桥所处的平潭海峡是世界三大风暴 海域之一，以“风大、浪高、水深、涌急”著称。（本资料来自于公众号：屋里学家）为保证安全起见，环 境风速超过20m/s时，列车通过该桥的运行速度不能超过300km/h，下列说法正确的是（ ） A．题目中“全长16.34km”指的是位移大小 B．“风速超过20m/s”“不能超过300km/h”中所指的速度均为瞬时速度 C．“风速超过20m/s”指的是平均速度，“不能超过300km/h”指的是瞬时速度 D．假设某火车通过该大桥所用时间为0.08h，则平均速度约为204km/h 【解析】A.题目中“全长16.34km”指的是该大桥的长度，指路程大小，不是位移大小，故A错误； BC.“风速超过20m/s”“不能超过300km/h”中均指的是某一时刻的速度，均为瞬时速度，故B正确，C错误； D．由于不清楚题目中所述的通过大桥的位移，所以无法计算平均速度，故D错误。 故选：B。 4. （2023•丽水二模）2022年11月30日，“神舟十五号”飞船和空间站“天和”核心舱成功对接，整 个对接过程历时约6.5h，对接后速度约为7.68km/s，则（ ） A．“6.5h”指的是时刻 B．“7.68km/s”为平均速度 C．研究如何实现对接时，可将“天和”视为质点 D．对接成功后，“神舟十五号”相对地球是运动的 【解析】A、“6.5h”指的是时间间隔，故A错误； B、“7.68km/s”为瞬时速度的大小，故B错误； C、研究如何实现对接时，要考虑“天和”的形状和大小，不能忽略“天和”的形状和大小，所以不可以将 “天和”视为质点，否则无法实现对接，故C错误； D、以地球为参照，对接成功后，则“神舟十五号”相对地球是运动的，故D正确。 故选：D。题型3加速度的计算 5. （2023•琼山区校级二模）轿车的加速度变化影响乘客的舒适度，加速度变化率越小，乘坐轿车的人 感到越舒适。加速度变化率是描述加速度随时间变化快慢的物理量，其单位为（ ） A．m/s B．m/s2 C．m/s3 D．m/s4 【解析】新物理量表示的是加速度变化的快慢，所以新物理量应该等于加速度的变化量与时间的比值，而加速 Δa 度的单位是m/s2，由 可知，新物理量的单位应该是m/s3，故C正确，ABD错误。 Δt 故选：C。 6. （2023•重庆模拟）下列几种运动中，实际中不可能存在的是（ ） A．物体的速率不变，但加速度不为零 B．物体的速度越来越小，加速度越来越大 C．物体的加速度越来越小，速度越来越大 D．物体的加速度不变（不为零），速度也保持不变 【解析】A、物体的速率不变，但加速度不为零是可能的，例如匀速圆周运动，故A错误； B、当加速度与速度反向，则物体做减速运动，速度越来越小，加速度可能变大也可能变小，故B错误； C、当加速度与速度同向，则物体做加速运动，速度越来越大，加速度可能变大也可能变小，故C错误； D、若加速度不为零，则速度一定发生变化，故D不可能，符合题意。 故选：D。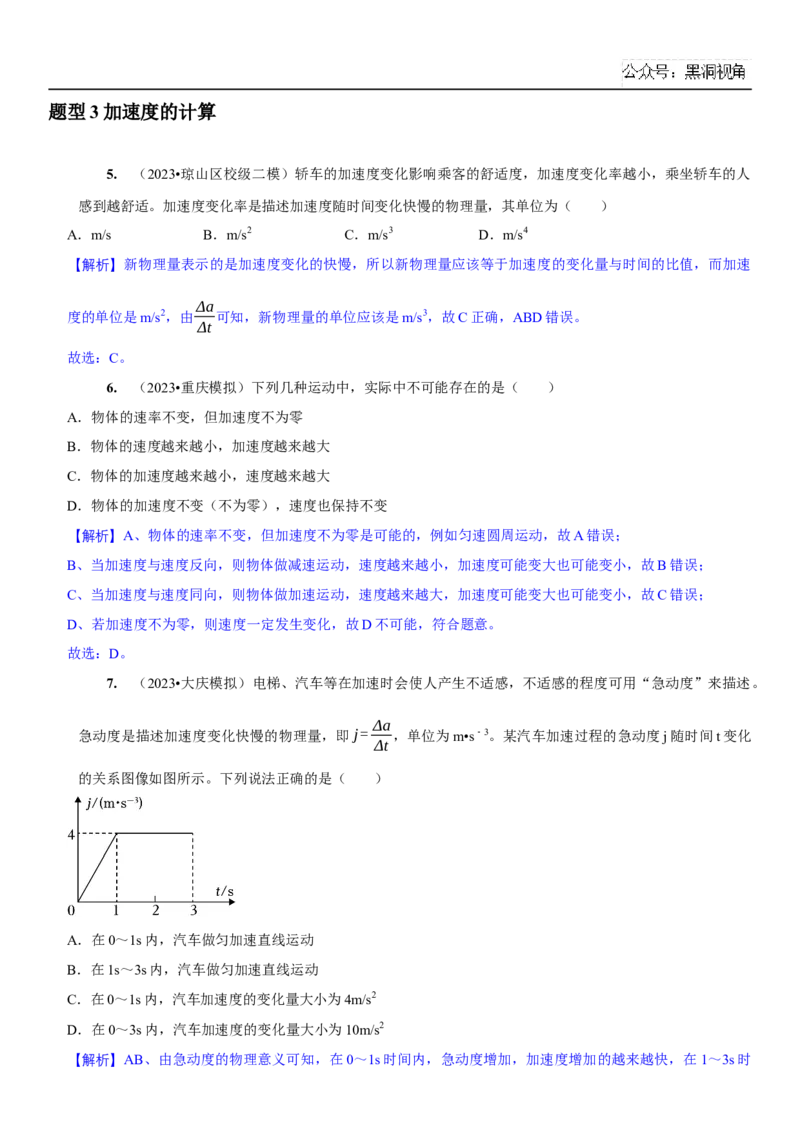 7. （2023•大庆模拟）电梯、汽车等在加速时会使人产生不适感，不适感的程度可用“急动度”来描述。 Δa 急动度是描述加速度变化快慢的物理量，即j= ，单位为m•s﹣3。某汽车加速过程的急动度j随时间t变化 Δt 的关系图像如图所示。下列说法正确的是（ ） A．在0～1s内，汽车做匀加速直线运动 B．在1s～3s内，汽车做匀加速直线运动 C．在0～1s内，汽车加速度的变化量大小为4m/s2 D．在0～3s内，汽车加速度的变化量大小为10m/s2 【解析】AB、由急动度的物理意义可知，在0～1s时间内，急动度增加，加速度增加的越来越快，在1～3s时间内，急动度不变，则加速度均匀增加，即加速度总是在增大的，汽车一直做加速度增大的加速运动，故 AB 错误； C、由急动度的物理意义可知，j﹣t图象的面积代表加速度的变化量，在0～1s时间内，汽车加速度的变化量大 1 小为：Δa= ×1×4m/s2＝2m/s2，故C错误； 2 1 D、急 j﹣t 图象的面积代表加速度的变化量，在 0～3s 时间内，汽车加速度的变化量大小为：Δa= × 2 1×4m/s2+4×（3﹣1）m/s2＝10m/s2，故D正确。 故选：D。 8. 如图甲所示，火箭发射时，速度能在10s内由0增加到100m/s；如图乙所示，汽车以108km/h的速度 行驶，急刹车时能在2.5s内停下来，下列说法中正确的是（ ） A．10s内火箭的速度变化量为10m/s B．2.5s内汽车的速度变化量为﹣30m/s C．火箭的速度变化比汽车的快 D．火箭的加速度比汽车的加速度大 【解析】A、火箭的速度变化量Δv＝v﹣v ＝100﹣0m/s＝100m/s，故A错误； 0 108 B、汽车的速度变化量Δv＝v﹣v =0− m/s=−30m/s，故B正确； 0 3.6 Δv 100 −30 CD、据a= ，得火箭的加速度a = m/s2=10m/s2 ，汽车的加速度a = m/s2=−12m/s2 ，负 Δt 火 10 汽 2.5 号表示加速度的方向与速度方向相反，加速度的大小为a =12m/s2 ，由此可知汽车的加速度大，速度变化快， 汽 故CD均错误。 故选：B。题型4速度、速度变化量和加速度的关系 9. （2023•福州模拟）下列说法正确的是（ ） A．加速度为正值，物体一定做加速直线运动 B．百米比赛时，运动员的冲刺速度越大成绩越好 C．做直线运动的物体，加速度为零时，速度不一定为零，速度为零时，加速度一定为零 D．相对于某参考系静止的物体，对地速度不一定为零 【解析】A、加速度为正值，只是说明与规定的正方向相同，不一定与速度方向相同，不一定是加速运动，故 A错误； B、根据平均速度的定义可知，百米比赛时，运动员的平均速度越大，用时越短，成绩越好，故C错误； C、加速度是描述速度变化快慢的物理量，做直线运动的物体，加速度为零时，速度不一定为零，速度为零时， 加速度不一定为零，故C错误； D、相对于某参考系静止的物体，对地速度不一定为零，要合理选取参考系，故D正确。 故选：D。 10. 关于加速度的方向，下列描述正确的是（ ） A．一定与速度方向相同 B．一定与速度方向相反 C．一定与速度变化量的方向相同 D．一定与速度变化量的方向相反 Δv 【解析】根据a= 知，加速度方向与速度变化量的方向相同，与初速度方向、末速度的方向可能相同、可能 Δt 相反，可能不在同一条直线上，故C正确，ABD错误。 故选：C。 题型5物体速度变化规律分析 11. （2024•保定一模）如图甲所示，（本资料来自于公众号：屋里学家）一辆小轿车从服务区匝道驶入 平直高速行车道时速率为20m/s，想要加速驶入内车道，由于行车道前方匀速运动的大货车速度较小，影响超 车。小轿车加速8s后放弃超车，立即减速，再经过3s，与大货车同速跟随，再伺机超车。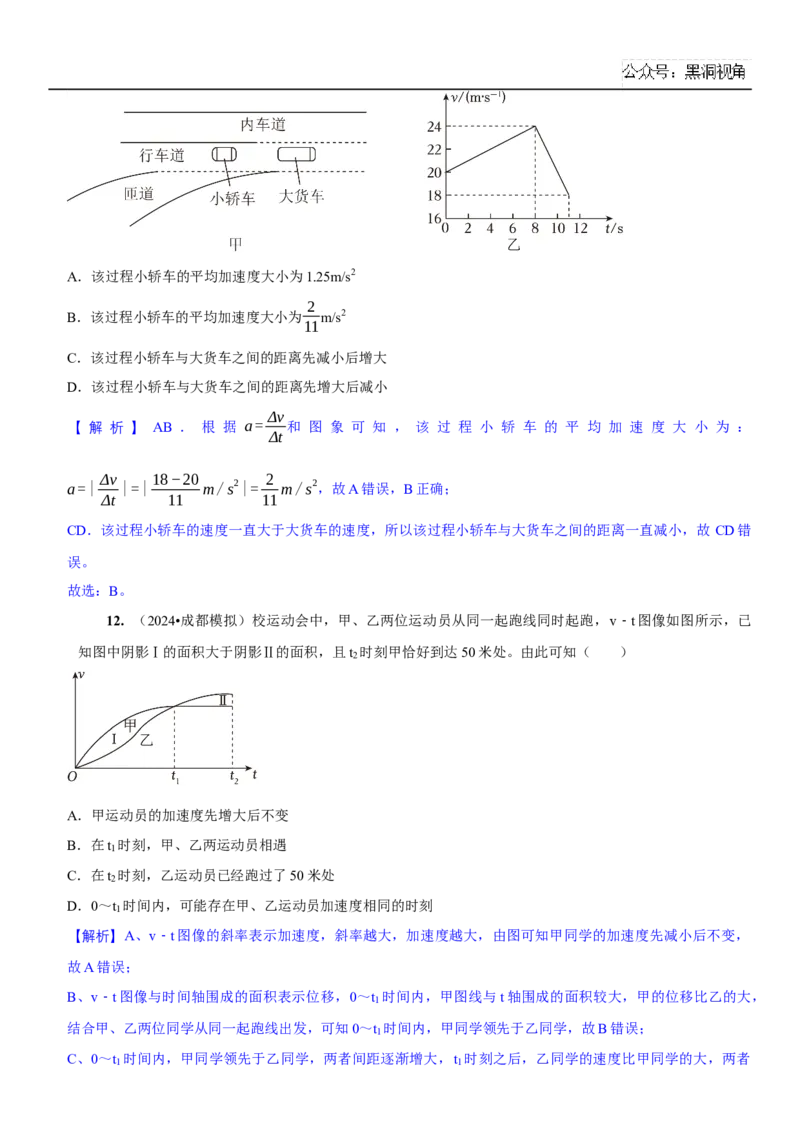该过程小轿车的速 度与时间的关系如图乙所示，下列说法中正确的是（ ）A．该过程小轿车的平均加速度大小为1.25m/s2 2 B．该过程小轿车的平均加速度大小为 m/s2 11 C．该过程小轿车与大货车之间的距离先减小后增大 D．该过程小轿车与大货车之间的距离先增大后减小 Δv 【 解 析 】 AB ． 根 据 a= 和 图 象 可 知 ， 该 过 程 小 轿 车 的 平 均 加 速 度 大 小 为 ： Δt Δv 18−20 2 a=| |=| m/s2|= m/s2，故A错误，B正确； Δt 11 11 CD．该过程小轿车的速度一直大于大货车的速度，所以该过程小轿车与大货车之间的距离一直减小，故 CD错 误。 故选：B。 12. （2024•成都模拟）校运动会中，甲、乙两位运动员从同一起跑线同时起跑，v﹣t图像如图所示，已 知图中阴影Ⅰ的面积大于阴影Ⅱ的面积，且t 时刻甲恰好到达50米处。由此可知（ ） 2 A．甲运动员的加速度先增大后不变 B．在t 时刻，甲、乙两运动员相遇 1 C．在t 时刻，乙运动员已经跑过了50米处 2 D．0～t 时间内，可能存在甲、乙运动员加速度相同的时刻 1 【解析】A、v﹣t图像的斜率表示加速度，斜率越大，加速度越大，由图可知甲同学的加速度先减小后不变， 故A错误； B、v﹣t图像与时间轴围成的面积表示位移，0～t 时间内，甲图线与t轴围成的面积较大，甲的位移比乙的大， 1 结合甲、乙两位同学从同一起跑线出发，可知0～t 时间内，甲同学领先于乙同学，故B错误； 1 C、0～t 时间内，甲同学领先于乙同学，两者间距逐渐增大，t 时刻之后，乙同学的速度比甲同学的大，两者 1 1间距逐渐减小，但由于阴影Ⅰ的面积大于阴影Ⅱ的面积，所以甲到达50m时乙还没有到达50m处，故C错误； D、甲的加速度一开始大于乙的加速度，后来又小于乙的加速度，所以 0～t 时间内，可能存在甲、乙运动员加 1 速度相同的时刻，故D正确。 故选：D。 13. （2024•大庆三模）在跳水训练中，某运动员（可看作质点）t＝0时刻从距水面1m高度处竖直向上 起跳，运动过程中不计空气阻力，其运动的速度与时间关系图像如图所示，规定竖直向下为正方向，g取 10m/s2，则（ ） A．t 时刻运动员进入水面 1 B．t 时刻运动员到达最高点 2 C．运动员在最高点时距水面1.8m D．运动员入水速度为2m/s 【解析】A.结合题意及图像可知，t 时刻为运动员起跳后向上做匀减速直线运动的最终时刻，此时运动员运动 1 至最高点，速度为零，之后运动员开始向下做匀加速直线运动，直至t 时刻开始减速，因此运动员在t 时刻入 2 2 水，故A错误。 B.运动员在t 时刻入水，故B错误 2 C.假设运动员的起跳速度大小为v ，从图像可知，运动员起跳至最高点的运动时间为t ， 0 1 从最高点下落至入水的运动时间为（t ﹣t ）＝1.5t ，入水时的速度大小为1.5v ， 2 1 1 0 1.5v v 综合上式，由题意可知 0 1.5t − 0 t ＝1m， 1 1 2 2 v 运动员起跳后上升的高度为h= 0 t ＝0.8m，故C正确。 1 2 D.因为运动员起跳后的上升过程为匀减速直线运动，初速度为 v ，末速度为0，因此有0−v2=−2gh，由此可得 0 0 v ＝4m/s，入水时的速度v＝1.5v ＝6m/s，故D错误。 0 0 故选：C。题型6利用图像分析加速度 14. （2024•重庆二模）某汽车沿直线停车过程中，其v﹣t图像如图所示。已知该汽车所有减速过程的加 速度均相等，中间有一段时间匀速运动，图示整个过程中该汽车行驶了450m。则该汽车匀速运动的时间为（ ） A．8s B．10s C．12s D．16.5s 20−5 【解析】v﹣t图像中斜率表示加速度大小，第一个减速阶段中可知a= m/s2＝0.5m/s2 30 5 5 第二次减速需要的时间为t= = s＝10s a 0.5 设匀速阶段结束的时间为t' 5+20 1 v﹣t图像面积为位移情况，所以450m= ×30m+5×（t'﹣30）m+ ×5×10m 2 2 解得t'＝40s 所以匀速阶段的时间为40s﹣30s＝10s，故B正确，ABD错误； 故选：B。 15. （2024•深圳校级模拟）雨雪天气时路面湿滑，与干燥路面相比，汽车在湿滑路面上刹车时的刹车距 离将明显增大。某驾驶员驾驶同一辆汽车在这两种路面上刹车过程中的 v﹣t图像如图所示。对这两种刹车过 程，下列说法正确的是（ ） A．图线a是汽车在湿滑路面刹车过程中的v﹣t图像 B．两种刹车过程中汽车的平均速度相同 C．汽车在湿滑路面上刹车时的加速度较大 D．汽车在两种路面上刹车时的位移大小与加速度大小成正比 【解析】AC、在其他条件相同的情况下，汽车在湿滑路面紧急刹车过程中的加速度较小，刹车距离较大，由图可知，图线b是汽车在湿滑路面紧急刹车过程中的v﹣t图线，故AC错误； v +v B、因为汽车在两过程中均做匀变速直线运动，且初速度和末速度均相同，所以根据公式v= 0 分析可知， 2 汽车在两种刹车过程中的平均速度相同，故B正确； D、汽车做匀减速直线运动，由v2=2ax知汽车在两种路面上刹车时的位移大小与加速度大小成反比，故D错误。 0 故选：B。 16. （2024•宁波模拟）某同学用v﹣t图像研究无人机在竖直方向的运动情况，如图所示。图像中只有 ab 段和cd段为直线，其直线方程分别是v ＝3t﹣2，v ＝10﹣2t。下列分析正确的是（ ） 1 2 A．无人机在ab段一定向上加速，在cd段一定向上减速 B．无人机在ab段和cd段的加速度方向相同 C．无人机在bc段的加速度变化量为﹣5m/s2 D．无人机在bc段的速度变化量为12m/s 【解析】A、由于题目中没有规定正方向，如果规定向上为正方向，则在ab段向上加速，在cd段向上减速运动； 如果规定向下为正方向，则在ab段向下加速，在cd段向下减速运动，故A错误； B、在v﹣t图像中，图像的斜率表示加速度，由图可知无人机在ab段和cd段的加速度方向相反，故B错误； C、根据v＝v +at可知在ab段的加速度为3m/s2，在cd段的加速度为﹣2m/s2， 0 因此在bc段的加速度变化量为Δa＝﹣2m/s2﹣3m/s2＝﹣5m/s2 故C正确； D、由于v﹣t图中没有具体数据，所以从图中数据无法确定无人机在bc段的速度变化量，故D错误。 故选：C。 17. （2024•琼山区校级模拟）甲、乙两物体做匀加速直线运动，速度﹣时间图象如图所示，则下列说法 正确的是（ ） A．两物体在相同的时间内运动的位移相同B．两物体的距离随时间均匀增大 C．乙观察到甲沿正方向做匀加速直线运动 D．在相同的时间内甲物体速度的增加量大于乙物体速度的增加量 【解析】A、图象与时间轴围成的面积表示物体的位移，由图可知甲的位移大于乙的位移，故A错误； B、由图可知，两图象之间的面积差值为两图之间的平行四边形，故随时间面积均匀增大，位移均匀增大，故B 正确； C、由于两人加速度相同，故两人相对为匀速直线运动，故C错误； D、因两人的加速度相同，故两人速度的增加量相同，故D错误； 故选：B。 18. （2024•青羊区校级模拟）在2023年10月3日举办的杭州亚运会上，中国运动员全红婵在10m跳台 跳水决赛中获得冠军，如图所示为她离开跳台后运动过程的简化v﹣t图像。下列说法正确的是（ ） A．在0～t 时间内她的加速度不变 2 B．裁判员给她打分时可以将她视为质点 C．她在水中的加速度逐渐增大 D．t 时刻她运动到最高点 2 【解析】AC、根据v﹣t图像的斜率表示加速度，可知在0～t 时间内，她的加速度保持不变，这个过程是在空 2 中运动，而在t 时刻进入水中后，加速度逐渐减小，故A正确，C错误； 2 B、裁判员给她打分时，要观察她的空中动作，所以不能将她视为质点，故B错误； D、从图像可知，在0～t 全红婵做竖直上抛运动，t 时刻她到达最高点，然后做自由落体运动，在t 时刻入水， 1 1 2 故D错误。 故选：A。第 2 讲 匀变速直线运动规律的应用 1、掌握并会利用匀变速直线运动规律处理物理问题。 2、掌握并会利用匀变速直线运动的推论处理物理问题 考点一 匀变速直线运动公式的应用 1．基本规律 (1)速度公式： v ＝ v ＋ a t. 0(2)位移公式：x＝vt＋at2. 0 (3)位移速度关系式： v 2 － v ＝ 2 ax . 这三个基本公式，是解决匀变速直线运动的基石．均为矢量式，应用时应规定正方向． 2．两个重要推论 (1)物体在一段时间内的平均速度等于这段时间中间时刻的瞬时速度，还等于初、末时刻速度矢量和的一半，即： ＝v ＝. (2)任意两个连续相等的时间间隔T内的位移之差为一恒量，即：Δx＝x－x＝x－x＝…＝x－x ＝ aT 2 . 2 1 3 2 n n－1 3．v＝0的四个重要推论 0 (1)1T末、2T末、3T末、……瞬时速度的比为：v∶v∶v∶…∶v＝ 1∶2∶3∶…∶ n 1 2 3 n (2)1T内、2T内、3T内……位移的比为：x∶x∶x∶…∶x＝ 1 2 ∶2 2 ∶3 2 ∶…∶ n 2 1 2 3 n (3)第一个T内、第二个T内、第三个T内……位移的比为：x∶x ∶x ∶…∶x＝ 1∶3∶5∶…∶(2 n － 1) Ⅰ Ⅱ Ⅲ n (4)从静止开始通过连续相等的位移所用时间的比为： t∶t∶t∶…∶t＝1∶(－1)∶(－)∶…∶(－) 1 2 3 n [例题1] （2024•佛山一模）为提高航母的效能，福建舰安装了电磁弹射器，舰载机在弹射器的助推下能 获得30m/s2～50m/s2的加速度。若某舰载机从静止开始弹射，匀加速运动 150m达到100m/s的起飞速度，则 该过程的时间为（ ） A．3.3s B．3.0s C．2.5s D．1.5s x v 【解答】解：由题意可知，舰载机从静止开始弹射，匀加速运动150m达到100m/s的起飞速度，则根据 = t 2 代入数据解得 t＝3.0s，故B正确。 故选：B。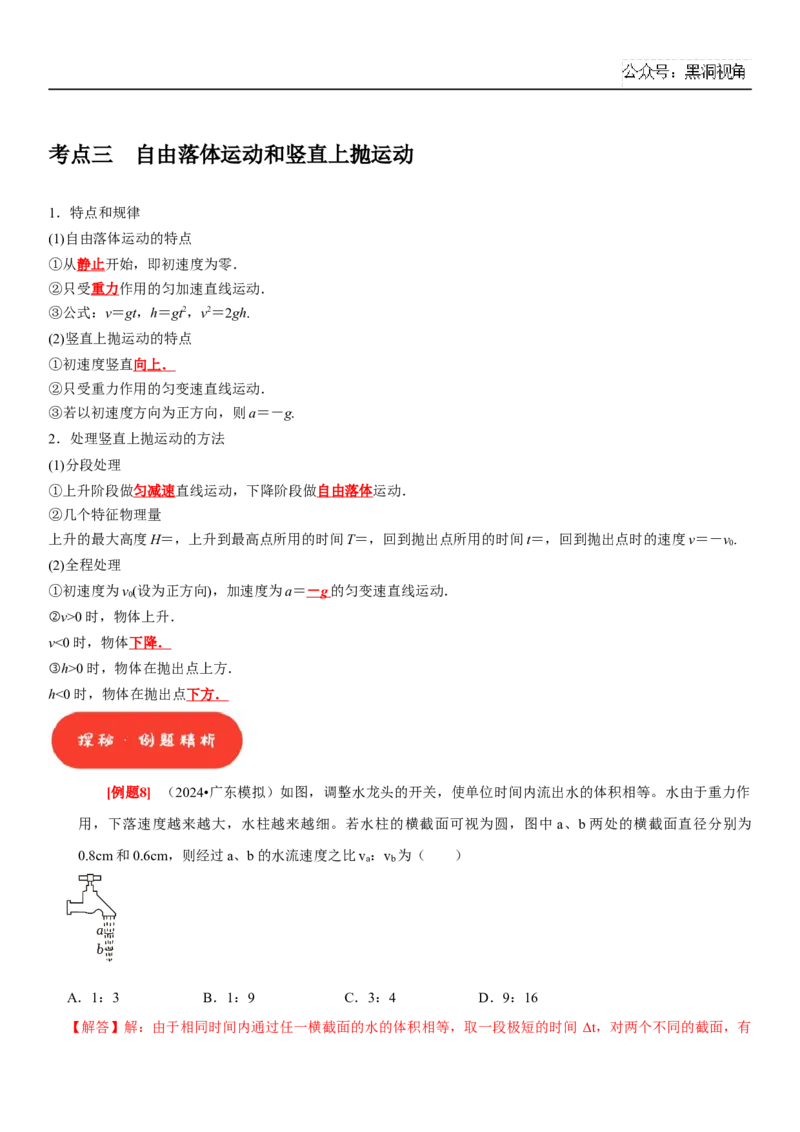 [例题2] （多选）（2022•庐阳区校级模拟）物理学中有一些经典实验通过巧妙的设计使用简陋的器材反 映了深刻的物理本质，例如伽利略的斜面实验就揭示了匀变速直线运动的规律。某同学用现代实验器材改进 伽利略的经典斜面实验，如图1所示，他让小球以某﹣﹣确定的初速度从固定斜面顶端0点滚下，经过A、B 两个传感器，其中B传感器固定在斜面底端，利用传感器测出了A、B间的距离x及小球在A、B间运动的时 间t。改变A传感器的位置，多次重复实验，计算机作出图像如图2所示。下列说法正确的是（ ）A．小球在斜面上运动的平均速度大小为8m/s B．小球在斜面上0点的速度大小为4m/s C．小球在斜面上运动的加速度大小为2m/s2 D．固定斜面的长度为6m 【解答】解：设小球在经过A传感器时的速度大小为v ，在斜面上运动的加速度大小为a，根据运动学规律可 A 得v ＝v +at B A 1 x=v t+ at2 A 2 x 1 a 联立并化简得： =v ⋅ − t2 B t 2 结合图像可得：v ＝8m/s；a＝4m/s2 B 1 当A传感器放置在O点时，传感器所测时间为小球从O到B传感器的运动时间t ，对应图像上 的最小值，即 1 t 1 =1s−1 t 1 解得：t ＝1s 1 所以小球在斜面上O点的速度大小为 v ＝v ﹣at ＝8m/s﹣4×1m/s＝4m/s 0 B 1 小球在斜面上运动的平均速度大小为 v +v 4+8 v= 0 B= m/s=6m/s 2 2 固定斜面长度为l=vt =6×1m=6m，故AC错误，BD正确； 1 故选：BD。 [例题3] （2024•新郑市校级三模）一质点在连续的6s内做匀加速直线运动，在第一个 2s内位移为 12m，最后一个2s内位移为36m，下面说法正确的是（ ） A．质点的加速度大小是6m/s2B．质点的加速度大小是3m/s2 C．质点第2s末的速度大小是12m/s D．质点在第1s内的位移大小是6m 【解答】解：AB、设第一个 2s 内的位移为 x ，第三个 2s 内，即最后 1 个 2s 内的位移为 x ，根据 1 3 x −x =2aT2，可得加速度a＝3m/s2，故A错误，B正确； 3 1 C、由匀变速直线运动连续相等时间内通过的位移差为定值，即x ﹣x ＝x ﹣x ，解得x ＝24m，第2s末的瞬时 3 2 2 1 2 x +x 速度等于前4s内的平均速度，则第2s末速度为v= 2 1，解得v＝9m/s，故C错误； 2T x 36 D、第1 s末的瞬时速度等于第一个2s内的平均速度，则v = 1= m/s＝6m/s，在第1 s内反向看为匀减速运动 1 T 6 1 则有x ＝v t− at2，解得x ＝4.5m，故D错误。 1 1 2 1 故选：B。 考点二 常用的“六种”物理思想方法 1．一般公式法 一般公式法指速度公式、位移公式及推论三式．它们均是矢量式，使用时要注意方向性． 2．平均速度法 定义式＝对任何性质的运动都适用，而 ＝ v ＝ ( v ＋ v )只适用于匀变速直线运动． 0 3．比例法 对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动，可利用初速度为零的匀加速直线运动的重要 特征中的比例关系，用比例法求解． 4．逆向思维法 如匀减速直线运动可视为反方向的匀加速直线运动． 5．推论法 利用Δx＝aT2：其推广式x －x＝ ( m － n ) aT2，对于纸带类问题用这种方法尤为快捷． m n 6．图象法 利用v－t图可以求出某段时间内位移的大小，可以比较v 与v ，还可以求解追及问题；用x－t图象可求出任意 时间内的平均速度等．[例题4] （2024•湖北二模）如图所示，在2022年北京冬奥会高山滑雪男子大回转比赛中，中国选手张洋 铭沿着雪道加速滑下，途经a、b、c、d四个位置。若将此过程视为匀加速直线运动，张洋铭在ab、bc、cd三 段位移内速度增加量之比为1：2：1，a、b之间的距离为L ，c、d之间的距离为L ，则b、c之间的距离L 1 3 2 为（ ） 8 A．8L B． L 1 7 3 1 C．L +L D． (L +L ) 1 3 2 1 3 【解答】解：张洋铭在ab、bc、cd三段位移内速度增加量之比为1：2：1，则对应时间之比为1：2：1，有 1 L =v t+ at2 1 0 2 1 L ＝（v +at）•2t+ a（2t）2＝2v t+4at2 2 0 2 0 1 7 L ＝（v +3at）•t+ at2＝v t+ at2 3 0 2 0 2 根据数学知识观察可得 L ＝L +L 2 1 3 故ABD错误，C正确。 故选：C。 [例题5] （2024•琼山区校级模拟）沿平直轨道匀加速行驶的长度为L的列车，保持加速度不变通过长度 为L的桥梁，车头驶上桥头时的速度为 v ，车头经过桥尾时的速度为 v ，则车尾通过桥尾时的速度为 1 2 （ ） A．v ：v B．√2v 2−v 2 1 2 2 1 C．√v 2+v 2 D．√2v 2+v 2 1 2 2 1 【解答】解：火车车头从桥头到桥尾运动的过程中，根据速度—位移关系可得：2aL＝v 2﹣v 2 2 1 火车车头从桥头到车尾通过桥尾的过程中，根据速度—位移关系可得：2a•2L＝v2﹣v 2 1 解得：v=√2v 2−v 2，故B正确、ACD错误。 2 1故选：B。 [例题6] （2024•日照一模）某物理学习兴趣小组研究公交车的运动，公交车进站过程认为做匀减速直线 运动直至停下。公交车在最初6s内通过的位移与最后6s内通过的位移之比为21：9，若公交车运动的加速度 大小为1m/s2，则（ ） A．公交车运动的总位移为60m B．公交车在最初6s内通过的位移与最后6s内通过的位移之差为36m C．公交车的初速度为12m/s D．公交车运动的时间为10s 【解答】解：设公交车开始减速的速度为 v ，运动总时间为 t，则公交车在最初减速 6s内通过的位移为 0 1 x =v t − at2=(6v −18m) 1 0 0 2 0 0 1 把物体运动看成反向的初速度为0的匀加速直线运动，最后6s内通过的位移为x = at2 2 2 1 代入数据解得x ＝18m 2 由于公交车在最初6s内通过的位移与最后6s内通过的位移之比为21：9，则由以上有 6v −18 21 0 = 18 9 又有0＝v ﹣at 0 代入数据解得v ＝10m/s 0 t＝10s 1 则公交车的总位移为x=v t− at2 0 2 代入数据解得x＝50m 公交车在最初6s内通过的位移与最后6s内通过的位移之差为Δx＝x ﹣x 1 2 代入数据解得 Δx＝24m，故ABC错误，D正确。 故选：D。 [例题7] （2024•长沙模拟）2023年8月28日株洲清水塘大桥正式通车。如图甲所示，大桥全长 2.85千 米，主跨为408米双层钢桁架拱桥结构，位列同类桥梁中湖南第一、桥梁上层为机动车道，下层为行人和非 机动车通行的景观通道。大桥一经开通就成为了株洲市民观光散步、娱乐休闲的“网红桥”。图乙中 A、B、 C、D、E、F为大桥上的六根竖直钢丝绳吊索，相邻两根吊索之间距离均相等，若一汽车在桥梁上层从吊索A 处开始做匀减速直线运动，刚好在吊索E、F的中点N点停下，汽车通过吊索E时的瞬时速度为v ，从E点 E 到N点的时间为t，则（ ）A．汽车通过吊索A时的速度为9v E B．汽车通过AE段的时间等于3t C．汽车通过AE段的平均速度是EN段平均速度的4倍 D．汽车通过全程AN的平均速度小于v E 【解答】解：A．令加速度为a，E到N的距离为L，从E到N有 v2=2aL E 从N到A有 v2 =2a⋅9L A 联立可得 v ＝3v A E 故A错误； B．根据速度—时间公式，有 v −v 2v t = A E= E AE a a v −0 v t = E = E=t EN a a 所以汽车通过 AE 段的时间等于2t，故B错误； C．根据匀变速直线运动的推论有 v +v v = A E=2v AE 2 E v +0 v v = E = E EN 2 2 所以汽车通过 AE段的平均速度是EN段平均速度的4倍，故C正确； D．根据平均速度与瞬时速度的关系可知，汽车通过全程AN的平均速度为 v +0 3v v = A = E＞v AN 2 2 E 故D错误。 故选：C。考点三 自由落体运动和竖直上抛运动 1．特点和规律 (1)自由落体运动的特点 ①从静止开始，即初速度为零． ②只受重力作用的匀加速直线运动． ③公式：v＝gt，h＝gt2，v2＝2gh. (2)竖直上抛运动的特点 ①初速度竖直向上． ②只受重力作用的匀变速直线运动． ③若以初速度方向为正方向，则a＝－g. 2．处理竖直上抛运动的方法 (1)分段处理 ①上升阶段做匀减速直线运动，下降阶段做自由落体运动． ②几个特征物理量 上升的最大高度H＝，上升到最高点所用的时间T＝，回到抛出点所用的时间t＝，回到抛出点时的速度v＝－v. 0 (2)全程处理 ①初速度为v(设为正方向)，加速度为a＝ － g 的匀变速直线运动． 0 ②v>0时，物体上升． v<0时，物体下降． ③h>0时，物体在抛出点上方． h<0时，物体在抛出点下方． [例题8] （2024•广东模拟）如图，调整水龙头的开关，使单位时间内流出水的体积相等。水由于重力作 用，下落速度越来越大，水柱越来越细。若水柱的横截面可视为圆，图中 a、b两处的横截面直径分别为 0.8cm和0.6cm，则经过a、b的水流速度之比v ：v 为（ ） a b A．1：3 B．1：9 C．3：4 D．9：16 【解答】解：由于相同时间内通过任一横截面的水的体积相等，取一段极短的时间 Δt，对两个不同的截面，有d d π( a ) 2v Δt=π( b ) 2v Δt 2 a 2 b 可得v ：v =d2：d2=0.62：0.82=9：16 a b b a 故ABC错误，D正确。 故选：D。 [例题9] （2024•琼山区校级模拟）2012年6月1日，空降兵某部官兵使用新装备从260m超低空跳伞成 功．若跳伞空降兵在离地面224m高处，由静止开始在竖直方向做自由落体运动．一段时间后，立即打开降落 伞，以12.5m/s2的平均加速度匀减速下降，为了空降兵的安全，要求空降兵落地速度最大不得超过5m/s（g取 10m/s2）．则（ ） A．空降兵展开伞时离地面高度至少为125 m，相当于从2.5 m高处自由落下 B．空降兵展开伞时离地面高度至少为125 m，相当于从1.25 m高处自由落下 C．空降兵展开伞时离地面高度至少为99 m，相当于从1.25 m高处自由落下 D．空降兵展开伞时离地面高度至少为99 m，相当于从2.5 m高处自由落下 【解答】解：设空降兵做自由落体运动的高度为h时速度为v，此时打开伞开始匀减速运动，落地时速度刚好 为5m/s，这种情况空降兵在空中运动时间最短，则有v2＝2gh，v2﹣v2＝2a（H﹣h） t 解得：h＝125m，v＝50m/s，为使空降兵安全着地，他展开伞时的高度至少为 H﹣h＝224m﹣125m＝99m，故 A、B错误； v2 25 他以5m/s的速度着地时，相当于从h′高处自由落下，由v2＝2gh′，得h′= t = m＝1.25m，选项D错误， t 2g 2×10 C正确。 故选：C。 [例题10]（2024•开福区校级模拟）在地面上以初速度2v 竖直上抛一物体A后，又以初速度v 从同一地 0 0 点竖直上抛另一物体B。若要使两物体能在B上升过程中相遇，则两物体抛出的时间间隔Δt必须满足的条件 是（不计空气阻力，重力加速度大小为g）（ ） 2v 3v 2v 4v A． 0＜Δt＜ 0 B． 0＜Δt＜ 0 g g g g (√3+1)v 4v 3v 4v C． 0＜Δt＜ 0 D． 0＜Δt＜ 0 g g g g 【解答】解：设B经过时间t，AB在空中相遇，有： 1 1 2v (t+Δt)− g(t+Δt) 2=v t− gt2 0 2 0 2 v 上升过程中相遇：0＜t＜ 0 g(√3+1)v 4v 解得： 0＜Δt＜ 0。 g g 故C正确，ABD错误。 故选：C。 [例题11] （2024•皇姑区校级模拟）如图所示，A，B两棒的长度相同，A的下端和B的上端相距s＝ 40m。若A，B同时运动，A做自由落体运动，B做竖直上抛运动且初速度v ＝20m/s（g取10m/s2），则A， 0 B相遇时A的速度大小为（ ） A．40m/s B．10m/s C．30m/s D．20m/s 1 【解答】解：根据位移—时间公式，可得A棒自由落体运动位移为：x = gt2 1 2 1 B棒做竖直上抛运动位移为：x ＝v t− gt2 2 0 2 二者的位移关系：x +x ＝s 1 2 联立并代入数据解得A，B两棒相遇的时间为：t＝2s 根据速度—时间公式，可得A，B相遇时A的速度大小为： v ＝gt＝10×2m/s＝20m/s，故D正确，ABC错误。 A 故选：D。 题型1匀变速直线运动基本公式的应用 1. （2023秋•叙州区校级期末）一物体车以﹣5m/s2做匀变速直线运动，那么下列关于该物体运动的描 述正确的是（ ） A．该物体在做匀减速直线运动 B．下一秒末与前一秒初的速度变化量大小为5m/s C．下一秒末与前一秒末的速度变化量大小为5m/s D．下一秒的平均速度比前一秒的平均速度小5m/s【解答】解：A、不知初速度方向，从而不能确定物体做加速还是减速运动，故A错误； B、下一秒末与前一秒初的时间间隔为2s，则Δv＝at＝5×2m/s＝10m/s，故B错误； C、下一秒末与前一秒末的时间间隔为1s，则Δv＝at＝5×1m/s＝5m/s，故C正确； D、下一秒比前一秒多1s，则故两段时间的中间时刻也相差1s，故平均速度相差v＝at＝5×1m/s＝5m/s，由于不 知是加速还是减速，故下一秒的平均速度比前一秒的平均速度可能小5m/s，也可能大5m/s，故D错误； 故选：C。 2. （2024•北京模拟）一质点静止在光滑水平面上，先向右做初速度为零的匀加速直线运动，加速度大 小为a ，经过时间t后加速度变为零；又运动时间t后，质点加速度方向变为向左，且大小为a ，再经过时间 1 2 t后质点回到出发点。以出发时刻为计时零点，则在这一过程中（ ） A．a ＝3a 2 1 8 B．质点向右运动的最大位移为 a t2 5 2 4 C．质点回到出发点时的速度大小为 a t 5 2 D．最后一个时间t内，质点的位移大小和路程之比为3：5 【解答】解：A、以向右为正方向，由速度—时间公式有：v ＝a t 1 1 由题意三段时间返回出发点可列：0＝x +x +x 1 2 3 1 1 由位移—时间公式得：x = a t2 ，x ＝v t，x =v t− a t2 1 2 1 2 1 3 1 2 2 代入解得：a ＝5a ，故A错误； 2 1 B、根据题意，作出质点运动的v﹣t图象，如图所示， 设向右从v 减速到0所用的时间为t′，则有：v ＝a t′ 1 1 2 又因为：v ＝a t 1 1 1 解得：t'= t 5 1 1 根据v﹣t图象的面积表示位移大小可知，质点向右运动的最大位移：x= v t+v t+ v ⋅t'，代入数据得：x 2 1 1 2 1 8 = a t2，故B错误； 5 11 4 4 C、质点回到出发点时所用的时间为：t″＝t﹣t′＝t− t= t，则对应的速度大小为：v ＝a t″= a t，故C正确； 5 5 2 2 5 2 3 D、最后一个时间t内，质点的位移大小为：x′＝x +x ，代入数据得：x′= a t2 1 2 2 1 1 1 1 4 17 路程：s= a t× t+ ×4a t× t，代入数据得：s= a t2 2 1 5 2 1 5 10 1 所以最后一个时间t内，质点的位移大小和路程之比为15：17，故D错误。 故选：C。 3. （2024•琼山区校级模拟）一步行者以6.0m/s的速度跑去追赶被红灯阻停的公交车，在跑到距汽车 25m处时，绿灯亮了，汽车以1.0m/s2的加速度匀加速启动前进，则（ ） A．人不能追上公共汽车，且车开动后，人车距离越来越远 B．人不能追上公共汽车，人、车最近距离为7m C．人能追上公共汽车，追赶过程中人跑了36m D．人能追上公共汽车，追上车前人共跑了43m v 6 【解答】解：当两车速度相等时，经历的时间t= = s=6s．此时人的位移x ＝vt＝6×6m＝36m，汽车的位移 a 1 1 1 1 x = at2= ×1×36m=18m。 2 2 2 因为x ＜x +25m，可知人不能追上汽车。 1 2 速度相等时有最小距离，最小距离Δx＝x +25﹣x ＝18+25﹣36m＝7m。 2 1 在追及的整个过程中，人车距离先减小再增大。故B正确，A、C、D错误。 故选：B。 题型2刹车类问题 4. （2023秋•宁波期末）2023年SUV制动距离排行榜上国产汽车成绩进步明显，如图中吉利车型领克 05测试过程中以100km/h的初速度进行刹车制动，经过34m的距离刹停。若制动过程可看成匀减速直线运动， 关于此次测试过程，该车（ ）A．刹车时间约为2.4s B．刹车过程的加速度大小约为147m/s2 C．刹车过程的平均速度大小为50m/s D．在第3s末的速度大小约为6m/s 【解答】解：初速度大小为v ＝100km/h≈27.8m/s。 0 v A、设刹车时间约为t，则有： 0t=x，解得：t＝2.4s，故A正确； 2 v 27.8 B、根据加速度的定义式可得：a≈ 0= m/s2=11.6m/s2，故B错误； t 2.4 v 27.8 C、刹车过程的平均速度大小为v= 0= m/s＝13.9m/s，故C错误； 2 2 D、由于刹车时间约为2.4s，所以在第3s末的速度大小为0，故D错误。 故选：A。 5. （2023秋•海安市期末）神舟十六号载人飞船返回地面，速度为 v 时开启缓冲发动机，获得大小为a 0 的加速度，经过时间t后速度恰好为零，则该过程中飞船的位移可以表达为（ ） 1 v t A．v t+ at2 B． 0 0 2 2 a2 t C． D． 2v 2v 0 0 1 【解答】解：由题意可知，飞船做匀减速直线运动，由位移公式可得其该时间内的位移为：x=v t− at2 ； 0 2 v +0 v 又由匀变速直线运动的平均速度与位移的关系可得该阶段内的位移为x=vt= 0 t= 0t； 2 2 v2 由匀变速直线运动的速度—位移公式可得：v2=2ax，可得x= 0 ，故B正确，ACD错误。 0 2a 故选：B。 6. 冰壶（Crling），又称掷冰壶、冰上溜石，是以队为单位在冰上进行的一种投掷性竞赛项目，属冬奥 会比赛项目，并设有冰壶世锦赛。中国女子冰壶队于2003年成立，在2009年的女子冰壶世锦赛上战胜诸多劲旅夺冠，已成长为冰壶领域的新生力军。在某次比赛中，冰壶被投出后，如果做匀减速直线运动用时 20s 停止，最后1s内的位移大小为0.2m，则下列说法正确的是（ ） A．冰壶的加速度大小是0.3m/s2 B．冰壶第1s内的位移大小是78m C．全程的平均速度大小为4m/s D．冰壶的初速度大小是6m/s 【解答】解：A、冰壶的运动为末速度为0的匀减速直线运动，可逆向看作初速度为0的匀加速直线运动，设冰 1 壶的加速度大小为a，根据位移—时间公式得：x = at2 1 2 1 代入数据解得：a＝0.4m/s2 故A错误； D、冰壶的初速度v ＝at＝0.4×20m/s＝8m/s 0 故D错误； 1 1 B、冰壶第1s内的位移大小是x ＝v t − at2=8×1m/s− ×0.4×12m＝7.8m 2 01 2 1 2 故B错误； v 8 C、全程的平均速度大小为v= 0= m/s＝4m/s 2 2 故C正确； 故选：C。 题型3匀变速直线运动中的多过程问题 7. （2024•延边州一模）如图，某滑雪爱好者从倾角一定的雪道上A点由静止滑下，滑到水平雪道上C 点时速度刚好为零，滑雪爱好者经过倾斜雪道的最低点B点时速度大小不变。若滑雪爱好者在倾斜和水平雪 道上均做匀变速直线运动，已知从A到C运动的路程为60m，时间为40s，则该滑雪爱好者经过B点时的速 度大小为（ ） A．5m/s B．3m/s C．4m/s D．2m/s 【解答】解：设滑雪爱好者经过B点时的速度大小为v，在AB段运动时间为t ，路程为x ，BC段运动时间为 1 1t ，路程为x ，根据匀变速直线运动的规律有 2 2 v x = •t 1 2 1 v x = •t 2 2 2 且t +t ＝40s 1 2 x +x ＝60m 1 2 联立解得 v＝3m/s 故ACD错误，B正确； 故选：B。 8. （2024•渝中区模拟）汽车已经走进了千家万户，成为普通家庭的消费品，驾驶技能从职业技能成为 基本生活技能。考驾照需要进行一项路考——定点停车。路旁竖一标志杆，在车以大小为 v的速度匀速行驶 的过程中，当车头与标志杆的距离为x时，学员立即刹车，让车做匀减速直线运动，车头恰好停在标志杆处。 若忽略学员的反应时间，则汽车刹车（ ） x A．时间为 v v2 B．加速度大小为 2x x C．经过一半时间时的位移大小为 2 v D．经过一半距离时的速度大小为 2 【解答】解：根据逆向思维法，将匀减速直线运动反向处理成初速度为0的匀加速直线运动。 v 2x A.根据匀变速直线运动位移—时间规律有x= •t，得t= ，故A错误； 2 v v2 v2 B.根据匀变速直线运动位移—速度规律有x= ，得a= ，故B正确； 2a 2x C.根据初速度为0的匀加速直线运动规律，把总时间平分，则位移之比为1：3，故按原题经过一半时间对应的 3 位移为总位移的 x，故C错误； 4 √0+v2 √2 D.根据初速度为0的匀加速直线运动规律，把总位移平分，由公式v′= = v，故D错误。 2 2 故选：B。 9. （2023秋•福田区校级期末）某次列车出站时做匀加速运动，途中连续经过三个测试点 A、B、C，已知AB段距离为BC段的一半，AB段平均速度为72km/h，BC段平均速度为144km/h，如图所示，则列车经 过C点时速度大小为（ ） A．30m/s B．40m/s C．50m/s D．60m/s 【解答】解：设AB段距离为x，BC段距离为2x，AB段平均速度为v ＝72km/h＝20m/s 1 BC段平均速度为v ＝144km/h＝40m/s 2 可知v ＝2v 2 1 x 由于AB段距离为BC段的一半，根据：t= ，可得列车经过AB段和BC段的时间相等。 t 设列车经过AB段和BC段的时间均为t，根据匀变速直线运动的平均速度等于中间时刻的瞬时速度的性质，可 x +x v t+v t v +v 20+40 得列车经过B点时速度等于AC段的平均速度，则有v = AB BC = 1 2 = 1 2= m/s＝30m/s B 2t 2t 2 2 v +v 由匀变速直线运动的规律可得v = B C 2 2 解得列车经过C点时速度大小为v ＝50m/s，故ABD错误，C正确。 C 故选：C。 题型4平均速度和中点时刻瞬时速度 10. （2023秋•玉溪期末）一质点做匀加速直线运动，依次通过a、b、c三点。测得a、b两点之间的距离 为s，b、c两点之间的距离为4s，通过ab段所用时间为t，通过bc段所用时间为2t。则该质点运动的加速度 大小为（ ） s s s 2s A． B． C． D． 4t2 2t2 t2 3t2 【解答】解：ab段中间时刻的速度大小为 s v = 1 t bc段中间时刻的速度大小为 4s v = 2 2t 从ab段中间时刻到bc段中间时刻经历的时间t Δt= +t 2 可得 v ﹣v ＝aΔt 2 1 解得 2s a= 3t2 故D正确，ABC错误。 故选：D。 11. （2023秋•杭州期中）运动会上，用电子机器狗运送铁饼既便捷又安全，将机器狗在某次运送铁饼的 运动过程视为匀加速直线运动，相继经过两段距离为12米的路程，用时分别为6s和4s。则机器狗的加速度 大小是（ ） A．0.1m/s2 B．0.2m/s2 C．0.48m/s2 D．2m/s2 Δx 12 Δx 12 【解答】解：第一段的平均速度为：v = = m/s＝2m/s，第二段的平均速度为v = = m/s＝3m/s，根 1 Δt 6 2 Δt 4 据某段时间内的平均速度等于中间时刻的瞬时速度知，两个中间时刻的时间间隔为 Δv 3−2 Δt＝（3+2）s＝5s，则加速度为a= = m/s2＝0.2m/s2。 Δt 5 故选：B。 题型5中间位置瞬时速度 12. （2023秋•雨花区校级月考）如图所示是某物体做直线运动的v2﹣x图像（其中v为速度，x为位置 坐标），下列关于物体从x＝0处运动至x＝x 处的过程分析，正确的是（ ） 0A．该物体做匀加速直线运动 v2 B．该物体的加速度大小为 0 2x 0 1 C．该物体在位移中点的速度小于 v 2 0 1 D．该物体在运动中间时刻的速度大于 v 2 0 【解答】解：A、由匀变速直线运动的速度—位移关系公式v2−v2=2ax，可得v2＝2ax+v2，可知物体的加速度 0 0 恒定不变，速度均匀减小，故物体做匀减速直线运动，故A错误； v2 v2 B、由上式知，v2﹣x图象的斜率等于2a，由图可得：2a= 0，则物体的加速度大小为a= 0 ，故B正确； x 2x 0 0 v +v CD、设匀变速运动的初速度为v ，末速度为v，中间时刻的瞬时速度等于平均速度，即v = 0 ，中点位移 0 t 2 2 √v2+v2 v v v2+2v v+v2 v2+v2 (v −v) 2 v ＜v 速度为v = 0 ，则：（ t）2﹣（ x）2= 0 0 − 0 =− 0 ＜0，故 t x，即物体 x 2 2 2 4 2 4 2 2 2 在中间时刻的瞬时速度小于在位移中点的速度。 v 该物体在运动过程中的平均速度为 0，因为物体做匀减速直线运动，所以该物体在运动中间时刻的速度等于平 2 v v 均速度 0，而物体在位移中点的速度大于中间时刻的速度，所以物体在位移中点的速度大于 0，故CD错误。 2 2 故选：B。 v 13. 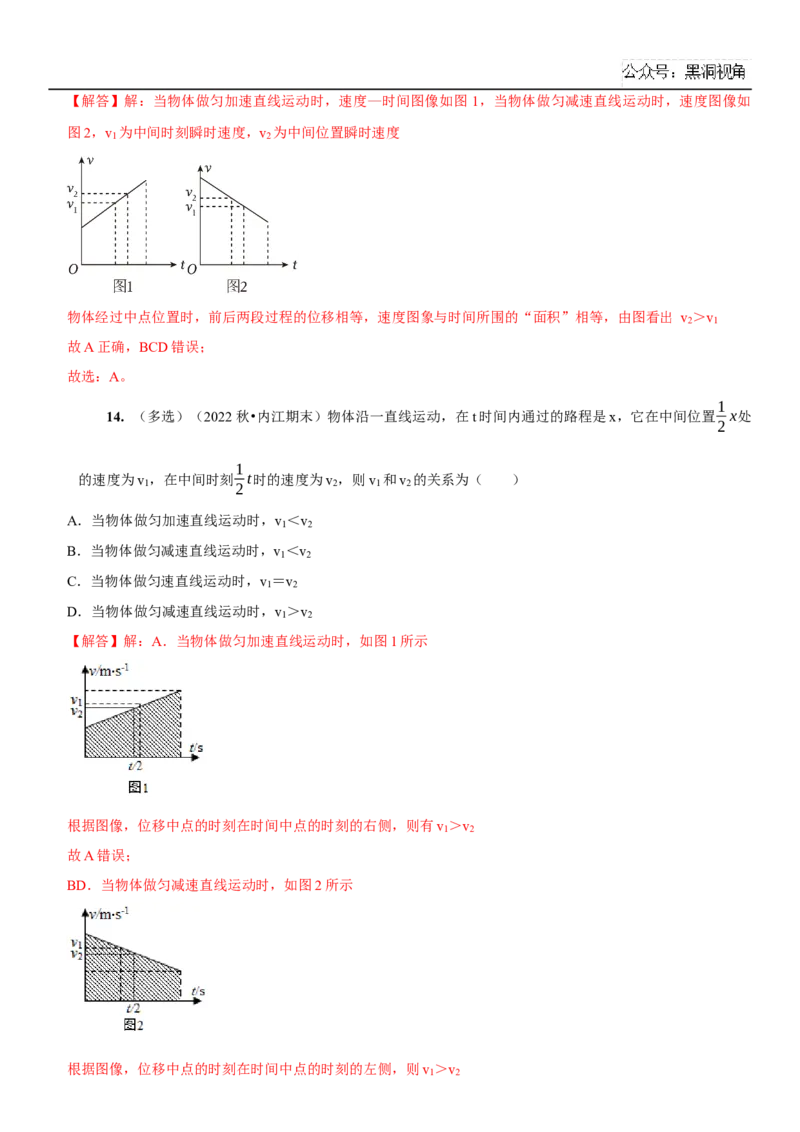（2023秋•越秀区校级月考）在匀变速直线运动中，关于中间时刻瞬时速度的大小 t和中间位置瞬时 2 v 速度的大小 s，下列说法正确的是（ ） 2 v ＞v A．不论物体是做匀加速直线运动还是做匀减速直线运动，总有 s t 2 2 v ＞v B．只有做匀加速直线运动时有 s t 2 2 v ＞v C．只有做匀减速直线运动时有 s t 2 2 D．以上说法都不对【解答】解：当物体做匀加速直线运动时，速度—时间图像如图 1，当物体做匀减速直线运动时，速度图像如 图2，v 为中间时刻瞬时速度，v 为中间位置瞬时速度 1 2 物体经过中点位置时，前后两段过程的位移相等，速度图象与时间所围的“面积”相等，由图看出 v ＞v 2 1 故A正确，BCD错误； 故选：A。 1 14. （多选）（2022秋•内江期末）物体沿一直线运动，在t时间内通过的路程是x，它在中间位置 x处 2 1 的速度为v ，在中间时刻 t时的速度为v ，则v 和v 的关系为（ ） 1 2 2 1 2 A．当物体做匀加速直线运动时，v ＜v 1 2 B．当物体做匀减速直线运动时，v ＜v 1 2 C．当物体做匀速直线运动时，v ＝v 1 2 D．当物体做匀减速直线运动时，v ＞v 1 2 【解答】解：A．当物体做匀加速直线运动时，如图1所示 根据图像，位移中点的时刻在时间中点的时刻的右侧，则有v ＞v 1 2 故A错误； BD．当物体做匀减速直线运动时，如图2所示 根据图像，位移中点的时刻在时间中点的时刻的左侧，则v ＞v 1 2故B错误，D正确； C．当物体做匀速直线运动时，速度始终不变，故v ＝v 1 2 故C正确。 故选：CD。 题型6逐差法 15. （2022秋•孝感期末）物体从静止开始做匀加速直线运动，已知第4s内与第2s内的位移之差是8m。 则下列说法错误的是（ ） A．物体运动的加速度为8m/s2 B．第2s末的速度为8m/s C．第2s内的位移为6m D．物体在0～3s内的平均速度为6m/s 【解答】解：A、由 x −x =2aT2 4 2 可知，物体运动的加速度为 x −x 8 a= 4 2= m/s2=4m/s2 2T2 2×1 故A错误； B、由速度公式 v ＝at＝4×2m/s＝8m/s 2 故B正确； C、由 1 x= at2 2 可得 1 1 Δx = ×4×22m− ×4×12m=6m 2 2 2 故C正确； D、由平均速度定义 x v= t'可得 1 1 at'2 ×4×32 2 2 v= = m/s=6m/s t' 3 故D正确。 故选：A。 题型7初速度为零的匀加速直线运动的比例关系 16. （2024•荔湾区校级开学）如图所示，在水平面上固定着三个完全相同的木块，一颗子弹（可视为质 点），以水平速度v 射入，子弹可视为质点。若子弹在木块中做匀减速直线运动，当它穿透第三个木块（即 0 C位置）时速度恰好为0，下列说法正确的是（ ） A．子弹通过每个木块的时间均相同 B．子弹到达各点的速率之比为v ：v ：v =√3：√2：1 O A B C．子弹通过每一部分时，其速度变化量相同 D．子弹从O运动到C全过程的平均速度等于B点的瞬时速度 【解答】解：AC、根据逆向思维，子弹运动的逆过程是由C点开始做初速度为0的匀加速直线运动到O点的过 程 ， 根 据 初 速 度 为 零 的 匀 加 速 直 线 运 动 的 推 论 可 知 ： 连 续 相 等 位 移 所 用 时 间 之 比 为 ： 1：(√2−1)：(√3−√2)：(2−√3)...，可知子弹通过每个木块的时间均不相同。 根据Δv＝at，由于子弹通过每一部分所用时间不相等，则速度变化量不相同，故A错误，C错误； B 、 根 据 速 度 — 位 移 公 式 v2 ＝ 2ax ， 可 得 v=√2ax， 则 子 弹 到 达 各 点 的 速 率 之 比 为 ： v ：v ：v =√3：√2：1，故B正确； O A B D、根据匀变速直线运动中全过程的平均速度等于中间时刻的瞬时速度，可知子弹从 O点运动到C点全过程的 平均速度不等于B点的瞬时速度，故D错误。 故选：B。 17. （多选）（2023秋•大通县期末）滑块以某一初速度从斜面底端O上滑到最高点D，用频闪仪记录的 上滑过程如图所示，则（ ）A．滑块在B点的速度大小为在C点的两倍 B．滑块在A点的速度大小为在C点的两倍 C．AB和CD的距离之比为3：1 D．AB和CD的距离之比为5：1 【解答】解：AB、滑块从O到D做匀减速运动，可看成从D到O的初速度为零的匀加速直线运动，设频闪仪 记录的时间间隔为T，滑块的加速度为a，则 v ＝aT，v ＝2aT，v ＝3aT，故A正确，B错误； C B A CD、由初速度为零的匀加速直线运动推论知AB和CD的距离之比为5：1，故C错误，D正确； 故选：AD。 18. （2023秋•光明区校级期中）如图所示，九个相同的木块并排固定在水平面上，从左至右编号依次为 1、2、…、8、9。一个子弹（可视为质点）从木块1左端以速度v射入，恰好没有从木块9穿出，则下列说法 正确的是（ ） A．子弹刚进入木块6和刚进入木块9时的速度大小之比为2：1 B．子弹穿过前三个木块的时间和穿过后三个木块的时间之比为1：√4−√3 C．子弹刚进入木块9时的速度与初速度v的大小之比为1：√2 v D．子弹在木块5中点的速度大小为 2 【解答】解：AC、把子弹的运动看成逆向初速度为零的匀加速直线运动，由运动学公式： 1 x= at2 2 v＝at 联立得：v=√2ax 则：v ：v ＝2：1，故A正确； 6 9 则：v ：v ＝1：3，故C错误； 9 1 B、设子弹穿过前三个木块所需时间为t 、位移为x ，穿过后三个木块所需时间为t 、位移为x ，穿过后六个所 1 1 2 2 需时间为t 、位移为x ，运动全程所需时间为t 、位移为x ，由运动学公式得： 3 3 4 4 √2x t = 2 2 a√2x √2x t =t −t = 4− 3 1 4 3 a a 则：t ：t =(√3−√2)：1 1 2 故B错误； D、由中间位置速度公式： √v2+v2 v = 9 5.5 2 √2 得：v = v，故D错误。 5.5 2 故选：A。 题型8自由落体运动的基本规律应用 19. （2024•山东开学）杭州第19届亚运会跳水比赛于2023年9月30日至10月4日在杭州奥体中心游泳 馆举行。我国跳水运动员包揽了全部的10枚金牌，真正做到了“十全十美”。如图甲所示为10米跳台冠军 杨昊比赛时的精彩瞬间。图乙对跳水过程进行了模拟，假设将杨昊看作质点，0时刻杨昊到达最高点A，此后 做自由落体运动，t时刻到达标记点B，3t时刻到达落水点C，已知BC的高度为9.6m，则AC的高度为（ ） A．10m B．10.4m C．10.8m D．11.2m 【解答】解：从最高点开始杨昊做自由落体运动，从A到B的时间为t，从B点到C点的时间为2t，取时间间 隔为t，根据相同时间间隔位移之比为 1：3：5，则AB段位移与BC段位移之比为1：8，则AC的高度为 9 ℎ =9.6× m=10.8m。 8 故选：C。 20. （2024•成都开学）一名宇航员在某星球上完成自由落体运动实验，让一小球从一定的高度自由下落，测得小球第5s内的位移大小为18m（此时小球还未落地）。下列说法正确的是（ ） A．该星球上的重力加速度大小为g＝9.8m/s2 B．小球第5s内的平均速度大小为3.6m/s C．小球第5s末的速度大小为10m/s D．小球第2s内的位移大小为6m 1 【解答】解：A、根据 x= gt2 ，设t ＝4s，t ＝5s 2 1 2 1 1 可得Δx= gt2− gt2 2 2 2 1 且Δx＝18m 代入数据解得星球上的重力加速度大小为 g＝4m/s2 故A错误； 18 B、小球第5s内的平均速度大小 v= m/s=18m/s，故B错误； 1 C、小球第5s末的速度大小v＝gt 代入数据解得v＝20m/s，故C错误； D、设t＝2s，t′＝1s 1 1 小球第2s内的位移大小x = gt2− gt'2 2 2 2 代入数据解得x ＝6m，故D正确。 2 故选：D。 21. （2023秋•东城区期末）在地铁某路段的隧洞墙壁上，连续相邻地挂有相同的广告画，画幅的宽度为 0.8m，在列车行进的某段时间内，由于视觉暂留现象，车厢内的人向窗外望去会感觉广告画面是静止的。若 要使人望向窗外时，看到的是画中的苹果做自由落体运动，则这段时间内（人眼的视觉暂留时间取 0.05s，重 力加速度g取10m/s2）（ ） A．列车的车速为8m/s B．隧洞墙壁上每幅画中苹果所在的位置可连成抛物线 C．隧洞墙壁上相邻两幅画中苹果之间的高度差都相等 D．隧洞墙壁上连续相邻两幅画中苹果之间的高度差不相等，依次相差5cm 【解答】解：A、地铁移动速度达到相邻图片时间间隔为0.05s时，可以认为广告画面静止，所以列车速度为 x 0.8 v= = m/s=16m/s， t 0.05 故A错误； B、以匀速行驶的列车为参考系，画中的苹果是自由落体运动，则在以地面为参考系的画中苹果任意时刻水平方向的位置与列车相同，竖直方向自由落体的位置，因此隧洞墙壁上每幅画中苹果所在的位置可连成抛物线， 故B正确； C、列车匀速直线运动，每隔相等时间通过一幅画，则苹果在竖直方向的自由落体运动，连续相等时间内的位 移之比是1：3：5：…：（2n﹣1），隧洞墙壁上相邻两幅画中苹果之间的高度差不相等，故C错误； D、根据Δy＝gT2可得隧洞墙壁上连续相邻两幅画中苹果之间的高度差的差值为 Δy＝gT2＝10×（0.05）2m＝2.5cm 故D错误。 故选：B。 题型9竖直上抛运动的基本规律的应用 22. （2023秋•齐齐哈尔期末）小球被竖直向上抛出，如图所示为小球向上做匀减速直线运动时的频闪照 片，频闪仪每隔0.05s闪光一次，测得ac长为23cm，af长为34cm，下列说法正确的是（ ） A．bc长为13cm B．小球通过f点时的速度大小为0.6m/s C．小球通过d点时的速度大小为2.2m/s D．小球的加速度大小为12m/s2 【解答】解：C.匀变速直线运动中，某段的平均速度等于这段中间时刻的瞬时速度，则 x v = cf d 2T 代入数值可得v ＝1.1m/s d 故C错误； D.根据匀变速直线运动规律，连续相等时间间隔内的位移差为定值，可得x −x =4aT2 ac cfx −x x −(x −x ) 解得：a= ac cf = ac af ac = 12m/s2 4T2 4T2 故D正确； A.根据匀变速直线运动规律，连续相等时间间隔内的位移差为定值，可得 Δx=x −x =aT2 ab bc x +x ＝x ＝0.23m ab bc ac 联立解得x ＝0.1m＝10cm bc 故A错误； B.由速度—时间关系式可得v＝v ﹣aT f d 代入数值，解得v＝0.5m/s， f 故B错误； 故选：D。 23. （2023秋•新市区校级期末）2023年成都大运会乒乓球比赛在高新体育中心举行，来自湖北工业大 学的选手周凯击败来自西南大学的选手徐瑛彬，获得男子乒乓球单打冠军。乒乓球赛场上高抛发球是一种典 型的发球方式，若将乒乓球离开手向上的运动视为竖直方向上的匀减速直线运动，且向上运动的时间为t。设 t t 乒乓球离开手后向上运动第一个 时间内的位移为x ，最后一个 时间内的位移为x ，则x ：x 为（ ） 5 1 5 2 2 1 A．1：9 B．11：1 C．9：1 D．1：5 【解答】解：采取逆向思维，看成是初速度为0的匀加速直线运动。根据初速度为0的匀加速直线运动在连续 相等的时间内的位移之比为1：3：5：7：9：11：13⋅⋅⋅，可知 x ：x ＝9：1，故C正确，ABD错误。 2 1 故选：C。 24. （2023秋•石家庄期末）长为L＝1.0m的空心管AB沿竖直方向固定，下端管口B距离地面的高度为 h ＝1.0m，小球a从距离上端管口h ＝1.8m处沿管的轴线由静止释放，同时小球b由地面以初速度v ＝6m/s 2 1 0 沿管的轴线竖直上抛，两小球的直径均小于管的直径，不考虑空气阻力，重力加速度为g＝10m/s2，则以下说 法正确的是（ ）A．a、b两球在管口A上方相遇 B．a、b两球在管内相遇 C．a、b两球在管口B下方空中相遇 D．a、b两球不能在空中相遇 【解答】解：设a球下落h 所用时间t 1 1 1 则ℎ = gt2 1 2 1 √2ℎ √2×1.8 解得t = 1= s=0.6s 1 g 10 根据速度—位移同时，b球上升的最大高度 v2 62 H= 0 = m=1.8m 2g 2×10 v 6 根据速度—时间公式，b球上升的时间为t= 0= s=0.6s g 10 当a球自由下落到管口A时，b球上升到管内，距离上端管口 h ＝L+h ﹣H＝1m+1m﹣1.8m＝0.2m 3 2 处，此时v ＝gt ＝10×0.6m/s＝6m/s a 1 1 1 设a球追上b球下落距离h ，追上时有v t + gt2− gt2= ℎ 4 a 2 2 2 2 2 3 1 解得t = s 2 30 1 1 1 1 2 37 则有ℎ =v t + gt2=6× m+ ×10×( ) m= m＜L 4 a 2 2 2 30 2 30 180 所以a、b两球在管内相遇。 故ACD错误，B正确。 故选：B。第 3 讲 重力 弹力 摩擦力 1、理解重力及重心的概念。 2、会判断弹力的方向和求其大小。 3、掌握和理解摩擦力方向的判断和大小的求解。考点一 弹力的分析与计算 1．弹力有无的判断 (1)条件法：根据物体是否直接接触并发生弹性形变来判断是否存在弹力．此方法多用来判断形变较明显的情况． (2)假设法：对形变不明显的情况，可假设两个物体间弹力不存在，看物体能否保持原有的状态，若运动状态不变， 则此处不存在弹力，若运动状态改变，则此处一定有弹力． (3)状态法：根据物体的运动状态，利用牛顿第二定律或共点力平衡条件判断弹力是否存在． (4)替换法：可以将硬的、形变不明显的施力物体用软的、易产生明显形变的物体来替换，看能否维持原来的运动 状态． 2．弹力方向的判断 (1)根据物体所受弹力方向与施力物体形变的方向相反判断． (2)根据共点力的平衡条件或牛顿第二定律确定弹力的方向． 3．弹力大小计算的三种方法： (1)根据力的平衡条件进行求解． (2)根据牛顿第二定律进行求解． (3)根据胡克定律进行求解． ①内容：弹簧发生弹性形变时，弹力的大小F跟弹簧伸长(或缩短)的长度x成正比． ②表达式：F＝kx.k是弹簧的劲度系数，单位为N/m；k的大小由弹簧自身性质决定．x是弹簧长度的变化量，不是 弹簧形变以后的长度． [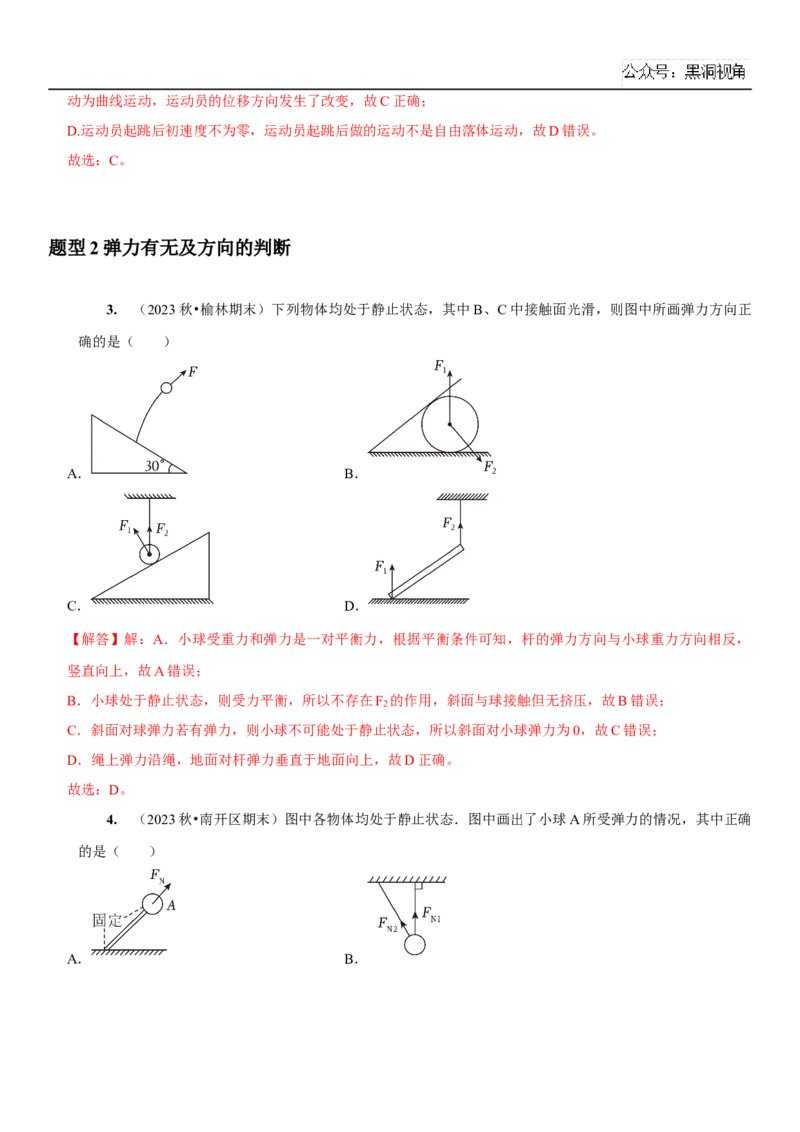例题1] （2024•宿迁一模）某运动员以如图所示的姿势蹲在水平地面上，则该运动员（ ） A．受到的支持力是由于脚掌形变产生的 B．对地面的压力就是重力 C．受到的支持力和重力是一对平衡力 D．一定受到摩擦力 【解答】解：A．运动员受到的支持力是由于水平地面的形变产生的，故A错误； B．运动员对地面的压力是运动员对水平地面的挤压，施力物体是人，受力物体是地面，作用点在地面上，属 于弹力，运动员受到的重力是地球对运动员的作用力，施力物体是地球，受力物体是人，作用点在人的重心上，是由于万有引力的吸引而产生的，所以运动员对地面的压力不是重力，故B错误； C．由平衡条件可知运动员受到的支持力和重力大小相等，方向相反，是一对平衡力，故C正确； D．运动员以题图所示的姿势蹲在水平地面上，处于平衡状态，在水平方向没有相对运动，也没有相对运动的 趋势，因此不受摩擦力的作用，故D错误。 故选：C。 [例题2] （2023秋•辛集市期末）2023年杭州亚运运会上，来自中国天才选手全红婵频频上演“水花消 失术”，10米台决赛第二轮的第二跳，7名裁判全部给出10分。下列说法正确的是（ ） A．跳水过程全红婵的重心一直都在自己身上且重心位置相对自己是不变的 B．跳台受到的压力就是运动员的重力 C．研究全红婵在女子10米台决赛中的姿态，全红婵可看作质点 D．全红婵受到的支持力，是因为跳台发生形变而产生的 【解答】解：A，跳水过程全红婵的姿态在改变，重心位置相对自己是改变的，故A错误； B.跳台受到的压力是运动员施加的，运动员的重力是地球施加的，不是同一个力，故B错误； C.研究全红婵在女子10米台决赛中的姿态，全红婵身体的形状不可忽略，所以不能把全红婵看作质点，故 C错 误； D.根据弹力的产生条件，全红婵受到的支持力，是因为跳台发生形变而产生的，故D正确。 故选：D。 [例题3] （2024•浉河区校级模拟）“学以致用”是学习的好习惯，一位女生仅借助橡皮筋，刻度尺就测 出了课本与桌面间的动摩擦因数。她先用刻度尺测出橡皮筋的自然长度 L ，然后用皮筋将课本悬挂起来，当 0 课本静止时测出橡皮筋的长度为L ，接下来用像皮筋沿水平桌面拉动课本，当课本匀速运动时橡皮筋的长度 1 为L 。橡皮筋的形变始终处于弹性限度内，所产生的弹力与形变址的关系遵循胡克定律。由此可知，课本与 2 桌面间的动摩擦因数为（ ） L −L L −L 2 0 1 0 A． B． L −L L −L 1 0 2 0 L −L L −L 2 1 2 1 C． D． L −L L −L 1 0 2 0 【解答】解：依题意，将课本用皮筋悬挂起来，当课本静止时测出橡皮筋的长度为L ，则 1k（L ﹣L ）＝mg 1 0 然后用像皮筋沿水平桌面拉动课本，当课本做匀速直线运动时，橡皮筋的长度为 L ，由平衡条件可得k（L ﹣ 2 2 L ）＝μmg 0 L −L 联立解得μ= 2 0 L −L 1 0 故A正确；BCD错误。 故选：A。 [例题4] （2023秋•温州期末）如图所示，弹簧一端固定在墙壁上，另一端与物块相连接。为使物块能在 粗糙水平面上保持静止，弹簧的最大长度为l ，最小长度为l 。由此可知弹簧的原长是（ ） 1 2 l −l l +l l l A． 1 2 B． 1 2 C．l + 1 D．l − 2 2 2 2 2 1 2 【解答】解：使物块能在粗糙水平面上保持静止，弹簧的最大长度为l ，设弹簧的原长为l ，则根据胡克定律 1 0 和平衡条件有k（l ﹣l ）＝f ，同理最小长度为l ，则根据胡克定律和平衡条件有k（l ﹣l ）＝f ，解得l 1 0 max 2 0 2 max 0 l +l = 1 2，故B正确，ACD错误。 2 故选：B。 考点二 滑轮模型与死结模型问题 1．死结模型：如几个绳端有“结点”，即几段绳子系在一起，谓之“死结”，那么这几段绳中的张力不一定相等． 2．注意：轻质固定杆的弹力方向不一定沿杆的方向，作用力的方向需要结合平衡方程或牛顿第二定律求得，而轻 质活动杆中的弹力方向一定沿杆的方向． [例题5] （2023秋•新市区校级期末）如图甲所示，一架直梯斜靠光滑的竖直墙壁上，下端放在粗糙的水 平地面上，直梯处于静止状态。从侧面观察时，可画成如图乙所示的图形。从图乙的角度观察，下列说法中 正确的是（ ）A．地面对梯子的弹力是由于梯子发生形变而产生的 B．地面对梯子的弹力方向沿梯子指向左上方 C．地面对梯子的作用力方向竖直向上 D．梯子对地面的摩擦力方向水平向右 【解答】解：A、地面对梯子的弹力是由于地面发生形变而产生，故A错误； B、地面对梯子的弹力方向竖直向上，故B错误； C、地面对梯子的作用力方向，即弹力和摩擦力的合力方向斜向左上方，故C错误； D、梯子对地面的摩擦力方向水平向右，故D正确； 故选：D。 [例题6] （2023秋•长寿区期末）如图为仰韶文化时期的尖底瓶，装水后的尖底瓶“虚则欹、中则正、满 则覆”的特点，关于装水后的尖底瓶，下列说法正确的是（ ） A．瓶所受的重力就是瓶对支架的压力 B．装入瓶中的水越多，瓶的重心一定越高 C．瓶的重心是瓶各部分所受重力的等效作用点 D．瓶的重心一定在瓶身上 【解答】解：A、重力是由于地球吸引而产生的力，瓶为受力物体，而压力的施力物体为瓶，所以两个力并非 是同一个力，故A错误； BC、重心为重力的等效作用点，重心的位置与物体质量分布有关，装入瓶中的水越多，瓶的重心不一定升高， 故B错误，C正确； D、重心位置不一定在物体上，可以在物体外，故D错误； 故选：C。 [例题7] （2024•福清市校级开学）质量分别为 1kg、2kg、1kg的木块a、b、c和两个劲度系数均为 500N/m的相同轻弹簧p、q用轻绳连接，如图所示，其中a放在光滑水平桌面上。开始时p弹簧处于原长，木块都处于静止状态。现用水平力 F缓慢地向左拉p弹簧的左端，直到c木块刚好离开水平地面为止，g取 10m/s2。该过程p弹簧的左端向左移动的距离是 cm。 【解答】解：开始未用水平力拉弹簧p时，弹簧q处于压缩状态，受到的压力等于b物体的重力，根据胡克定 m g 律，弹簧q压缩的长度为x = b 1 k 代入数据解得x ＝4cm 1 当c木块刚好要离开水平地面时，弹簧q处于伸长的状态，受到的拉力等于c物体的重力，根据胡克定律，弹 m g 簧q的伸长长度x = c 2 k 代入数据解得x ＝2cm 2 m g+m g 此时，弹簧p处于伸长状态，受到的拉力等于b、c的总重力，p的伸长长度x = c b 3 k 代入数据解得 4mg x ＝6cm；根据几何关系得到，该过程p弹簧的左端向左移动的距离为：s=x +x +x = 3 1 2 3 k 代入数据解得s＝12cm 故答案为：12cm。 [例题8] （2024•鲤城区校级模拟）越来越多的人喜欢挑战极限，如图是两位“勇士”参与溜索活动，两 倾斜的钢丝拉索分别套有M、N两个滑轮（滑轮与绳之间有可调节的制动片），两滑轮上用安全带系着两位 “勇士”，当他们都沿拉索向下滑动时，M上的带子与索垂直，N上的带子始终竖直向下，则以下判断正确 的是（ ） A．M情况中，滑轮与索之间有摩擦力 B．N情况中，滑轮与索之间无摩擦力 C．M情况中“勇士”做匀速直线运动D．N情况中“勇士”做匀速直线运动 【解答】解：AC、设钢索与水平面夹角为θ，对M滑轮下的勇士进行受力分析可知，由于M上的带子与索垂 直，加速度a＝gsinθ，因此与滑轮M一起斜向下做加速运动，对M滑轮与勇士整体受力分析，二者加速度相同， 等于gsinθ，M不受摩擦力，故AC错误； BD、对N的勇士受力分析，只受重力和竖直向上的绳上的拉力，合外力为 0，此时为匀速直线运动，再对N滑 轮与勇士整体受力分析，想要匀速直线运动，N与索道之间必定有摩擦，故B错误，D正确； 故选：D。 考点三 摩擦力的分析与计算 1．静摩擦力 (1)有无及其方向的判定方法 ①假设法：假设法有两种，一种是假设接触面光滑，不存在摩擦力，看所研究物体是否改变原来的运动状态．另 一种是假设摩擦力存在，看所研究物体是否改变原来的运动状态． ②状态法：静摩擦力的大小与方向具有可变性．明确物体的运动状态，分析物体的受力情况，根据平衡方程或牛 顿第二定律求解静摩擦力的大小和方向． ③牛顿第三定律法：此法的关键是抓住“力是成对出现的”，先确定受力较少的物体受到的静摩擦力的方向，再 根据“力的相互性”确定另一物体受到的静摩擦力的方向． (2)大小的计算 ①物体处于平衡状态(静止或匀速直线运动)，利用力的平衡条件来判断其大小． ②物体有加速度时，若只有静摩擦力，则F＝ma.若除静摩擦力外，物体还受其他力，则F ＝ma，先求合力再求 f 合 静摩擦力． 2．滑动摩擦力 (1)方向：与相对运动的方向相反，但与物体运动的方向不一定相反． (2)计算：滑动摩擦力的大小用公式F ＝ μF 来计算，应用此公式时要注意以下几点： f N ①μ为动摩擦因数，其大小与接触面的材料、表面的粗糙程度有关；F 为两接触面间的正压力，其大小不一定等于 N 物体的重力． ②滑动摩擦力的大小与物体的运动速度和接触面的大小均无关． [例题9] （2024•邵阳一模）中央广播电视总台《2024年春节联欢晚会》以“龙行龘龘，欣欣家国”为主 题。中国书法历史悠久，是中华民族优秀传统文化之一。如图所示，书法家在水平桌面上平铺一张白纸，为 防打滑，他在白纸的左侧靠近边缘处用镇纸压住。书写“龙”字“一”这一笔画时，在向右行笔的过程中镇 纸和白纸都保持静止，则（ ）A．毛笔对白纸的摩擦力向左 B．白纸对镇纸的摩擦力向右 C．桌面对白纸的摩擦力向左 D．桌面对白纸的摩擦力小于毛笔对白纸的摩擦力 【解答】解：A．书写“龙”字“一”这一笔画时，毛笔向右运动，白纸相对毛笔白纸向左运动，毛笔对白纸 的摩擦力向右，故A错误； B．镇纸相对白纸无运动趋势，白纸与镇纸间没有摩擦力，故B错误； CD．对白纸受力分析，白纸受到桌面对白纸的摩擦力与毛笔对白纸的摩擦力，二力平衡，方向相反，大小相等， 则桌面对白纸的摩擦力向左，桌面对白纸的摩擦力等于毛笔对白纸的摩擦力，故C正确，D错误。 故选：C。 [例题10]（2024•丰台区一模）如图所示，木块A、B分别重50N和60N与水平地面之间的动摩擦因数均 为0.2。夹在A、B之间的轻弹簧被压缩了2cm，弹簧的劲度系数为400N/m。用F＝2N的水平拉力拉木块B， 木块A、B均保持静止。最大静摩擦力近似等于滑动摩擦力，下列说法正确的是（ ） A．弹簧的弹力大小为80N B．木块A受到的摩擦力大小为10N C．木块B受到的摩擦力大小为6N D．地面给A、B组成的系统的摩擦力大小为2N 【解答】解：A、B与地面之间的最大静摩擦力大小为f ＝μG ＝0.2×50N＝10N，f ＝μG ＝0.2×60N＝12N Am A Bm B A、x＝2cm＝0.02m，弹簧的弹力大小为F'＝kx＝400×0.02N＝8N，故A错误； B、因A物块处于静止状态，根据平衡条件得A所受摩擦力大小为f ＝F'＝8N，故B错误； A C、在水平方向上B受弹簧对它向右的弹力，向右的拉力，以及向左的摩擦力，根据平衡条件可得 f ＝F+F'＝ B 8N+2N＝10N，故B受摩擦力大小为10N，故C错误； D、把A、B两物块以及弹簧看成一个整体，由平衡条件可得整体所受摩擦力大小f＝F＝2N，故D正确。 故选：D。 [例题11] （2023秋•雁塔区期末）如图所示，重为5N的书本被20N的水平力F压在竖直墙面上处于静止状态。书本所受静摩擦力（ ） A．大小为5N B．大小为20N C．方向竖直向下 D．方向水平向右 【解答】解：由于书本保持静止，由平衡条件可知，摩擦力f＝G＝5N，方向竖直向上；故A正确，BCD错误。 故选：A。 [例题12]（2023秋•台州期末）自行车的机械碟刹可以让车辆拥有更好的制动性，碟刹是由碟刹器与碟刹 片两者间的摩擦力实现制动的。在一次缓慢刹车的过程中，下列说法正确的是（ ） A．碟刹器受到的是静摩擦力 B．增大碟刹器与碟刹片的正压力可以增大摩擦力 C．增大碟刹器与碟刹片的正对面积可以增大摩擦力 D．碟刹器受到的摩擦力方向一定与碟刹片的运动方向相反 【解答】解：A．碟刹器与碟刹片具有相对运动，所以碟刹器受到的是滑动摩擦力，故A错误； BC．根据f＝μF 可知，碟刹器与碟刹片之间的滑动摩擦力与碟刹器与碟刹片的正对面积无关，与动摩擦因数μ N 以及碟刹器与碟刹片的正压力F 有关，增大碟刹器与碟刹片的正压力可以增大滑动摩擦力，故C错误，B正确； N D．根据滑动摩擦力方向与相对运动方向相反可知，碟刹器上受到的摩擦力方向与其相对碟刹片的运动方向相 反，故D错误。 故选：B。 考点四 摩擦力的突变问题 [例题13]（多选）（2023秋•秦州区校级期末）水平木板上有质量m＝3kg的物块，受到随时间t按一定规律变化的水平拉力F的作用，如图甲所示，用力传感器测出相应时刻物块所受摩擦力F 的大小如图乙所示， f 取重力加速度g＝10m/s2，下列判断正确的是（ ） A．t＝1s时外力F一定等于零 B．t＝7s时外力F一定等于3N C．物块与木板间的动摩擦因数为0.1 D．物块与木板间的动摩擦因数为0.13 【解答】解：A、由题意可知水平木板表面粗糙，因为物块在水平方向上的摩擦力在t＝1s 时为零，若受到不为 零的外力F作用，则必定会产生摩擦力，故互相矛盾，因此t＝1s时，F＝0，故A正确； B、由图可知，物块受到的最大静摩擦力为4N，外力需要大于最大静摩擦力才可能让该物体受到的摩擦力从静 摩擦力变成滑动摩擦力，而在t＝7s 时，该物体受到的摩擦力等于滑动摩擦力，所以外力F必定大于最大静摩 擦力4N，故B错误； f 3 CD、由图可知，物体受到的滑动摩擦力f＝3N，因为f＝μmg，动摩擦因数：μ= = =0.1，故C正确， mg 3×10 D错误。 故选：AC。 [例题14]（2023秋•和平区校级期中）如图所示，打印机进纸槽里叠放有一叠白纸，进纸时滚轮以竖直向 下的力F压在第一张白纸上，并沿逆时针方向匀速转动，滚轮与第一张纸不打滑，但第一张纸与第二张纸间 发生相对滑动。设最大静摩擦力与滑动摩擦力相等。滚轮与白纸之间的动摩擦因数为μ ，白纸之间、白纸与 1 纸槽底座之间的动摩擦因数均为μ ，每张白纸的质量为m，不考虑静电力的影响，重力加速度为g，则下列说 2 法正确的是（ ） A．滚轮对第一张白纸的摩擦力方向水平向左 B．第二、三张白纸间的摩擦力大小为μ （F+2mg） 2 C．第三、四张白纸间的摩擦力大小为μ （F+mg） 2D．越靠近底座，白纸间的摩擦力越大 【解答】解：A．第1张纸在滚轮的摩擦力作用下向右运动，第一张纸相对于滚轮的运动趋势方向向左，则滚 轮对第一张白纸的摩擦力方向向右，故A错误； B．第一、二张白纸间的摩擦力为滑动摩擦力，大小为 f ＝μ （F+mg）；第二张白纸处于静止状态，第二、三 12 2 张白纸间的摩擦力为静摩擦力，大小等于第一、二张白纸间的摩擦力，即f ＝f ＝μ （F+mg），故B错误； 23 12 2 C．第三张白纸处于静止状态，第三、四张白纸间的摩擦力为静摩擦力，大小等于第二、三张白纸间的摩擦力， 即f ＝f ＝μ （F+mg），故C正确； 34 23 2 D．除第一张白纸外，其余所有白纸均处于静止状态，白纸间的摩擦力均为μ （F+mg），大小相等。故D错误。 2 故选：C。 [例题15]（2023春•巴彦淖尔期末）如图所示，一质量为m的木块在水平力F的作用下静止在竖直粗糙墙 壁上，已知木块与墙壁之间的最大静摩擦力等于滑动摩擦力，重力加速度大小为g，木块与墙壁间的动摩擦因 数为μ，下列说法正确的是（ ） A．若水平力F增大，木块受到的摩擦力也增大 B．若撤去F，木块受到的滑动摩擦力大小等于mg C．若撤去F，木块受到的滑动摩擦力大小等于μmg D．若撤去力F，木块将自由下落 【解答】解：A、对木块进行受力分析，根据平衡条件可得 mg＝f，F ＝F N 水平力F增大，木块受到墙壁对其弹力将增大，摩擦力不变，故A错误； BCD、若产生静摩擦力，物体必须对接触面产生压力且有相对运动的趋势，若产生滑动摩擦力，物体必须对接 触面产生压力且发生相对运动，而若撤去F，木块将不再紧压墙壁，即压力为零，因此摩擦力将为0，木块将自 由下落，故BC错误，D正确。 故选：D。 [例题16]（2023春•杭州期中）某同学利用图甲所示装置研究摩擦力的变化情况。实验台上固定一个力传 感器，传感器用棉线拉住物块，物块放置在粗糙的长木板上。水平向左的力T拉木板，传感器记录的F﹣t图 像如图乙所示。下列说法正确的是（ ）A．实验中必须让木板保持匀速运动 B．图乙中曲线就是T的大小随时间变化的曲线 C．只用图乙中数据可得出物块与木板间的动摩擦因数 D．最大静摩擦力与滑动摩擦力之比约为10：7 【解答】解：AB．为了能研究摩擦力随时间的变化曲线，故物块一直要处于静止状态，根据平衡条件可知向左 的摩擦力和向右轻绳的拉力大小相等，图乙是轻绳向右的拉力随时间变化曲线，故图乙也可以反映摩擦力随时 间变化的曲线，由图乙可知轻绳向右的拉力先增大后减小，最后趋于不变，故物块先受静摩擦力作用后受滑动 摩擦力作用，所以不需要让木板保持匀速运动，故AB错误； C．根据滑动摩擦力的计算公式 f＝μF ＝μmg N 可知，由于不知道物块的重力，故无法求出物块与木板间的动摩擦因数，故C错误； D．由图可知，最大静摩擦力约为10N，滑动摩擦力约为7N，故最大静摩擦力与滑动摩擦力之比约为10：7， 故D正确。 故选：D。 题型1重力 重心 1. （2024•鹿城区校级模拟）如图所示，“马踏飞燕”是汉代艺术家高度智慧、丰富想象、浪漫主义精 神和高超的艺术技巧的结晶，是我国古代雕塑艺术的稀世之宝。飞奔的骏马之所以能用一只蹄稳稳地踏在飞 燕上，是因为马的重心位置和飞燕（视为质点）在一条竖直线上。下列关于重力和重心的说法中正确的是（ ）A．只有静止的物体才受到重力作用 B．这件艺术品的重力大小总是恒定的 C．物体挂在弹簧测力计下，弹簧测力计的示数一定等于物体的重力 D．质量分布均匀形状规则物体的重心一定在其几何中心，但不一定在物体上 【解答】解：A、物体是否受到重力与运动状态无关，地面附近一切物体无论处于何种运动状态，都受到重力 的作用，故A错误； B、在地球上不同位置重力加速度不同，故重力G＝mg不同，故B错误； C、物体挂在弹簧测力计下，竖直处于平衡状态时，弹簧测力计的示数等于物体的重力，当弹簧测力计和物体 有加速度时，示数不等于物体的重力，故C错误； D、质量分布均匀形状规则物体的重心一定在其几何中心，但不一定在物体上，故D正确； 故选：D。 2. （2023秋•龙华区期末）如图所示为中国选手苏翊鸣参加北京 2022年冬奥会首钢滑雪大跳台决赛中 的频闪照片。运动员从高处滑下，通过起跳台起跳，完成各种空翻、转体、抓板等技术动作后落地，以下说 法正确的是（ ） A．研究运动员在空中的动作完成情况时，可以将他看成质点 B．助滑时运动员两腿尽量深蹲是为了降低重心、增大重力 C．腾空中曝光时间间隔内，运动员的位移方向发生了改变 D．运动员起跳后做自由落体运动 【解答】解：A.研究运动员在空中的动作完成情况时，运动员的形状、大小不能忽略，不可以将他看成质点， 故A错误； B.助滑时运动员两腿尽量深蹲是为了降低重心增大了自身的稳定性，运动员的质量不变，重力不变，故B错误； C.忽略空气阻力，腾空中曝光时间间隔内，运动员水平方向做匀速直线运动，竖直方向做竖直上抛运动，合运动为曲线运动，运动员的位移方向发生了改变，故C正确； D.运动员起跳后初速度不为零，运动员起跳后做的运动不是自由落体运动，故D错误。 故选：C。 题型2弹力有无及方向的判断 3. （2023秋•榆林期末）下列物体均处于静止状态，其中B、C中接触面光滑，则图中所画弹力方向正 确的是（ ） A． B． C． D． 【解答】解：A．小球受重力和弹力是一对平衡力，根据平衡条件可知，杆的弹力方向与小球重力方向相反， 竖直向上，故A错误； B．小球处于静止状态，则受力平衡，所以不存在F 的作用，斜面与球接触但无挤压，故B错误； 2 C．斜面对球弹力若有弹力，则小球不可能处于静止状态，所以斜面对小球弹力为0，故C错误； D．绳上弹力沿绳，地面对杆弹力垂直于地面向上，故D正确。 故选：D。 4. （2023秋•南开区期末）图中各物体均处于静止状态．图中画出了小球A所受弹力的情况，其中正确 的是（ ） A． B．C． D． 【解答】解：A、球受重力和弹力，根据平衡条件，杆对小球的力应竖直向上，故A错误； B、F 应为零，该绳没有发生形变，否则球不能平衡，故B错误； N2 C、球受重力、下面球的弹力和墙壁的支持力，两个支持力均垂直于接触面，故C正确； D、大半圆对小球的支持力F 应是沿过小球与圆接接触点的半径，且指向圆心的弹力，故D错误； N2 故选：C。 5. （2023秋•重庆期末）网上热传一段视频，唤醒了“80、90后”的记忆，奶奶站在凳子上用杆秤给 小孙子称体重，多才的网友根据视频画了一幅漫画，如图所示，则下列说法正确的是（ ） A．奶奶对凳子的压力是由于凳子的形变引起的 B．小孩所受的重力方向一定指向地球球心 C．凳子对奶奶的支持力与奶奶所受的重力是一对平衡力 D．小孩的重心一定位于秤钩的正下方 【解答】解：A.奶奶对凳子的压力是由于奶奶的形变引起的，故A错误； B.小孩所受的重力方向一定竖直向下，垂直于水平面，不一定指向地球球心，故B错误； C.凳子对奶奶的支持力与奶奶所受的重力合小孩所受重力的和，是一对平衡力，故C错误； D.小孩受重力和秤钩的拉力，两个力等大反向，小孩的重心一定位于秤钩的正下方，故D正确； 故选：D。 题型3弹力大小的计算 6. （2023秋•南充期末）如图甲所示，一轻弹簧左端与墙壁相连于 O点，作用于右端A点的水平外力F （F未画出）变化时，弹簧长度不断变化，取水平向左为正方向，得到 F与弹簧长度l的关系如图乙所示，下列说法正确的是（ ） A．弹簧原长为5cm B．弹簧的劲度系数为4N/m C．l＝10cm时，弹簧对墙壁的弹力方向水平向左 D．在弹性限度内，弹簧弹力的大小与弹簧长度成正比 【解答】解：A、根据图像可知，当F＝0时，弹簧处于自然伸长状态，即原长为15cm，故A错误； F 40 = = B、由胡克定律可得k N/m＝400N/m，故B错误； x (25−15)×10−2 C、由题意知，弹簧长度l＝10cm时，F方向向左，弹簧处于压缩状态，弹簧对墙壁的弹力水平向左，故C正确； D、根据胡克定律可知，在弹性限度内，弹簧弹力与弹簧的形变量成正比关系，故D错误。 故选：C。 7. （2023•屯昌县二模）如图所示，甲、乙为两根完全相同的轻质弹簧，甲弹簧一端固定在天花板上， 另一端悬挂一质量为m 的物块；乙弹簧一端固定在水平地面上，另一端连接一质量为 m 的物块，两物块静 A B 止时，测得甲、乙两根弹簧的长度分别为l 和l ，已知重力加速度大小为g，两弹簧均在弹性限度内，则这两 1 2 根弹簧的劲度系数为（ ） (m +m )g (m −m )g A B A B A． B． l −l l −l 1 2 1 2 (m +m )g (m −m )g A B A B C． D． l +l l +l 1 2 1 2 【解答】解：设弹簧原长为l ，劲度系数为k，对甲图根据共点力平衡条件得：m g＝k（l ﹣l ） 0 A 1 0 对乙图根据共点力平衡条件得：m g＝k（l ﹣l ） B 0 2 (m +m )g 联立解得：k= A B l −l 1 2 故A正确，BCD错误；故选：A。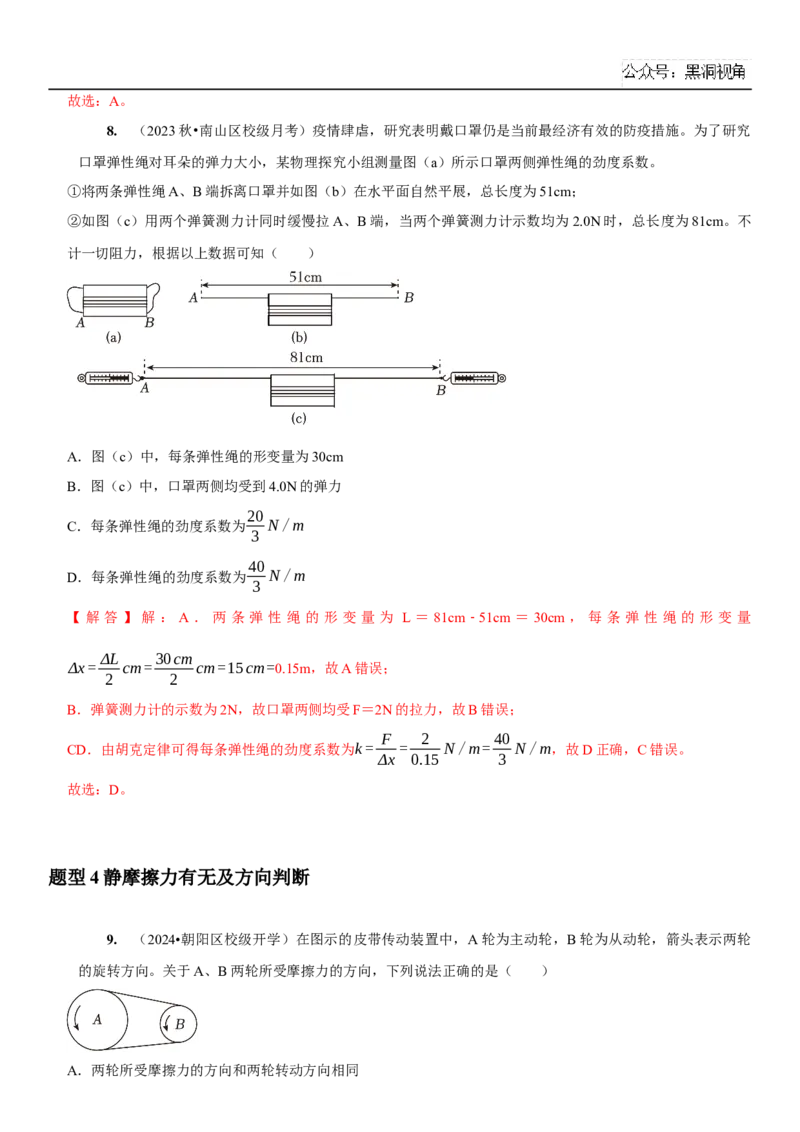 8. （2023秋•南山区校级月考）疫情肆虐，研究表明戴口罩仍是当前最经济有效的防疫措施。为了研究 口罩弹性绳对耳朵的弹力大小，某物理探究小组测量图（a）所示口罩两侧弹性绳的劲度系数。 ①将两条弹性绳A、B端拆离口罩并如图（b）在水平面自然平展，总长度为51cm； ②如图（c）用两个弹簧测力计同时缓慢拉A、B端，当两个弹簧测力计示数均为2.0N时，总长度为81cm。不 计一切阻力，根据以上数据可知（ ） A．图（c）中，每条弹性绳的形变量为30cm B．图（c）中，口罩两侧均受到4.0N的弹力 20 C．每条弹性绳的劲度系数为 N/m 3 40 D．每条弹性绳的劲度系数为 N/m 3 【 解 答 】 解 ： A ． 两 条 弹 性 绳 的 形 变 量 为 L ＝ 81cm﹣51cm ＝ 30cm ， 每 条 弹 性 绳 的 形 变 量 ΔL 30cm Δx= cm= cm=15cm=0.15m，故A错误； 2 2 B．弹簧测力计的示数为2N，故口罩两侧均受F＝2N的拉力，故B错误； F 2 40 CD．由胡克定律可得每条弹性绳的劲度系数为k= = N/m= N/m，故D正确，C错误。 Δx 0.15 3 故选：D。 题型4静摩擦力有无及方向判断 9. （2024•朝阳区校级开学）在图示的皮带传动装置中，A轮为主动轮，B轮为从动轮，箭头表示两轮 的旋转方向。关于A、B两轮所受摩擦力的方向，下列说法正确的是（ ） A．两轮所受摩擦力的方向和两轮转动方向相同B．两轮所受摩擦力的方向和两轮转动方向相反 C．A轮受的摩擦力方向和A轮的转动方向相同，B轮受摩擦力的方向和B轮转动方向相反 D．A轮受的摩擦力方向和A轮的转动方向相反，B轮受摩擦力的方向和B轮转动方向相同 【解答】解：由于A、B两轮所受到的摩擦力为静摩擦力，而相对运动趋势不好找，因此可用假设法来判断其 方向，B轮是从动轮，设B轮和皮带接触面光滑，则B相对于皮带的运动方向与其转动方向相反，即B所受摩 擦力方向与B轮转动方向相同，同理，可以判断A轮所受摩擦力与其转动方向相反。故D正确，ABC错误。 故选：D。 10. （2023秋•厦门期末）如图甲所示，订书机是一种常见的文具，其底座前端有弧形凹柏。压下订书钉 使其穿过纸张后进入弧形凹槽，订书钉在凹槽的作用下向内弯曲后，即可完成装订。如图乙所示，当订书钉 末端被压到弧形凹槽上的A点时，凹槽在A点对订书钉末端的（ ） A．弹力方向竖直向上 B．弹力方向水平向右 C．摩擦力方向沿凹槽A点的切线斜向上 D．摩擦力方向沿凹槽A点的切线斜向下 【解答】解：AB、接触面的弹力方向垂直于接触面指向受力物体，所以A点的弹力方向垂直于过A点的切线 指向订书针；AB错误； CD、摩擦力的方向于相对运动趋势方向相反，所以A点对订书针的摩擦力方向沿切线斜向上，故C正确，D错 误。 故选：C。 11. （2023秋•鼓楼区校级期末）学校试卷扫描机器正常情况下，进纸系统能做到“每次只进一张试卷”， 进纸系统的结构示意图如图所示，设图中刚好有48张相同的试卷，每张试卷的质量均为m，搓纸轮按图示方 向转动带动最上面的第1张试卷向右运动；搓纸轮与试卷之间的动摩擦因数为 μ ，试卷与试卷之间、试卷与 1 底部摩擦片之间的动摩擦因数均为μ ，工作时搓纸轮给第1张试卷压力大小为F。试卷扫描机器正常工作时， 2 下列说法正确的是（ ）A．第2张试卷受到第1张试卷的摩擦力方向向左 B．第10张试卷与第11张之间的摩擦力大小为μ （F+10mg）纸张 2 C．第48张试卷与摩擦片之间的摩擦力为0 μ F+mg D．要做到“每次只进一张纸”应要求 1＞ 摩擦片 μ F 2 【解答】解：A.第1张纸上表面受到搓纸轮施加的静摩擦力f 向右运动，相对与第2张纸向右运动，根据平衡 条件可知，第1张纸必然受到第二张纸向左的摩擦力。根据相 互作用力方向相反的特征，第2张纸受到第1张纸向右的摩擦力，故A错误； BC.第2张与第3张纸之间的摩擦力及第10张纸与摩擦片之间的摩擦力都是静摩擦力，根据受力平衡条件，可 知，大小均为f ，故BC错误； 2 D.搓纸轮对第1张纸的摩擦力最大值为f ＝μ F 1 1 第一张纸受到第二张纸滑动摩擦力f ＝μ （mg+F） 2 2 μ F+mg 要做到“每次只进一张纸”，需满足f ＜f ，即 1＞ 2 1 μ F 2 故D正确。 故选：D。 题型5摩擦力的大小 12. （2023•江苏学业考试）机器人服务人类的场景正步入现实生活中，例如餐厅使用机器人来送餐。某 餐厅的送餐机器人的结构简化为如图所示的示意图，机器人的上表面保持水平，当菜品随着机器人一起做匀 速直线运动时，下列说法正确的是（ ） A．菜品受到的摩擦力方向与其运动方向相同B．菜品受到的合外力始终不变 C．菜品的质量越大，受到的静摩擦力越大 D．菜品受到的摩擦力与菜品和机器人上表面间的动摩擦因数成正比 【解答】解：ACD、菜品随着机器人一起做匀速直线运动，匀速直线运动的合力为零，菜品只受到重力和支持 力的作用，没有受到摩擦力，故ACD错误； B、根据受力平衡的条件可知，菜品受到的合外力为零（不变），故B正确。 故选：B。 13. （2023秋•浙江月考）如图所示，水平桌面上放着一叠作业本，共30本。每本作业本的质量都是 m，作业本间的动摩擦因数为μ ，作业本与桌面间的动摩擦因数为μ ，且μ ＜μ 。现用手对一作业本施一水 1 2 1 2 平力，将第10本作业本快速水平抽出（从上往下数第10本），设最大静摩擦力等于滑动摩擦力，重力加速 度大小为g，则在抽出作业本的过程中，下列说法正确的是（ ） A．桌面可能不受作业本对它摩擦力的作用 B．作业本对桌面的摩擦力为30μ mg 2 C．第11本作业本受到第10本作业本的摩擦力为μ mg 1 D．水平拉力一定大于19μ mg 1 【解答】解：ABC．第十本与第十一本之间摩擦力大小是 f 1 ＝μ 1⋅10mg＝10μ 1 mg 将下面二十本看成整体，由于 f 1 ＜μ 2⋅30mg 所以下面二十本作业相对桌面静止，桌面对其的静摩擦力大小为： f ＝10μ mg 1 1 故ABC错误； D．第十本与第九本之间摩擦力大小为 f 2 ＝μ 1⋅9mg＝9μ 1 mg 若要把第十本抽出，水平拉力 F＞f +f ＝（10+9）μ mg＝19μ mg 1 2 1 1 故D正确。 故选：D。14. （2023秋•海淀区校级期中）根据你对物理概念和规律的理解，下列说法中正确的是（ ） A．静止的物体可能受滑动摩擦力作用，运动的物体可以受静摩擦力作用 B．枪膛中的子弹的加速度约为105m/s2，射出的速度可达1000m/s左右，所以加速度大，速度变化就越大 C．微小的力不能使坚硬的物体发生形变，就没有弹力产生 D．竖直上抛运动的物体到达最高点时速度为零，加速度也为零 【解答】解：A、运动的物体可以受静摩擦力作用，静止的物体也可以受滑动摩擦力作用，比如：正在传送带 上斜向上运行的物体，受到静摩擦力，但是运动的。再如：在地面上滑动的物体，地面受到滑动摩擦力，而地 面是静止的，故A正确； B、由a＝得，Δv＝aΔt，速度变化与两个因素有关，所以加速度大，速度变化不一定大，故B错误； C、有些弹性形变的现象不明显，叫微小形变，两个相互接触的物体发生了微小形变，也有弹力产生，故 C错 误； D、竖直上抛运动的物体到达最高点时速度为零，加速度为g，故D错误。 故选：A。 15. （多选）（2023秋•重庆期中）如图所示，高凳子B放在水平地面上，物块A放在高凳子上表面右 端，给A施加一个水平向左、大小为F的拉力，使物块A在高凳子上表面向左匀速运动，高凳子B仍保持静 止，则物块A在高凳子B上表面运动过程中（ ） A．高凳子B受到物块A的摩擦力与拉力F大小相等，方向相同 B．高凳子B受到地面的摩擦力小于F C．若给A施加拉力F在不断增大，高凳子B仍然保持静止 D．高凳子B可能受到的4个力 【解答】解：A、根据题意，A在水平向左的拉力F作用下做匀速直线运动，则根据平衡条件可知，B给A的 滑动摩擦力水平向右，且大小等于F，而根据牛顿第三定律可知，A给B的滑动摩擦力水平向左，大小等于F， 因此可知，高凳子B受到物块A的摩擦力与拉力F大小相等，方向相同，故A正确； B、由于B处于静止状态，竖直方向受重力、A对B的压力、地面对B的支持力而平衡， 根据平衡条件有：m g+F ＝F B NA N 水平方向受A对B的滑动摩擦力与地面对B的静摩擦力而平衡，根据平衡条件有：F AB ＝f地 而根据以上分析可知：F ＝F AB 因此有：f地 ＝F，故B错误； D、高凳子B一定受到了5个力的作用，分别是重力、地面的支持力和摩擦力、A的压力以及A对B的摩擦力，故D错误； C、由于施加拉力F后A相对于B滑动，二者之间为滑动摩擦力，且可知滑动摩擦力大小等于 F，因此，给A 施加拉力F在不断增大时，滑动摩擦力不变，高凳子B仍然保持静止，故C正确。 故选：AC。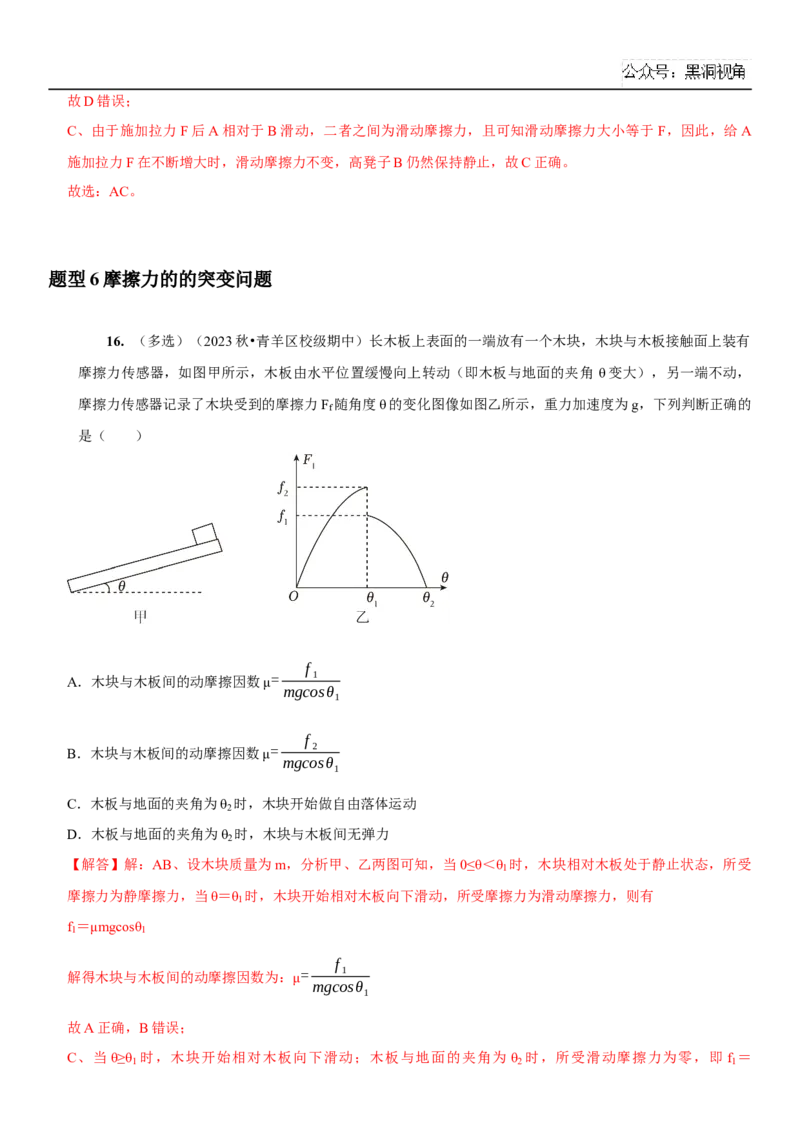 题型6摩擦力的的突变问题 16. （多选）（2023秋•青羊区校级期中）长木板上表面的一端放有一个木块，木块与木板接触面上装有 摩擦力传感器，如图甲所示，木板由水平位置缓慢向上转动（即木板与地面的夹角 θ变大），另一端不动， 摩擦力传感器记录了木块受到的摩擦力F 随角度θ的变化图像如图乙所示，重力加速度为g，下列判断正确的 f 是（ ） f A．木块与木板间的动摩擦因数μ= 1 mgcosθ 1 f B．木块与木板间的动摩擦因数μ= 2 mgcosθ 1 C．木板与地面的夹角为θ 时，木块开始做自由落体运动 2 D．木板与地面的夹角为θ 时，木块与木板间无弹力 2 【解答】解：AB、设木块质量为m，分析甲、乙两图可知，当0≤θ＜θ 时，木块相对木板处于静止状态，所受 1 摩擦力为静摩擦力，当θ＝θ 时，木块开始相对木板向下滑动，所受摩擦力为滑动摩擦力，则有 1 f ＝μmgcosθ 1 1 f 解得木块与木板间的动摩擦因数为：μ= 1 mgcosθ 1 故A正确，B错误； C、当θ≥θ 时，木块开始相对木板向下滑动；木板与地面的夹角为 θ 时，所受滑动摩擦力为零，即 f ＝ 1 2 1μmgcosθ ＝0，可得此时θ ＝90°，木块开始做竖直方向的匀加速运动，但此时在竖直方向的速度不为零，故不 2 2 是自由落体运动（要求初速度为零），故C错误； D、木板与地面的夹角为θ 时（即90°），木块只受重力作用，与木板间无弹力，故D正确。 2 故选：AD。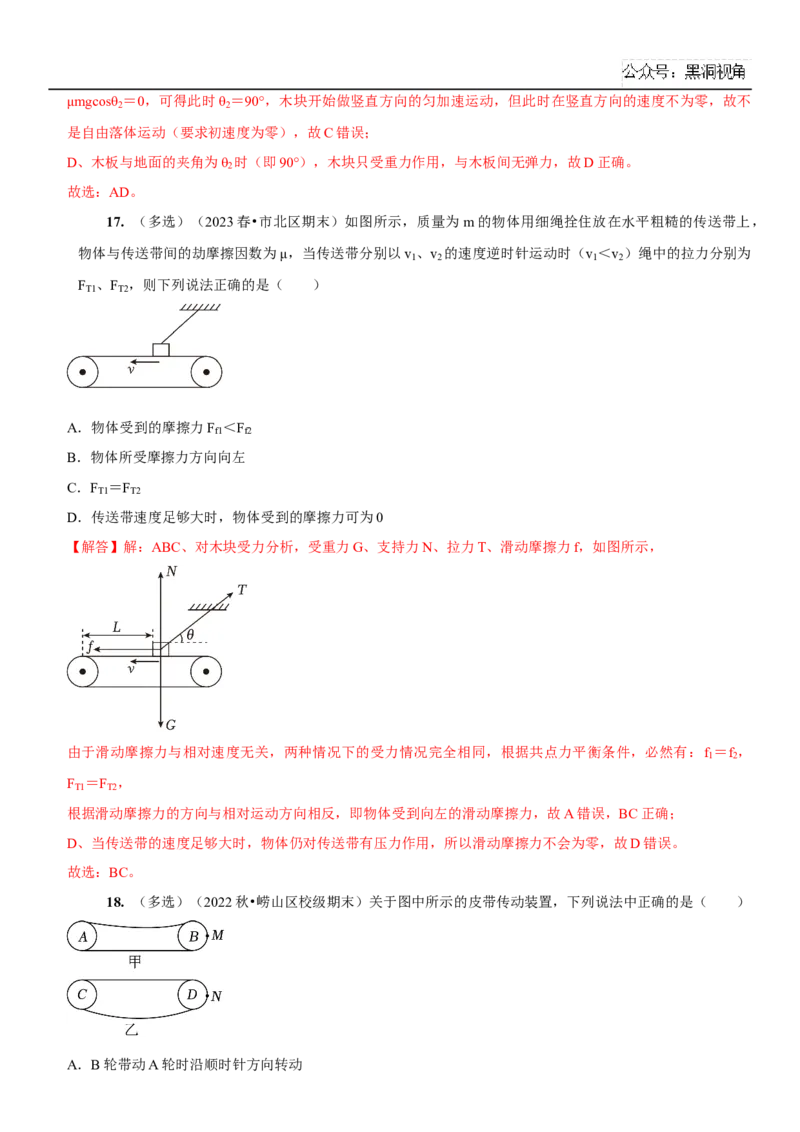 17. （多选）（2023春•市北区期末）如图所示，质量为m的物体用细绳拴住放在水平粗糙的传送带上， 物体与传送带间的劫摩擦因数为μ，当传送带分别以v 、v 的速度逆时针运动时（v ＜v ）绳中的拉力分别为 1 2 1 2 F 、F ，则下列说法正确的是（ ） T1 T2 A．物体受到的摩擦力F ＜F f1 f2 B．物体所受摩擦力方向向左 C．F ＝F T1 T2 D．传送带速度足够大时，物体受到的摩擦力可为0 【解答】解：ABC、对木块受力分析，受重力G、支持力N、拉力T、滑动摩擦力f，如图所示， 由于滑动摩擦力与相对速度无关，两种情况下的受力情况完全相同，根据共点力平衡条件，必然有：f ＝f ， 1 2 F ＝F ， T1 T2 根据滑动摩擦力的方向与相对运动方向相反，即物体受到向左的滑动摩擦力，故A错误，BC正确； D、当传送带的速度足够大时，物体仍对传送带有压力作用，所以滑动摩擦力不会为零，故D错误。 故选：BC。 18. （多选）（2022秋•崂山区校级期末）关于图中所示的皮带传动装置，下列说法中正确的是（ ） A．B轮带动A轮时沿顺时针方向转动B．C轮带动D轮时沿逆时针方向转动 C．轮子上M点所受的静摩擦力方向向上 D．皮带上N点所受的静摩擦力方向向下 【解答】解：A、若A是主动轮，要出现图甲中下方传送带绷紧状态，A轮应带动B轮沿顺时针方向旋转；同 理若B是主动轮，要出现图中下方传送带绷紧状态，上方传送带松弛状态，B轮应带动A轮沿逆时针方向旋转， 故A错误； B、若要出现图乙中上方传送带绷紧状态，下方传送带松弛状态，可以是C作为主动轮带动D轮沿逆时针方向 旋转；也可以是D作为主动轮带动C轮沿顺时针方向旋转，故B正确； C、结合A的分析可知，若A是主动轮，B为从动轮，B轮沿顺时针方向旋转，所以B轮上的M点受到的摩擦 力的方向与运动的方向相同，为向下；若B是主动轮，应为B轮带动A轮沿逆时针方向旋转，此时B轮上的M 点受到的摩擦力的方向与运动的方向相反，也向下，故C错误； D、结合B的分析可知，若C作为主动轮带动D轮沿逆时针方向旋转，皮带相对于轮子有逆时针转动的趋势， 所以皮带上N点所受的静摩擦力方向向下；若是D作为主动轮带动C轮沿顺时针方向旋转，则D轮相对于皮带 有顺时针方向转动的趋势，皮带上N点所受的静摩擦力方向也向下，故D正确。 故选：BD。第 4 讲 力的合成和分解 1、掌握力的合成和分解的方法，能够用这些方法解决实际的物理问题 2、构建活结与死结模型、动杆和定杆模型，总结规律特点。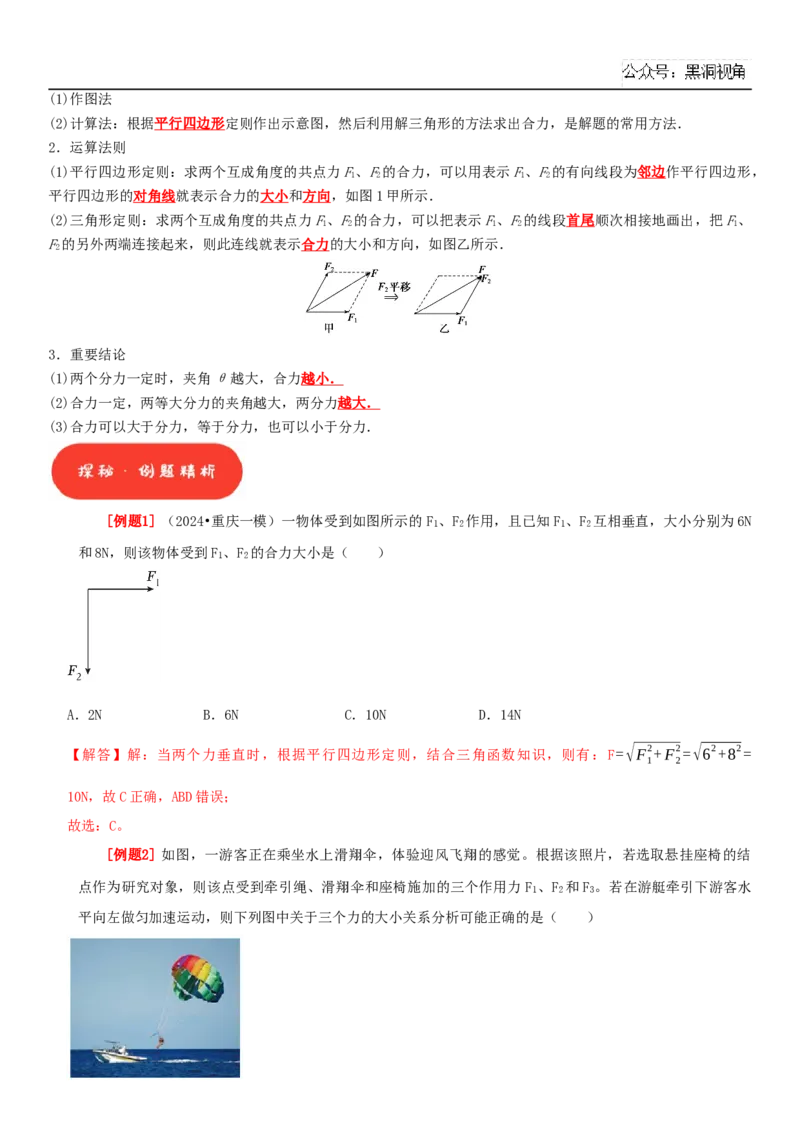 考点一 共点力的合成 1．合成的方法(1)作图法 (2)计算法：根据平行四边形定则作出示意图，然后利用解三角形的方法求出合力，是解题的常用方法． 2．运算法则 (1)平行四边形定则：求两个互成角度的共点力F、F的合力，可以用表示F、F的有向线段为邻边作平行四边形， 1 2 1 2 平行四边形的对角线就表示合力的大小和方向，如图1甲所示． (2)三角形定则：求两个互成角度的共点力F、F的合力，可以把表示F、F的线段首尾顺次相接地画出，把F、 1 2 1 2 1 F的另外两端连接起来，则此连线就表示合力的大小和方向，如图乙所示． 2 3．重要结论 (1)两个分力一定时，夹角θ越大，合力越小． (2)合力一定，两等大分力的夹角越大，两分力越大． (3)合力可以大于分力，等于分力，也可以小于分力． [例题1] （2024•重庆一模）一物体受到如图所示的F 、F 作用，且已知F 、F 互相垂直，大小分别为6N 1 2 1 2 和8N，则该物体受到F 、F 的合力大小是（ ） 1 2 A．2N B．6N C．10N D．14N 【解答】解：当两个力垂直时，根据平行四边形定则，结合三角函数知识，则有：F=√F2+F2=√62+82= 1 2 10N，故C正确，ABD错误； 故选：C。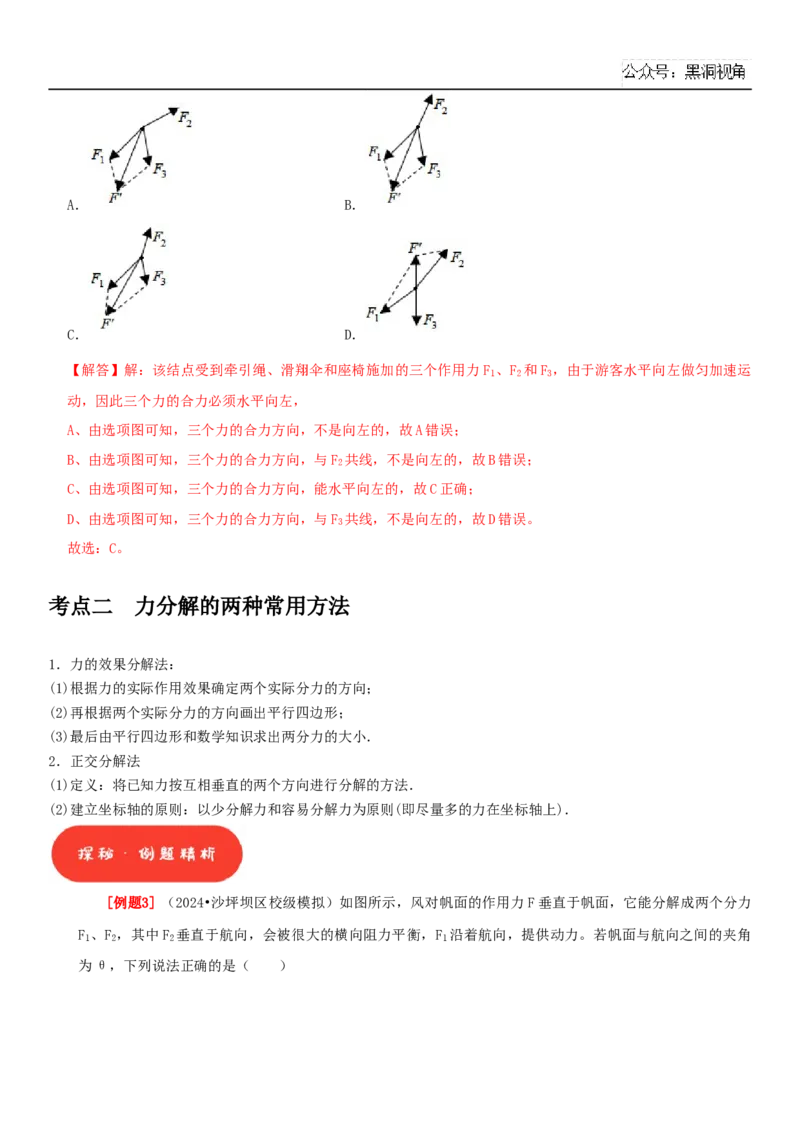 [例题2] 如图，一游客正在乘坐水上滑翔伞，体验迎风飞翔的感觉。根据该照片，若选取悬挂座椅的结 点作为研究对象，则该点受到牵引绳、滑翔伞和座椅施加的三个作用力F 、F 和F 。若在游艇牵引下游客水 1 2 3 平向左做匀加速运动，则下列图中关于三个力的大小关系分析可能正确的是（ ）A． B． C． D． 【解答】解：该结点受到牵引绳、滑翔伞和座椅施加的三个作用力F 、F 和F ，由于游客水平向左做匀加速运 1 2 3 动，因此三个力的合力必须水平向左， A、由选项图可知，三个力的合力方向，不是向左的，故A错误； B、由选项图可知，三个力的合力方向，与F 共线，不是向左的，故B错误； 2 C、由选项图可知，三个力的合力方向，能水平向左的，故C正确； D、由选项图可知，三个力的合力方向，与F 共线，不是向左的，故D错误。 3 故选：C。 考点二 力分解的两种常用方法 1．力的效果分解法： (1)根据力的实际作用效果确定两个实际分力的方向； (2)再根据两个实际分力的方向画出平行四边形； (3)最后由平行四边形和数学知识求出两分力的大小． 2．正交分解法 (1)定义：将已知力按互相垂直的两个方向进行分解的方法． (2)建立坐标轴的原则：以少分解力和容易分解力为原则(即尽量多的力在坐标轴上)． [例题3] （2024•沙坪坝区校级模拟）如图所示，风对帆面的作用力F垂直于帆面，它能分解成两个分力 F 、F ，其中F 垂直于航向，会被很大的横向阻力平衡，F 沿着航向，提供动力。若帆面与航向之间的夹角 1 2 2 1 为θ，下列说法正确的是（ ）A．F ＝F tanθ 2 1 B．F ＝Fsinθ 2 F C．船受到的横向阻力为 cosθ D．船前进的动力为F tanθ 2 【解答】解：AB．根据几何关系可得风对帆面的作用力F与垂直于航向方向的分力F 之间的夹角也等于θ，则 2 F ＝Fsinθ，F ＝Fcosθ 1 2 F 解得F = 1 2 tanθ 故AB错误； C．根据题意可知，船受到的横向阻力与F 等大反向，即等于Fcosθ，故C错误； 2 F sinθ D．根据题意可知，船前进的动力为沿着航向的分力F ，则 1= =tanθ 1 F cosθ 2 解得F ＝F tanθ 1 2 故D正确。 故选：D。 [例题4] （2024•雨花区校级模拟）2023年9月27日，杭州亚运会中国队组合赵焕城/王赛博获得帆船比 赛冠军。图为帆船在静止水面上逆风航行的示意图。风力和船身方向成 135°，风力和帆面成8°，风力在垂 直帆面方向的分力推动帆船逆风行驶，如果风力大小为F，则风力在航行方向的分力为（ ）3 3 4 4 A． Fsin8° B． Fcos8° C． Fsin8° D． Fcos8° 5 5 5 5 【解答】解：由题，结合图可知，风力在垂直于帆面方向上的分力为F′＝Fsin8° 这个分力垂直于帆面，与航行方向之间的夹角为θ＝90°﹣（180°﹣135°﹣8°）＝53° 3 3 所以风力在航行方向上的分力为F″=F'cos53°= F'= Fsin8° 5 5 故A正确，BCD错误 故选：A。 [例题5] （2023•青羊区校级模拟）如图甲所示是斧子砍进木桩时的情境，其横截面如图乙所示，斧子的 剖面可视作顶角为θ的等腰三角形，当施加竖直向下的力F时，则（ ） A．同一斧子，若施加的力F越小，越容易劈开木桩 B．同一斧子，若施加的力F越大，越不容易劈开木桩 C．施加相同的恒力F，θ越大的斧子，越容易劈开木桩 D．施加相同的恒力F，θ越小的斧子，越容易劈开木桩 【解答】解：AB、根据图乙可知，同一斧子，θ一定，F越大，图像放大，故其分力越大，越容易劈开木桩， 故AB错误； CD、参照AB的分析，F一定时，θ越小的斧子，其分力越大，越容易劈开木桩，故C错误，D正确。 故选：D。 考点三 力的合成与分解方法在实际问题中的应用 把力按实际效果分解的一般思路[例题6] （2024•天津模拟）海河九道湾，上上下下一共有74座桥，每一座桥都是天津人生活的一部分。 如图，设某座桥的桥体中有三块相同的钢箱梁1、2、3紧挨着水平排列，受到钢索a、b、c拉力的方向相同， 相邻钢箱梁间的作用力均沿着水平方向，下列说法正确的是（ ） A．钢箱梁3所受合力最大 B．钢索a、b、c上的拉力大小相同 C．钢箱梁1对2的作用力大于2对1的作用力 D．钢索a对钢箱梁1作用力的竖直分力大于钢箱梁1的重力 【解答】解：A：钢箱梁3处于静止状态，根据牛顿第一定律可知钢箱梁3所受合力为0，故A错误； B：假设钢索与竖直方向的夹角为α，则钢索对钢箱梁的拉力F在竖直方向上的分力与钢箱梁的重力相等，即 mg F ＝Fcosα＝mg，则F＝每个 ，钢索a、b、c平行，因此每根钢索的拉力均相等，故B正确； y cosα C：根据牛顿第三定律可知，钢箱梁1对2的作用力与2对1的作用力为相互作用力，大小相等，故C错误； D：因为钢箱梁保持静止，处于受力平衡状态，因此其水平、竖直方向均受力平衡，竖直方向上，钢项链仅受到 重力作用及钢索拉力在竖直方向上的分力作用，因此二力相等，故D错误。 故选：B。 [例题7] （2024•广州一模）如图，港珠澳大桥人工岛建设时，起重机用8根对称分布且长度均为22米的 钢索将直径为22米、质量为5.0×105kg的钢筒匀速吊起，重力加速度取10m/s2，则此过程每根钢索所受到的 拉力大小为（ ） A．6.0×105N B．7.2×105N C．8.8×105N D．1.2×106N 【解答】解：根据几何关系可知，绳索长为22米，圆柱顶面半径为11米，设绳索方向与竖直方向的夹角为θ 11 1 故绳索方向与竖直方向的夹角为cosθ= = 22 2可知θ＝30° 由题意有 8Fcos30°＝mg mg 5×105×10 F= = N=7.2×105N，故B正确，ACD错误。 4√3 4√3 故选：B。 [例题8] （2020•全国模拟）如图所示，重型自卸车装载一巨型石块，当利用液压装置使车厢缓慢倾斜到 一定角度，车厢上的石块就会自动滑下。以下说法正确的是（ ） A．石块没有下滑时，自卸车车厢倾角变大，石块对车厢的压力不变 B．石块没有下滑时，自卸车车厢倾角变大，石块对车厢的摩擦力变大 C．石块开始下滑时，自卸车车厢倾角变大，石块对车厢的作用力变大 D．石块开始下滑时，自卸车车厢倾角变大，石块受到的合力不变 【解答】解：AB、货物处于平衡状态，则有：mgsinθ＝f，N＝mgcosθ，θ增大时，支持力F 逐渐减小，静摩 N 擦力F 先增大。由牛顿第三定律可知，石块对车厢的压力会减小。故A错误，B正确； f CD、石块开始下滑时受力近似平衡，自卸车车厢倾角变大，石块向下做加速运动，可知对车厢的作用力变小， 故CD错误。 故选：B。 [例题9] （多选）（2024•青羊区校级模拟）如图甲所示，野营三脚架由三根对称分布的轻质细杆构成， 炊具与食物的总质量为m，各杆与竖直方向的夹角均为θ。盛取食物时，用光滑铁钩缓慢拉动吊绳使炊具偏 离火堆，如图乙所示。重力加速度为g，下列说法正确的是（ ） A．拉动吊绳的过程中，铁钩对吊绳的作用力沿水平方向 B．拉动吊绳的过程中，铁钩受到吊绳的作用力越来越大 √3 C．烹煮食物时，若θ＝30°，则三根细杆受到地面的摩擦力大小均为 mg 91 D．烹煮食物时，若θ＝30°，则三根细杆对地面的作用力大小均为 mg 3 【解答】解：A、拉动吊绳过程中，炊具与食物受力平衡，故绳子的拉力等于炊具与食物的重力，故大小不变； 用铁钩拉动吊绳过程中，铁钩与吊绳的接触点受到竖直向下的绳子拉力、斜向上的的绳子拉力，以及铁钩对吊 绳的作用力，在拉动吊绳过程中，斜向上的的绳子拉力的方向改变，根据三个共点力平衡可知铁钩对吊绳的作 用力方向沿另外两个力的角平分线的方向，拉力的方向与绳子的合力的方向相反，斜向上，故A错误； B、在拉动吊绳过程中，斜向上的的绳子拉力的方向改变，则绳子的向两个方向的拉力之间的夹角减小，根据平 行四边形定则可知，绳子的两个方向的拉力的合力增大，根据三力平衡的特点可知铁钩受到吊绳的作用力越来 越大，故B正确； C、将三根细杆的力沿竖直方向分解，则有3Fcos30°＝mg mg mg 2√3 可得F= = = mg 3cosθ 3×cos30° 9 2√3 1 √3 在水平方向上根据受力平衡可知烹煮食物时，各杆受到地面的摩擦力f =Fsin30°= mg× = mg，故C 9 2 9 正确； 2√3 D、烹煮食物时，各杆对地面的作用力大小均等于杆受到的吊绳的作用力，为 mg，故D错误。 9 故选：BC。 [例题10] （2023•枣强县校级模拟）如图所示，倾角为30°的斜面上用铰链连接一轻杆a，轻杆a顶 端固定一质量为m的小球（体积可不计），轻绳b跨过斜面顶端的光滑小定滑轮，一端固定在球上，一端用 手拉着，保持小球静让，初始时轻绳b在滑轮左侧的部分水平，杆与斜面垂直，缓慢放绳至轻杆水平的过程 中，斜面始终静止，滑轮右侧的绳与竖直方向夹角始终不变，重力加速度为g，下列说法正确的是（ ） √3 A．初始时轻绳上的拉力大小为 mg 2 B．地面对斜面的摩擦力始终向左且增大 C．铰链对轻杆的支持力一直减小 D．轻绳上的拉力一直减小 【解答】解：A．铰链对轻杆的支持力与滑轮左侧轻绳对球的拉力的合力与小球的重力大小相等、方向相反，初 始时根据几何关系可得： F tan30°= T mg√3 解得：F = mg，故A错误； T 3 BCD．如图甲所示，设球与轻绳的连接点为A，铰链处为B点，过B点作竖直虚线，虚线与绳的交点设为C，画 出力的矢量三角形如图乙所示 根据几何知识可知三角形ABC与力的三角形相似，根据几何关系可得： mg F F = T = N BC AC AB 缓慢放绳过程中，BC减小，AB不变，AC增大，则可得F 增大，F 增大，滑轮右侧轻绳上的拉力在水平方向的 T N 分力一直增大，对整体受力分析可知，地面对斜面的摩擦力始终向左且增大，故B正确，CD错误。 故选：B。 题型1合力的范围 1. （2024•海门区校级学业考试）如图所示，三个共点力F 、F 与F 作用在同一个质点上，其中，F 与 1 2 3 1 F 共线且反向，F 与F 垂直，F ＝6N、F ＝2N、F ＝3N，则质点所受的合力大小是（ ） 2 3 1 1 2 3 A．5N B．4N C．3N D．2N 【解答】解：力F 和F 共线，方向相反，合力为： 1 2 F ＝F ﹣F ＝6N﹣2N＝4N 12 1 2 再将该合力与F 合成，合力为 3 F=√F2 +F2=√42+32N＝5N 12 3 故A正确，BCD错误。 故选：A。 2. （2023秋•南开区期末）三个小朋友在操场上玩游戏，他们沿水平方向用大小分别为150N、200N和 250N的力拉一木箱。若三个小朋友的方位均不确定，则这三个力的合力的最小值和最大值分别为（ ）A．0，600N B．50N，600N C．100N，500N D．200N，500N 【解答】解：当三个力的方向相同时，三个力的合力有最大值，最大值为：F ＝150N+200N+250N＝600N； max 150N、200N两个力合力的最小值为50N、最大值为350N，当这两个力的合力大小为250N，方向与第三个力的方 向相反时，三个力的合力为零，即为最小值。故A正确，BCD错误。 故选：A。 3. （2023秋•孝义市月考）一可视为质点的物体放在光滑水平地面上，现在该物体上施加两个水平方向 的外力F ，F 。已知F ，F 合力的最大值为4N，则当两外力所成的夹角为90°时，物体所受合力的最小值为 1 2 1 2 （ ） A．1N B．2N C．2√2N D．0 【解答】解：已知F ，F 合力的最大值为4N，则 1 2 F +F ＝4N 1 2 当两外力所成的夹角为90°时，合力为 F=√F2+F2 1 2 根据数学方法可知F=√F2+F2≥√2F F 1 2 1 2 当F ＝F ＝2N时，F=√2F F =√2×2×2N=2√2N，故ABD错误，C正确。 1 2 1 2 故选：C。 题型2几种特殊情况的力的合成 4. （2023秋•辽阳期末）在某平面内有作用于同一点的四个力，以力的作用点为坐标原点O，四个力的 方向如图所示，大小分别为F ＝6N，F ＝2N，F ＝3N，F ＝8N。这四个力的合力在（ ） 1 2 3 4 A．第一象限 B．第二象限 C．第三象限 D．第四象限 【解答】解：在x轴上，因为F ＞F ，所以F 、F 合力沿x轴正方向记为F ，在y轴上，因为F ＞F ，所以F 、 1 3 1 3 x 4 2 2 F 合力沿y轴负方向记为F ，再把F 和F 合成，可知这四个力的合力在第四象限。故ABC错误；D正确。 4 y x y 故选：D。5. （2023秋•黄浦区校级期末）如图，在“研究共点力的合成”的实验中，橡皮筋的一端固定在A点， 另一端被两个弹簧测力计拉至O点，此时F 、F 间的夹角为锐角。若保持结点O的位置及F 的方向不变，绕 1 2 1 点O逆时针旋转F ，使两分力的夹角逐渐增大，这一过程中（ ） 2 A．F 一定增大，F 、F 的合力也随之增大 2 1 2 B．F 一定增大，但F 、F 的合力保持不变 2 1 2 C．F 不一定增大，F 、F 的合力也不一定增大 2 1 2 D．F 不一定增大，但F 、F 的合力保持不变 2 1 2 【解答】解：若保持结点O的位置不变，则F 与F 的合力不变，当F 的方向不变，绕点O逆时针旋转F ，使两 1 2 1 2 分力的夹角逐渐增大时，做出平行四边形如图： 可知，当F 方向不变，而绕点O逆时针旋转F ，使两分力的夹角逐渐增大时，F 一直变大，F 先变小后变大． 1 2 1 2 故D正确，ABC错误． 故选：D。 题型3力的分解方法 6. （2023秋•重庆期末）如图所示，一物体在12N的拉力作用下沿水平方向前进，该力与水平方向夹角为30°，若将该力分解为水平向右和竖直向上的两个力，则水平方向的分力大小为（ ） A．10√3N B．6√3N C．4√3N D．6N 【解答】解：该力水平方向的分力大小为 √3 F =Fcos30°=12× N=6√3N x 2 故B正确，ACD错误。 故选：B。 7. （2023秋•天河区期末）木楔的截面为等腰三角形，其顶角为θ，现在木楔背上加一力F，方向如图 所示，木楔两侧产生推力F ，则下列正确的是（ ） N A．θ一定时，F 的大小与F无关 N B．θ一定时，F越小，F 越大 N C．F一定时，θ越大，F 越大 N D．F一定时，θ越小，F 越大 N 【解答】解：选木楔为研究对象，木楔受到的力有：竖直向下的 F和两侧给它的与木楔的斜面垂直的弹力，由 于木楔处于平衡状态，所以两侧给木楔的斜面垂直的弹力与F沿两侧分解的力是大小相等的，力F的分解如图， F θ θ F = 则有：F＝2F cos（90°− ）＝2F sin ，故 N θ； N 2 N 2 2sin 2 AB、若θ一定，F增大则F 增大，F减小则F 减小，故AB错误； N N CD、若F一定，θ增大时F 减小，θ减小时F 增大，故C错误，D正确； N N故选：D。 8. （2023秋•南开区期末）刀、斧，凿等切割工具的刃部叫做劈。如图是斧头劈木头的示意图，劈的纵 截面ABC是一个等腰三角形，使用劈时沿BC中垂面施加一个竖直向下的力F，这个力产生两个作用效果，使 劈的两个侧面推压木柴，把木柴劈开。设劈背BC的宽度为d，劈的侧面AB、AC长为L，劈的侧面推压木柴的 力为F′，不计劈自身重力，则（ ） L A．劈的侧面推压木柴的力F'= F 2d B．仅增大d；F′将增大 C．当d＝L时，F′＝F D．仅减小L，F′将增大 d 【解答】解：设劈的纵截面的三角形顶角为θ，根据几何关系可得sinθ 2 d = = 2 L 2L 将力F按垂直侧面方向进行分解，如图所示 F 2 L 可得F ＝F = = F 1 2 θ d sin 2 则劈的侧面推压木柴的力大小为 L F'＝F = F 1 d 可知仅增大d，F'将减小，仅减小L，F'将减小，当d＝L时，F'＝F，故C正确，ABD错误。 故选：C。题型4力的分解中的多解问题 9. （2023秋•龙凤区校级期中）已知一个力F＝20√3N，可分解为两个分力加F 和F ，已知F 方向与F 1 2 1 夹角为60°，则F 的最小值是（ ） 2 A．5√3N B．10√3N C．10N D．30N 【解答】解：作出力的分解，如图： √3 由图可知F 的最小值是F ＝Fsin60°＝20√3× N＝30N 2 2 2 故ABC错误，D正确； 故选：D。 10. （2023秋•思明区校级期中）将一个大小为20N的已知力F分解成两个力，其中一个分力F 的方向与 1 F的夹角为53°，则当另一个分力F 的大小取以下哪个数值时，力F的分解结果存在两种可能（ ） 2 A．16N B．18N C．20N D．22N 【解答】解：假设F 与力F 垂直，则F ＝12N、F ＝16N，所以当F 小于16N时，此时不能满足题目所给的条件。 2 1 1 2 2 当F ＝16N时，此时不存在两个F 的情况，所以只有当F 大于16N时才能满足题意，并且F 不能大于力F，所 2 2 2 2 以16N＜F ＜20N。故B正确，ACD错误。 2 故选：B。 11. 已知力F的一个分力F 跟F成30°角，则另一个分力F 的大小不可能是（ ） 1 2 √3 √3 A． F B． F C．2F D．3F 4 3 F 【解答】解：根据力的三角形法则可知，当另一个分力与力 F垂直的时候，另一个分力最小，即最小值为 ， 2 √3 所以另一个分力F 的大小不可能是 F，其余选项都有可能，故A正确，BCD错误； 2 4 故选：A。题型5活结与死结绳模型 12. （2023秋•郫都区校级期中）如图甲所示，一个质量为 0.6kg的小环挂在长为0.8m的细线中间，细 线两端分别固定在水平杆上A、B两点，AB间距0.4m，g取10m/s2。 （1）求小环静止时细线上的拉力大小； （2）对小环施加水平向左的拉力作用，使小环静止在A点正下方，如图乙所示，求此时细线上的拉力大小和水 平拉力大小； （3）恢复静止状态，现对小环施加一垂直纸面向外的水平力，使AB与小环组成的平面与竖直方向成30°角静 止，求此时细线上的拉力大小。 【解答】解：（1）细线长为0.8m，AB间距0.4m，则两细线夹角为60°。设细线上的拉力大小F ， T1 则根据平衡条件有：2F cos30°＝mg T1 解得：F =2√3N T1 （2）设细线竖直段长度x ，另一段长度为x ， 1 2 则由题意：x +x ＝0.8m 1 2 由几何关系：x2+0.44=x2 1 2 解得：x ＝0.3m 1 x 0.3 3 设另一段与水平方向夹角为θ，tanθ= 1 = = ，则：θ＝37° 0.4 0.4 4 设此时细线上的拉力大小为F ，水平拉力大小为F，小环竖直方向平衡：F +F sin37°＝mg T2 T2 T2 水平方向平衡：F cos37°＝F T2 求得：F ＝3.75N，F＝3N T2 （3）设此时细线上的拉力大小F ，可得细线上的拉力的合力：F =F =2F cos30°=√3F T3 T合 T合 T3 T3 又：F cos30°＝mg，即：√3F cos30°=mg T合 T3 解得：F ＝4N T3 答：（1）小环静止时细线上的拉力大小为2√3N；（2）此时细线上的拉力大小为3.75N，水平拉力大小为3N； （3）此时细线上的拉力大小为4N。 13. （多选）如图（甲）所示，轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为10kg的物 体，∠ACB＝30°；图（乙）中轻杆HP一端用铰链固定在竖直墙上，另一端P通过轻绳EP拉住，EP与水平方 向也成30°，轻杆的P点用轻绳PQ拉住一个质量也为10kg的物体。g取10m/s2，则（ ） A．轻绳AC段的张力F 的大小为100N AC B．轻绳EP的张力F 的大小为200N EP C．横梁BC对C端的支持力大小为100N，方向水平向右 D．轻杆HP对P端的支持力大小为100√3N，方向水平向右 【解答】解：AB、题图甲和乙中的两个物体M 、M 都处于平衡状态，根据平衡条件可判断，与物体相连的细绳 1 2 拉力大小等于物体的重力。分别取C点和P点为研究对象，进行受力分析如图甲和乙所示。 图甲中轻绳AD跨过定滑轮拉住质量为M 的物体，物体处于平衡状态，绳AC段的拉力F ＝F ＝M g＝10×10N＝ 1 AC CD 1 100N； 图乙中由F sin30°＝M g EP 2 得：F ＝2M g＝2×10×10N＝200N，故AB正确； EP 2 C、横梁BC对C端的支持力大小为F ＝F ＝F ＝100N，方向如图甲所示，不是水平向右，故C错误； C AC CD √3 D、轻杆HP对P端的支持力大小为F ＝F cos30°＝200× N＝100√3N，方向水平向右，故D正确。 P EP 2 故选：ABD。 14. （多选）如图所示，BC是一轻杆，可绕C点转动，AB是一连接在墙壁和杆上的轻绳，在杆的B点悬 挂一个定滑轮，人用它匀速地提起重物，重物质量为30kg，人的质量为50kg。（g取10m/s2绳子和滑轮的质 量、绳子和滑轮的摩擦及杆的自重忽略不计）下列说法正确的是（ ）A．此时人对地面的压力大小是200N B．定滑轮对B点竖直向下的拉力大小是300N C．AB绳的拉力大小为600N D．支架的斜杆BC所受的力大小是1200N 【解答】解：A、重物匀速上升，T＝mg＝30×10N＝300N，人受重力G、绳子拉力T、地面支持力N，由平衡条 件得：N＝G﹣T＝50×10﹣30×10N＝200N，据牛顿第三定律，地面对人的支持力大小等于人对地面的压力大小， 则人对地面的压力为200N．故A正确； B、B点受到向下的拉力为F ＝2T＝2×300N＝600N，故B错误； B 2T 2×300 = = N=1200N C、B点受力如图：因杆可绕C点转动，所以杆BC对B点作用力沿CB方向F sin30° 1 BC 2 2T 2×300 = = N= 水平绳AB所受的拉力：F tan30° √3 600 √3N，故C错误，D正确； AB 3 故选：AD。 题型6动杆和定杆模型 15. 如图所示，一水平轻杆AB可绕过A点的水平光滑轴转动，B端挂一重物，并用长度可改变的细线挂 于墙上的C点．若保持轻杆AB处于水平状态，则改变细线BC的长度将C点沿墙上移的过程中，轻杆B端所受 的力（ ）A．逐渐减小 B．逐渐增大 C．大小不变 D．先减小后增大 【解答】解：B点受重物的拉力、细线的拉力、杆的支持力，三力平衡，根据平衡条件，可以将三个力平移到 一个矢量三角形中，如图所示： 细线拉力与水平方向的夹角逐渐增加，故细线的拉力T与杆的支持力N均是逐渐减小， 题目问的是B点受到的力，是逐渐减小； 故A正确，BCD错误； 故选：A。 16. （多选）如图所示的四个图中，AB、BC均为轻质杆，各图中杆的A、C端都通过铰链与墙连接，两杆 都在B处由铰链连接，且系统均处于静止状态。现用等长的轻绳来代替轻杆，能保持平衡的是（ ） A．图中的AB杆可以用轻绳代替的有甲、乙、丙 B．图中的AB杆可以用轻绳代替的有甲、丙、丁 C．图中的BC杆可以用轻绳代替的有丙 D．图中的BC杆可以用轻绳代替的有甲、丙 【解答】解：根据（轻）绳子只能提供拉力的特点和对B点受力分析结合平衡条件可知图甲、乙、丁中的BC不 能用绳子代替；因轻杆通过铰链连接，说明杆产生弹力方向一定沿着杆的方向，则甲、丙、丁中 AB可以用绳子 代替，而乙不行，故AD错误BC正确。 故选：BC。 17. 如图（a）所示，轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为m 的物体。∠ACB＝ 130°；图（b）中轻杆HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG与水平方向也成30°， 轻杆的G点用细绳GF拉住一个质量为m 的物体，则下列说法中正确的是（ ） 2 m A．图（a）中BC杆对滑轮的作用力为 1g 2 B．图（b）中HG杆受到的作用力为m g 2 C．细绳AC段的张力T 与细绳EG的张力T 之比为1：1 AC EG m 1 D．细绳AC段的张力T 与细绳EG的张力T 之比为 AC EG 2m 2 【解答】解：A、图（a）中，两段绳的拉力都是G，互成120°，因此合力大小是m g，根据共点力平衡，BC杆 1 对滑轮的作用力大小也是m g，（方向与竖直向上方向成60°，斜向右上方），故A错误； 1 B、图（b）中，以G点为研究对象，分析受力情况，如图，由平衡条件得，T tan30°＝m g，得T =√3m g， HG 2 HG 2 即HG杆的作用力为√3m g，故B错误； 2 TAC m = 1 C、D图（a）中绳AC段的拉力T ＝m g；图（b）中由于T sin 30°＝m g，得T ＝2m g，解得： ， AC 1 EG 2 EG 2 TEG 2m 2 故C错误，D正确。 故选：D。第 5 讲 受力分析 共点力的平衡 1、掌握受力分析的基本方法和规律，并能对多个物体进行受力分析 2、能利用所学知识解决静态平衡问题的方法处理相关问题。考点一 整体与隔离法的应用 1．受力分析的定义 把指定物体(研究对象)在特定的物理环境中受到的所有外力都找出来，并画出受力示意图，这个过程就是受力分析． 2．受力分析的一般顺序 先分析场力(重力、电场力、磁场力)，再分析接触力(弹力、摩擦力)，最后分析其他力． [例题1] （2024•丰台区二模）如图所示，水平地面上放置一个质量为 10kg、倾角为37°的斜面体。一个 质量为5kg的箱子在平行于斜面的拉力F作用下，沿斜面体匀速上滑，斜面体保持静止。已知箱子与斜面间 的动摩擦因数为0.25，重力加速度g取10m/s2，sin37°＝0.6，cos37°＝0.8。下列说法正确的是（ ） A．箱子对斜面体压力的大小为30N B．拉力F的大小为10N C．斜面体对地面压力的大小为150N D．地面给斜面体的摩擦力大小为32N 【解答】解：AB、对箱子受力分析，如图： 由平衡条件得：F＝f+mgsin37° N＝mgcos37° f＝μN 代入数据联立解得：N＝40N f＝10N F＝40N 由牛顿第三定律可知，箱子对斜面体压力的大小为40N，故AB错误；CD、对斜面体和箱子整体受力分析，如图 由平衡条件得：Fsin37°+N′＝（M+m）g Fcos37°＝f′ 代入数据联立解得：f′＝32N N′＝126N 由牛顿第三定律得，斜面体对地面压力大小为126N，故C错误，D正确。 故选：D。 [例题2] （2024•琼山区校级模拟）如图所示，（本资料来自于公众号：屋里学家）质量为M的光滑半圆 柱体紧靠墙根放置，质量为m的小球由长度为L的细线悬挂于竖直墙壁上的A点，静止在半圆柱体上，A点 距离地面的高度为L，细线与竖直方向夹角为θ。已知半圆柱体的半径可变化（质量不变），小球可视为质点， 重力加速度为g，不计一切摩擦，下列说法正确的是（ ） √3 A．当θ＝60°时，细线对小球的拉力大小为 mg 2 1 B．当θ＝60°时，半圆柱体对小球的支持力大小为 mg 2 C．半圆柱体受到水平地面的弹力大小为Mg+mgsin2θ D．半圆柱体受到竖直墙壁的弹力最大值为mg 【解答】解：AB、对小球进行受力分析如图所示 由几何关系可知α＝θ 根据小球受力平衡，可得：N＝mgsinθ，T＝mgcosθ√3 1 代入数据解得：N= mg，T= mg，故AB错误； 2 2 CD、对小球和半圆柱体整体进行受力分析，整体受地面的支持力F ，墙壁的弹力F，细线的拉力T，重力 N （m+M）g，整体受力平衡，则在竖直方向上有F +Tcosθ＝（m+M）g N 水平方向上有F＝Tsinθ 代入解得：F =Mg+mgsin2θ N 1 F= mgsin2θ 2 1 则当θ＝45°时，F最大，最大为 mg，故C正确，D错误。 2 故选：C。 [例题3] （2024•鹿城区校级模拟）俗称书籍整理神器的“铁书立”是一种用来支撑书籍以达到使书籍平 稳站立效果的物品，如图所示．现在简化为如下示意图，水平桌面上有一质量为M的静止的“铁书立”，刚 好静止摆放了两本书A和B，由此可知（ ） A．桌面对A书有向上的弹力 B．B书受到的合力为0 C．B书与“铁书立”之间可以无摩擦 D．“铁书立”对桌面的压力为Mg 【解答】解：A、由题图甲知，A书与桌面没有接触，则桌面对A书不会有弹力，故A错误； B、B书处于静止状态，所以合力为0，故B正确； C、对B书受力分析知，“铁书立”对B书有向上的弹力，A书对B书有向右的弹力，又B书处于静止状态， 则B书有相对“铁书立”向右运动的趋势，所以水平方向“铁书立”对B书有向左的摩擦力，故C错误； D、选整体为研究对象分析知，“铁书立”对桌面的压力大于Mg，故D错误； 故选：B。 考点二 处理平衡问题常用的“三种”方法处理平衡问题的常用方法 1．合成法：物体受三个共点力的作用而平衡，则任意两个力的合力一定与第三个力大小相等、方向相反．2．分解法：物体受三个共点力的作用而平衡，将某一个力按力的效果分解，则其分力和其他两个力满足平衡条件． 3．正交分解法：物体受到三个或三个以上力的作用而平衡，将物体所受的力分解为相互垂直的两组，每组力都满 足平衡条件． 1 [例题4] （2024•麦积区二模）如图所示，粗糙水平地面上放有横截面为 圆的柱状物体A，A与墙面之 4 间放有表面光滑的圆柱形物体B，A、B均保持静止。若将A向左移动少许，下列说法正确的是（ ） A．地面对A的支持力不变 B．地面对A的摩擦力不变 C．墙对B的作用力不变 D．B对A的支持力不变 【解答】如图，A的重力为G ，B的重力为G ，地面对A的支持力为F，地面对A的摩擦力为f，B对A的作 A B 用力为F ，与水平方向的夹角为θ，A对B的作用力为F ，与水平方向的夹角为θ，墙面对B的作用力为 BA AB F 。 B 解：A.由整体分析可知，A、B保持静止时地面对A的支持力等于A与B的重力之和，将A向左移动少许， A、B仍将保持静止，因此地面对A的支持力不变，故A正确； B.如图，对A进行受力分析可知f＝F cosθ，又有F ＝F ，且F sinθ＝G ，因此有 BA BA AB AB B cosθ f＝G Bsinθ G B 将A向左移动，θ增大，f减小，故B错误； sinθ C.由整体分析可知，墙面对B的作用力等于地面对A的摩擦力，已知地面对A的摩擦力减小，故C错误； D.B对A的作用力 G F = B BA sinθθ增大，F 减小，故D错误。 BA 故选：A。 [例题5] （2024•樟树市模拟）2023年12月4日，陇东～山东±800千伏特高压直流输电工程（甘肃段） 铁塔组立首基试点在庆阳市西峰区什社乡N0003号塔举行，标志着该工程正式进入铁塔组立阶段。如图所示 为相邻铁塔间某根输电线的示意图，A、B两点分别为铁塔与输电线的连接点且等高，C点为该段输电线的最 低点，C点切向方向水平，输电线质量分布均匀，输电线两端的切线与竖直方向的夹角 θ ＝θ ＝60°，AB间 A B 输电线总质量为2m，重力加速度为g，下列说法正确的是（ ） A．左铁塔A处对输电导线的拉力大小为2√3mg B．C处输电导线的张力大小为√3mg C．从A点到C点输电线上张力大小一直增加 D．由于热胀冷缩，冬季输电线与竖直方向的夹角增加，输电线两端的弹力大小减少 【解答】解：A.如图所示，因为输电线路保持静止，对输电线路进行整体受力分析可知，水平竖直方向所受合 力均为0，则有F cos60°+F cos60°＝2mg，F cos30°＝F cos30°，联立可得F ＝2mg，故A错误； A B A B A B.将AC段看作一个整体，进行受力分析可知AC段受力F 作用，自身的重力以及C点因为输电线的张力而存 A 在的向右的拉力F ，因为AC段保持静止，因此有FAcos30°＝F ，F =√3mg，故B正确； C C C C.在AC间任取一点D，将AD看错整体进行受力分析可知，受到拉力F 的作用，自身重力，D点输电线路上 A √3mg 的张力对AD的拉力作用F ，假设F 与竖直方向的夹角为α，则有F sin60°＝F sinα=√3mg，因此F = D D A D D sinα ，结合图象可知，从A点到C点，α逐渐增大，因此F 逐渐减小，故C错误； D D.由于热胀冷缩，到冬季时θ角增大，对输电线路整体受力分析可知，F cosθ+F cosθ＝2mg，因为θ增大，因 A B 此F 增大，故D错误。 A 故选：B。 [例题6] （2024•南充模拟）如图甲是一种常见的持球动作，用手臂挤压篮球，将篮球压在身侧。为了方便问题研究，将该场景模型化为如图乙，若增加手臂对篮球的压力，篮球依旧保持静止，则下列说法正确的 是（ ） A．篮球受到的合力增大 B．篮球对人的静摩擦力方向竖直向上 C．人对篮球的作用力的方向竖直向上 D．手臂对篮球的压力是由于篮球发生形变而产生的 【解答】解：AC、篮球受到重力和人对篮球的作用力下保持静止状态，根据力的平衡条件可知，篮球的重力与 人对蓝球的作用力大小相等方向相反，即人对篮球的作用力的方向竖直向上，篮球受到的合力不变，A错误， C正确； B、篮球对人的静摩擦力在篮球与人的两个接触面间都有，根据受力平衡，两个摩擦力的向上的合力等于重力 与压力的分力，根据相互作用力，人受到篮球的摩擦力不是竖直向上的，故B错误； D、根据弹力产生的特点，手臂对篮球的压力是由于手臂发生形变而产生的，D错误。 故选：C。 考点三 动态平衡问题的处理技巧 1．动态平衡：是指平衡问题中的一部分是变力，是动态力，力的大小和方向均要发生变化，所以叫动态平衡，这 是力平衡问题中的一类难题． 2．基本思路：化“动”为“静”，“静”中求“动”． 3．基本方法：图解法和解析法． [例题7] （2024•淮安模拟）我们常用支架与底板垂直的两轮手推车搬运货物。如图甲所示，将质量为 m 的货物平放在手推车底板上，此时底板水平；缓慢压下把手直至底板与水平面间的夹角为 60°。不计货物与支 架及底板间的摩擦，重力加速度为g，下列说法正确的是（ ）√3mg A．当底板与水平面间的夹角为30°时，底板对货物的支持力为 2 √3mg B．当底板与水平面间的夹角为30°时，支架对货物的支持力为 2 C．压下把手的过程中，底板对货物的支持力一直增大 D．压下把手的过程中，支架对货物的支持力一直减小 【解答】解：AB、当底板与水平面间的夹角为30°时，对货物受力分析，两个弹力的合力与重力等大反向，如 下图所受： 1 mg 两个弹力N 与N 垂直，由平衡条件可得支架对货物的支持力：N =mgsin30°=mg× = 1 2 1 2 2 √3 √3mg 底板对货物的支持力：N =mgcos30°=mg× = ，故A正确，B错误； 2 2 2 CD、压下把手的过程中，两个弹力的夹角始终是90°，货物的受力情况如下图所示： 由图可知，底板对货物的支持力N 一直减小，支架对货物的支持力N 一直增大，故CD错误。 1 2 故选：A。 [例题8] （2024•渝中区校级模拟）如图，一根绝缘的光滑水平横杆上套有质量均为 m的A、B两个小环， 两环上都带有正电荷，系在两环上的等长细绳拴住质量为M的物块处于静止状态，某时刻开始环上电荷量缓 慢减少，则（ ）A．单根细绳对物块的拉力始终不变 B．两细绳对物块的合力变大 C．杆对A环的作用力保持不变 D．两环间距等于绳长时，单根细绳拉力大小等于Mg 【解答】解：A、对左侧圆环受力分析 当电荷减小后，库仑力会减小，所以水平方向上为了保持受力平衡，绳子上的拉力也会减小，故A错误； B、两个细绳的拉力组成的合力始终与物块的重力相平衡，所以合力始终不变，故B错误； C、对物块受力分析，如上图所示 Mg 对物块而言竖直方向上2T'cosθ＝Mg，解得T'= 2cosθ Mg 对圆环而言，由于T＝T'，所以F ＝mg+Tcosθ，得到F ＝mg+ ，所以支持力不变，故C正确； N N 2 √3Mg D、当两环间距等于绳长时，构成一个等边三角形，即θ＝30°，所以T'= ，故D错误； 3 故选：C。 [例题9] （2024•郫都区校级二模）一物块放置在固定斜面上，对物块施加一水平力F，保持该力的大小 不变，在将该作用力沿水平方向逆时针缓慢转动至竖直方向的过程中，物块始终静止在斜面上，如图所示。 则该过程中（ ） A．斜面对物块的摩擦力逐渐减小 B．斜面对物块的支持力先减小后增大 C．斜面对物块的作用力先减小后增大D．斜面对物块的作用力一直减小 【解答】解：对物块受力分析，如图所示： AB、受重力、拉力、支持力和摩擦力，设拉力与斜面间的夹角为θ，若摩擦力开始向下，根据受力平衡可得： f+mgsinα＝Fcosθ，当F逆时针转动时θ减小，所以摩擦力减小，若摩擦力开始向上，当 θ减小时，摩擦力减小， 故AB错误； CD、斜面体对物块的作用力包括摩擦力和支持力，当F逆时针转动时，F与mg的合力减小，根据受力平衡可 得，f与F′的合力也减小，所以斜面对物块的作用力减小，故C错误，D正确。 故选：D。 考点四 平衡中的临界与极值问题 1．临界问题 当某物理量变化时，会引起其他几个物理量的变化，从而使物体所处的平衡状态“恰好出现”或“恰好不出现”， 在问题的描述中常用“刚好”、“刚能”、“恰好”等语言叙述． 常见的临界状态有： (1)两接触物体脱离与不脱离的临界条件是相互作用力为0(主要体现为两物体间的弹力为0)． (2)绳子断与不断的临界条件为绳中的张力达到最大值；绳子绷紧与松驰的临界条件为绳中的张力为0. (3)存在摩擦力作用的两物体间发生相对滑动或相对静止的临界条件为静摩擦力达到最大． 研究的基本思维方法：假设推理法． 2．极值问题 平衡物体的极值，一般指在力的变化过程中的最大值和最小值问题．一般用图解法或解析法进行分析． [例题10]（2024•龙岗区校级三模）如图所示，在竖直墙壁上固定水平轻杆OB，B为铰链装置，OA为轻 质细绳且与水平方向夹角θ＝30°，小球质量为m，通过轻绳系于O点，初始时整个装置处于静止状态，现保 证O点位置不变，逐渐减小绳OA的长度，使绳的上端由A点缓慢移动至C点。已知重力加速度为g，不计 所有摩擦，则下列说法正确的是（ ）A．初始时OA绳的拉力大小为√3mg B．移动过程中OA绳的拉力大小逐渐增大 C．移动过程中OB杆的弹力逐渐减小 D．最终OA绳的拉力大小减小至0 【解答】解：A、初始时整个装置处于静止状态，设OA绳的拉力大小为F ，竖直方向上，根据平衡条件得： T mg＝F sin30°，解得：F ＝2mg，故A错误； T T BD、根据平衡条件，竖直方向上可得mg＝F sinθ T mg 则得F = T sinθ 绳的上端由A点缓慢移动至C点，θ增大，sinθ增大，则F 逐渐减小直至mg，故BD错误； T mg C、水平方向上，根据平衡条件得：F = NB tanθ 绳的上端由A点缓慢移动至C点，θ增大，tanθ增大，则F 逐渐减小，故C正确。 NB 故选：C。 [例题11] （2022•聊城模拟）歼—20战斗机安装了我国自主研制的矢量发动机，能够在不改变飞机飞行方 向的情况下，通过转动尾喷口方向改变推力的方向，使战斗机获得很多优异的飞行性能．已知在歼—20战斗 机沿水平方向超音速匀速巡航时升阻比（垂直机身向上的升力和平行机身向后的阻力之比）为k，飞机的重力 为G．能使飞机实现水平匀速巡航模式的最小推力是（ ） G G G A． B． C． D．G 1+k2 k √1+k2 【解答】解：飞机受到重力G、发动机推力F 、升力F 和空气阻力f，重力的方向竖直向下，升力F 的方向竖 1 2 2 直向上，空气阻力f的方向与F 垂直，如图 2 歼—20战斗机沿水平方向超音速匀速巡航，则有水平方向F ＝f x竖直方向F +F ＝G 2 y 其中F ＝kf 2 解得F ＝G﹣kf y 则F2=F2+F2=f2+G2﹣2Gkf+k2f2 1 x y kG 结合数学知识可知F2表达式为开口向上，对称轴为f＝Gk的抛物线，即当f = 时取得最小值，将其代入F2 1 k2+1 1 表达式， G = 解得F ，故ABD错误，C正确 m √1+k2 故选：C。 [例题12]如图所示，质量为2.5m的物体A放在倾角为α＝30°的固定斜面体上，一平行于斜面的轻绳跨过 光滑定滑轮一端与物体A连接，另一端与一竖直轻弹簧相连，弹簧下端悬挂一质量为 m的砝码盘B，整个系 统处于静止状态。现将质量为m的砝码轻轻放在B盘中，二者开始运动。B在运动过程中始终未着地，已知 最大静摩擦力等于滑动摩擦力。轻绳不可伸长，弹簧始终在弹性限度内，要使物体A始终保持静止状态，A 和斜面体之间的动摩擦因数的最小值为（ ） √3 √3 4√3 7√3 A． B． C． D． 3 15 15 15 【解答】解：放砝码之前，B保持静止合力为零，根据二力平衡得弹簧弹力为F ＝mg； 1 放砝码之后，砝码盘和砝码作为整体做简谐运动，且此时的回复力为最大值F ＝2mg﹣F ＝2mg﹣mg＝mg，方 m 1向竖直向下，简谐运动的位移为向上最大值； 当整体合力为零时即为平衡位置，此时弹簧弹力F ＝2mg，根据简谐运动的对称性可知，当简谐运动的位移为 2 向下最大值时，设弹簧弹力为F ，回复力方向向上且为最大值F ＝F ﹣2mg＝mg，得F ＝3mg，方向竖直向上； 3 m 3 3 此时对物体A受力分析，绳子拉力最大为T＝F ＝3mg，动摩擦因数最小值满足T＝2.5mgsin30°+μ（2.5mg） 3 cos30° 7√3 代入数据解得μ= ，故D正确，ABC错误。 15 故选：D。 [例题13]（2024•长春一模）如图，质量为m的光滑球体夹在竖直墙壁和斜面体之间，斜面体质量为 2m，倾角θ＝37°，设斜面体与地面间的最大静摩擦力等于滑动摩擦力，若斜面体恰好不滑动，则斜面体与水 平地面间的动摩擦因数μ为（sin37°＝0.6，cos37°＝0.8）（ ） 1 3 2 4 A．μ= B．μ= C．μ= D．μ= 4 8 3 9 【解答】解：设摩擦因数为μ，对整体受力分析如图所示， 根据平衡条件可求，地面对整体的支持力：F ＝3mg N 地面对斜面的静摩擦力等于墙对小球的弹力：f＝F 1 由于斜面恰好不滑动，所以斜面体与地面间的静摩擦力到达最大：f ＝μF ＝μ（m+2m）g m N 对球体受力分析如图所示， 根据平衡条件可得：F ＝mgtan37° 1 由以上可知斜面体与地面间的最大静摩擦力：f ＝F ＝mgtan37° m 11 联立以上解得：μ= 4 故选：A。 题型1整体法与隔离法 1. （2023•绵阳模拟）新春佳节，大街小巷总会挂起象征喜庆的中国红灯笼。如图所示，由4根等长轻 质细绳AB、BC、CD、DE悬挂起3个质量相等的灯笼，绳两端的结点A、E等高，AB绳与竖直方向的夹角 为α，绳中张力大小为F ；BC绳与竖直方向的夹角为β，绳中张力大小为F ，则（ ） 1 2 A．α可能等于β B．α可能大于β C．F ＞3F D．F ＜3F 1 2 1 2 【解答】解：由对称性可知AB绳和DE绳张力大小相等，大小为F 。对三个灯笼的整体分析，由受力平衡可 1 得：在竖直方向有：2F cosα＝3mg 1 对结点B受力分析，由受力平衡可得：F sinα＝F sinβ 1 2 F cosα＝mg+F cosβ 1 2 联立解得：3tanα＝tanβ 3mg mg F = 、F = 1 2cosα 2 2cosβ AB、由3tanα＝tanβ，可知α＜β，故AB错误； 3mg mg CD、由F = 、F = 1 2cosα 2 2cosβ F 3cosβ 可知 1= F cosα 2 又α＜β，得：cosα＞cosβ 所以可得：F ＜3F 1 3故C错误，D正确。 故选：D。 2. （2023•玉林三模）如图所示，质量为m的圆环A，跨过定滑轮的细绳一端系在圆环A上，另一端系 一物块B。细绳对圆环A的拉力方向水平向左。设最大静摩擦力等于滑动摩擦力，圆环 A与固定直杆间动摩 擦因数 μ＝0.5，直杆倾角θ＝37°，cos37°＝0.8，要保证 A不向上滑动，所悬挂的物块 B 质量不能超过 （ ） 5 5 4 A．2m B． m C． m D． m 3 4 3 【解答】解：对物体B，由平衡条件可得绳子拉力为：T＝m g B 对圆环A受力分析，如图 当圆环刚要上滑时，由平衡条件可得沿杆的方向，有：Tcosθ＝mgsinθ+f m 垂直于杆的方向，有：N＝Tsinθ+mgcosθ 又f ＝μN m 联立解得m ＝2m B 即悬挂的物块B质量不能超过2m，BCD错误，A正确。 故选：A。 3. （2024•浙江模拟）图甲是传统民居建筑材料瓦片，相同的质量为m的瓦片紧靠在一起静止竖直叠放 在水平地面上如图乙所示。下方瓦片的受力点均在其顶端，则瓦片（ ）A．4右端对地面的压力比左端的大 B．5右端受到的支持力是2右端受到支持力的2倍 C．4顶端受到的压力大小为mg 5 D．5左端对地面的压力为 mg 4 1 【解答】解：A、1对2的压力为 mg 2 1 1 3 2对4的压力为F = ×（ mg+mg）= mg 24 2 2 4 1 1 7 4对地面的压力F = ×（ mg+F ），解得 mg，故A错误； 4 2 2 24 8 3 BD、2的右端所受支持力为F = mg 2 4 1 1 5 5的右端所受的支持力为F = ×（ mg+2F ），解得F = mg，故D正确，B错误； 5 2 2 2 5 4 3 C、4的顶端受到的压力大小为F＝F = mg，故C错误。 2 4 故选：D。 4. （2024•深圳二模）如图为我国传统豆腐制作流程中用到的过滤器，正方形纱布的四角用细绳系在两 根等长的、相互垂直的水平木杆两端，再通过木杆中心转轴静止悬挂在空中。豆浆过滤完，纱布与豆渣的总 质量为m，细绳与竖直方向的夹角始终为θ。下列说法正确的是（ ） mg A．此时每根细绳受到的拉力为 4cosθ mg B．此时每根细绳受到的拉力为 4C．豆浆从纱布流出过程中，忽略纱布的拉伸形变，细绳受到的拉力变大 D．豆浆从纱布流出过程中，纱布中豆浆和豆渣整体的重心不变 【解答】解：AB、对纱布和豆渣受力分析，如图所示： 1 1 设每根绳的拉力为F，根据受力平衡，每根绳的拉力在竖直方向的分力等于 G，即：Fcosθ= mg 4 4 mg 解得：F= ，故A正确，B错误； 4cosθ mg CD、豆浆流出过程中整体的质量减少，根据：F= ，可知F减小；豆浆流出过程中根据整体质量的变化 4cosθ 可以判断，整体的重心先向下移，当豆浆流出到一定程度后，重心又会上移，故CD错误。 故选：A。 题型2合成法处理物体静态平衡问题 5. （2024•佛山二模）图甲是一质量分布均匀的长方体药箱，按图乙所示的方式用轻绳悬挂在墙面一光 滑的钉子P上，图丙为右视图。已知药箱长ab＝30cm，质量m＝0.4kg，药箱上表面到钉子的距离h＝10cm， 轻绳总长度L＝50cm，两端分别系在O、O′两点，O是ad的中点，O'是bc的中点，不计药箱与墙壁之间的摩 擦力，g取10m/s2，则轻绳上拉力大小为（ ）A．4N B．5N C．8N D．10 N DP ℎ 【解答】解：根据几何关系可知PO＝25cm，另OO′的中点为D，则2T × =mg OP Dp 代入数据解得T＝5N，故B正确，ACD错误。 故选：B。 6. （2024•正定县校级三模）在吊运表面平整的重型板材（混凝土预制板、厚钢板）时，如因吊绳无处 钩挂而遇到困难，可用一根钢丝绳将板拦腰捆起（不必捆的很紧），用两个吊钩勾住绳圈长边的中点起吊 （如图所示），若钢丝绳与板材之间的动摩擦因数为μ，为了满足安全起吊（不考虑钢丝绳断裂），需要满足 的条件是（ ） A．tanα＞μ B．tanα＜μ C．sinα＞μ D．sinα＜μ 【解答】解：要起吊重物，只需满足绳子张力T的竖直分量小于钢丝绳与板材之间的最大静摩擦力，如图所示 即μTcosα＞Tsinα 化简可得tanα＜μ 故B正确，ACD错误。 故选：B。 题型3正交分解法处理物体静态平衡问题 7. （2024•长沙模拟）如图所示，固定的倾角为37°的粗糙斜面上放置一长方体物块，现用一大小等于 物块重力，方向与斜面成37°角斜向下的推力推动物块（力的作用线在斜面上的投影与斜面底边平行），物块 在斜面上恰好做匀速运动。则物块与斜面间的动摩擦因数为（sin37°＝0.6，cos37°＝0.8）（ ）3 5 5 5 A． B． C． D． 4 4 6 7 【解答】解：设物块的质量为m，对物块受力分析，根据共点力平衡条件可知 Fsin37°+mgcos37°＝N √(Fcos37°) 2+(mgsin37°) 2=f 根据摩擦力的公式有f＝μN 5 解得μ= 7 故ABC错误，D正确； 故选：D。 8. （2024•兴宁区二模）如图（a）所示，刷油漆的使用的滚筒刷，既可以刷天花板，也可以刷竖直墙面 和水平地面，某同学为了研究其运动过程中的受力情况，将刷天花板时的过程简化为图（b），质量为m的物 体在外力F的作用下沿水平方向做匀速直线运动，F与水平方向的夹角为θ，若保持F大小不变，F与水平方 向的夹角仍为θ，物体与天花板和水平地面之间的动摩擦因数相同，建立如图（c）所示模型进行分析，假设 最大静摩擦力等于滑动摩擦力，关于图（b）和图（c）中物体所受摩擦力，下列说法正确的是（ ） A．图（b）中物体所受摩擦力大 B．图（c）中物体所受摩擦力大 C．图（b）和图（c）中物体所受摩擦力一样大 D．以上三种情况都有可能 【解答】解：对图（b）受力分析 Fcosθ＝fFsinθ＝N+mg f＝μN 对图（c）受力分析 Fcosθ＝f 对于图（b）和（c）都有Fcosθ＝f 所以图（b）和（c）摩擦力一样大 故C正确，ABD错误。 故选：C。 题型4力的三角形法处理物体静态平衡问题 9. （2024•雨花区校级模拟）随着工作压力的增大以及生活水平的提高，越来越多的人选择在假期出行 旅游放松。若车厢上放置一与地板成θ角的木板，木板上静置一木块。某段时间内，木块随车厢一起斜向上 做加速度为a的匀加速运动。已知缆绳与水平方向夹角也为θ。若木板与车厢底板夹角缓慢增大稍许，木块、 木板与车厢始终保持相对静止，则关于木块对木板的压力 F 和木块对木板的摩擦F，下列说法正确的是（ N f ） A．F 减小，F 减小 B．F 增大，F 增大 N f N f C．F 减小，F 增大 D．F 增大，F 减小 N f N f 【解答】解：对木块受力分析如图甲所示，因为车厢沿缆绳斜向上加速运动，所以三个力的合力沿缆绳斜向右 上，因此支持力与静摩擦合力斜向右上，因为木块质量和加速度均不变，故三个力的合力不变。 又木块重力不变，则支持力与静摩擦合力不变。木板与底板夹角缓慢增大稍许，画出木块的受力分析图，如图 乙所示F 减小，F 增大。 N f 故ABD错误，C正确； 故选：C。 10. （2024•贵州模拟）如图所示，光滑斜面上小球被轻绳拴住悬挂在天花板上，斜面置于粗糙水平地面 上，整个装置处于静止状态。已知细绳与竖直方向夹角为θ，斜面倾角为α＝45°（θ＜α），现用力向右缓慢 推斜面（推力在图中未画出），当细绳与竖直方向的夹角θ＝α时，撤去推力。则下列说法正确的是（ ） A．缓慢推动斜面时，斜面对小球的支持力保持不变 B．缓慢推动斜面时，细绳对小球的拉力大小保持不变 C．θ＝α时，地面对斜面体的摩擦力水平向左 D．θ＝α时，细绳对小球的拉力大小等于斜面对小球的支持力大小 【解答】解：AB、对小球受力分析，如图所示： 由图可知，缓慢推动斜面时，斜面对小球的支持力仅其方向保持不变，细绳对小球的拉力大小及方向均发生变 化，故AB错误； C、θ＝α时，根据受力平衡可知，地面对斜面体的摩擦力水平向右，故C错误； D、θ＝α时，由矢量三角形法则可知细绳对小球的拉力大小等于斜面对小球的支持力大小，故D正确。 故选：D。11. （2023•安徽模拟）筷子是中华饮食文化的标志之一。如图所示，用筷子夹质量为 m的小球处于静止， 筷子均在竖直平面内，且筷子与竖直方向的夹角均为θ。忽略小球与筷子之间的摩擦，重力加速度为g。下列 说法正确的是（ ） A．筷子对小球的合力大于重力 mg B．筷子的弹力大小均为N= 2cosθ C．保持左侧筷子固定不动，右侧筷子缓慢变为竖直，左、右筷子的弹力均逐渐变大 D．保持左侧筷子固定不动，右侧筷子缓慢变为竖直，左、右筷子的弹力均逐渐变小 【解答】解：A、用筷子夹着小球在竖直平面内处于静止状态，根据平衡条件可知，筷子对小球的合力与小球 的重力等大反向，故A错误； B、对小球受力分析，如图： mg 由几何关系可知，筷子对小球的弹力大小为N= 2sinθ 故B错误； CD、保持左侧筷子固定不动，右侧筷子缓慢变为竖直，在右边筷子转到竖直方向的过程中，左边筷子对小球弹 力N 的方向始终垂直于筷子，方向不变，而小球自身的重力是一个恒力，由此可以做出在动态平衡过程中力的 1 矢量三角形如下图所示 当两根筷子与竖直方向夹角都为θ时，三力构成的矢量三角为等腰三角形，在右边的筷子转到竖直方向时，三 个力的矢量构成一个直角三角形，易得，在右边筷子转到竖直的过程中，两筷子对小球的弹力都在增大，故C 正确，D错误。 故选：C。 12. （2023•湖南二模）如图所示，倾角为θ＝30°、AB面光滑的斜面体放在水平地面上，一个重为 G的 小球在弹簧秤的水平拉力F作用下静止在斜面上。现沿逆时针方向缓慢转动弹簧秤，直到弹簧秤的示数等于初始值，在此过程中，小球与斜面体始终处于静止状态。下列说法正确的是（ ） A．力F先变大后变小 B．地面对斜面体的支持力一直变大 C．地面对斜面体的摩擦力一直变小 D．斜面体对小球的支持力一直变大 【解答】解：AD、根据题意，作出小球受力的矢量三角形，如图所示 沿逆时针方向缓慢转动弹簧秤，从图中可看出力F先减小再增大，斜面对球得支持力一直减小，故AD错误； BC、对斜面和小球整体受力分析，由平衡条件得： 竖直方向：N＝（mg+G）﹣F y 水平方向：f＝F x 现沿逆时针方向缓慢转动弹簧秤，所以F 一直增大，F 一直减小，因此N一直减小，f一直减小，故D错误， y x C正确。 故选：C。第 6 讲 牛顿第一定律 牛顿第三定律 1.理解牛顿第一定律的内容和惯性，会分析实际问题. 2.理解牛顿第三定律的内容，会区分相互作用力和平衡力． 考点一 牛顿第一定律的理解与应用 1．内容 一切物体总保持匀速直线运动状态或静止状态，除非作用在它上面的力迫使它改变这种状态． 2．意义 (1)指出力不是维持物体运动的原因，而是改变物体运动状态的原因，即力是产生加速度的原因． (2)指出了一切物体都有惯性，因此牛顿第一定律又称为惯性定律． (3)牛顿第一定律描述的只是一种理想状态，而实际中不受力作用的物体是不存在的，当物体受外力但所受合力为 零时，其运动效果跟不受外力作用时相同，物体将保持静止或匀速直线运动状态． 3．惯性 (1)定义：物体具有保持原来匀速直线运动状态或静止状态的性质． (2)量度：质量是物体惯性大小的唯一量度，质量大的物体惯性大，质量小的物体惯性小． (3)普遍性：惯性是物体的固有属性，一切物体都有惯性，与物体的运动情况和受力情况无关．[例题1] （2024•福州模拟）闽江河口龙舟竞渡历史可追溯到秦汉，那时河口居有一支闽越王无诸氏族， 他们擅长划舟，喜赛龙舟，留下了龙舟竞渡传统。《福州地方志》记载：“福州龙舟竞渡，台江、西湖皆有 之。”图为龙舟比赛的照片，下列说法正确的是（ ） A．龙舟的速度越大，惯性也越大 B．获得冠军的龙舟，其平均速度一定最大 C．龙舟齐头并进时，相对于河岸是静止的 D．龙舟能前进是因为水对船桨的作用力大于船桨对水的作用力 【解答】解：A、质量是惯性大小的唯一量度，与速度的大小无关，故A错误； B、在比赛时是相同距离下比较时间，即比较平均速度的大小，平均速度大，时间短，获得冠军，故B正确； C、龙舟齐头并进时，相对于河岸是运动的，故C错误； D、水对船桨的作用力与船桨对水的作用力是一对相互作用力，大小相等，方向相反，故D错误； 故选：B。 [例题2] （2024•兰州模拟）在东汉王充所著的《论衡•状留篇》中提到“是故湍濑之流，沙石转而大石 不移。何者？大石重而沙石轻也。”从物理学的角度对文中所描述现象的解释，下列说法正确的是（ ） A．水冲沙石，沙石才能运动，因为力是产生运动的原因 B．“沙石转而大石不移”是因为物体运动状态改变的难易程度与质量有关 C．只有在水的持续冲力作用下沙石才能一直运动，是因为运动需要力来维持 D．“大石不移”是因为大石受到的阻力大于水的冲力 【解答】解：A、水冲沙石，沙石才能运动，因为水的冲击力克服了阻力，故力是改变运动状态的原因，故A 错误； B、物体总有保持原有运动状态的性质即为惯性，其大小只与质量有关，质量越大惯性越大，力是改变物体运 动状态的原因，重的大石由于质量太大，惯性太大，所以运动状态不容易被水流改变，故B正确； C、物体的运动不需要力来维持，如沙石不受力的作用时，可以做匀速直线运动状态，故C错误； D、“大石不移”是因为水的冲力等于大石受到的阻力，大石所受的合外力为零，故D错误。 故选：B。 [例题3] （2023•海口模拟）下列有关力和运动，说法正确的是（ ） A．把手中的铅球静止释放，铅球竖直下落是因为惯性B．汽车的速度越大，刹车时越难停下来，说明速度越大惯性越大 C．牛顿第一定律也被叫作惯性定律 D．汽车紧急刹车时乘客向前倾，是因为乘客受到向前的惯性力 【解答】解：A．把手中的铅球由静止释放后，球能竖直下落，是由于球受到竖直向下的重力的缘故，故A错 误； B．惯性是物体总保持匀速直线运动状态或静止状态的性质，是物体的固有属性，惯性的大小只与物体的质量 有关，质量越大，物体的惯性越大，故惯性与速度无关，故B错误； C．牛顿第一定律指出：一切物体总保持匀速直线运动状态或静止状态，除非作用在它上面的力迫使它改变这 种状态，也叫“惯性定律”，故C正确； D．汽车紧急刹车时，乘客会向前倾倒，这是由于乘客具有惯性；惯性不是力，不能说受到惯性力的作用，故 D错误。 故选：C。 考点二 牛顿第三定律的理解与应用 1．牛顿第三定律的内容 两个物体之间的作用力和反作用力总是大小相等、方向相反、作用在同一条直线上． 2．作用力与反作用力的“三同、三异、三无关” (1)“三同”：①大小相同；②性质相同；③变化情况相同． (2)“三异”：①方向不同；②受力物体不同；③产生的效果不同． (3)“三无关”：①与物体的种类无关；②与物体的运动状态无关；③与物体是否和其他物体存在相互作用无关． 3．相互作用力与平衡力的比较 对应名称 作用力和反作用力 一对平衡力 比较内容 作用在两个相互作用的物体上 作用在同一物体上 同时产生、同时消失 不一定同时产生、同时消失 两力作用效果不可抵消，不可叠加，不可 两力作用效果可相互抵消，可叠加，可 不同点 求合力 求合力，合力为零 一定是同性质的力 性质不一定相同 大小相等、方向相反、作用在同一条直 相同点 线上 [例题4] （2024•惠州一模）如图所示，一女士借助瑜伽球靠墙静止蹲在墙边，女士背部保持挺直且倚靠在瑜伽球上，瑜伽球“倚靠”在竖直墙面上。下列说法正确的是（ ） A．地面对女士的支持力大于女士受到的重力 B．地面对女士的摩擦力为零 C．女士对瑜伽球的弹力可能为0 D．女士对瑜伽球的弹力与墙壁对瑜伽球的弹力是一对相互作用力 【解答】解：A、瑜伽球有向下的运动趋势，墙壁和女士对球有竖直向上的摩擦力。女士受到竖直向下的重力、 瑜伽球对女士向下的摩擦力和地面竖直向上的支持力，根据平衡条件可知地面对女士的支持力等于重力与摩擦 力之和，所以地面对女士的支持力大于女士受到的重力，故A正确； B、女士在水平方向上受力平衡，由于瑜伽球对女士有水平向左的弹力，所以地面对女士有水平向右的摩擦力， 故B错误； C、瑜伽球在水平方向受力平衡，墙壁对瑜伽球有水平向左的弹力，所以女士对瑜伽球有水平向右的弹力，故C 错误； D、女士对瑜伽球的弹力与墙壁对瑜伽球的弹力都作用在瑜伽球上，是一对平衡力，故D错误。 故选：A。 [例题5] （2024•浙江模拟）2023年10月7日，第19届亚运会皮划艇静水项目中浙江选手李冬盎以 1分 58秒931的成绩获得皮划艇静水女子500米单人皮艇决赛冠军，如图为运动员冲刺时的照片。下列说法一定 正确的是（ ） A．研究冲刺瞬间的划水动作时可以将运动员视为质点 B．“1分58秒931”是指时间间隔 C．桨对水的作用力大于水对浆的作用力 D．运动员冲刺的瞬时速度约为4.2m/s 【解答】解：A、在冲刺瞬间，船的长度不能忽略不急，此时不能将船视为质点，故A错误； B、“1分58秒931”是指比赛时间，故B正确； C、桨对水的作用力与水对桨的作用力是一对相互作用力，大小相等，故C错误；D、根据题意无法得出比赛冲刺时的瞬时速度，故D错误； 故选：B。 [例题6] （2024•南充模拟）如图，木模A、B质量均为m，通过三根轻质竖直细线对称连接，木模B静 止在水平面上。细线a、b、c上的拉力大小分别用F 、F 、F 表示，水平面所受的压力大小为F ，重力加速 a b c N 度大小为g。下列说法正确的是（ ） A．F ＝F +F +mg B．F ＜2mg a b c N C．F +F +F ＝2mg D．F ＝F +F a b c a b c 【解答】解：AD．研究对象为木模A，对木模A受力分析有：F ＝F +F +mg，故A正确，D错误； a b c B．求水平面受到的压力，研究对象是整体，故对木模A、B整体有：F′ ＝mg+mg＝2mg N 根据牛顿第三定律可知水平面所受的压力大小为：F ＝F′ ＝2mg，故B错误； N N C．由：F +F +F ＝2F +2F +mg≠2mg，故C错误。 a b c b c 故选：A。 考点三 “转移研究对象法”在受力分析中的应用 作用力与反作用力，二者一定等大反向，分别作用在两个物体上．当待求的某个力不容易求时，可先求它的反作 用力，再反过来求待求力．如求压力时，可先求支持力．在许多问题中，摩擦力的求解亦是如此． [例题7] （2023•广州三模）如图所示，小明同学在家做家务时，沿轻质推杆方向斜向下施加力，拖把受 到杆的推力F与水平方向的夹角为θ，且拖把刚好做匀速直线运动，则（ ） A．拖把所受地面的摩擦力为Fsinθ B．地面对拖把的支持力大于拖把的重力C．推杆对拖把的作用力大于拖把对推杆的作用力 D．推杆对拖把的作用力小于拖把对推杆的作用力 【解答】解：AB、拖把的受力图如下 根据正交分解可得 Fcosθ＝F f F ＝mg+Fsinθ N 所以，拖把所受地面的摩擦力为Fcosθ；地面对拖把的支持力大于拖把的重力，故A错误，B正确； CD、根据牛顿第三定律，可知推杆对拖把的作用力与拖把对推杆的作用力是相互作用力，等大反向，故 CD错 误。 故选：B。 [例题8] （2022•昌平区二模）激光是20世纪60年代发明的一种新型光源，它有很多特点，其中之一是 光束截面上光强分布不均匀，中心强，向外依次减弱，也可以这样理解：如图甲中的一束激光，经焦点 F会 聚后向下照射，光线①由单个光子hv构成，光线②由双光子2hv构成，光线③由三光子3hv构成，能量最大。 如图乙所示，一透明微粒处于向下照射的激光束中，微粒中心 O位于激光束中心轴MN左侧，激光束穿过微 粒时发生了折射（图中只画出两条光线，且强度②＞①），微粒的折射率大于周围介质的折射率，不考虑光 的反射和吸收。入射光束由光子组成，光子在与微粒作用时速度方向发生了改变，说明微粒对光子施加了作 用力。下列说法正确的是（ ） A．光线①对微粒的作用力方向为向右偏上 B．光线②对微粒的作用力方向为向左偏上 C．光线①和光线②对微粒的作用力大小相等D．光线①和光线②对微粒作用力的合力会将微粒推向光束中心 【解答】解：A．光线①对微粒的作用力方向为向左偏下，故A错误； B．光线②对微粒的作用力方向为向右偏下，故B错误； C．光线①和光线②的能量不等，则对微粒的作用力大小不等，故C错误； D．虽然图中只画出两条光线，但实际上光束中心左侧的光线会多于光束中心右侧的光线，光线①和光线②对 微粒作用力的合力会将微粒推向光束中心，故D正确。 故选：D。 [例题9] （2023•邵阳三模）在楼房维修时，为防止重物碰撞阳台，工人经常使用如图所示的装置提升重 物。跨过光滑定滑轮的a绳和b、c绳子连结在O点，工人甲拉动绳的一端使重物上升，工人乙在地面某固定 位置用力拉着b绳的一端，保证重物沿竖直方向匀速上升，则下列说法正确的是（ ） A．a绳的拉力先变大后变小 B．b绳的拉力越来越小 C．工人乙对地面的压力越来越大 D．工人乙对地面的摩擦力越来越大 【解答】解：AB、重物沿竖直方向匀速上升，O点受到c绳的拉力大小等于重物的重力，受力分析如图所示 当物体上升时，a绳与竖直方向的夹角变大，b绳与竖直方向的夹角变小，根据平行四边形法则可知 ab绳中的 拉力都变大，故AB错误； C、工人乙在竖直方向受到b段绳子拉力的竖直分力越来越大，根据平衡条件可知，地面对乙的支持力越来越 小，由牛顿第三定律可知，工人乙对地面的压力越来越小，故C错误； D、由于a段绳子拉力越来越大，与竖直方向的夹角越来越大，其水平方向的分力越来越大，对重物和乙整体分析，水平方向根据平衡条件可知，工人乙受到地面的摩擦力等于a段绳子水平方向的分力，故工人乙受到地 面的摩擦力越来越大，由牛顿第三定律知，工人乙对地面的摩擦力越来越大，故D正确。 故选：D。 题型1对牛顿第一定律的理解 1. （2022•银川模拟）根据牛顿第一定律，以下说法不正确的是（ ） A．牛顿第一定律说明力是改变物体运动状态的原因 B．在宇宙飞船内物体不存在惯性 C．物体运动状态发生了改变，必定受到外力的作用 D．歼击机在进入战斗状态时要丢掉副油箱，这样做是为了减小惯性 【解答】解：A、由牛顿第一定律可知，当物体不受力或受平衡力时，物体将处于静止状态或匀速直线运动状 态，因此力是改变物体运动状态的原因，故A正确； B、惯性是物体的固有属性，物体在任何状态下均有惯性，则在宇宙飞船内物体有惯性，故B不正确； C、力是改变物体运动状态的原因，体运动状态发生了改变，必定受到外力的作用；故C正确； D、惯性只与质量有关，质量越小，惯性越小，越容易改变运动状态，则歼击机在进入战斗状态时要丢掉副油 箱，这样做是为了减小惯性，有利于运动状态的改变；故D正确； 本题选择不正确的，故选：B 2. （2023•梅州一模）早在2300年前，墨子在《墨经》中就对力的概念提出了初步的论述：“力，形之 所以奋也。”这句话的意思是说，力是使物体开始运动或加快运动的原因。则下列关于力的说法正确的是（ ） A．墨子的观点与亚里士多德关于力和运动的观点基本相同 B．物体受到变力作用，速度大小一定会改变 C．力不是维持物体运动的原因 D．当物体不受力时，物体将停止运动 【解答】解：A、墨子的观点与伽利略关于力和运动的观点基本相同，故A错误； B、物体受到变力作用，物体的运动状态一定发生改变，即物体的速度一定发生变化，但是速度的大小不一定 会改变，例如物体做匀速圆周运动，故B错误。 C、力不是维持物体运动的原因，而是改变物体运动状态的原因，故C正确。 D、当物体不受力时，物体的运动状态不发生变化，即物体保持静止或匀速直线运动状态不变，运动的物体不会停止运动，故D错误。 故选：C。 题型2惯性与质量 3. （2023•广东模拟）机器人服务人类的场景正步入现实生活中，例如餐厅中使用机器人来送餐，就越 来越常见。如图甲所示为某餐厅的送餐机器人，将其结构简化为如图乙所示的示意图，机器人的上表面保持 水平。则下列说法中正确的是（ ） A．菜品随着机器人一起做匀速直线运动时，菜品受到与运动方向一致的摩擦力作用 B．菜品随着机器人一起做匀速直线运动时，菜品对机器人的压力和机器人对菜品的支持力是一对平衡力 C．菜品随着机器人一起做匀加速直线运动时，菜品的惯性逐渐增大 D．菜品随着机器人一起做匀减速直线运动时，机器人对菜品的作用力大于菜品的重力 【解答】解：A、菜品随着机器人一起做匀速直线运动时，菜品所受合力为零，故菜品不受摩擦力的作用；故 A错误； B、菜品对机器人的压力和机器人对菜品的支持力分别作用在两个不同的物体上，是作用力和反作用力关系。 不是一对平衡力，故B错误； C、惯性是物体的固有属性，与物体的运动状态无关，故C错误； D、菜品随着机器人一起做匀减速直线运动时，机器人对菜品的作用力在竖直方向的分力等于菜品的重力，机 器人对菜品还有沿水平方向的分力，所以机器人对菜品的作用力大于菜品的重力，故D正确； 故选：D。 4. （2023•丽江一模）如图所示，在一辆表面光滑的小车上，放有质量分别为m 、m 的两个球，随车 1 2 一起匀速运动，当车突然停止运动，其他阻力不计，设车无限长，则两小球（ ） A．一定相碰 B．一定不相碰C．若m ＞m ，则肯定相碰 1 2 D．若m ＜m ，则一定不相碰 1 2 【解答】解：车停止前，两个小球和小车一起做匀速直线运动，并且两个小球和小车具有共同的速度，当小车 突然停止时，由于小球在光滑接触面上，因此两个小球由于惯性，还要保持原来大小不变的速度做匀速直线运 动，由于两球的速度相同，相等时间内通过的位移相等，因此两个小球间的距离不变，一定不会相碰。 故选：B。 题型3牛顿第三定律应用 5. （2023•绍兴二模）如图所示，拖车的缆绳将违章车与拖车拴在一起，使违章车停在倾斜坡道上保持 静止状态。下列说法正确的是（ ） A．缆绳对违章车的拉力等于违章车对缆绳的拉力 B．违章车对坡道的作用力的方向一定与坡道垂直 C．坡道与水平面的夹角越小，坡道受到的压力也越小 D．违章车一定只受到重力、支持力、拉力三个力的作用 【解答】解：A．根据牛顿第三定律可知，缆绳对违章车的拉力等于违章车对缆绳的拉力，故A正确； B．违章车受到重力，支持力和绳子的拉力，当拉力等于重力沿斜坡的分力时，违章车对坡道没有摩擦力作用， 若拉力小于重力分力，那么斜坡对轨道有摩擦，因此违章车对斜坡的作用力可能是摩擦力和支持力的合力，这 个合力与坡道不垂直；若违章车只受坡道的支持力，没有摩擦力，违章车对坡道的作用力的方向与坡道垂直， 故B错误； C．设坡道与水平面的夹角为θ，则F ＝mgcosθ N 坡道与水平面的夹角越小，坡道受到的压力越大，故C错误； D．违章车除了受到重力、支持力、拉力之外还有可能受到坡道对它的摩擦力，故D错误。 故选：A。 6. （2023•潮州二模）如图所示为智能机器人协助派件员分拣快递的场景，派件员将包裹放在机器人的 水平托盘上后，机器人通过扫码读取目的地信息，并生成最优路线，将不同目的地的包裹送至不同的位置， 从而实现包裹的分拣功能。关于机器人和包裹，下列说法正确的是（ ）A．机器人加速前进则包裹对水平托盘的摩擦力方向向后 B．包裹受到向上的支持力是包裹发生形变产生的 C．包裹对机器人的压力和机器人对包裹的支持力是一对平衡力 D．包裹随着机器人一起做匀速直线运动时，包裹受到向前的摩擦力 【解答】解：A、机器人加速前进时，相对包裹机器人有向前运动的趋势，故此时包裹具有向前的加速度，所 以受到向前的摩擦力作用，根据牛顿第三定律可知包裹对水平托盘的摩擦力方向向后，故A正确； B、包裹受到向上的支持力是托盘发生形变产生的，故B错误； C、包裹对机器人的压力和机器人对包裹的支持力是一对相互作用力，故C错误； D、包裹随着机器人一起做匀速直线运动时，包裹加速度为零，故此时不受到摩擦力，故D错误。 故选：A。 7. （2023•邯山区校级二模）“电动平衡车”是青少年非常喜欢的一种代步工具。如图所示，人站在 “电动平衡车”上在某水平地面上沿直线前进，不计空气阻力，下列说法中正确的是（ ） A．“电动平衡车”加速行驶时，车对人的作用力等于人的重力 B．“电动平衡车”匀速行驶时，车对人的作用力大小等于人对车的压力大小 C．“电动平衡车”加速行驶时，车对人的作用力方向竖直向上 D．“电动平衡车”匀速行驶时，平衡车受到的重力和地面对平衡车的支持力是一对平衡力 【解答】解：A、人受”电动平衡车”的作用力和“电动平衡车”受到人的作用力是一对作用力和反作用力， 二者总是大小相等，方向相反，故A错误； B、“电动平衡车”匀速行驶时人受到的合外力等于零，所以车对人的作用力即人受到的支持力，大小等于人 对车的压力大小，故B正确； C、“电动平衡车”加速行驶时，人受到的合力的方向向前，车对人的作用力方向斜向上，故C错误； D、“电动平衡车”匀速行驶时，平衡车受到的重力与人的重力的和与地面对平衡车的支持力是一对平衡力， 故D错误。 故选：B。题型4作用力和反作用力与一对平衡力的区别 8. （2022•沈北新区校级模拟）如图所示是智能快递分拣机器人，派件员将包裹放在机器人的水平托盘 上后，机器人通过打码读取目的地信息，并生成最优路线，将不同目的地的包裹送至不同的位置．从而实现 包裹的分拣功能。关于机器人下列说法正确的是（ ） A．机器人的轮胎上印有花纹，是为了增大摩擦力 B．包裹受到向上的支持力是包裹发生形变产生的 C．包裹对机器人的压力和机器人对包裹的支持力是一对平衡力 D．包裹随着机器人一起做匀速直线运动时，包裹受到向前的摩擦力 【解答】解：A、机器人的轮胎上印有花纹，是为了增大接触面的粗糙程度，增大摩擦力，故A正确； B、包裏受到向上的支持力是托盘发生形变产生的，故B错误； C、包裹对机器人的压力和机器人对包裹的支持力是一对作用力和反作用力，不是一对平衡力，故C错误； D、包裹随着机器人一起做匀速直线运动时处于平衡状态，包裹不受摩擦力，故D错误。 故选：A。 9. 2021年8月3日，东京奥运会体操女子平衡木单项决赛结束，中国选手管晨辰、唐茜靖包揽金、银 牌。比赛中，体操运动员站在水平的平衡木上处于静态平衡状态，如图所示。则下列说法正确的是（ ） A．平衡木对人的支持力大小等于人对平衡木的压力大小 B．平衡木对人的支持力和人对平衡木的压力是一对平衡力 C．平衡木对人有摩擦力 D．人受到支持力是因为脚底发生了形变 【解答】解：AB、平衡木对人的支持力大小与人对平衡木的压力是一对相互作用力，大小相等，故 A正确，B 错误； C、人站在平衡木上处于静止状态，根据物体的受力平衡分析，人只受重力和平衡木对人的支持力，没有摩擦 力，故C错误； D、人受到支持力是因为平衡木发生了形变，故D错误；故选：A。 10. 疫情复课以后，教室里通常会用磁扣将《通风、消毒记录表》“吸”在竖直黑板上，如图所示．磁 扣与纸始终处于静止状态．下列说法中正确的是（ ） A．记录表受4个力作用 B．磁扣对记录表的摩擦力竖直向上 C．记录表受到黑板的作用力等于记录表的重力 D．磁扣对黑板的吸引力与黑板对磁扣的吸引力是一对相互作用力 【解答】解：A.记录表受重力、磁扣的压力和摩擦力、黑板的支持力和摩擦力5个力的作用，故A错误； B.磁扣受到的摩擦力竖直向上，根据作用力与反作用力的关系可知，对记录表的摩擦力竖直向下，故B错误； C.记录表受到黑板和磁扣的作用力的合力等于记录表的重力，故C错误； D.磁扣对黑板的吸引力的施力物体是磁扣，受力物体是黑板；黑板对磁扣的吸引力的施力物体是黑板，受力物 体是磁扣，故两个力的一对相互作用力，故D正确。 故选：D第 7 讲 牛顿第二定律 两类运动学问题 1.理解牛顿第二定律的内容、表达式及性质. 2.应用牛顿第二定律解决瞬时问题和两类动力学问题． 3.牛顿运动定律在其他模型上的应用 考点一 瞬时加速度的求解 1．牛顿第二定律 (1)表达式为 F ＝ ma . (2)理解：核心是加速度与合外力的瞬时对应关系，二者总是同时产生、同时消失、同时变化． 2．两类模型 (1)刚性绳(或接触面)——不发生明显形变就能产生弹力的物体，剪断(或脱离)后，其弹力立即消失，不需要形变恢 复时间．(2)弹簧(或橡皮绳)——两端同时连接(或附着)有物体的弹簧(或橡皮绳)，特点是形变量大，其形变恢复需要较长时 间，在瞬时性问题中，其弹力的大小往往可以看成保持不变． [例题1] （多选）（2024•南充模拟）如图，矩形框Q用与斜面平行的细绳系在固定的斜面体上，和Q质 量相等的物体P被固定在矩形框中的竖直轻弹簧上端，斜面体倾角为 30°，整个装置保持静止状态，不计矩形 框和斜面间的摩擦，重力加速度为 g，当细绳被剪断的瞬间，物体P的加速度大小a 和矩形框Q的加速度大 P 小a 分别为（ ） Q g A．a ＝0 B．a ＝g C．a = D．a ＝g P P Q 2 Q 【解答】解：AB．对物体P进行受力分析，受到了重力和弹簧的弹力，处于平衡状态，合力为零，细绳被剪断 的瞬间，弹簧弹力不会发生突变，故物体P的受到的合力仍为零，故加速度a ＝0，故A正确，B错误； P CD．对PQ整体分析，受到了重力，斜面的支持力，细线的拉力，整体系统处于静止状态，根据平衡条件有 T＝2mgsinθ 细绳被剪断的瞬间，细线的力就突变成零了，物体Q的受力合外力情况会与之前的拉力T等大反向，即 F合 ＝T＝2mgsinθ 所以 2mgsinθ a = =g Q m 故C错误，D正确。 故选：AD。 [例题2] （2023•蚌埠模拟）如图所示，A、B两物体用两根轻质细线分别悬挂在天花板上，两细线与水 平方向夹角分别为60°和45°，A、B间拴接的轻弹簧恰好处于水平状态，则下列计算正确的是（ ） A．A、B所受弹簧弹力大小之比为√3：√2 B．A、B的质量之比为m ：m =√3：1 A B C．悬挂A、B的细线上拉力大小之比为1：√2D．同时剪断两细线的瞬间，A、B的瞬时加速度大小之比为3：√6 【解答】解：A、对AB受力如图，弹簧处于水平静止状态，弹簧的合力为零，即 A对弹簧的力和B对弹簧的 力大小相等，故A、B受弹簧的弹力大小相等，故A错误； m √3 B、对A受力分析可知m g＝Ftan 60°，对B受力分析可知m g＝F tan45°，联立解得 A = ，故B正确； A B m 1 B F F T √2 C、细线对A的拉力T = ，细线对B的拉力T = ，联立解得 A = ，故C错误； A cos60° B cos45° T 1 B D、剪断细线前，弹簧弹力F＝m g，剪断细线瞬间弹簧弹力不变，A受合力为2m g，故解得A的加速度a B B A 2√3 = g，B的加速度为√2g，故A，B加速度之比为√6：3，故D错误。 3 故选：B。 [例题3] （多选）（2023•鄱阳县校级一模）如图所示，A、B、C三球的质量均为m，轻质弹簧一端固定 在斜面顶端、另一端与A球相连，A、B间由一轻质细线连接，B、C间由一轻杆相连。倾角为θ的光滑斜面 固定在地面上，弹簧、细线与轻杆均平行于斜面，初始系统处于静止状态，细线被烧断的瞬间，下列说法正 确的是（ ） A．A球的加速度沿斜面向上，大小为2gsinθ B．C球的受力情况未变，加速度为0 C．B、C两球的加速度均沿斜面向下，大小均为gsinθ D．B、C之间杆的弹力大小不为0 【解答】解：A、据题意，对A球受力分析，受到重力G 、垂直斜面向上的支持力N 、沿斜面向上的弹力F A A 和B、C球对它的拉力T ，由于A球处于静止状态， A 则据平衡条件有：F＝G A sinθ+T A ＝3mgsinθ ① 现将细线烧断，据弹簧弹力具有瞬间保持原值的特性， 则有：F﹣G sinθ＝ma，② A由①、②可得A球此时加速度：a＝2gsinθ， 故A正确； B、细线烧断后，把B、C球看成一个整体，它们只受到重力和支持力，它们以相同的加速度 a＝gsinθ沿斜面向 下，所以B、C之间杆的弹力大小为零，故B、D选项错误，而C选项正确。 故选：AC。 考点二 动力学中的图象问题 1．动力学中常见的图象v－t图象、 x － t 图象、F－t图象、F－a图象等． 2．解决图象问题的关键：(1)看清图象的横、纵坐标所表示的物理量及单位并注意坐标原点是否从零开始。 (2)理解图象的物理意义，能够抓住图象的一些关键点，如斜率、截距、面积、交点、拐点等，判断物体的运动情 况或受力情况，再结合牛顿运动定律求解． [例题4] （2024•平谷区模拟）用水平拉力使质量分别为m甲 、m乙 的甲、乙两物体在水平桌面上由静止开 始沿直线运动，两物体与桌面之间的动摩擦因数分别为 μ甲 和μ乙 。甲、乙两物体运动后，所受拉力F与其加 速度a的关系图线如图所示，由图可知（ ） A．m甲 ＞m乙 ，μ甲 ＞μ乙 B．m甲 ＞m乙 ，μ甲 ＜μ乙 C．m甲 ＜m乙 ，μ甲 ＞μ乙 D．m甲 ＜m乙 ，μ甲 ＜μ乙 【解答】解：物体在水平桌面上运动，在拉力F和滑动摩擦力的作用下做加速运动，根据牛顿第二定律有 F﹣μmg＝ma，可知F﹣a图像的斜率表示物体的质量，则有m甲 ＞m乙 ，纵截距表示物体所受的滑动摩擦力大小， 则甲、乙受到的滑动摩擦力大小相等，又m甲 ＞m乙 ，则有μ甲 ＜μ乙 ， 故B正确，ACD错误。 故选：B。 [例题5] （多选）（2023•河西区三模）用一水平力F拉静止在水平面上的物体，在外力F从零开始逐渐 增大的过程中，物体的加速度a随外力F变化的关系如图所示，g＝10m/s2。则下列说法正确的是（ ）A．物体与水平面间的最大静摩擦力为14N B．物体做变加速运动，F为14N时，物体的加速度大小为7m/s2 C．物体与水平面间的动摩擦因数为0.3 D．物体的质量为2kg 【解答】解：A.由题图可知，物体与水平面间的最大静摩擦力为f ＝7N，故A错误； m B.由于外力F不断变化，根据牛顿第二定律F﹣f＝ma，可知物体加速度不断变化，做变加速运动；当F ＝14N 2 时，由a﹣F图像可知a =4m/s2，故B错误； 2 CD.当F ＝7N时，根据牛顿第二定律F ﹣μmg＝ma ，当F ＝14N时，根据牛顿第二定律F ﹣μmg＝ma ，代入 1 1 1 2 2 1 上式解得m＝2kg，μ＝0.3，故CD正确，B错误。 故选：CD。 [例题6] 艾萨克•牛顿在《自然哲学的数学原理》一书中指出：“力使物体获得加速度。”某同学为探究 加速度与力的关系，取两个材质不同的物体A、B，使其分别在水平拉力F的作用下由静止开始沿水平面运动， 测得两物体的加速度 a与拉力F之间的关系如图所示，重力加速度 g取10m/s2，空气阻力忽略不计，则 （ ） A．物体A的质量为0.7kg B．物体B的质量为0.2kg C．物体A与水平面间动摩擦因数为0.5 D．物体B与水平面间动摩擦因数为0.1 【解答】解：AC.对物体A由牛顿第二定律F ﹣μ m g＝m a A A A A A 由图像可知7N＝μ m g A A −μ m g=m ×(−5m/s2 ) A A A 联立解得：m ＝1.4kg，μ ＝0.5 A A故A错误，C正确； BD.对B同理可知2N＝μ m g B B −μ m g=m ×(−2m/s2 ) B B B 联立解得：μ ＝0.2，m ＝1kg B B 故BD错误。 故选：C。 考点三 连接体问题 1．整体法的选取原则 若连接体内各物体具有相同的加速度，且不需要求物体之间的作用力，可以把它们看成一个整体，分析整体受到 的合外力，应用牛顿第二定律求出加速度(或其他未知量)． 2．隔离法的选取原则 若连接体内各物体的加速度不相同，或者要求出系统内各物体之间的作用力时，就需要把物体从系统中隔离出来， 应用牛顿第二定律列方程求解． 3．整体法、隔离法的交替运用 若连接体内各物体具有相同的加速度，且要求出物体之间的作用力时，可以先用整体法求出加速度，然后再用隔 离法选取合适的研究对象，应用牛顿第二定律求作用力．即“先整体求加速度，后隔离求内力”． [例题7] （2023•盐山县二模）如图所示，质量分别为1kg和2kg的A、B两个物体放在光滑水平面上， 外力F 、F 同时作用在两个物体上，其中 F ＝10﹣t（表达式中各个物理量的单位均为国际单位），F ＝ 1 2 1 2 10N。下列说法中正确的是（ ） A．t＝0时，物体A的加速度大小为10m/s2 B．t＝10s后物体B的加速度最小 C．t＝10s后两个物体运动方向相反 D．若仅将A、B位置互换，t＝0时物体A的加速度为8m/s2 【解答】解：A．F 在水平方向上的分力为 2 F ＝F cos37°＝10×0.8N＝8N 21 2 F 8 假设A、B间无弹力，则a = 21= m/s2＝4m/s2 B m 2 Bt＝0时，有F ＝10N 1 假设A、B间无弹力，则 F 10 a = 1 = m/s2＝10m/s2＞a A m 1 B A 因此t＝0时，A会推动B一起运动，对AB整体，由牛顿第二定律有F +F ＝（m +m ）a 1 21 A B 代入数据解得a＝6m/s2 故A错误； F 10−t B．物体B的加速度最小时，A、B间没有力的作用，且a ＝a a = 1 = A B A m 1 A F 8 a = 21= m/s2＝4m/s2 B m 2 B 解得t＝6s 故B错误； C．t＝10s前，A、B均沿F 方向加速运动；t＝10s后，F 方向反向，A做减速运动，但两物体运动方向仍然相 1 1 同，故C错误； D．若仅将A、B位置互换，t＝0时，假设A、B间无弹力，则 F 8 a = 21= m/s2＝8m/s2 A1 m 1 A F 10 a = 1 = m/s2＝5m/s2＜a B1 m 2 A1 B 表明A、B会分离运动，故假设正确，则t＝0时物体A的加速度为8m/s2，故D正确。 故选：D。 [例题8] （2023•河南模拟）如图1所示，物体A、B放在粗糙水平面上，A、B与地面间的动摩擦因数均 为μ＝0.1，m ＝2kg，m ＝1kg，A、B分别受到的随时间变化的力F 与F ，如图2所示。已知重力加速度g A B A B ＝10m/s2，下列说法正确的是（ ） A．两物体在t＝1s时分离B．两物体分离时的速度为5m/s C．两物体分离时的速度为4.875m/s D．两物体一起做加速运动 【解答】解：由图2知F 与t的关系式为：F ＝12﹣2t，F 与t的关系式为：F ＝3t，A的摩擦力为f ＝μm g＝ A A B B A A 0.1×2×10N＝2N，B的摩擦力为f ＝μm g＝0.1×1×10N＝1N。 B B A、物体A、B分离时，A、B加速度相等，速度相同，但A、B间无弹力，则对A、B受力分析，由牛顿第二 定律可知， 12−2t−2 3t−1 分离时A物体：F ﹣f ＝m a ，B物体：F ﹣f ＝m a ，当a ＝a ，即 m/s2= m/s2 ，解得t A A A A B B B B A B 2 1 ＝1.5s，故A错误； BC、对AB整体分析从开始到分离过程由动量定理，取向右为正，I +I −f t−f t=(m +m )v−0，由图 F F A B A B A B 2只图线围成的面积表示冲量可知在1s内， 1 63 1 9 27 A物体F 的冲量I = ×(9+12)×1.5N•s= N•s，B物体F 的冲量I = × ×1.5N•s= N•s，代入数据解 A A 2 4 B B 2 2 8 得：v＝4.875m/s。故B错误，C正确； D、AB分离前一起加速，1.5s后不再一起加速运动，故D错误。 故选：C。 [例题9] （2022•汤原县校级模拟）质量为m的光滑圆柱体A放在质量也为m的光滑“V型槽B上，如图， α＝60°，另有质量为M的物体C通过跨过定滑轮的不可伸长的细绳与B相连，现将C自由释放，则下列说法 正确的是（ ） A．若A相对B未发生滑动，则A、B、C三者加速度相同 B．当M＝2m时，A和B共同运动的加速度大小为g 3(√3+1) C．当M= m时，A与B之间的正压力等于0 2 D．当M=(√3+1)m时，A相对B刚好发生滑动 【解答】解：A、若A相对B未发生滑动，则A、B、C三者加速度大小相同，方向不同，故A错误； 1 B、以整体为研究对象，根据牛顿第二定律可得：Mg＝（M+2m）a，解得：a= g，故B错误； 4 CD、当A和B右端挡板之间的作用力为零时，加速度为 a ，以A为研究对象，根据牛顿第二定律可得： 0√3 mgtan30°＝ma ，解得a = g； 0 0 3 以整体为研究对象，根据牛顿第二定律可得Mg＝（M+2m）a ，解得：M=(√3+1)m，所以A相对B刚好发 0 生滑动时，M=(√3+1)m，故C错误、D正确。 故选：D。 考点四 动力学两类基本问题 求解两类问题的思路，可用下面的框图来表示： 分析解决这两类问题的关键：应抓住受力情况和运动情况之间联系的桥梁——加速度． [例题10]（多选）（2023•海南一模）一种能垂直起降的小型遥控无人机如图所示，螺旋桨工作时能产生 恒定的升力。在一次试飞中，无人机在地面上由静止开始以 2m/s2的加速度匀加速竖直向上起飞，上升36m 时无人机突然出现故障而失去升力。已知无人机的质量为5kg，运动过程中所受空气阻力大小恒为10N，取重 力加速度大小g＝10m/s2。下列说法正确的是（ ） A．无人机失去升力时的速度大小为12m/s B．螺旋桨工作时产生的升力大小为60N C．无人机向上减速时的加速度大小为12m/s2 D．无人机上升的最大高度为36m 【解答】解：A、无人机向上加速过程中，由位移—速度公式得：v2−v2=2ax 0 代入数据解得，无人机失去升力时的速度大小为v＝12m/s 故A正确； B、无人机向上加速过程中，对无人机，由牛顿第二定律得：F﹣mg﹣f＝ma 1代入数据解得：F＝70N 故B错误； C、无人机向上减速时，对无人机，由牛顿第二定律得：mg+f＝ma 2 代入数据解得：a ＝12m/s2 2 故C正确； D、无人机向上减速过程，由位移—速度公式得：v2−v2=2ax 0 代入数据解得，无人机减速上升的高度为x ＝6m 2 则无人机上升的最大高度为H＝x +x ＝36m+6m＝42m 1 2 故D错误。 故选：AC。 [例题11] （2023•分宜县校级一模）如图，长L＝4m的一段平直轨道BC与倾角θ＝37°的足够长光滑斜面 CD相连，一物块（可视为质点）质量m＝2kg，在与水平方向成θ＝37°、斜向左上方的恒力F＝10N作用下， 从静止开始做匀加速直线运动。物块与水平轨道 BC的动摩擦因数为 μ＝0.5（取重力加速度 g＝10m/s2， sin37°＝0.6，cos37°＝0.8，设物块在C点的速度大小保持不变）求： （1）物块运动到C点时的速度大小； （2）物块沿斜面上升的最大高度。 【解答】解：（1）物块从B点运动到C点，对物块受力分析，如图1： 竖直方向：N+Fsin37°＝mg 水平方向：Fcos37°﹣f＝ma 1 又f＝μN 代入数据联立解得：a ＝0.5m/s2 1 由位移—速度公式得：v2 =2a L C 1代入数据解得，物块运动到C点时的速度大小v ＝2m/s C （2）物块沿斜面上升过程，对物块受力分析，如图2： 由牛顿第二定律得F﹣mgsin37°＝ma 2 代入数据解得：a ＝﹣1m/s2 2 由位移—速度公式得：0−v2 =2a x C 2 代入数据解得，物块上滑的最大距离为x＝2m 最大高度h＝xsin37°＝2×0.6m＝1.2m 答：（1）物块运动到C点时的速度大小为2m/s； （2）物块沿斜面上升的最大高度为1.2m。 [例题12]（2024•南宁一模）某种海鸟可以像标枪一样一头扎入水中捕鱼，假设其在空中的俯冲看作自由 落体运动，进入水中后可以看作匀减速直线运动，其v﹣t图像如图所示，自由落体运动的时间为t ，整个过 1 5 程的运动时间为 t ，最大速度为v ＝6m/s，重力加速度g取10m/s2，下列说法正确的是（ ） 3 1 m A．t ＝1s 1 B．整个过程中，鸟下落的高度为3m 5 C．t 至 t 时间内，鸟的加速度大小为20m/s2 1 3 1 5 D．t 至 t 时间内，鸟所受的阻力是重力的1.5倍 1 3 1 【解答】解：A、小鸟自由落体运动的最大速度为v ＝6m/s，由自由落体运动的规律有v ＝gt ，解得t ＝ m m 1 1 0.6s，故A错误； v 5 6 5 B、整个过程下落的高度为图 v﹣t图像与时间轴所围成的面积，则h= m× t = × ×0.6m＝3m，故B正确 2 3 1 2 30−v −6 5 = m = C、t ∽ t 时间内小鸟的加速度a 5 0.4m/s2＝﹣15m/s2，所以加速度大小为15m/s2，故C错误； 1 3 1 t −t 3 1 1 5 f D、t ∽ t 时间内，由牛顿第二定律有f﹣mg＝ma，可得f＝2.5mg，则 =2.5，即阻力是重力的2.5倍，故D 1 3 1 mg 错误。 故选：B。 [例题13]（2023•衡水二模）2022年北京冬季奥运会冰壶比赛的水平场地如图所示，运动员推动冰壶从发 球区松手后，冰壶沿中线做匀减速直线运动，最终恰好停在了营垒中心．若在冰壶中心到达前掷线时开始计 时，则冰壶在第2s末的速度大小v ＝3.2m/s，在第15s内运动了x ＝0.08m，取重力加速度大小g＝10m/s2。 2 15 求： （1）冰壶与冰面间的动摩擦因数μ； （2）营垒中心到前掷线的距离L 。 0 【解答】解：（1）假设冰壶速度减到0后冰壶可以反向退回，则冰壶的加速度大小 Δv 3.2−0.08 156 a= = m/s2= m/s Δt 14.5−2 625 156 若冰壶以加速度= m/s2减速，则冰壶在最后1s通过的位移 625 1 1 156 78 s= at2= × ×12m= m＞x 2 2 625 625 15 所以冰壶在第15s内的某瞬间已经停止运动，令Δt＝1s，设冰壶运动x 所用的时间为t，则有 15 1 x = at2 15 2 v ＝a（12Δt+t） 2 μmg a= =μg m 代入数据解得μ＝0.025 1 （2）根据运动学公式有L = a(14Δt+t) 2 0 2 代入数据解得L ＝27.38m 0 答：（1）冰壶与冰面间的动摩擦因数μ为0.025； （2）营垒中心到前掷线的距离L 为27.38m。 0题型1已知受力情况求运动情况 1. （2023秋•潍坊期末）如图所示，在倾角37°足够长的斜面上有一个质量为1kg的物体，物体与斜面 之间的动摩擦因数为0.5，t＝0时物体在F＝15N拉力的作用下由静止开始沿斜面向上运动，t＝2s时撤去拉力 F。g取10m/s2，sin37°＝0.6。下列说法正确的是（ ） A．物体沿斜面向上加速时加速度大小为2m/s2 B．物体在t＝2.5s时的速度为0 C．物体在斜面上运动的总时间为3s D．物体沿斜面向上运动的最大位移为15m 【解答】解：A.有拉力作用时，对物体受力分析，根据牛顿第二定律可得F﹣mgsinθ﹣μmgcosθ＝ma 1 解得，物体沿斜面向上加速时加速度大小为a ＝5m/s2，故A错误； 1 B.2s时物体的速度为v ＝a t ＝5×2m/s＝10m/s 1 11 撤去拉力后，物体向上滑动的过程中，对物体受力分析，根据牛顿第二定律可得 mgsinθ+μmgcosθ＝ma 2 解得，物体向上减速的加速度大小为a ＝10m/s2 2 v = 则物体向上减速的时间为t ，解得t ＝1s 2 a 2 1 则物体在t＝3s时的速度为0，故B错误； C.当物体速度减为零时，由于mgsinθ＞μmgcosθ则物体不能保持静止，物体会沿斜面向下做加速运动，则物体 在斜面上的运动时间不止3s，故C错误； v v D.物体沿斜面向上运动的最大位移为x= 1 t + 1 t ，解得x＝15m，故D正确。 1 2 2 2 故选：D。 2. 如图，在与水平方向成θ＝37°角斜向上，大小始终不变的拉力F＝6N作用下，质量为m＝1.1kg的物 体（可视为质点）由静止开始从A点在水平面上做匀加速直线运动。到达B点（B点处轨道平滑连接）时撤去拉力F，物体沿倾角为θ＝37°足够长的斜面向上运动，已知l ＝2m，物体与水平面和斜面间的动摩擦因数 AB μ＝0.5。（设最大静摩擦力等于滑动摩擦力，sin37°＝0.6，cos37°＝0.8，重力加速度g取10m/s2，不考虑物体 在B点处速度大小的变化） （1）求物体从A点到B点经过的时间。 （2）请受力分析计算物体上到斜面后能否返回到 B点，如果可以返回B点，计算返回到B点的速度；如果不 能返回B点，计算物体在斜面上移动的最大位移。 【解答】解：（1）对A分析，在水平方向上，根据牛顿第二定律有Fcosθ﹣μ（mg﹣sinθ）＝ma 解得a＝1m/s2 1 根据位移—时间公式有x＝v t+ at2 0 2 解得t＝2s （2）由于mgsinθ＝1.1×10×0.6N＝6.6N＞μmgcosθ＝0.5×1.1×10×0.8N＝4.4N 所以物块可以返回 从A开始运动，第一次到B点的速度为v ＝v +at，解得v ＝2m/s B 0 B 从斜面上减速度的加速度a ，根据牛顿第二定律mgsinθ+μmgcosθ＝ma 2 2 解得a ＝10m/s2 2 根据速度—位移公式v2=v2+2a x B 2 解得x＝0.2m 从斜面下滑的加速度a ，根据牛顿第二定律mgsinθ﹣μmgcosθ＝ma 3 3 解得a ＝2m/s2 3 根据速度—位移公式v'2=v2+2a x B 0 3 2√5 解得v '= m/s B 5 答：（1）物体从A点到B点经过的时间为2s。 2√5 （2）物体可以返回B点，返回到B点的速度为 m/s。 5 L 3. （2023秋•黄埔区校级期末）一质量为5m的羽毛球筒长为L，羽毛球的高度为d= （可将羽毛球看 5成质量集中在球头的质点），如图甲有一质量为m的羽毛球静置于球筒封口顶端（无封口），已知羽毛球和 球筒间的滑动摩擦力恒为f＝2mg，重力加速度为g，不计空气阻力。求：（设球筒一直保持竖直方向运动） （1）如图甲，手握球筒施加竖直向下的恒力F＝2mg使球和球筒由静止开始运动，求球筒落地前羽毛球受到的 摩擦力f ； 0 （2）如图甲，若球筒开口端距地面起始高度为h ，手对球筒施加竖直向下的恒力F＝2mg由静止开始运动，球 1 筒以一定速度撞击桌面后立即静止，而羽毛球球头恰好能碰到桌面（图乙），求h ； 1 （3）如图丙，让球筒开口朝下从离地h 高处由自由下落，球筒撞击地面立即反弹，反弹速率不变。当球筒第 2 一次到达最高点时，羽毛球头刚好滑出球筒，求h 。 2 【解答】解：（1）设球与球筒相对静止，球受摩擦力向下，为f ，加速度为a ，对整体，由牛顿第二定律可得： 0 0 F+（5m+m）g＝（5m+m）a 对羽毛球，则有：mg+f ＝ma 0 0 mg 4 解得 f = ＜f＝2mg，a = g； 0 3 0 3 mg 假设成立，即羽毛球受到的摩擦力大小为 ，方向竖直向下。 3 4 （2）由（1）可知，球筒落地前，球与球筒一起以a = g向下加速，设落地瞬间羽毛球速度为v ，则有v2= 0 3 0 0 2a h 0 1 筒落地后，羽毛球向下减速，设加速度为a ，则有 f﹣mg＝ma 1 1 由题意可知v2=2a （L﹣d） 0 1 3 联立解得h = L； 1 5 （3）落地前，球与筒一起自由落体，设落地瞬间速度为v ，则有v2=2gh 2 2 2接着筒反弹，球仍向下减速，加速度仍为a ＝g（向上）。设筒的加速度为a ，对筒，则有：5mg+f＝5ma ， 1 2 2 7 解得：a = g 2 5 设筒经t到达最高点，则有v ＝a t 2 2 v2 1 由题意得 2 +v t− a t2＝L﹣d 2a 2 2 1 2 49 联立解得h = L。 2 100 题型2已知运动情况求受力情况 4. （2024•顺德区二模）2023年10月31日，神舟十六号载人飞船返回舱在东风着陆场成功着陆。当返 回舱距离地面1.2m时，返回舱的速度为8m/s，此时返回舱底部的4台反推火箭点火工作，使返回舱触地前瞬 间速度降至2m/s，实现软着陆。若该过程飞船始终竖直向下做匀减速运动，返回舱的质量变化和受到的空气 阻力均忽略不计。返回舱的总质量为3×103kg，g取10m/s2，则4台反推火箭点火工作时提供的推力大小为（ ） A．3×104N B．7.5×104N C．2.6×104N D．1.05×105N 【解答】解：根据匀变速直线运动规律有v2−v2=−2aℎ 0 v2−v2 82−22 解得加速度大小为a= 0 = m/s2=25m/s2 2ℎ 2×1.2 返回舱受到重力和反推力，根据牛顿第二定律可得F﹣mg＝ma 解得F＝mg+ma＝3×103×10N+3×103×25N＝1.05×105N 故D正确，ABC错误。 故选：D。 5. （2024•岳阳县校级开学）如图甲所示，鸟儿有多拼，为了生存几只鸟像炮弹或标枪一样一头扎入水 中捕鱼，假设小鸟的俯冲是自由落体运动，进入水中后是匀减速直线运动，其 v﹣t图像如图乙所示，自由落5 体运动的时间为t ，整个过程的运动时间为 t ，最大速度为v ＝18m/s，重力加速度g取10m/s2，下列说法 1 3 1 m 正确的是（ ） A．t ＝1.6s 1 B．整个过程下落的高度为32.4m 5 C．t ～ t 时间内v﹣t图像的斜率为﹣15m/s2 1 3 1 5 D．t ～ t 时间内阻力是重力的1.5倍 1 3 1 【解答】解：A．小鸟自由落体运动的最大速度为v ＝18m/s，由自由落体运动的规律可得v ＝gt ，代入数据 m m 1 解得t ＝1.8s，故A错误； 1 v 5 18 5 B、整个过程下落的高度为图乙v﹣t图像与时间轴所围成的面积，则h= m× t = × ×1.8m＝27m，故B 2 3 1 2 3 错误； −v −18 5 = m = m/s2=−15m/s2 C、t ～ t 时间内小鸟的加速度为a 5 5 ，则此时间内v﹣t图像的斜 1 3 1 t −t ×1.8−1.8 3 1 1 3 率k＝a＝﹣15m/s2，故C正确； 5 f D、t ～ t 时间内由牛顿第二定律有：f﹣mg＝ma，解得： =2.5，故D错误。 1 3 1 mg 故选：C。 6. （2023秋•延庆区期末）如图所示，一位滑雪者与装备的总质量为70kg，以2m/s的初速度沿山坡匀 加速直线滑下，山坡倾角为30°，在4s的时间内滑下的位移为40m。（g取10m/s2）求： （1）滑雪者下滑的加速度a的大小； （2）滑雪者2s末的速度v 的大小； 2 （3）滑雪者受到阻力F 的大小（包括摩擦和空气阻力）。 f1 【解答】解：（1）滑雪者沿山坡向下做匀加速直线运动。根据匀变速直线运动规律，有：x＝v t+ at2 0 2 解得 a＝4m/s2 （2）根据速度—时间公式有v ＝v +at'＝2m/s+4×2m/s＝10m/s 2 0 （3）对滑雪者进行受力分析：滑雪者在下滑过程中，受到重力 mg、山坡的支持力 F 以及阻力F 的共同作用 N f 以滑雪者为研究对象，根据牛顿第二定律有： 沿山坡向下方向有 mgsinθ﹣F＝ma f 解得F＝70N f 答：（1）滑雪者下滑的加速度为4m/s2； （2）滑雪者2s末的速度v 的大小为10m/s； 2 （3）滑雪者受到的阻力是70N。 题型3生活中的超重与失重 7. （2024•嘉兴模拟）如图所示，跳伞运动员打开伞后竖直向下运动。则图示时刻（ ） A．运动员一定处于失重状态 B．伞对运动员的作用力大于运动员对伞的作用力 C．运动员对伞的作用力与空气对伞的作用力可能大小相等 D．空气对运动员和伞的作用力可能大于运动员和伞的总重力 【解答】解：A.图示时刻运动员的加速度无法确定，则运动员不一定处于失重状态，故A错误； B.伞对运动员的作用力和运动员对伞的作用力是一对作用力和反作用力，大小相等，故B错误； C.运动员对伞的作用力与空气对伞的作用力如果大小相等，由于伞的重力不能忽略不计，所以伞和运动员的合力向下，做加速运动，与实际不符，故C错误； D.空气对运动员和伞的作用力可能大于运动员和伞的总重力，伞和运动员的合力向上，做减速运动，与实际相 符，故D正确。 故选：D。 8. （2024•海淀区一模）如图所示，某人站上向右上行的智能电动扶梯，他随扶梯先加速，再匀速运动。 在此过程中人与扶梯保持相对静止，下列说法正确的是（ ） A．扶梯加速运动阶段，人处于超重状态 B．扶梯加速运动阶段，人受到的摩擦力水平向左 C．扶梯匀速运动阶段，人受到重力、支持力和摩擦力 D．扶梯匀速运动阶段，人受到的支持力大于重力 【解答】解：A、人在加速阶段，向右上方加速，根据牛顿第二定律可知，电梯的支持力大于人的重力，所以 人处于超重状态，故A正确； B、加速度运动阶段，根据牛顿第二定律可知，水平方向只有摩擦力提供人的加速度，所以摩擦力方向水平向 右，故B错误； CD、匀速运动阶段，人受力平衡，竖直方向受到重力和支持力且大小相等，水平方向不受力，故CD错误； 故选：A。 9. （2024•天心区校级开学）如图所示，鱼儿摆尾击水跃出水面，吞食荷花花瓣的过程中，下列说法正 确的是（ ） A．鱼儿跃出水面后受力平衡 B．鱼儿跃出水面后处于失重状态 C．鱼儿摆尾击水时，鱼尾击水的力和水对鱼尾的作用力是一对平衡力 D．研究鱼儿摆尾击水跃出水面的动作时可把鱼儿视为质点 【解答】解：AB．鱼儿跃出水面后只受重力作用，加速度向下，受力不平衡，处于失重状态，故 A错误，B正确； C．鱼尾击水的力和水对鱼尾的作用力是两个物体间的相互作用力，一对作用力与反作用力，故C错误； D．物体的形状和大小对于我们所研究的问题可忽略不计时，可把物体看作质点，所以研究鱼儿摆尾击水跃出 水面的动作不可以把鱼儿视为质点，否则就无动作可言，故D错误。 故选：B。 题型4与超重失重有关的图像问题 10. （2024•佛山二模）春节烟花汇演中常伴随无人机表演。如图是两架无人机 a、b同时从同一地点竖直 向上飞行的v﹣t图象。下列说法正确的是（ ） A．t＝5s时，无人机a处于失重状态 B．t＝10s时，无人机a飞到了最高点 C．0～30s内，两架无人机a、b的平均速度相等 D．0～10s内，无人机a的位移小于无人机b的位移 【解答】解：A.0﹣10s无人机a向上做运加速直线运动，根据牛顿第二定律F﹣mg＝ma 1 解得F＝m（g+a ）＞mg 1 无人机处于超重状态，故A错误； B.v﹣t图像的“面积”表示位移，t＝30s时，无人机a飞到了最高点，故B错误； C.v﹣t图像的“面积”表示位移，根据图像可知，两无人机的位移相同，即x ＝x a b x 根据平均速度的定义v= 可知，0～30s内，两架无人机a、b的平均速度相等，故C正确； t D.v﹣t图像的“面积”表示位移，0～10s内，无人机a的位移大于无人机b的位移，故D错误。 故选：C。 11. （2024•河东区二模）图甲是消防员用于观测高楼火灾的马丁飞行背包。在某次演练时，消防员背着 马丁飞行背包从地面开始竖直飞行，其图像如图乙所示，下列说法正确的是（ ）A．消防员上升的最大高度为225m B．消防员在30—90s内处于超重状态 C．消防员在前30s内加速度最大 D．消防员在150—255s内的平均速度大小为零 【解答】解：A.由图像可知，在0～90s内消防员的速度方向均向上，因此在90s时消防员高度达到最大，根据 图像与t轴所围面积即为位移可知，消防员上升的最大高度为h＝675m，故A错误； B.在30～90s内，消防员向上做减速运动，加速度方向向下，因此处于失重状态，故B错误； C.v﹣t图像中，图像斜率为加速度，结合图像可知消防员在前30s内加速度最大，故C正确； D.结合图像可知，消防员在150～255s内，位移大小不为0，因此平均速度不为0，故D错误。 故选：C。 12. （2024•菏泽一模）某同学在手机上放一本《现代汉语词典》并打开手机软件里的压力传感器，托着 手机做下蹲——起立的动作，传感器记录的压力随时间变化的图线如图所示，纵坐标为压力，横坐标为时间。 根据图线下列说法正确的是（ ） A．0～5s内该同学做了2次下蹲——起立的动作 B．起立过程中人始终处于超重状态 C．图中0.5s时人处在下蹲的最低点 D．3s时加速度方向竖直向上 【解答】解：A.下蹲过程包括向下加速、向下减速，对应的状态分别为失重状态和超重状态，起立过程包括向 上加速和向上减速，对应的状态分别为朝中状态和失重状态，结合图像可知，0～5s内该同学做了1次下蹲—— 起立的动作，故A错误；B.起立过程为先超重，后失重，故B错误； C.0.5s时，为下蹲过程中乡下加速最快的时刻，并非下蹲到了最低点，故C错误； D.3s时为超重状态，因此加速度方向竖直向上，故D正确。 故选：D。 题型5等时圆模型的应用 13. （2023•迎泽区校级二模）如图所示，竖直平面内半径R ＝10m的圆弧AO与半径R ＝2.5m的圆弧 1 2 BO在最低点O相切。两段光滑的直轨道的一端在O点平滑连接，另一端分别在两圆弧上且等高。一个小球 从左侧直轨道的最高点A由静止开始沿直轨道下滑，经过O点后沿右侧直轨道上滑至最高点B，不考虑小球 在O点的机械能损失，重力加速度g取10m/s2。则在此过程中小球运动的时间为（ ） A．1.5 s B．2.0 s C．3.0 s D．3.5 s 【解答】解：由于AO对应的圆的半径为R ，通过O点作出AO所在圆的直径，如图所示： 1 根据图中几何关系可得：AO＝2R sinθ 1 mgsinθ 小球在AO上运动的加速度大小为：a = =gsinθ 1 m 1 设小球在AO上运动的时间为t ，则有：AO= a t2 1 2 1 1 √4R 联立解得：t = 1 1 g 小球在OB段运动过程中，逆向分析也可以看作是初速度为零的匀加速直线运动，同理分析可得小球在 OB段 √4R 运动的时间为：t = 2 2 g在此过程中小球运动的时间为：t＝t +t 1 2 联立并代入数据解得：t＝3.0s，故C正确、ABD错误。 故选：C。 14. （2023•渭南一模）如图所示，OA、OB是竖直面内两根固定的光滑细杆，O、A、B位于同一圆周上， OB为圆的直径。每根杆上都套着一个小滑环（图中未画出），两个滑环都从O点无初速释放，用t 、t 分别 1 2 表B示滑环到达A、B所用的时间，则（ ） A．t ＝t 1 2 B．t ＜t 1 2 C．t ＞t 1 2 D．无法比较t 、t 的大小 1 2 【解答】解：如下图所示，以O点为最高点，取合适直径作经过B点的等时圆，可得A点在所做等时圆的外边。 根据等时圆规律，小滑环从O到C与从O到B所用时间相等，均为t ，图示位移OA＞OC，可得t ＞t ，故C 2 1 2 正确，ABD错误。 故选：C。 15. 如图所示，在斜面上同一竖直面内有四条光滑细杆，其中 OA杆竖直放置，OB杆与OD杆等长，OC 杆与斜面垂直放置，每根杆上都套着一个小滑环（图中未画出），四个环分别从 O点由静止释放，沿OA、 OB、OC、OD滑到斜面上所用的时间依次为t 、t 、t 、t下列关系正确的是（ ） 1 2 3A．t ＜t B．t ＞t C．t ＝t D．t ＜t 1 2 1 3 2 4 2 4 【解答】解：以OA为直径画圆，根据等时圆模型，对小滑环，受重力和支持力，将重力沿杆的方向和垂直杆 的方向正交分解，根据牛顿第二定律得小滑环做初速为零的匀加速直线运动的加速度为a＝gcosθ（θ为杆与竖 直方向的夹角） 由图中的直角三角形可知，小滑环的位移S＝2Rcosθ， 1 根据位移—时间关系可得：S= at2 ， 2 √2S √4Rcosθ √4R 所以t= = = ，t与θ无关， a gcosθ g 可知从圆上最高点沿任意一条弦滑到底所用时间相同，故沿OA和OC滑到底的时间相同，即t ＝t ，OB 1 3 不是一条完整的弦，时间最短，即t ＞t ，OD长度超过一条弦，时间最长，即t ＜t故ABC错误，D正 1 2 2 确。 故选：D。 题型6动力学图像问题 16. （2024•镇海区校级开学）如图甲所示水平地面上固定一足够长的光滑斜面，斜面顶端有一理想定滑 轮，轻绳跨过滑轮，绳两端分别连接小物块A和B。保持A的质量不变，改变B的质量m，当B的质量连续 改变时，得到A的加速度a随B的质量m变化的图线如图乙所示，设加速度沿斜面向上的方向为正方向，空 气阻力不计，重力加速度g取9.8m/s2，斜面的倾角为θ。下列说法正确的是（ ） A．若θ已知，可求出A的质量 B．若θ未知，则无法求出图乙中a 的值 1C．若θ已知，可求出图乙中a 的值 2 D．若θ已知，可求出图乙中m 的值 0 【解答】解：AD、由图乙知，m＝m 时，A的加速度a＝0，则此时受力平衡，对A、B分析得m g＝m gsinθ， 0 0 A 由于m 未知，所以不能求出m 的大小，m 未知，m 不可求，故AD错误； 0 A A 0 B、设绳的拉力为T，加速度大小为a，m任意时，对B使用牛顿定律分析有mg﹣T＝ma m−m sinθ 对A分析T﹣m gsinθ＝m a，联立二式得a= A g，当m趋向无穷大时，a趋向于g，所以a ＝g，即a A A m+m 1 1 A 与θ无关，故B错误； C、a＝a 时，m＝0，即绳对A的拉力为零，有m gsinθ＝m a ，解得a ＝gsinθ，θ已知，所以可以求a 的值， 2 A A 2 2 2 故C正确。 故选：C。 17. 如图甲所示，光滑水平面上静置一足够长的木板Q，小滑块P放置于其上表面，木板Q在水平拉力F 作用下，加速度a随拉力F变化的关系图像如图乙所示，则小滑块P的质量为（ ） A．2kg B．3kg C．4kg D．5kg 【解答】解：刚开始PQ两个一起做加速运动，根据牛顿第二定律F＝（m +m ）a P Q 结合图像斜率m +m ＝3kg P Q 当加速度大于等于2m/s2，PQ分开各自加速，设Q受到的摩擦力大小为f，根据牛顿第二定律 F﹣f＝m a Q 结合图像斜率m ＝1kg Q 联立可得m ＝2kg，故A正确，BCD错误。 P 故选：A。 18. （多选）（2022秋•浦东新区校级期末）物块a、b中间用一根轻质弹簧相接，放在光滑水平面上， m ＝3kg，如图甲所示。开始时两物块均静止，弹簧处于原长，t＝0时对物块a施加水平向右的恒力F。t＝2s a 时撤去，在0～2s内两物体的加速度随时间变化的情况如图乙所示。弹簧始终处于弹性限度内，整个运动过 程中以下分析正确的是（ ）A．0～2s内物块a与物块b的距离一直在减小 B．物块b的质量为m ＝2kg b C．撤去F瞬间，a的加速度大小为0.8m/s2 D．若F不撤去，则2s后两物块将一起做匀加速运动 【解答】解：A、根据a﹣t图像与坐标轴所围的面积表示速度的变化量，由图像可知0～2s内a的速度一直大于 b的速度，物块a与物块b的距离一直在增大，故A错误； B、t＝0时，弹簧弹力为零，对a根据牛顿第二定律可得F＝m a ＝3×2.0N＝6N a 0 t＝2s时，a、b整体加速度相同，对整体根据牛顿第二定律可得F＝（m +m ）a ＝6N a b 1 代入数据解得：m ＝2kg，故B正确； b C、2s时，对b根据牛顿第二定律可得弹簧弹力大小为F ＝m a ＝2×1.2N＝2.4N x b 1 F 2.4 撤去F瞬间，弹簧弹力不会突变，此时a的加速度大小为a '= x = m/s2=0.8m/s2 ，故C正确； 1 m 3 a D、a﹣t图像与坐标轴所围的面积表示速度的变化量，从图像可看出，t＝2s时a的速度大于b的速度，所以若 此时不撤去F，弹簧在之后的一段时间内会继续伸长，a的加速度减小，b的加速度增大，并不能一起做匀加速 运动，故D错误。 故选：BC。第 8 讲 曲线运动 运动的合成与分解 1.掌握曲线运动的概念、特点及条件. 2.掌握运动的合成与分解法则． 考点一 物体做曲线运动的条件及轨迹 1．曲线运动(1)速度的方向：质点在某一点的速度方向，沿曲线在这一点的切线方向． (2)运动的性质：做曲线运动的物体，速度的方向时刻在改变，所以曲线运动一定是变速运动． (3)曲线运动的条件：物体所受合外力的方向跟它的速度方向不在同一条直线上或它的加速度方向与速度方向不在 同一条直线上． 2．合外力方向与轨迹的关系 物体做曲线运动的轨迹一定夹在合外力方向与速度方向之间，速度方向与轨迹相切，合外力方向指向轨迹的 “凹”侧． 3．速率变化情况判断 (1)当合外力方向与速度方向的夹角为锐角时，物体的速率增大； (2)当合外力方向与速度方向的夹角为钝角时，物体的速率减小； (3)当合外力方向与速度方向垂直时，物体的速率不变． [例题1] （2024•重庆模拟）如图所示，“嫦娥号”探月卫星在由地球飞向月球时，沿曲线从M点向N点 飞行的过程中，速度逐渐减小，在此过程中探月卫星所受合力方向可能是下列图中的（ ） A． B． C． D． 【解答】解：“嫦娥号”探月卫星从M点运动到N，做曲线运动，速度逐渐减小，故合力指向指向凹侧，且合 力与速度的方向的夹角要大于90°，故ABC错误，D正确。 故选：D。 [例题2] （2024•金台区模拟）我国研制的“威龙”J﹣20是高性能五代歼击机，它在空中能做连续的开 普勒抛物线飞行，飞机飞行的轨迹从左向右运动，图中各点的速度与飞机所受合力的方向可能正确的 （ ） A．a点 B．b点 C．c点 D．d点 【解答】解：由于曲线运动的速度方向沿轨迹上该点的切线方向，合外力应指向曲线的内侧，故 ACD错误，B 正确 故选：B。[例题3] （2023•黄埔区三模）如图所示，乒乓球从斜面上滚下后在水平桌面上沿直线运动。在与乒乓球 运动路线垂直的方向上横放一个纸筒（纸筒开口略大于乒乓球直径）。人趴在桌子边沿并鼓起嘴巴正对纸筒 口，当乒乓球经过筒口时，对着乒乓球向筒口吹气，则乒乓球被吹后（ ） A．保持原运动方向继续前进 B．一定能沿吹气方向进入纸筒 C．偏离原运动方向滚向纸筒左侧 D．偏离原运动方向滚向纸筒右侧 【解答】解：一开始乒乓球向右运动，当乒乓球受到沿纸筒方向的吹气的力后，乒乓球参与了两个方向的分运 动，会偏离原运动方向滚向纸筒右侧；由于惯性，乒乓球不可能吹气方向进入纸筒。故ABC错误，D正确。 故选：D。 考点二 运动的合成及运动性质分析 1．遵循的法则： 位移、速度、加速度都是矢量，故它们的合成与分解都遵循平行四边形定则． 2．合运动与分运动的关系 (1)等时性:合运动和分运动经历的时间相等，即同时开始、同时进行、同时停止． (2)独立性:一个物体同时参与几个分运动，各分运动独立进行，不受其他运动的影响． (3)等效性:各分运动的规律叠加起来与合运动的规律有完全相同的效果． 3．合运动的性质判断 4．两个直线运动的合运动性质的判断 标准：看合初速度方向与合加速度方向是否共线. 两个互成角度的分运动 合运动的性质 两个匀速直线运动 匀速直线运动 一个匀速直线运动、一个匀变速直线运 匀变速曲线运动 动 两个初速度为零的匀加速直线运动 匀加速直线运动 两个初速度不为零的匀变速直线运动 如果v 与a 共线，为匀变速直线运动 合 合[例题4] （2024•惠州一模）我国的风洞技术处于世界领先地位。如图所示，在某次风洞实验中，一质量 为m的轻质小球，在恒定的风力作用下先后以相同的速度大小v经过a、b两点，速度方向与a、b连线的夹 角α、β均为45°。已知a、b连线长为d，小球的重力忽略不计。则小球从a点运动到b点过程中，下列说法 正确的是（ ） A．风力方向与a、b连线平行 √2d B．所用时间为 v C．小球做匀速圆周运动 2mv2 D．风力大小为 d 【解答】解：A、由题意可知小球做匀变速曲线运动，根据加速度的定义可知加速度方向移动和速度变化量的 方向相同，根据几何关系可知加速度（或合力）方向垂直于a、b连线，如图， 所以风力方向垂直于a、b连线，故A错误； √2 B、小球的速度沿a、b连线方向的分速度为：v ＝vsin45°= v 1 2 d d √2d t= = = 由于沿ab方向是做匀速直线运动，所以a运动到b的时间为： v √2 v ，故B正确； 1 v 2 C、小球受到恒定风力的作用，做匀变速曲线运动。而匀速圆周运动必须受到始终指向圆心方向的合力，小球 不可能做匀速圆周运动，故C错误； D、根据平行四边形定则和数学知识可得：沿风力的方向从a点运动到b点的速度变化量为： Δv风 ＝vsinβ﹣（﹣vsinα）＝vsin45°+vcos45°=√2v Δv √2v v2 a= 风= = 那么加速度为： t √2d d vmv2 根据牛顿第二定律，从a点运动到b点的风力为：F=ma= ，故D错误。 d 故选：B。 [例题5] （2024•沈阳二模）风洞实验是进行空气动力学研究的重要方法。如图所示，将小球从A点以某 一速度v 水平向左抛出，经过一段时间，小球运动到A点正下方的B点，O点是轨迹的最左端，风对小球的 0 作用力水平向右，大小恒定。则小球速度最小时位于（ ） A．A点 B．O点 C．轨迹AO之间的某一点 D．轨迹OB之间的某一点 【解答】解：风对小球的力恒定，说明水平方向的加速度恒定，设水平方向加速度为a，则有v ＝v ﹣at x 0 竖直方向受重力加速度影响，做匀加速运动，有v ＝gt y 合速度为v=√v2+v2=√g2t2+v2+a2t2−2v at=√(g2+a2 )t2−2v at+v2 x y 0 0 0 0 −2v a v a v a 根号内为二次函数，其对称轴为t = 0 = 0 ，说明当t= 0 时，合速度有最小值 −2⋅(g2+a2 ) g2+a2 g2+a2 v v a v a 当v ＝v ﹣at＝0时，t= 0= 0 ＞ 0 ，说明最小速度出现在AO轨迹之间的某一点，故C正确，ABD错 x 0 a a2 g2+a2 误； 故选：C。 [例题6] （2024•天河区一模）如图为自动控制货品运动的智能传送带，其奥秘在于面板上蜂窝状的小正 六边形部件，每个部件上有三个导向轮A、B、C，在单个方向轮子的作用下，货品可获得与导向轮同向的速 度v，若此时仅控制A、C两个方向的轮子同时按图示箭头方向等速转动，则货品获得的速度大小为（ ） A．v B．√2v C．√3v D．2v 【解答】解：物体参与了两个方向的运动，两个分速度的夹角为60°，根据速度合成可知，合速度为v =2vcos30°=√3v 实际 故ABD错误，C正确。 故选：C。 考点三 小船渡河模型 小船渡河问题分析 (1)船的实际运动是水流的运动和船相对静水的运动的合运动． (2)三种速度：v(船在静水中的速度)、v(水流速度)、v(船的实际速度)． 1 2 (3)三种情景 ①过河时间最短：船头正对河岸时，渡河时间最短，t ＝(d为河宽)． 短 ②过河路径最短(vv 时)：合速度 2 1 不可能垂直于河岸，无法垂直渡河．确定方法如下：如图所示，以v 矢量末端为圆心，以v 矢量的大小为半径画 2 1 弧，从v 矢量的始端向圆弧作切线，则合速度沿此切线方向航程最短．由图可知：cos α＝，最短航程：s ＝＝d. 2 短 [例题7] （2024•肇庆二模）下列说法正确的是（ ） A．人在松软的土地上下陷时，人对地面的压力大于地面对人的支持力 B．“强弩之末，势不能穿鲁缟”，是因为弩箭的惯性减小了 C．跳高运动员在越杆时处于平衡状态 D．船相对于静水的速度大于河水流速时，船过河的最短路程等于河的宽度 【解答】解：A．人对地面的压力与地面对人的支持力是作用力与反作用力，二者大小始终相等，故A错误； B．质量是惯性大小的量度，与速度无关，故B错误； C．跳高运动员在越杆时受重力作用，受到的力不等于零，所以不是平衡状态，故C错误； D．船相对于静水的速度大于河水流速时，合速度可以垂直于河岸，船过河的最短路程等于河的宽度，故D正 确。 故选：D。 [例题8] （2023•海南模拟）一小船在静水中的速度为3m/s，它在一条河宽150m，流速为5m/s的河流中 渡河，则下列说法正确的是（ ）A．小船渡河时间不少于60s B．小船以最短时间渡河时，它沿水流方向的位移大小为150m C．小船以最短位移渡河时，位移大小为250m D．小船以最短位移渡河时，时间为60s d = 【解答】解：AD、当船头垂直对岸行驶时时间最短，故最短时间是t 代入数据解得t ＝50s，故AD错 min v min 船 误； B、船以最短时间渡河，它沿水流方向位移大小为x＝v水t代入数据解得x＝250m，故B错误； C 、 因 船 速 小 于 水 速 ， 故 当 合 速 度 方 向 与 船 速 垂 直 时 ， 渡 河 位 移 最 短 ， 如 图 所 示 v 3 d 设此时合速度的方向与河岸的夹角为θ，sinθ= 船= ，则渡河的最小位移为x= 代入数据解得x＝250m， v 5 sinθ 水 故C正确； 故选：C。 [例题9] （2023•南岗区校级三模）如图所示，以岸边O点为原点建立空间直角坐标系，x轴沿河岸方向、 y轴垂直河岸方向、z轴竖直向上。水速恒为v ＝5m/s，方向沿x轴正向。t＝0时刻开始，某船保持船头始终 x 朝向y轴正方向运动至江心，船在y方向上的初速度为零，加速度为a =4m/s2。船在x轴方向上的速度始 1 终与水速相同。在t＝5s时，船员相对船体以v ＝10m/s的速度将一个小石块垂直向上抛出，忽略空气阻力， z 重力加速度取g＝10m/s2。求： （1）t＝5s时船的位置坐标（x ，y ，z ）； 1 1 1 （2）石块到达最高点时的位置坐标（x ，y ，z ）。 2 2 2 1 【解答】解：（1）沿y方向做匀加速直线运动，则：y = a t2 1 2 y代入已知数据解得：y ＝50m 1 x方向做匀速直线运动，则x ＝v t 1 x 代入已知条件解得：x ＝25m 1 所以t＝5s时船的位置坐标为（25m，50m，0） （2）石块扔出瞬间，此时：v ＝a t＝4×5m/s＝20m/s y y v 10 石块到达最高点的时间：t = z= s=1s 2 g 10 此时x方向的位移：x ＝v （t+t ）＝5（5+1）m＝30m 2 x 2 y方向的位移：y ＝y +v t ＝50m+20×1m＝70m 2 1 y2 1 1 沿z方向的位移：z = gt2= ×10×12 m＝5m 2 2 2 2 所以石块到达最高点时的位置坐标（30m，70m，5m） 答：（1）t＝5s时船的位置坐标（25m，50m，0）； （2）石块到达最高点时的位置坐标（30m，70m，5m）。 考点四 绳(杆)端速度分解模型 1．模型特点 沿绳(或杆)方向的速度分量大小相等． 2．思路与方法 合运动→绳拉物体的实际运动速度v 分运动→ 方法：v 与v 的合成遵循平行四边形定则． 1 2 3．解题的原则： 把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相等求解．常见 的模型如图8所示．[例题10]（2024•碑林区校级模拟）甲、乙两光滑小球（均可视为质点）用轻直杆连接，乙球处于粗糙水 平地面上，甲球紧靠在粗糙的竖直墙壁上，初始时轻杆竖直，杆长为4m。施加微小的扰动，使得乙球沿水平 地面向右滑动，当乙球距离起点3m时，下列说法正确的是（ ） A．甲、乙两球的速度大小之比为4：3 B．甲、乙两球的速度大小之比为3：√7 C．甲球即将落地时，乙球的速度与甲球的速度大小相等 D．甲球即将落地时，乙球的速度达到最大 3 √7 【解答】解：AB、当乙球距离起点3m时，设轻杆与竖直方向夹角为θ，根据几何知识可得sinθ= ，cosθ= 4 4 将两球的速度分别沿杆和垂直于杆的方向进行分解，如图所示： 则甲的速度v 1 在沿杆方向的分量为v 1杆 ＝v 1 cosθ，乙的速度v 2 在沿杆方向的分量为v 2杆 ＝v 2 sinθ，结合v 1杆 ＝v 2杆 ， 解得甲、乙两球的速度大小之比为 v ：v ＝3：√7，故A错误，B正确； 1 2 CD、当甲球即将落地时，θ＝90°，此时甲球的速度达到最大，根据v cosθ＝v sinθ，得乙球的速度v ＝0，故 1 2 2 CD错误； 故选：B。 [例题11] （2023•琼山区校级三模）如图所示，将质量为2m的重物悬挂在轻绳的一端，轻绳的另一端系 一质量为m的小环，小环套在竖直固定的光滑直杆上，光滑定滑轮与直杆的距离为 d。现将小环从与定滑轮 等高的A处由静止释放，当小环沿直杆下滑距离也为d时（图中B处），下列说法正确的是（ ）A．环减少的机械能大于重物增加的机械能 B．小环到达B处时，重物上升的高度也为d √2 C．环在B处的速度与重物上升的速度大小之比为 2 D．环在B处的速度为v=√(3−2√2)gd 【解答】解：A、由于小环和重物只有重力做功，则系统机械能守恒，所以环减少的机械能等于重物增加的机 械能，故A错误； d B、结合几何关系可知，重物上升的高度：h= −d＝（√2−1）d，故B错误； cos45° C、两个物体沿着绳子方向的分速度，故：v环cos45°＝v G ，故环在B处的速度与重物上升的速度大小之比为√2： 1，故C错误； 1 1 D、小环和重物组成的系统机械能守恒，故：mgd = 2 mv 环 2+ 2 （2m）v G 2 +（2m）gh；联立解得：v 环 =√(3−2√2)gd，故D正确。 故选：D。 [例题12]（2023•泰和县校级一模）质量为m的物体P置于倾角为θ 的固定光滑斜面上，轻细绳跨过光滑 1 定滑轮分别连接着P与小车，P与滑轮间的细绳平行于斜面，（本资料来自于公众号：屋里学家）小车以速率 v水平向右做匀速直线运动。已知重力加速度为 g。当小车和滑轮间的细绳与水平方向成夹角θ 时（如图）， 2 下列判断正确的是（ ） A．P的速率为v B．P的速率为vsinθ 2 C．运动过程中P处于超重状态 D．线的拉力始终等于mgsinθ 1 【解答】解：AB、将小车的速度沿细绳和垂直细绳方向分解，如图所示：可知沿细绳方向分速度表达式为v ＝v ＝vcosθ ，故A、B错误； P 2 2 CD、由于小车往右运动，可知θ 逐渐减小，因此vcosθ 在逐渐增大，所以P往上做加速运动，故C正确，D错 2 2 误。 故选：C。 题型1曲线运动条件及特点 1. （2023•昌平区模拟）关于曲线运动，下列说法正确的是（ ） A．曲线运动的速度方向可以不变 B．匀变速曲线运动任意相等时间内速度的变化量相同 C．速率恒定的曲线运动，任意相等时间内速度的变化量相同 D．物体受到的合外力持续为零时，物体仍可以做曲线运动 【解答】解：A、曲线运动的速度方向一定变，故A错误； B、匀变速曲线运动，加速度不变，即相等时间，速度变化量相同，故B正确； C、曲线运动速度的方向是变化的，速率恒定的曲线运动受到的合外力的方向一定与速度的方向始终垂直，则 合外力的方向必定是变化的，则任意相等时间内速度的变化量一定不相同，故C错误； D、物体做曲线运动的条件是物体所受的合外力和它速度方向不在同一直线上，所以物体受到的合外力持续为 零时，物体不可能做曲线运动，故D错误。 故选：B。 2. （2023•海口一模）如图所示，这是质点只在重力作用下所做的曲线运动轨迹的示意图，已知B为轨 迹的最高点，则下列说法正确的是（ ） A．质点在B点时的加速度方向与速度方向不垂直B．质点在A点时的加速度比在B点时的加速度小 C．质点在C点时的速率大于在B点时的速率 D．质点从A点到C点，加速度方向与速度方向的夹角先减小后增大，速度先增大后减小 【解答】解：AB、质点受重力作用做匀变速曲线运动，在最高点B时，速度方向与重力加速度的方向垂直，整 个过程重力加速度保持不变，故AB错误； C、质点从B点到C点，加速度方向与速度方向夹角小于90°，因此该过程质点的速度增大，所以质点在C点时 的速率大于在B点时的速率，故C正确； D、质点只受重力作用，加速度方向始终竖直向下，质点的速度方向沿运动轨迹的切线方向，质点从 A点到C 点，加速度方向与速度方向的夹角一直减小；从A到B的过程中，加速度与速度方向的夹角大于90°，质点做 减速运动，从B到C的过程中，加速度与速度方向的夹角小于90°，质点做加速运动，速度增大，因此质点从 A到C的过程中，速度先减小后增大，故D错误。 故选：C。 题型2曲线运动速率的变化 3. （2023•鞍山一模）“歼﹣20”再次闪亮登场2022珠海航展。如图所示，战机先水平向右，再沿曲线 ab向上，最后沿陡斜线直入云霄。设飞行路径在同一竖直面内，飞行速率不变，则沿ab段曲线飞行时，战机 （ ） A．所受合外力不变 B．所受合外力方向竖直向上 C．竖直方向的分速度不变 D．水平方向的分速度逐渐减小 【解答】解：AB、战机飞行速率不变，合力方向始终与速度方向垂直，即指向圆心，所受合外力方向不断变化， 不是竖直向上的，故AB错误； C、飞机速度大小不变，与水平方向的倾角θ增大，可得竖直分速度为v ＝vsinθ增大，即竖直方向的分速度逐 y 渐增大，故C错误； D、飞机速度大小不变，与水平方向的倾角θ增大，可得水平分速度为v ＝vcosθ减小，即水平方向的分速度减 x小，故D正确。 故选：D。 4. （多选）（2022•海拉尔区校级四模）冰壶比赛中投壶手在投出冰壶时会带有一定的旋转（自旋）， 擦冰手在冰壶运动的前方高速摩擦冰面（刷冰），减小冰壶前侧受到的摩擦力，可使冰壶做曲线运动。在图 示的各图中，圆表示冰壶，ω表示冰壶自旋的方向，v表示冰壶前进的方向，则在刷冰的过程中，冰壶运动的 轨迹（虚线表示）可能正确的是（ ） A． B． C． D． 【解答】解：由题意可知，擦冰手在冰壶运动的前方高速摩擦冰面（刷冰），减小冰壶前侧受到的摩擦力，而 后侧所受摩擦力几乎不变，若冰壶按逆时针方向旋转，则沿速度垂直的方向，摩擦力的合力向左，则冰壶运动 轨迹将向左偏转；同理若冰壶按顺时针方向旋转，冰壶运动轨迹向右偏转。故AD正确，BC错误。 故选：AD。 题型3生活中的运动合成与分解 5. （2024•海门区校级二模）如图所示，光滑水平桌面上，一小球以速度v向右匀速运动，当它经过靠 近桌边的竖直木板ad边正前方时，木板开始做自由落体运动。若木板开始运动时，cd边与桌面相齐，则小球 在木板．上的投影轨迹是（ ）A． B． C． D． 【解答】解：投影在水平方向做匀速直线运动，竖直方向上相对于木板向上做加速运动，故小球的合速度应偏 向上方，同时加速度指向曲线的内侧，故轨迹应向上；故ACD错误，B正确； 故选：B。 6. （多选）（2024•佛山二模）如图所示，在一条玻璃生产线上，宽3m的待切割玻璃板以0.4m/s的速 度向前匀速平移。在切割工序处，金刚石切割刀的移动速度为0.5m/s，下列说法正确的是（ ） A．切割一块矩形玻璃需要10s B．切割得到的矩形玻璃长为2.4m C．切割刀的移动轨迹与玻璃板平移方向夹角为37°，可使割下的玻璃板呈矩形 D．切割刀的移动轨迹与玻璃板平移方向夹角为143°，可使割下的玻璃板呈矩形 【解答】解：设金刚钻割刀的轨道方向与玻璃板运动的速度方向的夹角为 θ，可使割下的玻璃板呈矩形，如图 所示： 其中v＝0.5m/s，v ＝0.4m/s，根据几何关系可得： 1 v 0.4 因为合速度的方向与玻璃板垂直，根据平行四边形定则得：cosθ= 1= =0.8 v 0.5 则有：θ＝37° 垂直于玻璃运动方向的速度大小为：v ＝vsinθ，解得：v ＝0.3m/s。 2 2 d 3 A、切割一块矩形玻璃需要的时间为：t = = s＝10s，故A正确； v 0.3 2 B、切割得到的矩形玻璃长为：L＝v t＝0.4×10m＝4m，故B错误； 1 CD、根据以上分析可知，切割刀的移动轨迹与玻璃板平移方向夹角为37°，可使割下的玻璃板呈矩形，故C正 确、D错误。故选：AC。 题型4有关运动合成与分解的图像问题 7. （2023•浙江模拟）由于空气阻力的影响，炮弹的实际飞行轨迹不是抛物线，而是“弹道曲线”，如 图中实线所示，图中虚线为不考虑空气阻力情况下炮弹的理想运动轨迹。O、a、b、c、d为弹道曲线上的五 点，其中O点为发射点，d点为落地点，b点为轨迹的最高点，a、c为运动过程中经过的距地面高度相等的两 点，重力加速度为g。下列说法正确的是（ ） A．炮弹到达最高点b时的加速度为g B．炮弹经过c点时的加速度方向沿该点切线斜向上 C．炮弹经过a点时加速度的竖直分量大于g D．炮弹由a点运动到b点的时间与由b点运动到c点的时间相等 【解答】解：A．在最高点b，炮弹除了受重力还受到向后的空气阻力，加速度大于g，故A错误； B．根据曲线运动特点，炮弹经过c点时加速度方向一定指向轨迹凹侧，故B错误； C．炮弹经过a点时，受空气阻力和重力共同作用，空气阻力方向与速度方向相反斜向左下方，根据牛顿第二定 律，加速度的竖直分量由重力和空气阻力竖直分力相加得出，所以炮弹经过 a点时加速度的竖直分量大于g， 故C正确； D．设炮弹由a点运动到b点过程中，受阻力平均竖直分量为f ，由b点运动到c点过程中，受阻力平均竖直分 1 mg+f 量为f ，根据牛顿第二定律，则前、后两个过程炮弹竖直平均加速度大小分别为a = 1 2 1 m mg−f a = 2＜a 2 m 1 根据运动学规律，炮弹由a点运动到b点时间小于由b点运动到c点时间，故D错误。 故选：C。 8. （2024•吉林一模）质量为2kg的质点在xy平面上做曲线运动，在x方向的速度图象和y方向的位移 图象如图所示，下列说法正确的是（ ）A．质点的初速度为3 m/s B．质点所受的合外力为3 N C．质点初速度的方向与合外力方向垂直 D．2 s末质点速度大小为6 m/s Δy 0−8 【解答】解：A、x 轴方向初速度为 v ＝3m/s，y 轴方向初速度 v = = =−4m/s，质点的初速度 v x y Δt 2 0 =√v2+v2=√32+42=5m/s。故A错误。 x y Δv 6−3 B、x轴方向的加速度a= x = =1.5m/s2，质点的合力F合 ＝ma＝3N．故B正确。 Δt 2 C、合力沿x轴方向，而初速度方向既不在x轴，也不在y轴方向，质点初速度的方向与合外力方向不垂直。 故C错误。 D、由图可知，2 s 末质点速度 x 方向的大小为 6 m/s，而 y 方向的速度仍然是﹣4m/s，所以合速度是 √62+42=√52m/s。故D错误。 故选：B。 题型5小船渡河最短时间问题 9. （多选）（2023•上饶模拟）一艘小船正在渡河，如图所示，在到达离河对岸 60m处的P点时，其下 游80m处有一危险水域，已知船在静水中的最大速度为6m/s，水流的速度大小为5m/s，P点离另一河岸的距 离大于100m，下列说法正确的是（ ） A．小船以最短时间渡河时，可以安全到达河岸B．小船以最短时间渡河时，不能安全到达河岸 C．小船渡河的位移可能为60m D．小船渡河的位移不可能为100m 【解答】解：AB．根据题意可知，当船头正对河岸且以最大的静水速度航行时，渡河时间最短，最短时间为 d 60 t min = v = 6 s=10s，此时，船沿河岸移动的距离为x＝v水t min ＝5×10m＝50m＜80m，不会到达危险水域，故 船 小船以最短时间渡河时，可以安全到达河岸，故B错误，A正确； C．船在静水中速度大于水流速度，则可以通过调整船头方向，让船速度斜向上，让船的合速度方向正对河岸， 此时渡河位移最短，最短距离为河宽60m，故C正确； D．通过调整船头方向，让船的合速度方向指向上游时，角度合适，位移可能是 100m，此时还没有到达危险水 域，能保证小船的安全，故D错误。 故选：AC。 10. （2022•桃城区校级模拟）某小船在河宽为d，水速恒定为v的河中渡河，第一次用最短时间从渡口 向对岸开去，此时小船在静水中航行的速度为v ，所用时间为t ；第二次用最短航程渡河从同一渡口向对岸 1 1 开去，此时小船在静水中航行的速度为v ，所用时间为t ，结果两次恰好抵达对岸的同一地点，则（ ） 2 2 d A．第一次所用时间t = 1 v d = B．第二次所用时间t 2 v 2 v 2 C．两次渡河的位移大小之比为 v 1 t v2 D．两次渡河所用时间之比 1= 2 t v2 2 1 d d = t = v 1 v 静 1 【解答】解：A．两次渡河时如图 渡河最短时间t ，所以 ， 故A错误； v v B．第一次渡河有tanα= 1，第二次渡河时有： 2=sinα， v v1 v 所以 = 1 ， cosα v 2 d 第二次渡河时间为：t = ，故B错误； 2 v cosα 2 C．根据图形可知两次位移之比为1：1，故C错误； t v cosα v2 D．两次时间之比 1= 2 = 2 ，故D正确； t v v2 2 1 1 故选：D。 题型6小船渡河最短距离问题 11. （2022•市中区校级模拟）一条平直小河的河水由西向东流，水流速度的大小为v水 ＝4m/s，让小船 船头垂直河岸由南向北渡河，已知小船在垂直河岸方向运动的规律满足x＝6t﹣0.05t2，且小船刚好到达河对 岸，则小船在渡河的这段时间内的运动情况，下列说法正确的是（ ） A．小船渡河的轨迹为直线 B．小船在河水中40s时的速度为√41m/s C．小船在河水中40s时的位移为160m D．小船到达河对岸时沿河岸方向运动的位移为240m 1 【解答】解：将小船在垂直河岸方向运动的规律 x＝6t﹣0.05t2，与匀变速直线运动的公式：x=v t+ at2 比较 0 2 可知，小船沿垂直河岸方向运动的初速度：v船0 ＝6m/s，加速度：a＝﹣0.1m/s2；可知小船在垂直河岸方向做匀 减速直线运动； A、小船在垂直河岸方向上做匀减速直线运动，在沿河岸方向上做匀速直线运动，合加速度的方向与合速度方 向不在同一条直线上，做曲线运动，故A错误； B、小船在河水中在垂直河岸方向的速度：v船 ＝v船0 +at＝6m/s﹣0.1×40m/s＝2m/s 船运动的合速度：v=√v2 +v2 =√42+22m/s=2√5m/s，故B错误； 水 船 1 1 C、40s内船沿垂直河岸方向的位移：x=v t+ at2=6×40m+ ×(−0.1)×402 m＝160m，沿河岸方向的位 船0 2 2 移：y＝v水t＝4×40m＝160m，所以船的合位移：s=√x2+ y2=√1602+1602m=160√2m，故C错误；0−v 0−6 D、小船刚好到达河对岸，则到达对岸时垂直于河岸方向的速度为零，所以运动的时间：t = 船0= s 0 a −0.1 ＝60s，该过程中小船沿河岸方向运动的位移为：y′＝v水t 0 ＝4×60m＝240m，故D正确。 故选：D。 题型7绳类关联速度 12. （2023•重庆模拟）如图所示，物体A和小车用轻绳连接在一起，小车以速度v 向右匀速运动。当小 0 车运动到图示位置时，轻绳与水平方向的夹角为θ，关于此时物体A的运动情况的描述正确的是（ ） A．物体A减速上升 B．物体A的速度大小v ＝v A 0 C．物体A的速度大小v ＝v sinθ A 0 D．物体A的速度大小v ＝v cosθ A 0 【解答】解：将小车的速度沿绳子方向和垂直于绳子方向进行分解， 沿绳子方向的分速度等于A的速度，则：v ＝v cosθ， A 0 小车向右做匀速直线运动，则θ减小，则A的速度增大，A做加速运动，故D正确，ABC错误。 故选：D。 13. （2023•凯里市校级模拟）如图所示，质量为m的木块a放置在倾角为α的固定斜面上，通过一根不 可伸长的细线绕过固定在斜面上的轻滑轮与质量为m、套在杆上的小球b相连，小球以速率v向左匀速运动， 不计空气阻力和一切摩擦力，重力加速度为g。当细线与水平杆的夹角为β时（ ） A．木块a的速度大小为vv B．木块a的速度大小为 cosβ C．细线的拉力大于mgsinα D．细线的拉力小于mgsinα 【解答】解：AB、将小球b的速度分解为沿绳方向的分速度v 和垂直于绳方向的分速度v 1 2 由几何关系得，木块a的速度大小等于v ＝vcosβ 1 故AB错误； CD、小球b向左做匀速直线运动，β逐渐减小，cosβ逐渐增大，则木块a的速度逐渐增大，即木块a做加速运 动，对木块受力分析，沿斜面方向，细线的拉力大于mgsinα，故C正确，D错误。 故选：C。 题型8杆类关联速度 14. （2023•浙江模拟）如图所示，斯特林发动机的机械装置可以将圆周运动转化为直线上的往复运动。 连杆AB，OB可绕图中A、B、O三处的转轴转动，连杆OB长为R，连杆AB长为L（L＞R），当OB杆以 角速度ω逆时针匀速转动时，滑块在水平横杆上左右滑动，连杆 AB与水平方向夹角为α，AB杆与OB杆的 夹角为β。在滑块向左滑动过程中（ ） A．滑块A从右向左先做加速度减小的加速运动，后做加速度减小的减速运动 B．当OB杆与OA垂直时，滑块的速度最大 R2ω C．当OB杆与OA垂直时，滑块的速度大小为 LRω√L2+R2 D．当β＝90°时，滑块的速度大小为 L 【解答】解：设滑块的速度（合速度）大小为v，沿水平方向，如图将A点的速度分解为沿着杆的分速度和垂 直杆的分速度 根据运动的合成与分解可知，沿杆方向的分速度： v ＝vcosα 1 BB点做圆周运动，实际速度是圆周运动的线速度，可以分解为沿杆方向的分速度和垂直于杆方向的分速度，如 图设B的线速度为v'，则 沿杆的分速度： v' ＝V'cosθ＝V'cos（90°﹣β）＝V'sinβ 1 V'＝ωR 又二者沿杆方向的分速度是相等的，即v ＝v' 1 1 ωRsinβ 联立可得v= cosα R S 在△AOB中，由正弦定理得 = OA sinα sinβ 解得v＝ωs tanα OA A.滑块A从右向左运动时，其速度v＝ωs tanα，随角度α变化而不均匀变化，角度α先增大后减小，根据正切 OA 函数的性质可知，滑块先做加速度增大的加速运动，后做加速度减小的减速运动，故A错误； ωRsinβ BC.当O杆OB与AB垂直时，α＝90°﹣β，sinβ＝cosα，则v= =ωR，滑块的速度不是最大，故B，C cosα 错误； D.当β＝90°时，如图所示： 滑块的速度为：ωRsinβ ωR Rω√L2+R2 v= = = cosα L L ，故D正确。 √L2+R2 故选：D。 15. （2022•雨花区校级一模）往复式活塞压缩机简图如图所示，圆盘与活塞通过铰链 A、B连接在轻杆 两端，左侧活塞被轨道固定，只能在AO方向运动。圆盘绕圆心O做角速度为ω的匀速圆周运动。已知OB 距离为r。AB杆长L＞2r，则（ ） A．当杆长不变时，若OB距离变大，活塞运动的范围变小 B．当OB距离不变时，杆长L越大，活塞运动的范围越大 C．当OB垂直于AO时，活塞速度为ωr D．当OB垂直于AB时，活塞速度为ωr 【解答】解：AB、当B点在圆心左侧水平位置时，活塞运动到最左位置，距离O点s ＝L+r，当B点在圆心右 1 侧水平位置时，活塞运动到最右位置，距离O点s ＝L﹣r，所以活塞运动范围为s ﹣s ＝2r，此距离与杆长L无 2 1 2 关，与r成正比，故AB错误； C、圆盘B点速度v ＝rω，当OB垂直于AO时，如下图所示，此时活塞速度方向与圆盘上B点速度方向相同， B 速度方向与杆夹角θ相同，沿杆速度v cosθ＝v cosθ，此时有v ＝v ＝rω，故C正确； B A A B D、当OB垂直于AB时，如下图所示，此时B点的速度方向一定沿杆，则v ≠v ，故D错误。 A B 故选：C。第 9 讲 抛体运动1.掌握平抛运动的特点和性质. 2.掌握研究抛体运动的方法，并能应用解题． 考点一 平抛运动的基本规律 1．性质 加速度为重力加速度g的匀变速曲线运动，运动轨迹是抛物线． 2．基本规律 以抛出点为原点，水平方向(初速度v 方向)为x轴，竖直向下方向为y轴，建立平面直角坐标系，则： 0 (1)水平方向：做匀速直线运动，速度v＝v，位移x＝vt. x 0 0 (2)竖直方向：做自由落体运动，速度v＝gt，位移y＝gt2. y (3)合速度：v＝，方向与水平方向的夹角为θ，则tan θ＝＝. (4)合位移：s＝，方向与水平方向的夹角为α，tan α＝＝. 3．对规律的理解 (1)飞行时间：由t＝ 知，时间取决于下落高度h，与 初速度 v 无关． 0 (2)水平射程：x＝vt＝v，即水平射程由 初速度 v 和 下落高度 h 共同决定，与其他因素无关． 0 0 0 (3)落地速度：v＝＝，以θ表示落地速度与x轴正方向的夹角，有tan θ＝＝，所以落地速度也只与 初速度 v 和下落 t 0 高度 h 有关． (4)速度改变量：因为平抛运动的加速度为重力加速度 g，所以做平抛运动的物体在任意相等时间间隔 Δt内的速度 改变量Δv＝gΔt相同，方向恒为竖直向下，如图所示． (5)两个重要推论 ①做平抛(或类平抛)运动的物体任一时刻的瞬时速度的反向延长线一定通过此时水平位移的中点，如图中 A点和B点所示． ②做平抛(或类平抛)运动的物体在任意时刻任一位置处，设其速度方向与水平方向的夹角为 α，位移方向与水平方 向的夹角为θ，则tan α＝2tan θ. [例题1] （2024•麦积区二模）如图所示，一小球从O点水平抛出后的轨迹途经A、B两点，已知小球经 过A点时的速度大小为 13m/s，从O到A的时间和从A到B的时间都等于0.5s，取重力加速度大小 g＝ 10m/s2，不计空气阻力，下列说法正确的是（ ） A．小球做平抛运动的初速度大小为10m/s B．O、A两点间的距离为5m C．A、B两点间的距离为10m D．O、B两点间的距离为13m 【解析】A.由题意知下落到A点竖直方向的速度为：v ＝gt＝10×0.5m/s＝5m/s，所以小球做平抛运动的初速度 yA 大小为：v =√v2 −v =√132−52m/s=12m/s，故A错误； 0 A yA2 1 1 B.O、A两点间的竖直高度为：y = gt2= ×10×0.52m=1.25m，水平位移为：x ＝v t＝12×0.5m＝6m， A 2 2 A 0 所以O、A两点间的距离为：s =√x2 + y2 =√1.252+62m=6.13m，故B错误； A A A 1 1 D.O、B两点间的竖直高度为：y = g×(2t) 2= ×10×(2×0.5) 2m=5m，水平位移为水平位移为：x ＝ B 2 2 B v ×2t＝12×2×0.5m＝12m，O、B两点间的距离为：s =√x2+ y2=√52+122m=13m，故D正确； 0 B B B C.由上分析知A、B两点间的竖直高度为：h ＝y ﹣y ＝5m﹣1.25m＝3.75m，A、B两点间的水平位移为：x ＝ 1 B A 1 6m，A、B两点间的距离为：s =√ ℎ 2+x2=√3.752+62m=6.32m，故C错误。 1 1 1 故选：D。 [例题2] （多选）（2024•黔南州二模）如图（a）所示，在小球的抛出点O处固定有一点光源，它的正 前方水平距离为L＝1.00m处竖直放置一块毛玻璃屏。用弹射器将小球以某一速度从O点水平向右抛出后，在毛玻璃屏上可以看到小球影子的运动，利用闪光频率为f＝20Hz的频闪相机拍摄了影子的位置照片如图（b） 所示。空气阻力不计，当地的重力加速度g＝9.78m/s2。下列说法正确的是（ ） A．影子做匀速直线运动 B．影子做自由落体运动 C．实验测得小球抛出时的初速度约为6m/s D．实验测得小球抛出时的初速度约为10m/s 【解析】AB．由于相机的曝光时间是一样的，在误差范围内，相邻两个小球的投影间的距离相等，可知小球的 投影是匀速直线运动，故A正确，B错误； 1 1 CD．根据题意可知两相邻投影间的时间间隔为T= = s=0.05s f 20 4.07+4.06+4.08 根据图中数据可知影子的速度大小为v= ×10−2m/s=0.814m/s 3×0.05 1 gt2 由平抛运动的规律可知y 2 = L v t 0 gL 整理得y= t 2v 0 gL 竖直方向投影点做匀速直线运动，则有 =v 2v 0 解得v ≈6m/s 0 故C正确，D错误。 故选AC。 [例题3] （2024•天津模拟）如图所示，正方体框架ABCD﹣A B C D 的底面A B C D 处于水平地面上。 1 1 1 1 1 1 1 1 从顶点A沿不同方向水平抛出小球（可视为质点），不计空气阻力。关于小球的运动，下列说法正确的是（ ）A．落点在棱BB 上的小球，落在B 点时平抛的初速度最大 1 1 B．落点在面A B C D 内的小球，落在C 点的运动时间最长 1 1 1 1 1 C．落点在三角形B C D 内的小球，平抛初速度的最小值与最大值之比是1：2 1 1 1 D．落点在线B D 上的小球，落地时重力的瞬时功率均不相同 1 1 【解析】A、小球做平抛运动，竖直方向做自由落体运动，有h= 1 gt2 得：t= √2ℎ ，则知落点在棱BB 上的小 2 g 1 x 球，水平位移相等，落在B 点时下落高度最大，运动时间最长。根据v = ，可知平抛的初速度最小，故A错 1 0 t 误； √2ℎ B、根据t= 可知落点在面A B C D 内的小球下落高度相等，则运动时间相等，故B错误； 1 1 1 1 g √2 C、落点在三角形B C D 内的小球运动时间相等，最大的水平位移为√2l，最小水平位移为 l，则最小水平 1 1 1 2 x 位移与最大水平位移之比为1：2，由v = ，可知平抛初速度的最小值与最大值之比是1：2，故C正确； 0 t D、设正方体的棱长为l，落点在线B D 上的小球，竖直速度大小均为v =√2gl，落地时重力的瞬时功率P ＝ 1 1 y G mgv 均相同，故D错误。 y 故选：C。 考点二 斜面上的平抛运动问题 斜面上的平抛运动问题是一种常见的题型，在解答这类问题时除要运用平抛运动的位移和速度规律，还要充分运 用斜面倾角，找出斜面倾角同位移和速度与水平方向夹角的关系，从而使问题得到顺利解决．常见的模型如下： 方法 内容 斜面 总结 分 水平：v＝v x 0 分解速度，构建速度 解 竖直：v＝gt y 三角形 速 合速度：v＝度 分 水平：x＝vt 0 解 分解位移，构建位移 竖直：y＝gt2 位 三角形 合位移：s＝ 移 [例题4] （2024•辽宁二模）如图所示，倾角为37°的斜面体固定在水平面上，小球A在斜面底端正上方 以速度v 向右水平抛出，同时，小球B在斜面顶端以速度v 向左水平抛出，两球抛出点在同一水平线上，结 1 2 果两球恰好落在斜面上的同一点，且A球落到斜面上时速度刚好与斜面垂直，不计小球的大小，sin37°＝ 0.6，cos37°＝0.8。则v ：v 等于（ ） 1 2 A．4：3 B．5：4 C．8：7 D．9：8 1 【解析】A、B竖直方向做自由落体运动，位移为ℎ = gt2 2 落点相同即h ＝h ，t ＝t ＝t，v ＝v A B A B A1 B1 1 1 ℎ B = 2 gt2 B = 2 v B1 t，x A ＝v 1 t ℎ tanθ= B x B 3 联立上式代入数据解得tanθ= 2 v 3 垂直打在该点则tanθ= 2 = v 4 A1 v v v 2 4 8 2= A1× 2 = × = v v v 3 3 9 1 1 B1 所以v ：v ＝9：8，故D正确，ABC错误。 1 2 故选：D。 [例题5] （2024•宝鸡一模）如图所示，倾角为θ的斜面上有A、B、C三点，现从这三点分别以不同的初 速度同时水平抛出一小球，不计空气阻力，三个小球均落在斜面上的 D点，测得AB：BC：CD＝5：3：1，由此可判断（ ） A．三个小球做平抛运动的时间之比为1：2：3 B．三个小球落在斜面上时速度方向相同 C．三个小球的初速度大小之比为1：2：3 D．三个小球的运动轨迹可能在空中相交 1 【解析】A．小球做平抛运动，竖直方向有y= gt2 2 根据几何关系有AD：BD：CD＝9：4：1 三个小球做平抛运动的时间之比为t ：t ：t ＝3：2：1 A B C 故A错误； B．小球在水平方向做匀速直线运动，则x＝v t 0 y gt 三个小球均落在斜面上的D点，根据位移间的关系有tanθ= = x 2v 0 v gt 设三个小球速度偏转角为α，则tanα= y = =2tanθ v v 0 0 可知三个小球速度偏转角相同，三个小球落在斜面上时速度方向相同，故B正确； y gt C．三个小球均落在斜面上的D点，根据竖直位移与水平位移的关系有tanθ= = x 2v 0 三个小球的初速度大小之比为v ：v ：v ＝3：2：1 A B C 故C错误； D．三个小球做平抛运动，三个小球的运动轨迹为抛物线，且交于D点，故三个小球的运动轨迹不可能在空中 相交，故D错误。 故选：B。 [例题6] （2024•德州模拟）如图所示，把一小球从斜面上先后以相同大小的速度抛出，一次水平抛出， 另一次抛出的速度方向与斜面垂直，两小球最终都落到斜面上，水平抛出与垂直斜面抛出落点到抛出点的距 离之比为（ ）A．1：2 B．2：1 C．1：1 D．1：3 【解析】设斜面倾角为θ，当小球做平抛运动落在斜面上时； 根据平抛运动规律，水平位移为x＝v t 0 1 竖直位移y= gt2 2 y 根据数学知识tanθ= x x 抛出点与落点之间的距离s = 1 cosθ 2v2tanθ 代入数据解得s = 0 ； 1 gcosθ 当小球垂直于斜面抛出时，小球做斜抛运动，根据运动的合成与分解，竖直分速度 v ＝v cosθ，水平分速度v y 0 x ＝v sinθ 0 以抛出点为参考点，根据斜抛运动规律，水平位移x ＝v t 1 x1 1 竖直位移−y =v t − gt2 1 y 1 2 1 y 根据数学知识tanθ= 1 x 1 x 抛出点与落点之间的距离s = 1 2 cosθ 2v2tanθ 代入数据解得s = 0 ； 2 gcosθ s 1 因此有 1= ，故C正确，ABD错误。 s 1 2 故选：C。考点三 平抛运动的临界问题 [例题7] （2024•重庆模拟）充气弹跳飞人娱乐装置如图1所示，开始时娱乐者静止躺在气包上，工作人 员从站台上蹦到气包上，娱乐者即被弹起并落入厚厚的海洋球。若娱乐者弹起后做抛体运动，其重心运动轨 迹如图2虚线POB所示。开始娱乐者所处的面可视为斜面AC，与水平方向夹角θ＝37°。已知娱乐者从P点 抛起的初速度方向与AC垂直，B点到轨迹最高点O的竖直高度h＝3.2m，水平距离l＝2.4m，AB在同一水平 面上，忽略空气阻力，sin37＝0.6，重力加速度g＝10m/s2，则（ ） A．P点到B点的位移为3.6m B．AB之间的距离为0.4m C．娱乐者从P点到B点过程中的时间为1s D．娱乐者从P点到B点过程中的最大速度9m/s 【解析】由抛体运动的规律可知，从P到B的过程中水平方向的分速度不变，等于在最高点O点的速度，设为 v 0 由平抛运动的规律可得 水平方向l＝v t 01 1 竖直方向h= gt 2 2 1 由已知代入数据解得 t ＝0.8s，v ＝3m/s 1 0 已知在P点速度垂直AC可分解为水平速度v 和竖直向上的分速度v 0 py v v 由几何知识可得；tanθ= 0 tanθ= 0 v v py py v 3 代入数据解得v = 0 = m/s=4m/s py tanθ 0.75从P到O竖直方向做竖直上抛运动，时间t 满足 2 v 4 v ＝gt ，代入数据记得t = py = s=0.4s py 2 2 g 10 1 1 则PO的竖直分位移为y = gt2= ×10×0.42m=0.8m po 2 2 2 水平分位移为x ＝v t ＝3×0.4m＝1.2m po 02 A.PB的水平分位移为x ＝l+x ＝2.4m+1.2m＝3.6m PB po 竖直分位移为y ＝h﹣y ＝3.2m﹣0.8m＝2.4m PB po 由勾股定理可得P到B的位移为L =√x2 + y2 =√3.62+2.42m≈4.089m PB PB PB 故A错误； y 2.4 B.PA的水平分位移为x = PB = m=3.2m PA tanθ 0.75 则AB之间的距离为x ＝x ﹣x ＝3.6m﹣3.2m＝0.4m AB PB PA 故B正确； C.P到B的时间为t＝t +t ＝0.8s+0.4s＝1.2s 1 2 故C错误； D.由抛体运动的规律可知，速度最大的位置为B点，竖直分速度为v ＝gt ＝10×0.8m/s＝8m/s By 1 水平分速度为v ＝3m/s 0 B点速度为v =√82+32m/s=√73m/s，故D错误。 B 故选：B。 [例题8] （2024•重庆一模）如图所示，某同学对着墙壁练习打乒乓球（视为质点），某次乒乓球与墙壁 上的P点碰撞后水平弹离，恰好垂直落在球拍上的Q点，取重力加速度大小g＝10m/s2，不计空气阻力。若球 拍与水平方向的夹角为45°，乒乓球落到球拍前瞬间的速度大小为4m/s，则P、Q两点的高度差为（ ） A．0.1m B．0.2m C．0.4m D．0.8m √2 【解析】由于恰好垂直落在球拍上的Q点，根据几何关系得：v cos45°＝gt，解得t= s Q 5 1 根据乒乓球在竖直方向上的运动规律，由h= gt2， 21 1 2 解得：h= gt2= ×10× m＝0.4m，故C正确，ABD错误。 2 2 25 故选：C。 [例题9] （2024•贵州模拟）无人机在一斜坡上方沿水平方向向右做匀速直线运动，飞行过程中先后释放 甲、乙两个小球，两小球释放的初始位置如图所示。已知两小球均落在斜坡上，不计空气阻力，比较两小球 分别从释放到落在斜坡上的过程，下列说法正确的是（ ） A．乙球的位移大 B．乙球下落的时间长 C．乙球落在斜坡上的速度大 D．乙球落在斜坡上的速度与竖直方向的夹角大 1 【解析】AB．根据位移—时间公式，对于竖直方向做匀加速运动而言ℎ = gt2 ，对于水平方向做匀速运动而 2 言x＝vt √2ℎ 可得t= g 根据题意可知，甲、乙两球均做平抛运动，但由于甲球先释放，乙球后释放，且两球均落在斜坡上，则可知乙 球在斜坡上的落点比甲球在斜坡上的落点高，而平抛运动在竖直方向的分运动为自由落体运动，在水平方向的 运动为匀速直线运动，由于乙球的落点高，则乙球在竖直方向的位移小，由此可知乙球下落的时间小于甲球下 落的时间，即t甲 ＞t乙 乙球在水平方向的位移小于甲球在水平方向的位移，而甲、乙两球的位移s=√ ℎ 2+x2 由于h甲 ＞h乙 ，x甲 ＞x乙 因此可知s甲 ＞s乙 即乙球的位移小于甲球的位移，故AB错误； C．竖直方向的分速度v ＝gt y 由于甲球下落时间大于乙球下落时间，因此小球落在斜坡上时的速度v=√v2+v2 y 由此可知，乙球落在斜坡上的速度小于甲球落在斜坡上时的速度，故C错误； D．设小球落在斜坡上时速度方向与竖直方向的夹角为θ，则小球落在斜坡上时速度与竖直方向夹角的正切值v tanθ= v y 由于v y甲 ＞v y乙 因此tanθ甲 ＜tanθ乙 则有θ甲 ＜θ乙 由此可知，乙球落在斜坡上的速度与竖直方向的夹角大，故D正确。 故选：D。 考点四 类平抛运动模型 1．受力特点 物体所受的合外力为恒力，且与初速度的方向垂直． 2．运动特点 在初速度v 方向上做匀速直线运动，在合外力方向上做初速度为零的匀加速直线运动，加速度a＝. 0 3．求解方法 (1)常规分解法：将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合外力的方向)的匀加 速直线运动．两分运动彼此独立，互不影响，且与合运动具有等时性． (2)特殊分解法：对于有些问题，可以过抛出点建立适当的直角坐标系，将加速度a分解为a、a，初速度v 分解为 x y 0 v、v，然后分别在x、y方向列方程求解． x y [例题10]（2023秋•武昌区校级期末）如图所示的光滑固定斜面ABCD，其倾角可调节。当倾角为θ 时， 1 一物块（可视为质点）沿斜面左上方顶点A以初速度v 水平射入，恰好沿底端D点离开斜面；改变倾角为θ 0 2 时，同样将该物块沿斜面左上方顶点A以初速度v 水平射入，发现物块沿CD边中点离开斜面。已知重力加 0 速度为g，下列说法正确的是（ ） A．物块离开斜面时，前后两次下落的高度之比为2：1 B．物块离开斜面时，前后两次下落的高度之比为4：1 C．物块从入射到飞离斜面，前后两次速度变化量的大小之比为1：1 D．物块从入射到飞离斜面，前后两次速度变化量的大小之比为1：2【解析】AB.第一次，物块恰好沿底端D点离开斜面，第二次，物块沿CD边中点离开斜面，则沿斜面方向的 1 位移y之比2：1，平行斜面方向x相同，根据x＝v t，则时间相同，再根据y= gsinθt2 ，则sinθ ＝2sinθ ，根 0 2 1 2 据结合关系高度h＝ysinθ，故物块离开斜面时，前后两次下落的高度之比为4：1，故A错误，B正确； CD.物块从入射到飞离斜面，前后两次速度变化量Δv＝gsinθt，故前后两次速度变化量的大小之比为2：1，故 CD错误。 故选：B。 [例题11] （多选）（2023秋•包河区校级期末）如图所示，两个倾角分别为30°、45°的光滑斜面放在同一 水平面上，两斜面间距大于小球直径，斜面高度相等。有三个完全相同的小球 a、b、c，开始均静止于同一高 度处，其中b小球在两斜面之间，a、c两小球在斜面顶端。若同时释放a、b、c小球到达该水平面的时间分 别为t 、t 、t若同时沿水平方向抛出，初速度方向如图所示，到达水平面的时间分别为 t ′、t ′、t ′．下列关于 1 2 1 2 3 时间的关系正确的是（ ） A．t ＞t ＞t 1 3 2 B．t ＝t ′、t ＝t ′、t ＝t ′ 1 1 2 2 3 3 C．t ′＞t ′＞t ′ 1 3 2 D．t ＜t ′、t ＜t ′、t ＜t ′ 1 1 2 2 3 3 【解析】第一种情况：b球做自由落体运动，a、c做匀加速运动。设斜面的高度为h，则 对a球： ℎ = 1 gsin30°t2 ， sin30° 2 1 1 对b球：h= gt2 2 2 对c球： ℎ = 1 gsin45°t2 sin45° 2 3 由数学知识得：t ＞t ＞t 。 1 3 2 第二种情况：a、c两个球都做类平抛运动，沿斜面向下方向都做初速度为零的匀加速直线运动，a的加速度为 gsin30°，c的加速度为gsin45°，b球做平抛运动，则有 对a球： ℎ = 1 gsin30°t '2 sin30° 2 1 1 对b球：h= gt '2 2 2对c球： ℎ = 1 gsin45°t '2 sin45° 2 3 比较可知，t ＝t ′、t ＝t ′、t ＝t ′．故ABC正确。D错误 1 1 2 2 3 3 故选：ABC。 [例题12]（多选）如图所示，倾角为θ＝30°的光滑斜面ABCD，其中AB＝BC＝CD＝DA＝2.4m，在斜面 底端A点放置一小球发射装置（可视为质点），发射装置可从A点与AB边成53°沿斜面斜向上射出速度大小 不同的小球，重力加速度g＝10m/s2，sin53°＝0.8，cos53°＝0.6。下列说法正确的是（ ） A．所有小球在斜面上运动过程中，速度的变化率都相等 B．若射出小球的速度为2.5m/s，则小球落到AB边上的位置距离A点0.6m C．若小球恰好能从C点离开斜面，则小球发射的速度为5√2m/s D．若小球垂直于BC边离开斜面，则小球发射的速度为5m/s 【解析】A、所有的小球在斜面上的加速度均为a＝gsinθ＝10×0.5m/s2＝5m/s2，又因为加速度的物理意义是描述 物体速度的变化率，可知所有小球在斜面上运动过程中，速度的变化率都相等，故A正确； B、若射出小球的速度为2.5m/s，小球沿着斜面方向的速度为v ＝vsin53°＝2.5×0.8m/s＝2m/s 1 平行AB方向的速度为v ＝vcos53°＝2.5×0.6m/s＝1.5m/s 2 v 2 小球落到AB边上的位置距离A点x=v ×2× 1=1.5×2× m=1.2m 2 a 5 故B错误； 1 C、若小球恰好能从C点离开斜面，设运动时间为t，设初速度为v′，沿着斜面方向v'sin53°t− at2=AD 2 平行AB方向v′cos53°t＝AB 联立解得v'=5√2m/s 故C正确； D、若小球垂直于BC边离开斜面，设运动时间为t ，设初速度为v''，则有v''sin53°＝at ，v''cos53°＝AB 1 1 联立解得v''＝5m/s 故D正确。 故选：ACD。题型1平抛运动基本规律的应用 1. （2024•甘肃模拟）如图所示，一小球从O点水平抛出后的轨迹途经A，B两点，已知小球经过A点 时的速度大小为13m/s，从O到A的时间和从A到B的时间都等于0.5s，取重力加速度大小g＝10m/s2，不计 空气阻力，下列说法正确的是（ ） A．小球做平抛运动的初速度大小为10m/s B．O、A两点间的距离为5m C．A、B两点间的距离为10m D．O、B两点间的距离为13m 【解析】A。由题意知下落到A点竖直方向的速度为v ＝gt＝10×0.5m/s＝5m/s yA 小球做平抛运动的初速度大小为v =√v2 −v2 0 A yA 解得v ＝12m/s，故A错误； 0 1 1 B、O、A两点间的竖直高度为y = gt2= ×10×0.52m＝1.25m A 2 2 水平位移为x ＝v t＝12×0.5m/s＝6m A 0 所以O、A两点间的距离为s =√x2 + y2 A A A 解得s ＝6.13m，故B错误； A 1 C、O、B两点间的竖直高度为y = g(2t) 2 B 2 解得y ＝5m B 水平位移为x ＝v •2t＝12×2×0.5m＝12m B 0 A、B两点间的竖直高度为h ＝y ﹣y ＝5m﹣1.25m＝3.75m 1 B A A、B两点间的水平位移为x ＝x ﹣x ＝12m﹣6m＝6m 1 B AA、B两点间的距离为s 1 =√x 1 2+ ℎ 1 2 解得s ＝6.32m，故C错误； 1 D、O、B两点间的距离为s =√x2+ y2 B B B 解得s ＝13m，故D正确。 B 故选：D。 2. （2024•富平县一模）高楼出现火情时需要一种高架水炮消防车。现距水平地面 36m高的某楼房出现 火情，消防员紧急出动救援，已知高架水炮消防车的水炮炮口距离水平地面28.8m，到起火房间的水平距离为 9.6m，水柱刚好从起火房间的窗户垂直打入，取重力加速度大小g＝10m/s2，不计空气阻力，则水柱刚打入窗 户时的速度为（ ） A．6m/s B．8m/s C．10m/s D．15m/s 【解析】将水的逆过程看成是平抛运动，竖直方向有 1 Δℎ = gt2 2 √2×(36−28.8) 代入数据可得t= s=1.2s 10 水平方向有 x＝v t 0 解得水平速度为 x 9.6 v = = m/s=8m/s 0 t 1.2 则水柱刚打入窗户时的速度为8m/s，故ACD错误，B正确。 故选：B。 题型2平抛运动的两个重要推论的应用 3. （2024•泸州模拟）将一小球向右水平抛出并开始计时，不计空气阻力。设某时刻小球与抛出点的连 线与水平方向的夹角为α，此时速度的方向与水平方向的夹角为β，下列有关图像中可能正确的是（ ） A． B．C． D． 【解析】根据平抛运动规律，某时刻小球与抛出点的连线与水平方向的夹角为α，则有 y gt tanα= = x 2v 0 v gt 此时速度的方向与水平方向的夹角为β，则有tanβ= y = v v x 0 联立，解得tanβ＝2tanα 可知tanβ与tanα为正比关系。 故选：D。 4. （2021•宁江区校级三模）如图所示，甲、乙两同学模拟古代投壶比赛，他们自P、Q两点分别v 、 1 v 的速度同时水平抛出小球，P比Q位置更高，两小球均射到壶口O点，且在O点时速度方向相同，忽略空 2 气阻力，下列说法正确的是（ ） A．两小球抛出的初速度相等 B．两小球飞行时间相等 C．抛出点P、Q与O共线 D．两小球到达O点的速度相等 【解析】设达到O点时速度方向与水平方向的夹角为α，做平抛运动的初速度为v . 0 gt = AB、在O点时速度方向相同，则速度方向与水平方向夹角相同，tanα ，自P点抛出小球的飞行时间长，因 v 0 此抛出的初速度大，故AB错误； gt D、到达O点的速度v = ，到达O点的速度不等，故D错误； sinα gt 1 C、位移方向与水平方向夹角tanθ = = tanα，因此PQO共线，故C正确。 2v 2 0 故选：C。题型3平抛运动与斜面相结合 5. （2023•大庆模拟）如图所示，光滑斜面AB固定，倾角为37°，斜面上P点与斜面底端B点间的距离 为L，D点位于B点的正上方。现在将小物块从斜面的顶端A点由静止释放的同时，将小球从D点以某一初 速度水平向左抛出，小球与物块在P点相遇，相遇时小球恰好垂直打到斜面上。取 sin37°＝0.6，cos37°＝ 0.8，物块与小球均视为质点，不计空气阻力。A、B两点间的距离为（ ） 28 59 33 107 A． L B． L C． L D． L 25 50 25 75 【解析】（1）小球从D点运动到P点的过程做平抛运动，如图所示： v 有Lcosθ＝v t；tanθ= 0 0 gt √16L 解得：t= 15g 设物块沿斜面下滑的加速度大小为a，根据牛顿第二定律得：mgsinθ＝ma 1 根据运动学公式可得：d= at2 s＝d+L 2 33 解得：s= L 25 故ABD错误，C正确； 故选：C。 6. （2023•郴州模拟）某游乐场有一打金蛋游戏，游戏示意图如下。弹珠的发射速度方向与斜面垂直、 大小可以通过按压的力度来调整，若弹珠弹出后直接击中B点的金蛋为三等奖；若与斜面碰撞一次再击中金 蛋为二等奖；若与斜面碰撞两次再击中金蛋为一等奖，已知斜面与水平方向夹角为45°，斜面AB长√2m，弹 珠与斜面碰撞瞬间弹珠在垂直于斜面方向上的速度反向、大小不变，沿斜面方向上的速度不变，取重力加速度g＝10m/s2，忽略空气阻力影响，以下说法正确的是（ ） A．若最终得到三等奖，则弹珠发射的初速度大小为5m/s B．最终得到一、二、三等奖的弹珠从射出到击中金蛋的时间之比为1：1：1 C．最终得到一、二、三等奖的弹珠从射出到击中金蛋的时间之比为2：3：4 D．最终得到一、二、三等奖的弹珠的初速度之比为4：3：2 【解析】A、将重力加速度g沿斜面方向和垂直于斜面方向分解 沿斜面方向g ＝gsinθ x 垂直于斜面方向g ＝gcosθ y θ＝45° 弹珠沿斜面方向做初速度为0，加速度为g 的匀加速直线运动，在垂直于斜面方向上弹珠做类竖直上抛运动， x 若最終得到三等奖则有 1 x= g t2 2 x 3 2v t = 3 3 g y 解得 弹珠发射的初速度大小v =√5m/s 3 故A错误； BC、从发射出弹珠到击中金蛋，沿斜面方向弹珠一直在做初速度为零，加速度为g 的匀加速直线运动，三种情 x 况的位移一样，所以三种情况运动的时间也相等，即 t ：t ：t ＝1：1：1 1 2 3 故B正确，C错误； D、由速度—时间关系有 6v t = 1 1 g y4v t = 2 2 g y 2v t = 3 3 g y 得最终得到一、二、三等奖的弹珠的初速度之比v ：v ：v ＝2：3：6 1 2 3 故D错误。 故选：B。 题型4平抛运动与圆面相结合 7. （2023•青羊区校级模拟）如图所示，a、b两小球分别从半径大小为R的半圆轨道顶端和斜面顶端以 大小相等的初速度同时水平抛出，已知半圆轨道的半径与斜面竖直高度相等，斜面斜边长是其竖直高度的 2 倍，a、b均可视为质点，结果a、b两球同时分别落在半圆轨道和斜面上，则小球的初速度大小为（ ） （重力加速度为g，不计空气阻力） √3√3gR √3gR A．√2gR B． C．√2√3gR D． 2 2 【解析】a、b两球以相同的初速度同时平抛，同时分别落在半圆轨道和斜面上，可知两小球运动时间相等，在 竖直方向和水平方向的位移大小相等，将右侧三角形斜面放入左侧半圆，三角形斜边与圆弧有一交点，该交点 与抛出点之间竖直方向的距离与水平方向的距离就是小球做平抛运动的竖直位移大小和水平位移大小，分别设 为y和x，并设小球从抛出到落到斜面上所用时间为t，斜面倾角为θ，如图所示。 1 根据题意：斜面斜边长是其竖直高度的2倍，可知：sinθ= 2 则θ＝30° 由几何关系可得1 y=Rsin2θ= gt2 2 x＝R+Rcos2θ＝v t 0 √√3R √3√3gR 联立解得：t= ，v = ，故ACD错误，B正确。 g 0 2 故选：B。 8. （2023•雨花区校级一模）如图示，半圆轨道固定在水平面上，一小球（小球可视为质点）从半圆轨 道上B点沿切线斜向左上方抛出，到达半圆轨道左端 A点正上方某处小球的速度刚好水平，O为半圆轨道圆 心，半圆轨道半径为R，OB与水平方向的夹角为60°，重力加速度为g，不计空气阻力，则小球在A点正上 方的水平速度为（ ） √3√3gR √3gR √√3gR √√3gR A． B． C． D． 2 2 2 3 【解析】小球做斜抛运动，由于到达半圆轨道左端A点正上方某处小球的速度刚好水平，根据逆向思维，可知 小球从一半圆轨道左端A点正上方某处开始做平抛运动，运动过程中恰好与半圆轨道相切于B点，小球运动过 程中恰好与半圆轨道相切于B点，则速度与水平方向的夹角为 30°，设位移与水平方向的夹角为θ，则： y y tan30° √3 tanθ= = √3R √3 tanθ= = ，因为 x 3 ，则竖直位移： y= ，而： v2=2gy= gR，所以： 2 6 R 4 y 2 2 √√3gR v 2 √3√3gR tan30°= y ，解得小球在A点正上方的水平速度为：v = = ，故A正确，BCD错误。 v 0 √3 2 0 3 故选：A。题型5平抛运动与竖直面相结合 9. （2023•湛江二模）如图所示，某同学在篮筐前某位置跳起投篮。篮球出手点离水平地面的高度h＝ 1.8m。篮球离开手的瞬间到篮筐的水平距离为5m，水平分速度大小v＝10m/s，要使篮球到达篮筐时，竖直方 向的分速度刚好为零。将篮球看成质点，篮筐大小忽略不计，忽略空气阻力，取重力加速度大小g＝10m/s2。 篮筐离地面的高度为（ ） A．2.85m B．3.05m C．3.25m D．3.5m 【解析】篮球做斜抛运动，逆过程处理，上升阶段看作平抛运动，水平方向做匀速直线运动，则有：x＝vt，可 x 5 得篮球从抛出运动到篮筐的时间：t= = s=0.5s，篮球到篮筐时竖直方向的速度为零，竖直方向则有： v 10 1 H−ℎ = gt2，代入数据，解得H＝3.05m，故ACD错误，B正确。 2 故选：B。 10. （2023•上饶模拟）如图所示，某同学从O点对准前方的一块竖直放置的挡板将小球水平抛出，O与 A在同一高度，小球的水平初速度分别为v 、v ，不计空气阻力，小球打在挡板上的位置分别是B、C，且 1 2 AB＝BC，则v ：v 为（ ） 1 2 A．2：1 B．√2：1 C．(√2+2)：1 D．(√2+1)：1 1 【解析】小球在空中做平抛运动，由平抛运动规律得，竖直方向：ℎ = gt2 2 水平方向：x＝v t 0 √ g 联立解得：v =x 0 2ℎv √ℎ 所以 1= AC v ℎ 2 AB ℎ 1 又因为 AB = ℎ 2 AC v √2 所以 1= v 1 2 故B正确，ACD错误。 故选：B。 题型6平抛运动在球类问题中的临界问题 11. （2023•东城区模拟）如图所示，窗子上、下沿间的高度H＝1.6m，墙的厚度d＝0.4m，某人在离墙 壁距离L＝1.4m、距窗子上沿h＝0.2m处的P点，将可视为质点的小物件以v的速度水平抛出，小物件直接穿 过窗口并落在水平地面上，取g＝10m/s2。则v的取值范围是（ ） A．v＞7 m/s B．v＜2.3 m/s C．3 m/s＜v＜7 m/s D．2.3 m/s＜v＜3 m/s 【解析】小物件做平抛运动，恰好擦着窗子上沿右侧穿过时v最大， 此时有L＝v t max 1 ℎ = gt2 2 代入数据解得v ＝7m/s max 恰好擦着窗口下沿左侧时速度v最小， 则有L+d＝v t' min 1 H+ ℎ = gt'2 2 代入数据解得v ＝3m/s min 故v的取值范围是3m/s＜v＜7m/s。 故选：C。12. 如图所示，某次排球比赛中，球员A在离水平地面3m的高处将排球以30m/s的速度垂直球网水平击 出，此时排球与球网的水平距离为9m。球网的高度为2m，对方的球员B站立在球网处，直立伸直手臂可拦 到离地高度为2.3m的排球，起跳拦网可拦到离地高度为2.75m的排球，取重力加速度大小g＝10m/s2。已知 球员A、B的连线与球网垂直，不计空气阻力，下列关于球员B拦排球的说法，正确的是（ ） A．排球运动到球网正上方的时间为0.3s B．球员B站在球网前直立伸直手臂可拦到排球 C．若球员B未拦到排球则排球不会出界 D．若球员B未拦到排球，则排球落地点到球网的距离约为2.6m L 9 【解析】A、排球做平抛运动，水平方向为匀速直线运动，则排球运动到球员B位置的时间t = = s=0.3s 1 v 30 故A正确； 1 1 B、排球竖直方向做自由落体运动，该段时间排球下落的高度ℎ = gt 2= ×10×0.32m=0.45m 2 1 2 此时排球离地高度h ＝H﹣h＝3m﹣0.45m＝2.55m＞h ＝2.3m 3 1 故球员B在球网前直立伸直手臂拦不到排球，故B错误； 1 CD、竖直方向，由位移—时间公式得：H= gt 2 2 2 √15 代入数据解得，排球从被击出到落地的时间t = s 2 5 √15 排球运动的水平距离x＝vt ＝30× m＝6√15m＞18m 2 5 排球将出界，故CD错误。 故选：A。 题型7类平抛运动 13. 如图所示的光滑斜面长为l，宽为b，倾角为θ，一物块（可看成质点）沿斜面左上方顶点P以初速度 v 水平射入，恰好从底端Q点离开斜面，则（ ） 0√ 2l A．物块由P点运动到Q点所用的时间t＝2 gsinθ √2l B．物块由P点运动到Q点所用的时间t＝2 g √ g C．初速度v ＝b 0 2l √gsinθ D．初速度v ＝b 0 2l mgsinθ 【解析】AB、根据牛顿第二定律得物体的加速度为：a= =gsinθ。 m 1 √ 2l 根据l = at2得：t= ，故AB错误； 2 gsinθ b √gsinθ CD、入射的初速度为：v = = b ，故C错误，D正确。 0 t 2l 故选：D。 14. 如图所示的光滑斜面长为L，宽为s，倾角为θ＝30°，一小球（可视为质点）沿斜面右上方顶点A处 水平射入，恰好从底端B点离开斜面，重力加速度为g。则下列说法正确的是（ ） A．小球运动的加速度为g √2L B．小球由A运动到B所用的时间为 g √ g C．小球由A点水平射入时初速度v 的大小为s 0 2L √ g D．小球离开B点时速度的大小为 (s2+4L2 ) 4L 【解析】A、依据曲线条件，初速度与合力方向垂直，且合力大小恒定，则物体做匀变速曲线运动， mgsinθ g 再根据牛顿第二定律得，物体的加速度为：a= =gsinθ= ，故A错误； m 21 BCD、根据L= at2，有： 2 √2L √ 2L √4L t= = = a gsinθ g 在B点的平行斜面方向的分速度为： √ 2L v ＝at＝gsinθ× =√2gLsinθ=√gL By gsinθ 根据s＝v t，有： 0 s s = = = √gsinθ √ g v t √ 2L s =s 0 2L 4L gsinθ 故物块离开B点时速度的大小： √ g v=√v2+v2 = (s2+4L2 )，故BC错误；D正确； 0 By 4L 故选：D。 题型8斜抛运动 15. （2024•淮安模拟）将一物体以某一初速度沿与水平方向成 37°角从A点斜向上抛出，经过B点时速 度与水平方向的夹角为53°。已知A、B之间的水平距离为L，忽略空气阻力的影响，重力加速度为g，sin53° ＝0.8，则下列说法正确的是（ ） √3gL A．从A点抛出时的速度大小为 2 3 B．从A到B过程中速度的最小值为 √3gL 5 5√3L C．从A到B的时间为 3 g 7 D．A、B之间的高度差为 L 12【解析】A.设初速度为v，则水平方向的速度为：v ＝vcosθ＝0.8v，竖直方向的速度为：v ＝vsinθ＝0.6v x y 4 16 由于水平方向速度不变，所以末状态下的竖直方向的速度为：v '＝v tan53°＝0.8v• = v y x 3 15 5v 所以取竖直向下为正方向有：﹣v +gt＝v '，解得：t= y y 3g √3gL 水平方向上有L＝v t，解得：v= ，故A正确； x 2 √3gL 2 B.速度最小值是最高点的速度，此时竖直方向速度为零，速度最小，有：v'＝v ＝0.8v＝0.8• = √3gL， x 2 5 故B错误； 5v 5√3l C.从A到B的时间为：t= = ，故C错误； 3g 6 g √3gL 3 D.根据速度关系，竖直方向有：v ＝vsinθ＝0.6v＝0.6• = √3gL y 2 10 1 取竖直向下为正方向有：h＝﹣v t+ gt2 y 2 7 解得：h= L，故D错误； 24 故选：A。 16. （2024•温州二模）如图所示，A、B两位同学从同一高度分别抛出沙包1和2，两沙包抛出的初速度 大小均为v ，方向与水平方向的夹角分别为θ 、θ ，且θ ＞θ ，两沙包抛出后在空中的运动轨迹分别如图中Ⅰ 0 1 2 1 2 和Ⅱ所示。两位同学均能在各自的抛出点接住对方抛来的沙包，不计空气阻力，下列说法正确的是（ ） v2sin2θ A．两抛出点之间的距离为 0 2 g B．沙包1和2在空中运动时间之比为tanθ 2 C．沙包1和2运动过程中最小速度之比为tanθ 1 D．沙包1和2运动过程中离地的最大高度之比为tan2θ 1 【解析】A、沙包做斜抛运动，水平方向做匀速直线运动，竖直方向做竖直上抛运动，故 2v sinθ t= 0 g x＝v cosθt 0v2sin2θ 代入数据解得x= 0 ，故A正确； g B、根据运动的分解 沙包1和2在空中运动的竖直分速度为 v ＝v sinθ y1 0 1 v ＝v sinθ y2 0 2 根据运动学公式又有运动到最高点竖直方向分速度的大小为 v ＝gt y1 1 v ＝gt y2 2 t sinθ 联立整理解得有沙包1和2在空中运动时间之比为： 1= 1 ，故B错误； t sinθ 2 2 C、沙包1和2运动过程中最小速度出现在竖直分速度为零的时刻，故v ＝v cosθ min 0 v cosθ 故沙包1和2运动过程中最小速度之比为 min1= 1 v cosθ min2 2 故C错误； v2sin2θ D、沙包1和2运动过程中离地的最大高度为 ℎ = 0 2g ℎ tan2θ 故沙包1和2运动过程中离地的最大高度之比为： 1= 1 ℎ tan2θ 2 2 故D错误， 故选：A。第 10 讲 圆周运动 1.掌握描述圆周运动的物理量及它们之间的关系 2.理解向心力公式并能应用，圆周运动的动力学分析 3.了解物体做离心运动的条件 考点一 圆周运动中的运动学分析 1．线速度：描述物体圆周运动快慢的物理量．v＝＝. 2．角速度：描述物体绕圆心转动快慢的物理量．ω＝＝. 3．周期和频率：描述物体绕圆心转动快慢的物理量．T＝，T＝. 4．向心加速度：描述速度方向变化快慢的物理量．a＝rω2＝＝ωv＝r. n 5．相互关系：(1)v＝ωr＝r＝ 2π rf . (2)a＝＝rω2＝ωv＝r＝4π2f2r. n[例题1] （2024•齐齐哈尔一模）机动车检测站进行车 辆尾气检测的原理如下：车的主动轮压在两个相同 粗细的有固定转动轴的滚筒上，可使车轮在原地转 动，然后把检测传感器放入尾气出口，操作员将车 轮加速一段时间，在与传感器相连的电脑上显示出 一系列相关参数，现有如下简化图：车内轮A的半 径为r ，车外轮B的半径为 r ，滚筒C的半径为 A B r ，车轮与滚筒间不打滑，当车轮以恒定速度运行 C 时，下列说法正确的是（ ） A．A、B轮的角速度大小之比为r ：r A B B．A、B轮边缘的线速度大小之比为r ：r A B C．B、C的角速度之比为r ：r B C D．B、C轮边缘的向心加速度大小之比为r ：r B C 【解答】解：A、A、B为同轴转动，角速度大小相等，A错误； B、根据v＝ωr可知，A、B轮边缘的线速度大小之比为v ：v ＝r ：r ，B正确； A B A B C、B、C的线速度大小相同，根据v＝ωr可知，B、C的角速度之比为ω ：ω ＝r ：r ，C错误； B C C B v2 D、根据a= 可得B、C轮边缘的向心加速度大小之比为a ：a ＝r ：r ，D错误。 B C C B r 故选：B。 [例题2] （2024•重庆模拟）小明同学站在原地，将圆 形雨伞绕竖直伞柄以角速度ω匀速转动，使附在雨 伞表面的雨滴均沿雨伞边缘的切线方向水平飞出， 最终落至地面成一圆形区域，已知雨伞边缘距地面 的高度为h，到伞柄的垂直距离为R。忽略空气阻力， 以下关于圆形区域半径的表达式正确的是（ ） A．R √2ℎω2 +1 B．ωR √2ℎ +R C．ωR √2ℎ D．R g g g 【解答】解：由题意可知，伞边缘的雨滴做圆周运动的角速度为ω，半径为R，所以雨滴的线速度为 v＝ωR雨滴脱离雨伞后沿伞边缘的切线方向做平抛运动，竖直方向的高度为h，设落地时间为t，则有 1 gt2= ℎ 2 因为在水平方向做匀速直线运动，设水平方向的位移为x，则有x＝vt 雨滴脱离雨伞后，落点形成的圆形区域下图虚线所示： 设落点形成的圆形区域半径为r，根据几何知识有r=√x2+R2 √2ω2 ℎ 代入数据可得：r＝R +1，故BCD错误，A正确。 g 故选：A。 [例题3] （2024•乌鲁木齐模拟）如图所示，轮O 、O 1 3 固定在一转轴上，轮O 、O 用皮带连接且不打滑。 1 2 在O 、O 、O 三个轮的边缘各取一点A、B、C，已 1 2 3 知三个轮的半径比r ：r ：r ＝2：1：1，求： 1 2 3 （1）A、B、C三点的线速度大小之比v ：v ：v 。 A B C （2）A、B、C三点的角速度之比ω ：ω ：ω 。 A B C （3）A、B、C三点的向心加速度大小之比a ：a ：a 。 A B C 【解答】解：（1）A、B两点靠传送带传动，线速度大小相等，A、C共轴转动，角速度相等，根据v＝rω，则 v ：v ＝r ：r ＝2：1。 A C 1 3 所以A、B、C三点的线速度大小之比v ：v ：v ＝2：2：1。 A B C （2）A、C共轴转动，角速度相等，A、B两点靠传送带传动，线速度大小相等，根据v＝rω，ω ：ω ＝r ：r ＝ A B 2 1 1：所以A、B、C三点的角速度之比ω ：ω ：ω ＝1： A B C 2：1。 v2 （3）A、B的线速度相等，根据a= ，知a ：a ＝r ： A B 2 r r ＝1：A、C的角速度相等，根据a＝rω2得，a ：a ＝ 1 A C r ：r ＝2：所以A、B、C三点的向心加速度大小之比 1 3 a ：a ：a ＝2：4：1。 A B C 考点二 圆周运动中的动力学分析 1．向心力的来源 向心力是按力的作用效果命名的，可以是重力、弹力、摩擦力等各种力，也可以是几个力的合力或某个力的分力， 因此在受力分析中要避免再另外添加一个向心力． 2．向心力的确定 (1)确定圆周运动的轨道所在的平面，确定圆心的位置． (2)分析物体的受力情况，找出所有的力沿半径方向指向圆心的合力，就是向心力． 3．向心力的公式 F＝ma ＝m＝ mω 2 r ＝mr＝ mr 4π 2 f 2 n n [例题4] （2024•新郑市校级三模）如图甲所示，一艘 正在进行顺时针急转弯训练的航母，运动轨迹可视 作半径为R的水平圆周。航母在圆周运动中，船身 发生了向外侧倾斜，且甲板法线与竖直方向夹角为 θ，船体后视简图如图乙所示。一质量为m的小物块 放在甲板上，与甲板始终保持相对静止，两者之间 的动摩擦因数为μ（μ＞tanθ）。假设航母的运动半 径R、夹角θ不随航速改变，最大静摩擦力等于滑动 摩擦力。下列说法正确的是（ ）A．航母对小物块的支持力F ＝mgcosθ N B．小物块可能只受重力、支持力两个力作用 C．航母的航速越大，则小物块受到的摩擦力越大 √μ−tanθ D．航母的最大航速v= gR 1+tanθ 【解答】解：AB、根据题意可知，小物块做圆周运动，一定受到重力、支持力、摩擦力，通过正交分解法如图 所示： 由图可知mg﹣f ＝F 2 N2 而F ＝F cosθ N2 N f ＝fsinθ 2 mg−fsinθ 联立解得F = N cosθ 故AB错误； v2 CD、由图可知，小物块做圆周运动的向心力由f 和F 提供，有f −F =m 1 N1 1 N1 R 由于F ＝F sinθ N1 N f ＝fcosθ 1 v2 F sinθ+m 联立上式整理解得 N R f = cosθ 可得航母的航速越大，小物块受到的摩擦力越大； 当最大静摩擦力等于滑动摩擦力时，航母有最大航速，有f＝μF Nv2 代入上式得m =μF cosθ−F sinθ R N N mg−fsinθ mg 由A中得F = = N cosθ μsinθ+cosθ √ μ−tanθ 联立解得v= gR 1+μtanθ 故C正确，D错误。 故选：C。 [例题5] （2024•西城区校级模拟）如图甲、乙所示为 自行车气嘴灯，气嘴灯由接触式开关控制，其结构 如图丙所示，弹簧一端固定在顶部，另一端与小物 块P连接，当车轮转动的角速度达到一定值时，P拉 伸弹簧后使触点A、B接触，从而接通电路使气嘴 灯发光。触点B与车轮圆心距离为R，车轮静止且 气嘴灯在最低点时触点A、B距离为d，已知P与触 点A的总质量为m，弹簧劲度系数为k，重力加速 度大小为g，不计接触式开关中的一切摩擦，小物块 P和触点A、B均视为质点。当该自行车在平直的道 路上行驶时，下列说法中正确的是（ ） √kd+mg A．要使气嘴灯能发光，车轮匀速转动的最小角速度为 mR √kd−mg B．要使气嘴灯能发光，车轮匀速转动的最小角速度为 mR √kd+2mg C．要使气嘴灯一直发光，车轮匀速转动的最小角速度为 mR √kd+mg D．要使气嘴灯一直发光，车轮匀速转动的最小角速度为 mR 【解答】解：AB、当气嘴灯运动到最低点时发光，此时对应车轮做匀速圆周运动的角速度最小，根据受力分析， 向心力由弹簧的弹力与重力的合力提供，又因为初始时弹簧弹力等于重力，所以在最低点是增大的弹力提供向 心力即kd＝mω2R√ kd 得ω= mR 故AB错误； CD、当气嘴灯运动到最高点时能发光，则kd+2mg＝mω′2R √kd+2mg 得ω'= mR √kd+2mg 即要使气嘴灯一直发光，车轮匀速转动的最小角速度为 ，故C正确，D错误。 mR 故选：C。 [例题6] （2023•温州三模）在东北严寒的冬天，有一 项“泼水成冰”的游戏，具体操作是把一杯滚烫的 开水按一定的弧线均匀快速地泼向空中，泼洒出的 小水珠和热气被瞬间凝结成冰而形成壮观的场景。 如图甲所示是某人玩泼水成冰游戏的精彩瞬间，图 乙为其示意图。假设泼水过程中杯子做匀速圆周运 6π 动，在0.4s内杯子旋转了 。下列说法正确的是（ 5 ） A．P位置的小水珠速度方向沿a方向 B．P、Q两位置，杯子的向心加速度相同 C．杯子在旋转时的线速度大小约为6πm/s D．杯子在旋转时的向心加速度大小约为9π2m/s2 【解答】解：A、由图乙中做离心运动的轨迹可知，杯子的旋转方向为逆时针方向，P位置飞出的小水珠初速度 沿b方向，故A错误； B、向心加速度是矢量，P、Q两位置，杯子的向心加速度方向不同，故向心加速度不相同，故B错误； Δθ C、杯子旋转的角速度为：ω= ，代入数据得：ω＝3πrad/s，杯子做圆周运动的半径约为1m，杯子在旋转时 Δt 的线速度大小约为：v＝ωR＝3π×1m/s＝3πm/s，故C错误；D、杯子旋转的轨迹半径约为1m，则向心加速度大小约为：a＝ω2R＝9π2×1m/s2＝9π2m/s2，故D正确。 故选：D。 考点三 圆周运动的临界问题 1．有些题目中有“刚好”、“恰好”、“正好”等字眼，明显表明题述的过程中存在着临界点． 2．若题目中有“取值范围”、“多长时间”、“多大距离”等词语，表明题述的过程中存在着“起止点”，而这 些起止点往往就是临界点． 3．若题目中有“最大”、“最小”、“至多”、“至少”等字眼，表明题述的过程中存在着极值，这些极值点也 往往是临界点． [例题7] （多选）（2024•南明区校级一模）如图所示， 质量均为m的甲、乙、丙三个小物块（均可看作质 点）水平转盘一起以角速度ω绕OO′轴做匀速圆周 运动，物块甲叠放在物块乙的上面，所有接触面间 的动摩擦因数均为μ。已知甲、乙到转轴的距离为 r ，丙到转轴的距离为r ，且r ＞r 。最大静摩擦力 1 2 2 1 等于滑动摩擦力，重力加速度为g。下列说法正确的 是（ ） A．甲受到的摩擦力一定为μmg B．乙受到转盘的摩擦力一定为2mω2r 1 C．若角速度增大，丙先达到滑动的临界点 D．若角速度增大，甲先达到滑动的临界点 【解答】解：A、对甲进行受力分析，水平方向上，摩擦力提供向心力，则f =mω2r ，由于不是滑动摩擦力， 甲 1 不能用μmg来判断摩擦力的大小，故A错误； B、对甲和乙整体分析，水平方向上，静摩擦力提供向心力，则f =(m+m)ω2r =2mω2r ，故B正确； 乙 1 1CD、因为三个物块转动的角速度一样，且动摩擦因数也一样，但物块丙做圆周运动的半径更大，所以若角速度 增大的话，丙先达到滑动的临界点，故C正确，D错误。 故选：BC。 [例题8] （2023•山东模拟）如图所示，水平机械臂 BC固定在竖直转轴CD上，B处固定一与BC垂直 的光滑水平转轴，轻杆AB套在转轴上。轻杆可在 竖直面内转动，其下端固定质量为m的小球，轻杆 和机械臂的长度均为L，开始小球静止，缓慢增大 竖直轴转动的角速度，直至杆与竖直方向的夹角为 37°，已知sin37°＝0.6，cos37°＝0.8，重力加速度为 g，则（ ） √5g A．此时小球的角速度大小为 4L √3gL B．此时小球的线速度大小为 2 4 C．此过程中杆对小球做的功为 mgL 5 3 D．此过程中杆对小球做的功为 mgL 5 【解答】解：AB、当杆与竖直方向成37°时，小球做匀速圆周运动，杆对小球的拉力沿杆方向，合力提供向心 力，则有：F合 ＝mgtan37°＝ma 3 可得：a=gtan37°= g 4 8 由几何关系可知，圆周运动半径：r=L+Lsin37°= L 5 v2 根据向心加速度的公式：a=rω2= r √15g √6gL 联立以上可得：ω= ，v= ，故AB错误； 32L 5 1 CD、设此过程中杆对小球做功为W，由动能定理：W−mgL(1−cos37°)= mv2 24 解得：W = mgL，故C正确，D错误。 5 故选：C。 [例题9] （多选）（2023•河南模拟）一个可以转动的 玩具装置如图所示，四根轻杆OA、OC、AB和CB 与两小球及一小环通过铰链连接，轻杆长均为L， 球和环的质量均为m，O端固定在竖直的轻质转轴 上。套在转轴上的轻质弹簧连接在O与小环之间， 3 原长为L。装置静止时，弹簧长为 L。如果转动该 2 装置并缓慢增大转速，发现小环缓慢上升。弹簧始 终在弹性限度内，忽略一切摩擦和空气阻力，重力 加速度为g。则下列说法正确的是（ ） 4mg A．弹簧的劲度系数k= L 2mg B．弹簧的劲度系数为k= L √8g C．装置转动的角速度为 时，AB杆中弹力为零 5L √6g D．装置转动的角速度为 时，AB杆中弹力为零 5L 【解答】解：AB、装置静止时，小球受力平衡，设OA、AB杆中的弹力分别为F 、T ，OA杆与转轴的夹角为 1 1 θ ，由平衡条件得： 1 竖直方向：F cosθ +T cosθ ＝mg 1 1 1 1 水平方向：F sinθ ＝T sinθ 1 1 1 1 0.75L 根据几何关系得：cosθ = 1 L 2 联立解得：T = mg 1 33 小环受力平衡，对小环由平衡条件得：F弹1 ＝k（ 2 L﹣L）＝mg+2T 1 cosθ 1 4mg 解得：k= L 故A正确，B错误； CD、AB杆中弹力为零时，设OA杆中的弹力为F ，OA杆与转轴的夹角为θ ，弹簧长度为x，小环受力平衡， 2 2 由平衡条件得：F弹2 ＝k（x﹣L）＝mg 对小球受力分析，竖直方向，由平衡条件得：F cosθ ＝mg 2 2 水平方向，由牛顿第二定律得：F sinθ =mω2Lsinθ 2 2 0 2 x 由几何关系得：cosθ = 2 2L √8g 联立解得：ω = 0 5L 故C正确，D错误。 故选：AC。 考点四 竖直平面内圆周运动绳、杆模型 1．在竖直平面内做圆周运动的物体，按运动到轨道最高点时的受力情况可分为两类：一是无支撑(如球与绳连接、 沿内轨道运动的过山车等)，称为“绳(环)约束模型”，二是有支撑(如球与杆连接、在弯管内的运动等)，称为“杆 (管)约束模型”． 2．绳、杆模型涉及的临界问题 绳模型 杆模型 常见类型 均是没有支撑的小球 均是有支撑的小球 过最高点的 由mg＝m得 由小球恰能做圆周运动得v ＝0 临 临界条件 v ＝ 临 (1)当v＝0时，F ＝mg，F 为支持力，沿 N N (1)过最高点时，v≥，F ＋mg N 半径背离圆心 ＝m，绳、圆轨道对球产生弹 (2)当0时，F ＋mg＝m，F 指向圆心并 N N 圆轨道 随v的增大而增大[例题10] （2024•石景山区一模）如图所示，轻杆的一 端固定在通过O点的水平转轴上，另一端固定一小 球，轻杆绕O点在竖直平面内沿顺时针方向做匀速 圆周运动，其中A点为最高点、C点为最低点，B 点与O点等高，下列说法正确的是（ ） A．小球经过A点时，所受杆的作用力一定竖直向下 B．小球经过B点时，所受杆的作用力沿着BO方向 C．从A点到C点的过程，杆对小球的作用力不做功 D．从A点到C点的过程，小球重力的功率先增大后减小 【解答】解：A、小球经过A点时，由合外力提供向心力，当小球速度较大时 mv2 若 ＞mg，则小球所受杆的作用力竖直向下； r mv2 当小球速度较小时，若 ＜mg，则小球所受杆的作用力竖直向上； r mv2 当小球速度满足 =mg r 则杆对小球无作用力，故A错误； B、小球经过B点时，由合外力提供向心力，小球受重力和杆给的作用力，则小球所受杆的作用力为右上方， 杆的作用力一定不会沿着BO方向，故B错误； C、从A到C的过程中，重力做正功，根据动能定理得W G +W杆 ＝ΔE k ＝0，则W杆 ＝﹣W G ，故杆对小球的作用 力做负功，故C错误； D、A点和C点处重力与速度方向垂直，则小球重力的功率为0，B点处重力与速度共线，故重力功率不为0， 则从A点到C点的过程，小球重力的功率先增大再减小，故D正确。 故选：D。 [例题11] （多选）（2024•绵阳模拟）如图甲所示，质量为0.2kg的小球套在竖直固定的光滑圆环上，并在 圆环最高点保持静止。受到轻微扰动后，小球由静 止开始沿着圆环运动，一段时间后，小球与圆心的 连线转过θ角度时，小球的速度大小为v，v2与cosθ 的关系如乙图所示，g取10m/s2。则（ ） A．圆环半径为0.6m π B．θ= 时，小球所受合力为4N 2 C．0≤θ≤π过程中，圆环对小球的作用力一直增大 D．0≤θ≤π过程中，圆环对小球的作用力先减小后增大 1 【解答】解：A、小球下滑过程由机械能守恒定律有mg(R−Rcosθ)= mv2 2 π 当θ= 时，小球的速度平方为12m2/s2，代入公式得R＝0.6m，故A正确； 2 π mv2 0.2×12 B、当θ= 时，小球的速度平方为12m2/s2，此时是圆环对小球的弹力提供向心力，有N= = N＝ 2 R 0.6 4N 小球还受竖直向下的重力，所以小球所受合力为F=√N2+(mg) 2=√42+(0.2×10) 2N=2√5N，故B错误； π v2 CD、当0＜θ＜ 时，有mgcosθ−N=m 2 R 可知随θ的增大，同时v也增大，所以N必须减小， π v2 当 ＜θ＜π时，有N−mgcos(180°−θ)=m 2 R 可知随θ的增大，同时v也增大，所以N必须增大，所以0≤θ≤π过程中，圆环对小球的作用力先减小后增大， 故C错误，D正确。 故选：AD。 [例题12] （2024•雨花区校级模拟）如图所示，半径R ＝1m的光滑圆环形滑杆MNP竖直固定放置，左侧 端点M和圆心O 的连线与竖直方向夹角的余弦值 1cosθ＝0.15，右侧端点P和圆心O 、O 在同一水平 1 2 线上，P点的切线沿竖直方向。现有一质量 m ＝ 1 0.2kg的小橡胶环A以v ＝1.2m/s的初速度水平抛出， 0 恰好沿滑杆左侧端点M的切线套入滑杆，在滑杆的 最高点静止着质量m ＝0.2kg的小橡胶环B。在右侧 2 端点 P 的正下方 h＝4.15m 处，有一质量 m ＝ 3 0.1kg、长度L＝3m的长直木杆C竖直静止在水平面 上，但跟水平面并不黏合。已知小橡胶环 B与长直 木杆C之间的滑动摩擦力大小f＝2N，最大静摩擦 力大小等于滑动摩擦力，小橡胶环A、B均可视为 质点，两小橡胶环之间和小橡胶环与水平面间的碰 撞都是弹性碰撞；小橡胶环B套入长直木杆C后， 长直木杆C不倾倒，且每次与水平面碰撞瞬间都会 立即停下而不反弹、不倾倒。不计空气阻力，取g＝ 10m/s2。 （1）小橡胶环A到达滑杆最低点Q时所受弹力大小； （2）小橡胶环B在长直木杆C上上滑的最大距离； （3）长直木杆C跟水平面第一次碰撞瞬间损失的机械能； （4）小橡胶环B在长直木杆C上运动的总路程。 【解答】解：（1）小橡胶环A恰好沿滑杆左侧端点M的切线套入滑杆，设小橡胶环A在M点时的速度为 v ， M 则根据速度的合成可得：v cosθ＝v M 0 代入数据解得：v ＝8m/s M 1 1 小橡胶环A从M点到Q点，根据动能定理：m gR(1−cosθ)= m v2 − m v2 1 2 1 Q 2 1 M 代入数据解得：v ＝9m/s Qv2 小橡胶环A在Q点时，支持力和重力的合力提供向心力：N−m g=m Q 1 1 R 代入数据解得：N＝18.2N （2）设小橡胶环 A 从 Q 点运动到最高点与小橡胶环 B 碰撞前的速度为 v ，根据动能定理： A 1 1 −m g×2R= m v2 − m v2 1 2 1 A 2 1 Q 设小橡胶环A和小橡胶环B碰后的速度分别为v ′和v ，根据动量守恒， A B 以向右为正有：m v ＝m v ′+m v 1 A 1 A 2 B 1 1 1 由机械能守恒可得： m v2 = m v'2 + m v2 2 1 A 2 1 A 2 2 B 小 橡 胶 环 B ， 从 碰 撞 后 到 与 长 直 木 杆 接 触 前 瞬 间 ， 设 接 触 前 速 度 为 v ， 根 据 动 能 定 理 ： 1 1 m g(R+ ℎ)= m v2− m v2 2 2 2 2 2 B 代入数据联立解得：v＝12m/s 小橡胶环B沿长直木杆下滑时，长直木杆静止不动，根据受力分析可得：m g＝f 2 可得小橡胶环B在长直木杆C上受力平衡做匀速直线运动，小橡胶环B做匀速直线运动；小橡胶环B沿长直木 杆上滑时，小橡胶环B做匀减速直线运动，长直木杆C做匀加速直线运动，设共速时速度大小为v ，对小橡胶 1 环B有：m g+f＝m a 2 2 1 根据速度—时间公式：v ＝v﹣a t 1 11 对长直木杆有：f﹣m g＝m a 3 3 2 同理有：v ＝a t 1 21 v 位移：x = 2t 1 2 1 v+v v 此时小橡胶环B上滑的距离最大：s = 1t − 1t 1 2 1 2 1 v2 122 代入数据得：s = = m＝2.4m 1 6a 6×10 2 （3）小橡胶环B与长直木杆C共速后一起做竖直上抛，直到长直木杆跟水平面第一次碰撞前， 则由速度—位移公式有：v'2−v2=2gx 1 1 1 解得长直木杆跟水平面第一次碰撞瞬间前的速度大小为：v ′=4√2m/s 1 1 长直木杆跟水平面第一次碰撞瞬间损失的机械能为：ΔE= m v'2 2 3 1 代入数据得：ΔE＝1.6J（4）长直木杆跟水平面第一次碰撞后，小橡胶环先沿长直木杆做匀速下滑，小橡胶环跟水平面碰撞后小橡胶环 沿长直木杆上滑时，小橡胶环做匀减速直线运动，长直木杆做匀加速直线运动，第二次共速后又一起做竖直上 抛，直到长直木杆跟水平面第二次碰撞，由运动学可列， 对橡胶环B：v ＝v ′﹣a t 2 1 12 v 对长杆：v ＝a t ，v'2−v2=2g× 2t 2 22 2 2 2 2 √2 √2 联立可得长直木杆跟水平面第二次将要碰撞时的速度大小为：v ′=√2v = v '=( ) 2v 2 2 3 1 3 √2 √2 所以可得长直木杆跟水平面第n次将要碰撞时的速度大小表达式为：v ′=( ) nv=12×( ) n n 3 3 小橡胶环沿长直木杆第一次下滑的路程为L，小橡胶环跟水平面碰撞后小橡胶环沿长直木杆，在长直木杆上第 v+v v 一次上滑的路程为：s = 1t − 1t 1 2 1 2 1 v2 122 代入数据得：s = = m＝2.4m 1 6a 6×10 2 长直木杆跟水平面第一次碰撞后，小橡胶环先沿长直木杆在长直木杆上做匀速下滑的路程为 s ，小橡胶环跟水 1 v '+v v 平面碰撞后小橡胶环沿长直木杆上滑时，在长直木杆上第二次上滑的路程为：s = 1 2t − 2t 2 2 1 2 1 2 代入数据得：s = s 2 9 1 长直木杆跟水平面第一次碰撞后，小橡胶环先沿长直木杆在长直木杆上做匀速下滑的路程为 s ，以此类推小橡 2 胶环在长直木杆上运动的总路程：s＝L+2s +2s +2s +…… 1 2 3 2s 2×2.4 + 1 = + 321 代入数据得：s＝L 2 3m 2 m= m 1− 1− 35 9 9 题型1圆周运动基本物理量的关系 1. （2023•漳州模拟）如图为明代出版的《天工开物》 中记录的“牛转翻车”，该设备利用畜力转动不同 半径齿轮来改变水车的转速，从而将水运送到高处。图中a、b分别为两个齿轮边缘上的点，齿轮半径之 比为r ：r ＝4：3；a、c在同一齿轮上且a、c到转 a b 轴的距离之比为r ：r ＝2：1，则在齿轮转动过程中 a c （ ） A．a、b的角速度相等 B．b的线速度比c的线速度小 C．b、c的周期之比为3：4 D．a、b的向心加速度大小之比为4：3 【解答】解：A、由图可知a、b为同缘传动时，边缘点的线速度大小相等，故 v ＝v ，由于半径不同，根据公 a b 式v＝ωr，可知a、b的角速度不相等，故A错误； B、a与c同轴传动，角速度相等，即ω ＝ω ，因a、c到转轴的距离之比为r ：r ＝2：1，由公式v＝ωr，可得： a c a c v ＝2v ，又v ＝v ，则v ＝2v ，故B错误； a c a b b c 2π T ω ω r 3 C、由公式T= ，可得b、c的周期之比为： b= c = a= b= ，故C正确； ω T ω ω r 4 c b b a v2 a r 3 D、由公式a= ，可得a、b的向心加速度之比为： a= b= ，故D错误。 r a r 4 b a 故选：C。 2. （2023•绵阳模拟）如图，带车牌自动识别系统的直 杆道闸，离地面高为1m的细直杆可绕O在竖直面 内匀速转动。汽车从自动识别线ab处到达直杆处的 时间为2.3s，自动识别系统的反应时间为0.3s；汽车 可看成高1.6m的长方体，其左侧面底边在aa′直线上， 且O到汽车左侧面的距离为0.6m，要使汽车安全通 过道闸，直杆转动的角速度至少为（ ）π 3π π π A． rad/s B． rad/s C． rad/s D． rad/s 6 8 8 12 【解答】解：设汽车恰好能通过道闸时直杆转过的角度为θ， 1.6−1 由几何知识得：tanθ= =1， 0.6 π 解得：θ= ， 4 直杆转动的时间：t＝t汽车 ﹣t反应时间 ＝（2.3﹣0.3）s＝2s π π 直杆转动的角速度至少为：ω θ 4 rad/s= rad/s，故ABD错误，C正确。 = = 8 t 2 故选：C。 题型2三种传动方式及特点 3. （2023•台州二模）某款机械表中有两个相互咬合的 齿轮A、B，如图所示，齿轮 A、B的齿数之比为 1：2，齿轮匀速转动时，则A、B齿轮的（ ） A．周期之比T ：T ＝2：1 1 2 B．角速度之比为ω ：ω ＝2：1 1 2 C．边缘各点的线速度大小之比v ：v ＝1：2 1 2 D．转速之比为n ：n ＝1：2 1 2 【解答】解：C、齿轮A、B的齿数之比为1：2，可知齿轮A、B的半径之比为1：2；齿轮A、B相互咬合，可知边缘各点的线速度大小相等，即v ：v ＝1：1，故C错误； 1 2 B、根据v＝ωr可得齿轮A、B角速度之比为ω ：ω ＝r ：r ＝2：1，故B正确； 1 2 2 1 2π A、根据T= 可得齿轮A、B周期之比为T ：T ＝ω ：ω ＝1：2，故A错误； ω 1 2 2 1 D、根据ω＝2πn可得齿轮A、B转速之比为n ：n ＝ω ：ω ＝2：1，故C错误； 1 2 1 2 故选：B。 4. （2023•崇明区二模）如图为车库出入口采用的曲杆 道闸，道闸由转动杆OP与横杆PQ链接而成，P、Q 为横杆的两个端点。在道闸抬起过程中，杆PQ始终 保持水平，则在抬起过程中P和Q两点（ ） A．线速度相同，角速度相同 B．线速度相同，角速度不同 C．线速度不同，角速度相同 D．线速度不同，角速度不同 【解答】解：由于在P点绕O点做圆周运动的过程中，杆PQ始终保持水平，即PQ两点始终相对静止，所以两 点的线速度相同，角速度也相同，故A正确，BCD错误； 故选：A。 5. （多选）（2024•鹿城区校级模拟）如图甲所示，光 电编码器由码盘和光电检测装置组成，电动机转动 时，码盘与电动机旋转轴同速旋转，发光二极管发 出的光经凸透镜转化为平行光，若通过码盘镂空的 明道照在光敏管上，信号端输出高电位，反之输出 低电位，两个光敏管分布在同一半径上。根据输出 两路信号可以测量电动机的转速和判断旋转方向。 从左往右看，内、外都均匀分布20个明道的码盘如 图乙所示，电动机转动时两信号的图像如图丙所示， 则（ ）A．从左往右看，电动机顺时针转动 B．从左往右看，电动机逆时针转动 C．电动机转动的转速为50r/s D．电动机转动的转速为125r/s 【解答】解：AB．由图丙可知，在t＝1×10﹣3s时，信号A开始输出低电位，此时信号B开始输出高电位，结 合图乙可知，从左往右看，电动机顺时针转动，故A正确，B错误； CD．由图丙可知，电动机转动的周期为T＝20×1×10﹣3s＝2×10﹣2s 2π 2π 则角速度为ω= = rad/s=100πrad/s T 2×10−2 根据ω＝2πn ω 100π 可得电动机转动的转速为n= = r/s=50r/s 2π 2π 故C正确，D错误。 故选：AC。 题型3锥摆模型 6. （多选）（2024•东莞市一模）如图（a）为游乐场 中的“空中飞椅”项目。“空中飞椅”结构示意图 如图（b），转动轴带动顶部圆盘转动，悬绳一端系 在圆盘边缘，另一端系着椅子。若所有椅子质量相 等，悬绳长短不一定相等，忽略悬绳质量与空气阻 力，则坐在椅子上的游客与椅子整体随圆盘匀速转 动的过程中（ ）A．任一时刻，所有游客的线速度都相同 B．所有游客做圆周运动的周期都相同 C．悬绳越长，悬绳与竖直方向的夹角就越大 D．悬绳与竖直方向的夹角与游客质量无关 【解答】解：AB．由图可知所有游客为同轴转动，则所有游客做圆周运动的角速度相同，游客做圆周运动的半 2π 径不同，由v＝ωr可知，线速度大小不同，游客的线速度方向也不同；由T= 可知，所有游客做圆周运动的 ω 周期都相同，故A错误，B正确； CD．根据题意，绳长L越长，若悬绳与竖直方向的夹角θ不变，则圆周运动半径增大，所需向心力增大，游客 做离心运动，θ变大。 根据：mgtanθ＝mω2（Lsinθ+R盘 ） 可知，悬绳与竖直方向的夹角与游客质量无关，故CD正确。 故选：BCD。 7. （2023•龙华区校级四模）如图所示，小球甲在竖直 面内摆动的周期为T ，悬线长为L；小球乙在水平 0 面内做匀速圆周运动，悬点为 O 、轨迹圆圆心为 1 O ，甲、乙两小球都能视为质点。下列说法正确的 2 是（ ） A．小球甲的向心力由合力来充当 B．小球乙的向心力由拉力来充当 C．若小球乙运动的周期为T ，则与小球乙连接的悬线长度为L 0 D．若O 、O 两点间的距离为L，则小球乙运动的周期为T 1 2 0 【解答】解：A、对甲球受力分析，甲球的向心力是由细线的拉力和重力沿细线方向的分力的合力提供，故A错误； B、小球乙在水平面内做匀速圆周运动，乙球的向心力是拉力沿水平方向的分力提供，故B错误； CD、对乙球进行受力分析，设悬线与竖直方向的夹角为α，O 、O 两点间的距离为h，轨迹圆半径为r， 1 2 根据牛顿第二定律得 4π2 mgtanα=m r， T2 又由几何关系得tanα= r ，解得T=2π √ℎ ℎ g √L 对比甲球的摆动周期T =2π 可知，当T＝T 时，解得h＝L，则知小球乙连接的悬线长度为大于L，O 、O 0 g 0 1 2 两点间的距离为L，故C错误，D正确。 故选：D。 8. （2023•江苏一模）如图所示，一轻支架由水平段 ON和竖直段OO'组成。轻弹簧一端固定于O点，另 一端与套在水平杆ON上的A球相连，一根长为L ＝10cm 的轻绳连接 A、B 两球。A 球质量 m ＝ A 1kg，B球质量m ＝4kg，A球与水平杆的动摩擦因 B 数 μ＝0.36，弹簧原长 l＝20cm，劲度系数 k＝ 450N/m。初始时使A球尽量压缩弹簧并恰好处于静 止状态。现使系统绕OO'轴缓慢转动起来，转动过 程中保持A、B两球始终与OO'在同一竖直平面内。 当系统以某角速度稳定转动时，细绳与竖直方向成 37°角，此时弹簧的弹力大小恰好与初始时相同。设 最大静摩擦力等于滑动摩擦力，不计空气阻力。 sin37°＝0.6，cos37°＝0.8，g＝10m/s2，求： （1）初始时弹簧的长度； （2）细绳与竖直方向成37°角时，系统转动的角速度； （3）整个过程中驱动力对系统所做的总功。【解答】解：已知l＝20cm＝0.2m，L＝10cm＝0.1m （1）初始时，弹簧处于压缩状态，A球恰好处于静止状态，设初始时弹簧的压缩量为Δl，由平衡条件有 kΔl＝μ（m +m ）g A B 解得：Δl＝0.04m 则初始时弹簧的长度为l ＝l﹣Δl＝0.2m﹣0.04m＝0.16m 0 （2）当系统以某角速度稳定转动，弹簧的弹力大小与初始时相同时，弹簧处于拉伸状态，且伸长量与初始状态 的压缩量相等。 对B球，由牛顿第二定律有 m gtan37°＝m ω2r B B B 其中r ＝l+Δl+Lsin37°＝0.2m+0.04m+0.1×0.6m＝0.3m B 解得：ω＝5rad/s （3）根据能量守恒知，整个过程中驱动力对系统所做的功等于 A、B球的动能增加、B球的重力势能增加、A 球与水平横杆间摩擦产生的内能之和，则有 1 1 W= m [(l+Δl)ω] 2+ m (ωr ) 2+m gL（1﹣cos37°）+μ（m +m ）g•2Δl 2 A 2 B B B A B 解得：W＝7.46J 题型4转弯模型 9. （2023•昆明一模）图甲是市区中心的环岛路，A、B 两车正在绕环岛做速度大小相等的匀速圆周运动， 如图乙所示。下列说法正确的是（ ） A．A、B两车的向心加速度大小相等 B．A车的角速度比B车的角速度大C．A、B两车所受的合力大小一定相等 D．A车所受的合力大小一定比B车的大 v2 【解答】解：ACD、两车的线速度v大小相等，由图可知r ＞r ，由a = 可得A车的向心加速度大于B车向 B A n r 心加速度，匀速圆周运动合力全部提供向心力，两车的质量关系未知，由F＝ma 可知，两车的向心力即合力大 n 小无法确定，故ACD错误； v B、由ω= 可知，A车的角速度大于B车角速度，故B正确。 r 故选：B。 1 10. （2024•济南模拟）如图所示，MN为半径为r的 4 圆弧路线，NP为长度13.5r的直线路线，MN'为半 1 径为4r的 圆弧路线，N'P'为长度10.5r的直线路线。 4 赛车从M点以最大安全速度通过圆弧路段后立即以 最大加速度沿直线加速至最大速度v 并保持v 匀速 m m 行驶。已知赛车匀速转弯时径向最大静摩擦力和加 速时的最大合外力均为车重的n倍，最大速度v ＝5 m √ngr，g为重力加速度，赛车从M点按照MNP路 线到P点与按照MN'P'路线运动到P'点的时间差为（ ） π 13 √ r π 3 √ r A．( − ) B．( − ) 2 10 ng 2 2 ng 23 √ r π √ r C．(π− ) D．( +4−2√7) 10 ng 2 ng1 mv2 【解答】解：赛车在半径为r的 圆弧匀速转弯时，由牛顿第二定律有：nmg= 1，可得v =√ngr 4 r 1 1 s 2πr πr 赛车在 圆弧运动的时间：t = ，其中s= = 4 1 v 4 2 1 π √ r 代入数据可得：t = 1 2 ng 赛车在 NP 段从 v 加速到 v 过程，由牛顿第二定律有：nmg＝ma，可得 a＝ng，这一过程需要的时间： 1 m v −v t = m 1 2 a √ r 代入数据可得：t =4 2 ng v +v 赛车在NP段加速过程运动的位移：x= 1 mt 2 2 代入数据可得：x＝12r 13.5r−x x＜13.5r，赛车到达最大速度后，匀速运动，匀速运动的时间：t = 3 v m 3 √ r 代入数据可得：t = 3 10 ng 1 mv2 赛车在半径为4r的 圆弧匀速转弯时，由牛顿第二定律有：nmg= 2，可得v =2√ngr 4 4r 2 1 s' 2π×4r 赛车在半径为4r的 圆弧运动的时间：t '= ，其中s'= =2πr 4 1 v 4 2 √ r 代入数据可得：t '=π 1 ng v −v 赛车在N′P′段从v 加速到v 过程，加速度大小与在NP段加速度大小相等，这一过程需要的时间：t '= m 2 2 m 2 a √ r 代入数据可得：t '=3 2 ng v +v 赛车在N′P′段加速过程运动的位移：x'= 2 mt ' 2 2 代入数据可得：x′＝10.5r，可知赛车到达P′点时，恰好到达最大速度v m 赛车从M点按照MNP路线到P点与按照MN'P'路线运动到P'点的时间差Δt＝t ′+t ′﹣（t +t +t ） 1 2 1 2 3 π 13 √ r 代入数据可得：Δt=( − ) ，故A正确，BCD错误。 2 10 ng 故选：A。 11. （2024•成都模拟）图甲是正在水平面内工作的送餐机器人，该机器人沿图乙中ABCD曲线给16号桌送 餐，已知弧长和半径均为4m的圆弧BC与直线路径 AB、CD相切，AB段长度也为4m，CD段长度为 12m，机器人从A点由静止匀加速出发，到B点时 速率恰好为 1m/s，接着以 1m/s 的速率匀速通过 BC，通过C点后以1m/s的速率匀速运动到某位置后 开始做匀减速直线运动，最终停在16号桌旁的D点。 已知餐盘与托盘间的动摩擦因数μ＝0.1，关于该运 动的说法正确的是（ ） A．B到C过程中机器人的向心加速度a＝0.2m/s2 B．餐盘和水平托盘不发生相对滑动的情况下，机器人从C点到D点的最短时间t＝12.5s C．A到B过程中餐盘和水平托盘会发生相对滑动 D．若重新设置机器人，使其在BC段以3m/s匀速率通过，餐盘与水平托盘间不会发生相对滑动 v2 12 【解答】解：A.从B运动到C的过程中机器人的向心加速度为：a= = m/s2=0.25m/s2，故A错误； r 4 μmg B.机器人以1m/s的初速度匀减速至D点的最大加速度为：a = =μg=0.1×10m/s2=1m/s2 m m v 1 最短的减速时间为：t = = s=1s 1 a 1 m v2 12 匀减速过程的最小位移为：Δx= = m=0.5m 2a 2×1 m x −Δx 12−0.5 从C点开始匀速运动的时间为：t = CD = s=11.5s 2 v 1 从C运动到D点的最短时间为：t＝t +t ＝1s+11.5s＝12.5s，故B正确； 1 2 v2 12 C.对由A到B的过程有：a= = m/s2=0.125m/s2＜a =1m/s2，即加速度小于发生相对滑动的临 2x 2×4 m 界加速度1m/s2，故A到B过程中餐盘和水平托盘不会发生相对滑动，故C错误；D.在BC段餐盘与托盘恰好不发生相对滑动时，由最大静摩擦力提供向心力，则有： v2 μmg=m m，解得：v m ＝2m/s＜3m/s，则餐盘与水平托盘间会发生相对滑动，故D错误。 R 故选：B。 题型5圆盘模型 12. （多选）（2023•上饶模拟）如图所示，A、B为钉 在光滑水平面上的两根细铁钉，将可视为质点的小 球C用长为L 的轻绳拴在铁钉B上，轻绳能承受足 0 够大的拉力，t＝0时刻，A、B、C在同一直线上， 给小球C一个垂直于轻绳的速度，使小球绕着两根 铁钉在水平面上做圆周运动，每次轻绳碰到铁钉时 小球的速度大小不变。在第5s末时轻绳第一次碰到 铁钉A，轻绳的拉力由4N突变为5N，小球碰到铁 钉时立即停止运动，下列说法正确的是（ ） 2 A．A、B间的距离为 L 5 0 1 B．A、B间的距离为 L 5 0 C．在t＝13s时轻绳第二次碰到铁钉 D．在t＝9s时轻绳第二次碰到铁钉 mv2 【解答】解：AB．碰到铁钉A前，轻绳的拉力为4N，绳子的拉力提供向心力，根据牛顿第二定律有F = 1 L 0 mv2 碰到铁钉A后，轻绳的拉力为5N，根据牛顿第二定律有F = 2 L −x 0 AB 1 解得A、B间的距离x = L ，故A错误，B正确； AB 5 0 CD．小球第一次碰到铁钉前的转动半径与第二次碰到铁钉前的转动半径之比为5：4，所以圆的周长之比变为5：4，所以时间之比为5：4，所以小球再经过4s第二次碰到铁钉时间，即小球在t＝9s时轻绳第二次碰到铁钉， 故C错误，D正确。 故选：BD。 13. （多选）（2023•郴州模拟）如图所示。在匀速转动 的水平圆盘上，沿直径方向放着用轻绳相连的物体 A和B，A和B质量都为m。它们分居圆心两侧， 与圆心的距离分别为R ＝r，R ＝3r，A、B与盘间 A B 的动摩擦因数相同且均为μ。若最大静摩擦力等于滑 动摩擦力，当圆盘转速从零开始逐渐加快到两物体 刚好要发生但还未发生滑动时，下列说法正确的是 （ ） A．绳子的最大张力为F ＝2μmg T √2μg B．当A所受的摩擦力为零时，圆盘的角速度为ω= r C．随着角速度的增大，A所受摩擦力的方向和大小都会变化，而B所受的摩擦力方向不变 D．随着角速度的增大，A所受的摩擦力一直减小，而B所受的摩擦力一直增大 【解答】解：A、A和B质量都为m，因B物体离中心轴更远，由F ＝mω2r知B物体所需要的向心力较大，两 n 个物体与圆盘间的最大静摩擦力相等，所以当转速增大时，B先有滑动的趋势，此时B所受的静摩擦力沿半径 指向圆心，A所受的静摩擦力沿半径背离圆心，当B刚要发生相对滑动时，以B为研究对象，由牛顿第二定律 有 T+μmg＝mω 2•3r m 以A为研究对象，由牛顿第二定律有 T﹣μmg＝mω 2r m √μg 联立解得：T＝2μmg，ω = ，故A正确； m r B、当A所受的摩擦力为零时，以B为研究对象，有 T′+μmg＝mω 2•3r 2 以A为研究对象，有T′＝mω 2r 2 √μg 联立解得：ω = ，故B错误； 2 2rCD、刚开始角速度较小时，A、B两个物体由所受的静摩擦力提供向心力，因 B物体离中心轴更远，故B物体 √μg 所需要向心力更大，即B物体所受到的静摩擦力先达到最大值，此时则有μmg＝mω 2•3r，解得ω = ，故当 1 1 3r √μg 0＜ω≤ 时，A、B两物体所受的静摩擦力都增大，此时A、B所受摩擦力方向都指向圆心； 3r √μg √μg 当 ＜ω≤ 时，A物体所受静摩擦力的大小减小，方向指向圆心，B物体所受静摩擦力达到最大，大小 3r 2r √μg √μg 不变，方向指向圆心；当 ＜ω≤ 时，A物体所受的静摩擦的大小增大，方向背离圆心，B物体所受静 2r r 摩擦力达到最大，大小不变，方向指向圆心，故C正确，D错误。 故选：AC。 14. （2023•丰台区一模）如图所示，一圆盘在水平面内 绕过圆盘中心的轴匀速转动，角速度是 2.0rad/s。盘 面上距圆盘中心10cm的位置有一个质量为0.1kg的 小物体随圆盘一起做匀速圆周运动。小物体与圆盘 之间的动摩擦因数μ＝0.4，两者之间的最大静摩擦 力等于滑动摩擦力，重力加速度g取10m/s2。求： （1）小物体随圆盘匀速转动时所需向心力的大小F； （2）要使小物体在圆盘上不发生相对滑动，圆盘角速度的最大值ω ； m （3）若圆盘由静止开始转动，逐渐增大圆盘的角速度，小物体从圆盘的边缘飞出，经过0.4s落地，落地点距飞 出点在地面投影点的距离为40cm。在此过程中，摩擦力对小物体所做的功W。 【解答】解：（1）由题意，小物体随圆盘做匀速圆周运动，半径为r＝10×10﹣2m，根据向心力公式 F＝mω2r 代入数据解得小物体随圆盘匀速转动时所需向心力的大小为F＝0.04N （2）由题意知，当小物体受到的最大静摩擦力等于向心力时，将发生相对滑动，此时对应圆盘的角速度最大， 由牛顿第二定律和向心力公式有μmg=mω2 r m 代入数据解得ω =2√10rad/s m x （3）小物体飞出后做平抛运动，其水平位移x＝40×10﹣2m，设其运动时间为t，由平抛运动规律有v= t 代入数据解得v＝1m/s 小物体由静止到飞出的过程中，由动能定理有 1 W = mv2−0 2 代入数据解得W＝0.05J 题型6离心现象的应用与防止 15. （2023•浙江模拟）高速离心机用于快速沉淀或分离 物质。如图所示，水平试管固定在高速离心机上， 离心机的转速为n，在水平试管中有质量为m的某 固体颗粒，某时刻颗粒离转轴的距离为r。已知试管 中充满液体，颗粒与试管内壁不接触。下列说法正 确的是（ ） 2π A．颗粒运动的角速度为 n B．颗粒此时受到的合外力大小必为4π2mrn2 C．离转轴越远，分离沉淀效果越好 D．此款高速离心沉淀机，适用于任何颗粒，颗粒都会到试管底部沉淀 【解答】解：A、根据角速度与转速的关系，可得颗粒运动的角速度为ω＝2πn，故A错误； B、如果颗粒在此处做匀速圆周运动，合外力必为 F＝4π2mrn2，但从题义上不能得出它在此稳定做圆周运动， 故B错误；C、离转轴越远，r越大，需要的向心力越大，就越易做离心运动，也就越容易分离，故C正确； D、只能将密度比液体密度大的颗粒沉在的底部，故D错误。 故选：C。 16. （2023•东莞市校级模拟）如图为自行车气嘴灯及其 结构图，弹簧一端固定在A端，另一端拴接重物， 当车轮高速旋转时，LED灯就会发光。下列说法正 确的是（ ） A．安装时A端比B端更远离圆心 B．高速旋转时，重物由于受到离心力的作用拉伸弹簧从而使触点接触，电路导通，LED灯发光 C．增大重物质量可使LED灯在较低转速下也能发光 D．匀速行驶时，若LED灯转到最低点时能发光，则在最高点时也一定能发光 【解答】解：A、要使重物做离心运动，M、N接触，则A端应靠近圆心，因此安装时A端比B端更远离气嘴， 故A错误； B、转速越大，所需向心力越大，弹簧拉伸的越长，M、N接触时灯就会发光，不能说重物受到离心力作用，故 B错误； C、灯在最低点时，F弹 ﹣mg＝mω2r √F g 解得：ω= 弹− ，因此增大重物的质量可使LED灯在较低转速下也能发光，故C正确； mr r mv2 D、灯在最低点时，F ﹣mg= 1 r mv'2 灯在最高点时，F +mg= 2 r 匀速行驶时，在最低点时弹簧对重物的弹力大于在最高点时对重物的弹力，因此匀速行驶时，若 LED灯转到最 低点时能发光，则在最高点时不一定能发光，故D错误； 故选：C。