文档内容
2025
内部
新高考数学
圆锥曲线黄金55题
精研好题,跳出题海
适合110分以上圆锥曲线黄金55题
【建议110分以上使用】
单选题(共10小题)
x2 y2
1 已知双曲线C: - =1(a>0,b>0)的左、右焦点分别为F,F,M,N为双曲线一条渐
a2 b2 1 2
2π
近线上的两点,A为双曲线的右顶点,若四边形MFNF 为矩形,且∠MAN= ,则双曲线C的
1 2 3
离心率为 ( )
21
A. 3 B. 7 C. D. 13
3
圆锥曲线黄金55题 12 已知F为抛物线y2=2px的焦点,过F的直线l与抛物线交于A,B两点,以AF、BF为直径
的圆分别与x轴交于异于F的M,N两点,且MF=2FN,则直线l的斜率为 ( )
1 1
A. B. 2 2 C. ± D. ±2 2
3 3
2 公众号:邦达数学3 已知直线l:2kx-2y-kp=0与抛物线C:y2=2px(p>0)相交于A,B两点,点M(-1,-1)
是抛物线C的准线与以AB为直径的圆的公共点,则下列结论错误的是 ( )
A. p=2 B. k=-2
C. △MAB的面积为5 5 D. |AB|=5
圆锥曲线黄金55题 34 已知抛物线y2=2x的焦点为F,准线为l,圆C经过点F并与抛物线相交于点M,若|MF|=
5
,且圆C与l相切,则这样的圆一共有( )个.
2
A. 1 B. 2 C. 3 D. 4
4 公众号:邦达数学5 已知抛物线y2=2px(p>0)的焦点为F,过点F的直线l交抛物线于A,B两点,若|AF|,
|AB|
,|FB|成等比数列,则线段AB在y轴上的射影长为 ( )
4
A. p B. 2p C. 3p D. 4p
圆锥曲线黄金55题 5x2 y2
6 已知F、F 分别是双曲线C: - =1(a>0,b>0)的左、右焦点,过点F 向一条渐近线
1 2 a2 b2 1
作垂线,交双曲线右支于点P,直线FP与y轴交于点Q(P,Q在轴同侧),连接QF,若△PQF 的
2 1 1
内切圆圆心恰好落在以FF 为直径的圆上,则双曲线的离心率为 ( )
1 2
A. 3 B. 2 C. 5 D. 2
6 公众号:邦达数学x2 y2
7 已知椭圆C: + =1的左、右顶点分别为A,B,F为椭圆C的右焦点,圆x2+y2=9上
9 8
有一动点P,P不同于A,B两点,直线PA与椭圆C交于点Q,k ,k 分别为直线BP,QF的斜
1 2
k
率则 1 的取值范围是 ( )
k
2
9
A. -∞,
8
圆锥曲线黄金55题 7
B. (-∞,-1)∪(-1,0)
3
C. -∞,
4
3
D. (-∞,0)∪0,
4
1 1
8 关于曲线M:x2 +y2 =1,有下述两个结论:①曲线M上的点到坐标原点的距离最小值是
2 1
;②曲线M与坐标轴围成的图形的面积不大于 ,则下列说法正确的是 ( )
2 2
A. ①、②都正确 B. ①正确②错误 C. ①错误②正确 D. ①、②都错误
8 公众号:邦达数学x2 y2
9 已知圆C :x2+y2=b2和椭圆C : + =1(a>b>0).直线y=kx与圆C 交于A、A
1 2 a2 b2 1 1
|OB|
两点,与椭圆C 交于B、B 两点.若k∈R时, 的取值范围是(1,2],则椭圆C 的离心率
2 1 |OA| 2
为 ( )
1 2 3 3
A. B. C. D.
2 2 2 4
圆锥曲线黄金55题 9x2 y2
10 设椭圆C: + =1(a>b>0)的左,右顶点为A,B.P是椭圆上不同于A,B的一点,
a2 b2
a 2
设直线AP,BP的斜率分别为m,n,则当 3-
b 3mn
10 公众号:邦达数学
2
+ +3(ln|m|+ln|n|)取得最小值
mn
时,椭圆C的离心率为 ( )
1 2 4 3
A. B. C. D.
5 2 5 2多选题(共15小题)
11 已知抛物线C:y2=2px,C的准线与x轴交于K,过焦点F的直线l与C交于A,B两点,连
接AK、BK,设AB的中点为P,过P作AB的垂线交x轴于Q,下列结论正确的是 ( )
A. |AF|•|BK|=|AK|•|BF| B. tan∠AKF=cos∠PQF
p2
C. △AKB的面积最小值为 D. |AB|=2|FQ|
2
圆锥曲线黄金55题 1112 设F为抛物线C:y2=2px(p>0)的焦点,过点F的直线l与抛物线C交于A(x ,y )B(x ,
1 1 2
y )两点,过B作与x轴平行的直线,和过点F且与AB垂直的直线交于点N,AN与x轴交于点
2
M,则 ( )
A. xx +yy 为定值
1 2 1 2
B. 当直线l的斜率为1时,△OAB的面积为 2P(其中O为坐标原点)
C. 若Q为C的准线上任意一点,则直线QA,QF,QB的斜率成等差数列
p
D. 点M到直线FN的距离为
2
12 公众号:邦达数学x2 y2
13 已知曲线C: - =1(m≠0) ( )
4 m
A. 若曲线C表示椭圆,则m<0且m≠-4
B. 若m=5时,以P(1,1)为中点的弦AB所在的直线方程为5x-4y-1=0
C. 当m<-4时,F,F 为曲线C的焦点,P为曲线C上一点,且PF ⊥PF,则△PFF 的面积等
1 2 1 2 1 2
于4
1 1 4
D. 若m>0时,直线l过曲线C的焦点F且与曲线相交于A,B两点,则 + =
|AF| |BF| m
圆锥曲线黄金55题 13x2 y2
14 已知曲线C: + =1,F,F 分别为C的左、右焦点,点P在C上,且△PFF 是直角
m m-6 1 2 1 2
三角形,下列判断正确的是 ( )
A. 曲线C的焦距为2 6
B. 若满足条件的点P有且只有4个,则m的取值范围是m>6且m≠12
C. 若满足条件的点P有且只有6个,则m=12
D. 若满足条件的点P有且只有8个,则m的取值范围是0b>0)中,其所有外切矩形的顶点在一个定圆Γ:x2+y2=a2+
a2 b2
b2上,称此圆为该椭圆的蒙日圆.该圆由法国数学家G•Monge(1746-1818)最先发现.若椭圆
x2 y2
C: + =1,则下列说法正确的有 ( )
16 9
A. 椭圆C外切矩形面积的最小值为48
B. 椭圆C外切矩形面积的最大值为48
C. 点P(x,y)为蒙日圆Γ上任意一点,点M(-10,0),N(0,10),当∠PMN取最大值时,
tan∠PMN=2+ 3
D. 若椭圆C的左、右焦点分别为F,F,过椭圆C上一点P和原点作直线l与蒙日圆相交于点
1 2
M,N,则PF•PF =PM•PN
1 2
圆锥曲线黄金55题 153
16 已知抛物线C:y2=2px(p>0)的焦点为F,其准线与x轴交于点M- ,0
2
16 公众号:邦达数学
,过点F作不
垂直于x轴的直线l与C交于A,B两点.设P为x轴上一动点,Q为AB的中点,且AB⊥PQ,
则 ( )
27
A. 抛物线C的方程为y2=3x B. |AB|+3|BF|的最小值为
2
C. |AB|>2|PF| D. |BF|(|MA|+|MB|)=2|MB||PF|17 已知抛物线C:y2=2px(p>0)的焦点为F(1,0),坐标原点为O,直线l与抛物线C交于A,
B两点(与O均不重合),以线段AB为直径的圆过原点O,则△AOB与△AOF的面积之和能为
( )
A. 17 B. 8 5 C. 18 D. 9 3
圆锥曲线黄金55题 1718 过抛物线C:y2=2px(p>0)焦点F的直线与C交于A,B两点,点A,B在C的准线l上的
射影分别为A,B,O为坐标原点,则 ( )
1 1
A. 以AB为直径的圆与准线l相切
B. △OAF可能为正三角形
1 1 2
C. + =
|AF| |BF| p
D. 记△AAF,△AFB,△FBB的面积分别为S,S ,S ,则S2=4SS
1 1 1 1 1 2 3 2 1 3
18 公众号:邦达数学y2
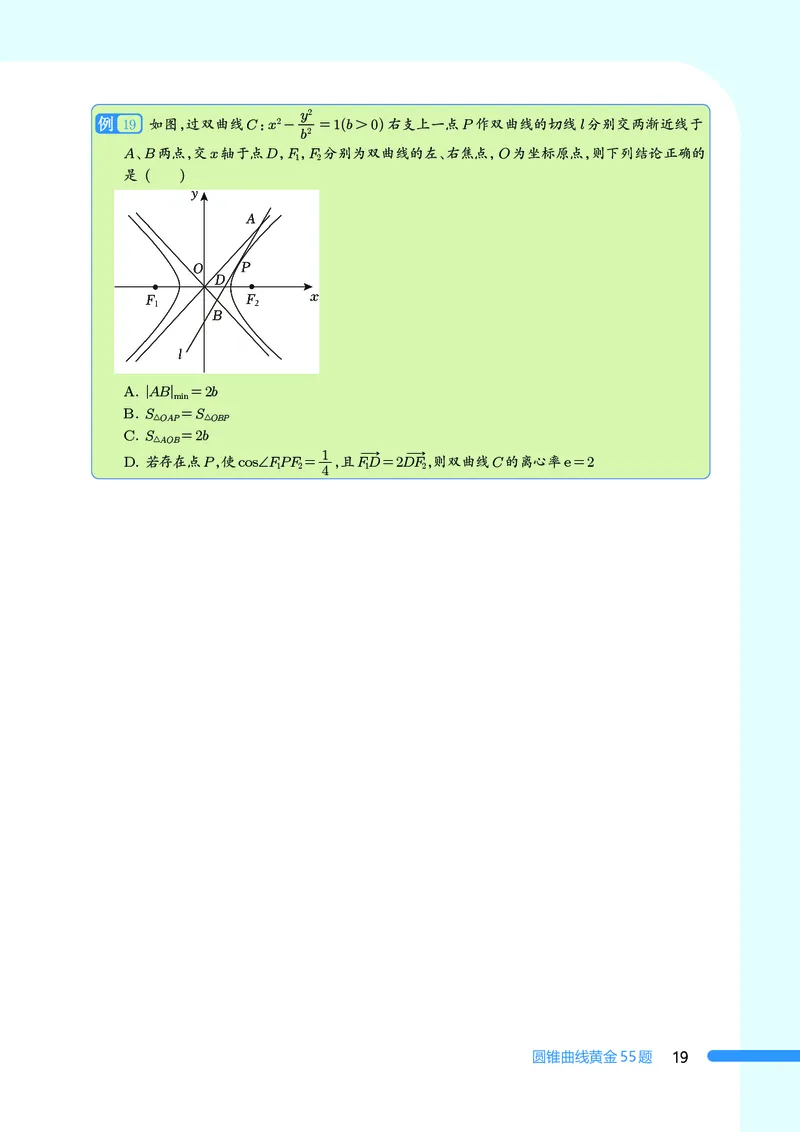
19 如图,过双曲线C:x2- =1(b>0)右支上一点P作双曲线的切线l分别交两渐近线于
b2
A、B两点,交x轴于点D,F,F 分别为双曲线的左、右焦点,O为坐标原点,则下列结论正确的
1 2
是 ( )
A. |AB| =2b
min
B. S =S
△OAP △OBP
C. S =2b
△AOB
1
D. 若存在点P,使cos∠FPF = ,且FD=2DF,则双曲线C的离心率e=2
1 2 4 1 2
圆锥曲线黄金55题 19x2 y2
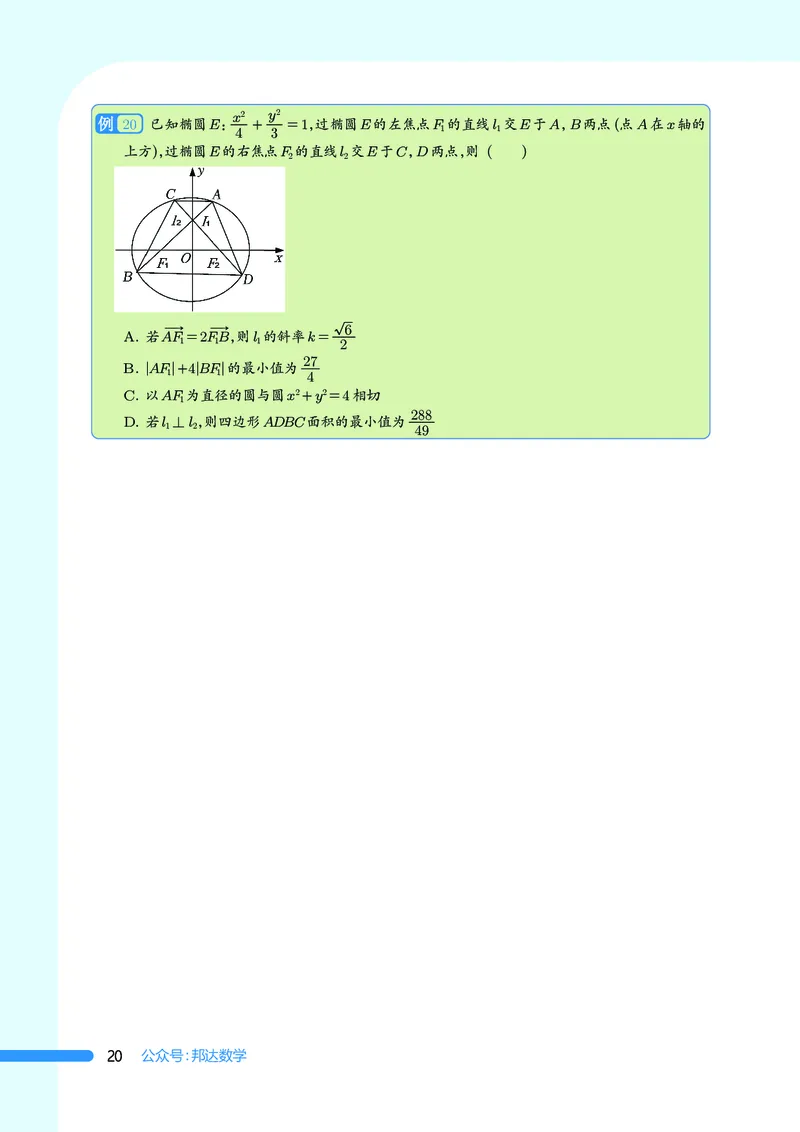
20 已知椭圆E: + =1,过椭圆E的左焦点F 的直线l 交E于A,B两点(点A在x轴的
4 3 1 1
上方),过椭圆E的右焦点F 的直线l 交E于C,D两点,则 ( )
2 2
6
A. 若AF =2FB,则l 的斜率k=
1 1 1 2
27
B. |AF|+4|BF|的最小值为
1 1 4
C. 以AF 为直径的圆与圆x2+y2=4相切
1
288
D. 若l ⊥l ,则四边形ADBC面积的最小值为
1 2 49
20 公众号:邦达数学21 已知抛物线C:y2=2px(p>0)的焦点F与圆E:x2+y2-2x=0的圆心重合,直线l与C交
于A(x ,y )、B(x ,y )两点,且满足OA⋅OB=0(其中O为坐标原点且A,B均不与O重合),则
1 1 2 2
( )
A. xx =16,yy =-16 B. 直线l恒过定点(4,0)
1 2 1 2
C. A,B中点轨迹方程:y2=2x-4 D. △AOB面积的最小值为16
圆锥曲线黄金55题 21x2 y2
22 已知双曲线Γ: - =1(a>0,b>0),左焦点为F,左右顶点分别为A 、A ,B(0,b),P
a2 b2 1 2
是Γ右支上一动点,且|PF|+|PB|的最小值为( 3+2)a,P关于x轴的对称点为Q,则下列结论
正确的是 ( )
A. Γ的离心率为2 B. PA ⊥AQ
2 1
C. sin∠QPA =sin∠QA A D. 4|PB|≥ 6|PQ|
1 2 1
22 公众号:邦达数学x2 y2
23 已知椭圆C: + =1的左右焦点为F,F,若P为椭圆C上一动点,记△PFF 的内心
4 3 1 2 1 2
为I,外心为M,重心为G,且△PFF 内切圆I的半径为r,△PFF 外接圆M的半径为R,则
1 2 1 2
( )
π
A. ∠FPF 的最大值为 B. r的最大值为 3
1 2 3
R
C. PI⋅PG为定值 D. 的最小值为2
r
圆锥曲线黄金55题 23x2 y2 15 1
24 已知F,F 是双曲线C: - =1(a>0,b>0)的左、右焦点,A ,
1 2 a2 b2 2 2
24 公众号:邦达数学
是C上一
2 3
点,若C的离心率为 ,连结AF 交C于点B,则 ( )
3 2
x2
A. C的方程为 -y2=1 B. ∠FAF =90°
3 1 2
C. △FAF 的周长为2 5+2 D. △ABF 的内切圆半径为 5- 3
1 2 125 抛物线C:y2=6x,AB是C的焦点弦 ( )
A. 点P在C的准线上,则PA⋅PB的最小值为0
B. 以AB为直径的所有圆中,圆面积的最小值为9π
C. 若AB的斜率k= 3,则△ABO的面积S=12
9
D. 存在一个半径为 的定圆与以AB为直径的圆都内切
4
圆锥曲线黄金55题 25填空题(共10小题)
x2 y2
26 已知椭圆C: + =1(a>b>0),O(0,0),P(3,1)斜率为-1的直线与C相交于A,B
a2 b2
两点,若直线OP平分线段AB,则C的离心率等于 .
26 公众号:邦达数学x2 y2
27 设F,F 是椭圆E: + =1(a>b>0)的左、右焦点,过点F 且斜率为 3的直线交椭
1 2 a2 b2 1
圆于点P,若∠PFF =2∠PFF,则椭圆E的离心率为 .
1 2 2 1
圆锥曲线黄金55题 2728 已知动抛物线y=x2+ax+b(其中a∈R,b≤0)与动直线y=t(t≥1)交于A、B两点且与
动直线y=t+1交于C、D两点,ABCD构成一个梯形,S为这个梯形的面积,AD为其一腰长,
1
则 S2+16AD2的最小值为 .
4
28 公众号:邦达数学x2 y2
29 椭圆E: + =1,其左焦点是F,过F的直线与椭圆交于A,B两点(不同于长轴的端
4 3
点),已知点P(-4,0),则:
①直线PA与直线PB的斜率的和为0;
|PA|
②△PAF与△PBF的面积之比为 ;
|PB|
1
③点A到直线x=-4的距离等于 |AF|;
2
9
④S ≤ .
△ABP 2
以上说法中正确的是 .(写出所有正确命题的序号)
圆锥曲线黄金55题 2930 已知P为抛物线y2=4x上任意一点,则点P到y轴的距离与点P到直线l:12x-5y+13=
0的距离之和的最小值为 .
30 公众号:邦达数学31 某同学在篮球场打球时,无意间发现当球放在地面上时,球的斜上方的一颗灯泡照过来的光
线使得球在地面上留下了影子,这个影子有点像数学课堂上学过的椭圆,但自己还是不太确定这
个想法,于是他回到家里重新翻阅了教材对椭圆这一节知识进行学习和思考,当他读到教材中的
阅读材料后瞬间明白自己的猜想是没有问题的,而且通过学习,他还确定地面和球的接触点(切
点)就是椭圆影子的焦点,如图,地平面上有一个球,其中球的半径为1个单位长度,在球的右上
方有一个灯泡(当成质点),灯泡与地面的距离为3个单位长度,灯泡垂直照射在平面的点为A,
椭圆的顶点中到A点的距离最短时为1个单位长度,则这个椭圆的离心率 .
圆锥曲线黄金55题 31x2
32 已知椭圆 +y2=1的左右焦点分别为F,F,过F 的直线AB与椭圆交于AB两点,则
2 1 2 2
△FAB的周长是 ,△FAB内切圆面积的最大值是 .
1 1
32 公众号:邦达数学33 已知抛物线C:x2=4y的焦点为F,直线l:x=5,点A,B分别是抛物线C、直线l上的动点,
若点B在某个位置时,仅存在唯一的点A使得|AF|=|AB|,则满足条件的所有|AB|的值为
.
圆锥曲线黄金55题 33x2
34 已知过椭圆E: +y2=1的左焦点F的直线l交E于A,B两点,则|AF|+2|BF|的最小值
2
为 .
34 公众号:邦达数学n
35 已知一族双曲线E :x2-y2= (n∈N*,且n≤2020),设直线x=2与E 在第一象限内
n 2020 n
的交点为A ,点A 在E ,的两条渐近线上的射影分别为B ,∁ ,记△A B ∁ 的面积为a ,则a +
n n n n n n n n n 1
a +a +⋯⋯+a = .
2 3 2020
圆锥曲线黄金55题 35解答题(共20小题)
x2 y2
36 已知双曲线 - =1(a>b>0)左、右焦点为F,F,其中焦距为2 7,双曲线经过点D
a2 b2 1 2
(4,3).
(1)求双曲线的方程;
(2)过右焦点F 作直线交双曲线于M,N两点(M,N均在双曲线的右支上),过原点O作射线OP,
2
其中OP⊥MN,垂足为E,P为射线OP与双曲线右支的交点,求4|MN|-|OP|2的最大值.
36 公众号:邦达数学x2 y2 3
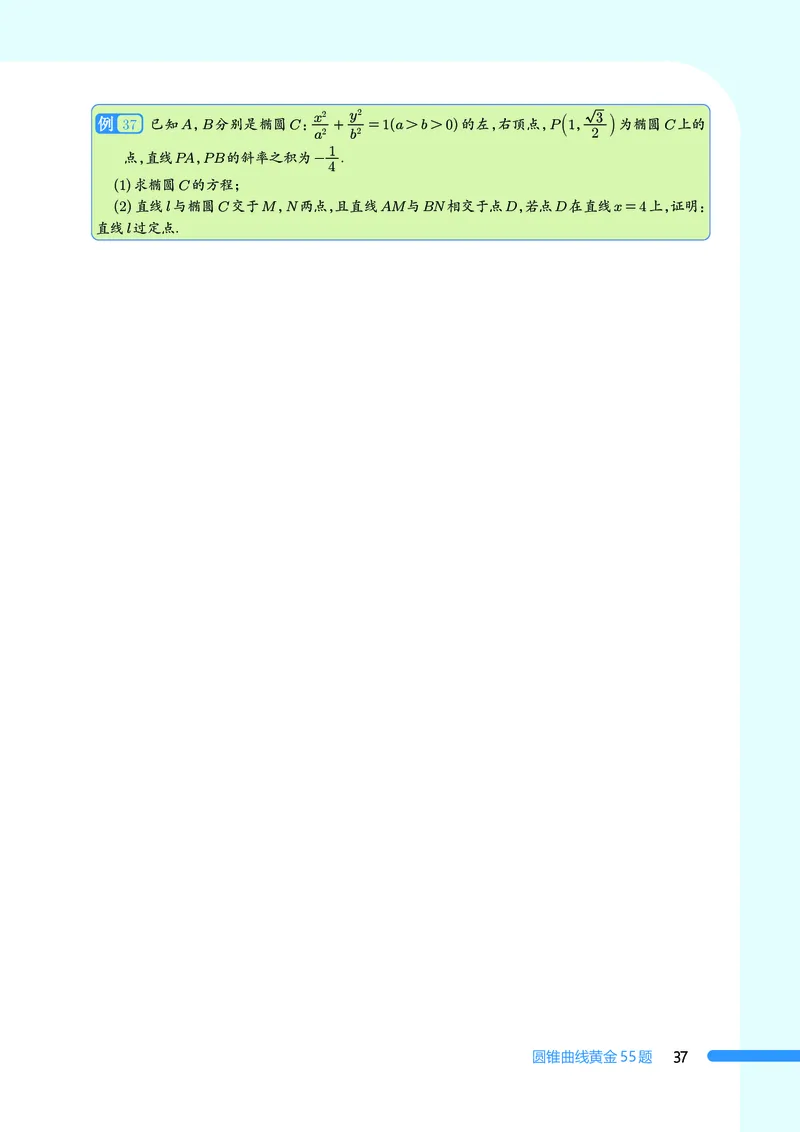
37 已知A,B分别是椭圆C: + =1(a>b>0)的左,右顶点,P1,
a2 b2 2
圆锥曲线黄金55题 37
为椭圆C上的
1
点,直线PA,PB的斜率之积为- .
4
(1)求椭圆C的方程;
(2)直线l与椭圆C交于M,N两点,且直线AM与BN相交于点D,若点D在直线x=4上,证明:
直线l过定点.x2 y2 3
38 已知椭圆 + =1(a>b>0)的焦距为2 3,离心率为 ,椭圆的左右焦点分别为F、
a2 b2 2 1
F,直角坐标原点记为O.设点P(0,t),过点P作倾斜角为锐角的直线l与椭圆交于不同的两点
2
B、C.
(1)求椭圆的方程;
(2)设椭圆上有一动点T,求PT⋅(TF -TF)的取值范围;
1 2
(3)设线段BC的中点为M,当t≥ 2时,判别椭圆上是否存在点Q,使得非零向量OM 与向量
PQ平行,请说明理由.
38 公众号:邦达数学x2 y2
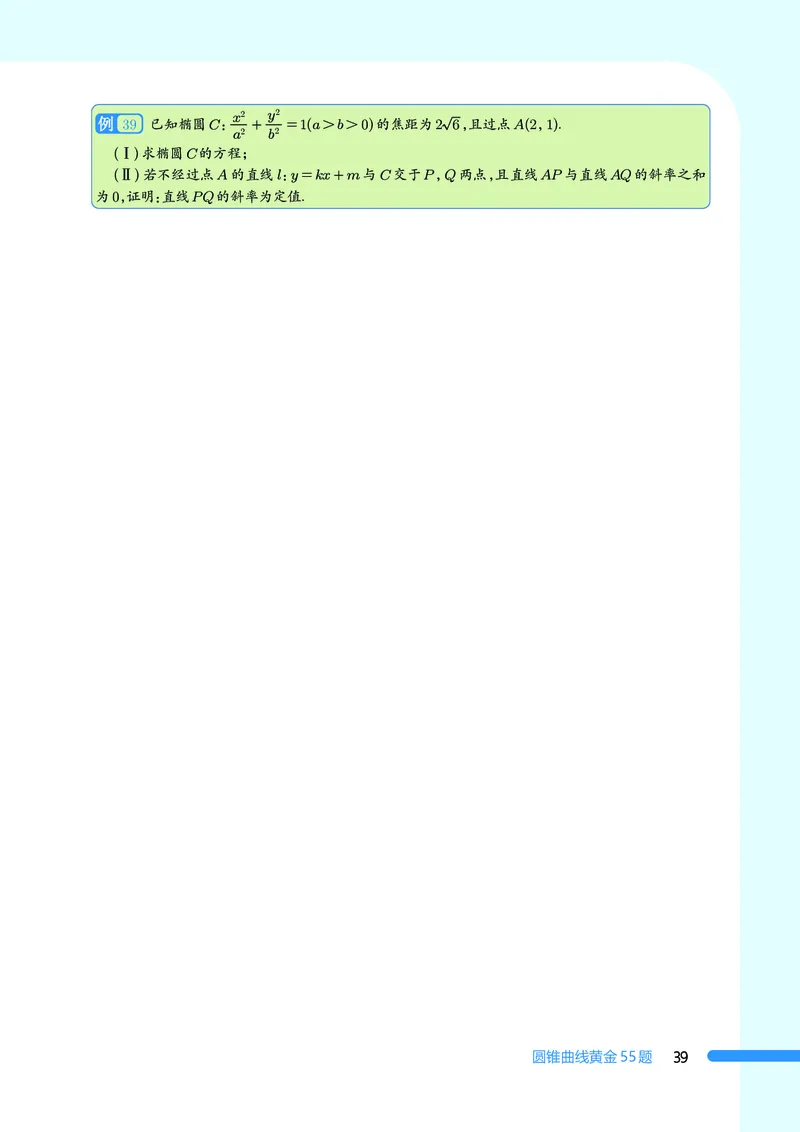
39 已知椭圆C: + =1(a>b>0)的焦距为2 6,且过点A(2,1).
a2 b2
(Ⅰ)求椭圆C的方程;
(Ⅱ)若不经过点A的直线l:y=kx+m与C交于P,Q两点,且直线AP与直线AQ的斜率之和
为0,证明:直线PQ的斜率为定值.
圆锥曲线黄金55题 39x2 y2
40 已知双曲线Γ: - =1,A(2,2)是双曲线Γ上一点.
3 12
(1)若椭圆C以双曲线Γ的顶点为焦点,长轴长为4 3,求椭圆C的标准方程;
(2)设P是第一象限中双曲线Γ渐近线上一点,Q是双曲线Γ上一点,且PA=AQ,求△POQ的面
积S(O为坐标原点);
(3)当直线l:y=-4x+m(常数m∈R)与双曲线Γ的左支交于M、N两点时,分别记直线AM、
AN的斜率为k、k ,求证:k +k 为定值.
1 2 1 2
40 公众号:邦达数学4 12
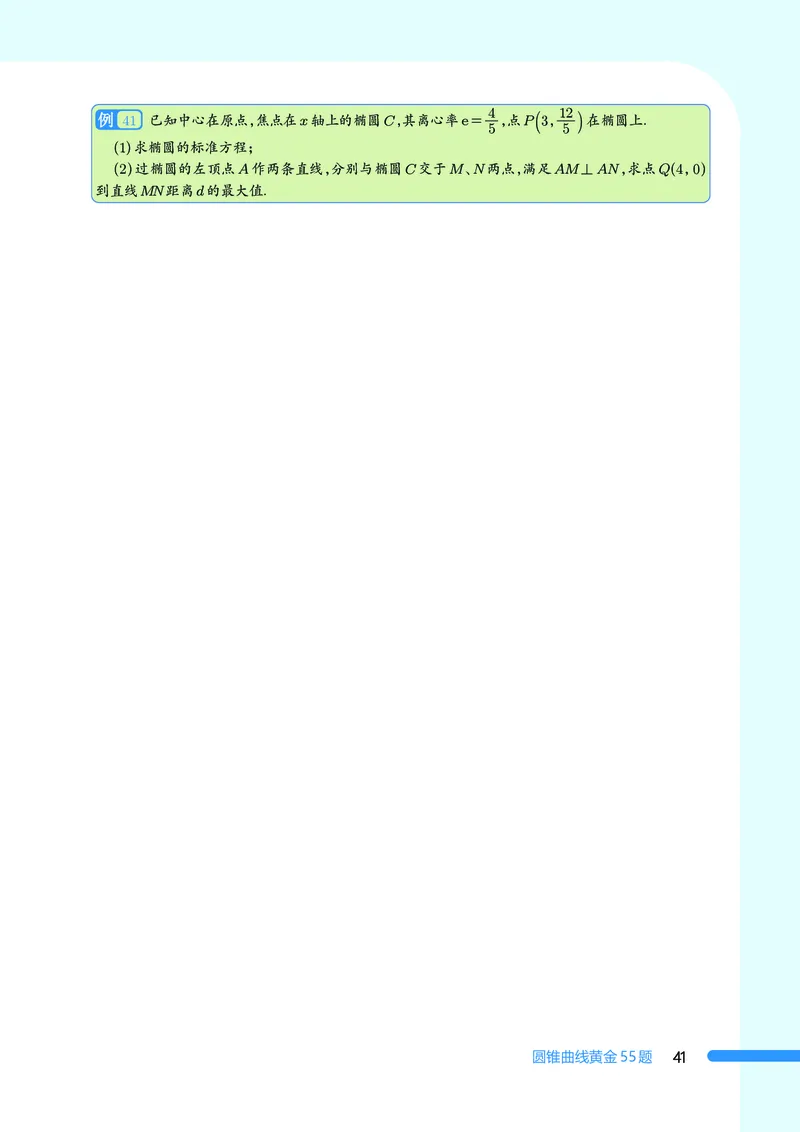
41 已知中心在原点,焦点在x轴上的椭圆C,其离心率e= ,点P3,
5 5
圆锥曲线黄金55题 41
在椭圆上.
(1)求椭圆的标准方程;
(2)过椭圆的左顶点A作两条直线,分别与椭圆C交于M、N两点,满足AM⊥AN,求点Q(4,0)
到直线MN距离d的最大值.42 已知A(0,2),B(0,-2),P为平面上的一个动点.设直线AP,BP的斜率分别为k ,k ,且
1 2
1
满足k ⋅k =- .记动点P的轨迹为曲线C.
1 2 3
(1)求曲线C的方程;
3 1
(2)过点M ,-
2 2
42 公众号:邦达数学
的动直线l与曲线C交于E,F两点.曲线C上是否存在定点N,使得NE
1 1
⊥NF恒成立(直线l不经过点N)?若存在,求出点N的坐标,并求 + 的最小值;若不存
|NE|2 |NF|2
在,请说明理由.x2 y2
43 已知点(2,3)在双曲线C: - =1上.
a2 a2+2
(1)双曲线上动点Q处的切线交C的两条渐近线于A,B两点,其中O为坐标原点,求证:△AOB
的面积S是定值;
1
(2)已知点P ,1
2
圆锥曲线黄金55题 43
,过点P作动直线l与双曲线右支交于不同的两点M、N,在线段MN上取异于
|PM| |MH|
点M、N的点H,满足 = ,证明:点H恒在一条定直线上.
|PN| |HN|44 已知等轴双曲线C的中心为坐标原点O,焦点在x轴上,且焦点到渐近线的距离为 2.
(1)求C的方程;
1 1
(2)若C上有两点P,Q满足∠POQ=45°,证明: + 是定值.
|OP|4 |OQ|4
44 公众号:邦达数学6
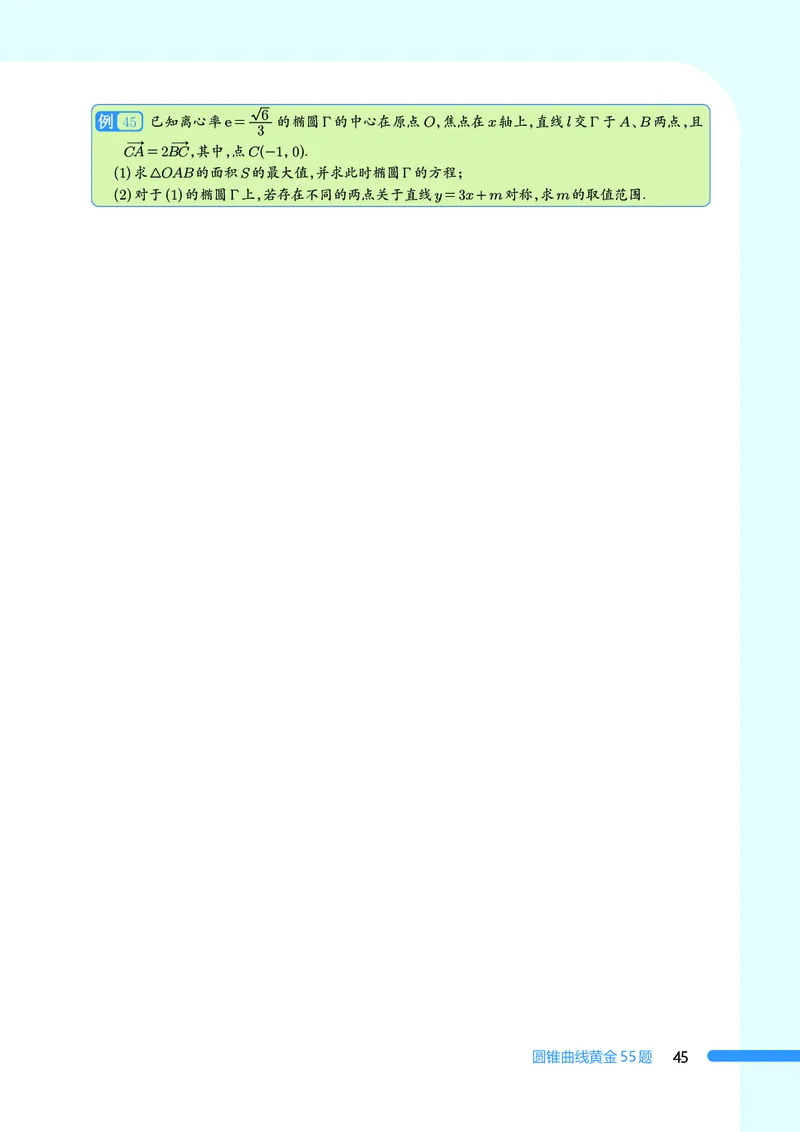
45 已知离心率e= 的椭圆Γ的中心在原点O,焦点在x轴上,直线l交Γ于A、B两点,且
3
CA=2BC,其中,点C(-1,0).
(1)求△OAB的面积S的最大值,并求此时椭圆Γ的方程;
(2)对于(1)的椭圆Γ上,若存在不同的两点关于直线y=3x+m对称,求m的取值范围.
圆锥曲线黄金55题 45x2 y2
46 已知抛物线C:y2=2px(p>0)与椭圆 + =1有公共的焦点.
5 4
(1)求抛物线C的方程;
(2)过Q(-3,-2)的直线l交抛物线C于A,B两点,试问在抛物线C上是否存在定点P,使得直
线PA,PB的斜率存在且非零时,满足两直线的斜率之积为1,若存在.请求出点P的坐标,若不存
在,请说明理由.
46 公众号:邦达数学x2 y2 3
47 椭圆C: + =1(a>b>0)的离心率为 ,过椭圆焦点并且垂直于长轴的弦长度为
a2 b2 2
1.
(1)求椭圆C的标准方程;
(2)若直线l与椭圆C相交于A,B两点,与y轴相交于M(0,m)点,若存在实数m,使得OA+
3OB=4OM,求m的取值范围.
圆锥曲线黄金55题 4748 已知点M为圆O:x2+y2=1上的动点,点F(-2,0),F(2,0),延长FM至N,使得|MN|=
1 2 1
|FM|,线段FN的垂直平分线交直线FN于点P,记P的轨迹为Γ.
1 1 2
(1)求Γ的方程;
(2)直线l与Γ交于A,B两点,且OA⊥OB,求△OAB的面积的最小值.
48 公众号:邦达数学49 有一个半径为4 2的圆形纸片,设纸片上一定点F到纸片圆心E的距离为2 6,将纸片折
叠,使圆周上一点M与点F重合,以点F,E所在的直线为x轴,线段EF的中点O为原点建立平
面直角坐标系.记折痕与ME的交点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)P为曲线C上第一象限内的一点,过点P作圆M:(x+1)2+y2=1的两条切线,分别交y轴于
3
D,H两点,且|DH|= ,求点P的坐标;
2
(3)在(2)的条件下,直线l与曲线C交于A,B两点,且直线PA,PB的倾斜角互补,判断直线AB
的斜率是否为定值?若是,求出该定值;若不是,请说明理由.
圆锥曲线黄金55题 4950 在平面直角坐标系xOy中,动点M在抛物线y2=36x上运动,点M在x轴上的射影为N,动
1
点P满足PN = MN.
3
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)过点D(-3,2)作直线与曲线E顺次交于A、B两点,过点A作斜率为1的直线与曲线E的另
一个交点为点C,求证:直线BC过定点.
50 公众号:邦达数学x2 y2 2 5
51 已知椭圆Γ: + =1(a>b>0)的长轴长为2 5,离心率为 ,斜率为k的直线l与
a2 b2 5
椭圆Γ有两个不同的交点A,B.
(1)求Γ的方程;
(2)若直线l的方程为y=x+t,点M(0,1)关于直线l的对称点N(与M不重合)在椭圆Γ上,求t
的值;
(3)设P(-3,0),直线PA与椭圆Γ的另一个交点为C,直线PB与椭圆Γ的另一个交点为D,若点
7 1
C,D和点Q- ,
3 2
圆锥曲线黄金55题 51
三点共线,求k的值.y2
52 已知双曲线C:x2- =1的左、右焦点分别为F、F,P为双曲线右支上一点.
3 1 2
(1)求双曲线C的离心率;
(2)设过点P和F 的直线l与双曲线C的右支有另一交点为Q,求OP⋅OQ的取值范围;
2
(3)过点P分别作双曲线C两条渐近线的垂线,垂足分别为M、N两点,是否存在点P,使得|PM|
+|PN|= 2?若存在,求出点P的坐标,若不存在,请说明理由.
52 公众号:邦达数学x2 y2 2
53 椭圆E: + =1(a>b>0)的离心率是 ,点M( 2,1)是椭圆E上一点,过点P(0,
a2 b2 2
1)的动直线l与椭圆相交于A,B两点.
(1)求椭圆E的方程;
(2)求△AOB面积的最大值;
|QA| |PA|
(3)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使 = 恒成立?存在,求
|QB| |PB|
出点Q的坐标;若不存在,请说明理由.
圆锥曲线黄金55题 5354 已知动圆过点F(0,1),且与直线l:y=-1相切,设动圆圆心D的轨迹为曲线C.
(1)求曲线C的方程;
(2)过l上一点P作曲线C的两条切线PA,PB,A,B为切点,PA,PB与x轴分别交于M,N两
点.记△AFM,△PMN,△BFN的面积分别为S、S 、S .
1 2 3
(ⅰ)证明:四边形FNPM为平行四边形;
S2
(ⅱ)求 2 的值.
SS
1 3
54 公众号:邦达数学x2 y2
55 已知椭圆C: + =1(a>b>0)的一条准线方程为x=4,长轴长为4,过点P(-2,1)
a2 b2
作直线l交椭圆C于点M、N.
(1)求椭圆C的方程;
1 1
(2)在x轴上是否存在一定点Q,使得直线QM,QN的斜率k ,k 满足 + 为常数?若存在,
1 2 k k
1 2
求出Q点坐标;若不存在,说明理由.
圆锥曲线黄金55题 55