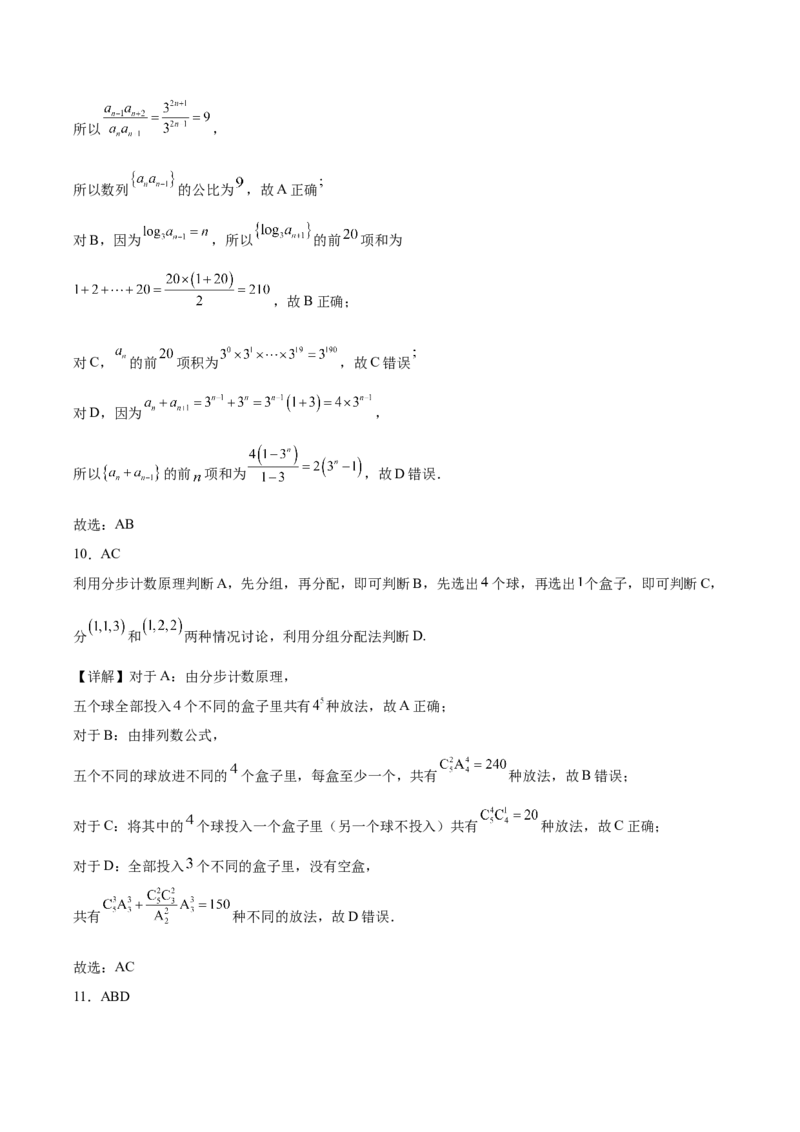文档内容
梅河口市第五中学2024-2025学年高二下学期4月月考
数学试题
一、单选题
1.乘积 的展开式中项数为( )
A.38 B.39 C.40 D.41
2.若 ,则 ( )
A.380 B.190 C.188 D.240
3.投掷一枚质地均匀的骰子两次,记 , ,则
( )
A. B. C. D.
4.若随机变量X的分布列如下:
1 2 3 4
0.1 0.4 0.3
则 ( )
A.0.4 B.0.5 C.0.6 D.0.7
5.若 是离散型随机变量, ,又已知 ,则 的值
为( )
A. B.1 C.2 D.
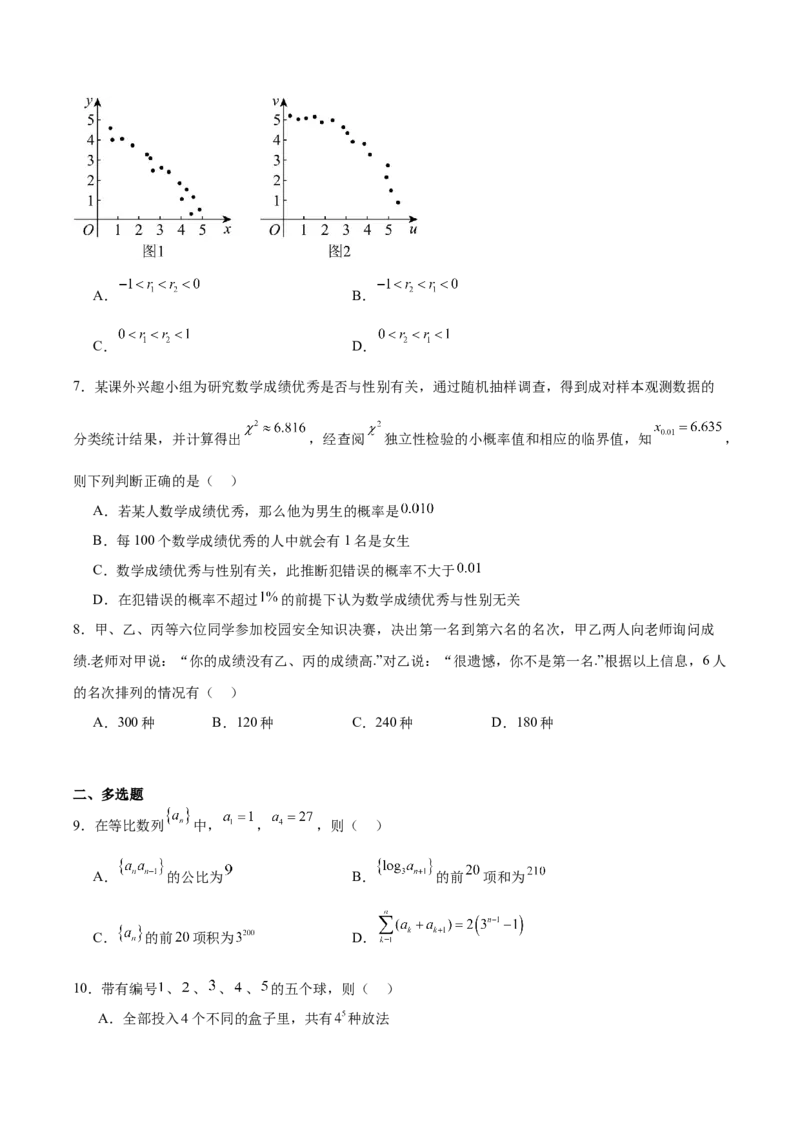
6.根据变量 的观测数据 ,绘制成散点图1;根据变量 的观测数据
,绘制成散点图2.若用线性回归进行分析,设 表示变量 的样本相关系数, 表示
变量 的样本相关系数,则( )A. B.
C. D.
7.某课外兴趣小组为研究数学成绩优秀是否与性别有关,通过随机抽样调查,得到成对样本观测数据的
分类统计结果,并计算得出 ,经查阅 独立性检验的小概率值和相应的临界值,知 ,
则下列判断正确的是( )
A.若某人数学成绩优秀,那么他为男生的概率是
B.每100个数学成绩优秀的人中就会有1名是女生
C.数学成绩优秀与性别有关,此推断犯错误的概率不大于
D.在犯错误的概率不超过 的前提下认为数学成绩优秀与性别无关
8.甲、乙、丙等六位同学参加校园安全知识决赛,决出第一名到第六名的名次,甲乙两人向老师询问成
绩.老师对甲说:“你的成绩没有乙、丙的成绩高.”对乙说:“很遗憾,你不是第一名.”根据以上信息,6人
的名次排列的情况有( )
A.300种 B.120种 C.240种 D.180种
二、多选题
9.在等比数列 中, , ,则( )
A. 的公比为 B. 的前 项和为
C. 的前 项积为 D.
10.带有编号 、 、 、 、 的五个球,则( )
A.全部投入 个不同的盒子里,共有 种放法B.放进不同的 个盒子里,每盒至少一个,共有 种放法
C.将其中的 个球投入 个盒子里的一个(另一个球不投入),共有 种放法
D.全部投入 个不同的盒子里,没有空盒,共有 种不同的放法
11.已知函数 及其导函数 的定义域均为 ,记 ,且 ,
,则( )
A. B. 的图象关于点 对称
C. D. ( )
三、填空题
12.在 的展开式中,所有项的系数和等于 .(用数字作答)
13.已知5道试题中有3道代数题和2道几何题,每次从中抽取一道题,抽出的题不再放回,在第1次抽
到代数题的条件下,第2次抽到几何题的概率为 .
14.已知随机事件 , 有概率 , ,条件概率 ,则 .
四、解答题
15.二项式 的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和.
16.已知椭圆C: (a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不
同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为 时,求k的值.
17.从4名男生和3名女生中任选3人参加演讲比赛,设随机变量 表示所选3人中男生的人数,求:(1) 的分布列以及期望与方差;
(2)设 为事件“抽取的3人中,既有男生,也有女生”,求事件 发生的概率.
18.已知函数 .
(1)当 时,求曲线 在 处的切线方程;
(2)若函数 在区间 上不是单调函数,求 的取值范围;
(3)若 无零点,求 的取值范围.
19.定义:对一个棱锥的各个顶点染色,若每一条棱的两个端点均不同色,则称之为“多彩棱锥”.若用
( )种颜色给某 ( )棱锥染色,出现“多彩棱锥”的数量记作 .
(1)当 , 时,试求 的值;
(2)当 , 时,试求 的值;
(3)结合前两问的解题思路,对任意的正整数 ( ) ( ),请写出 的运算公式,并证明.
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D B B A C D AB AC
题号 11
答案 ABD
1.C
采用分步乘法计数原理进行计算即可.
【详解】从第一个括号中选一个字母有2种方法,从第二个括号中选一个字母有4种方法,从第三个括号
中选一个字母有5种方法,根据分步乘法计数原理可知共有 项.
故选:C.
2.B
利用组合数的性质求出 ,再求出答案.
【详解】由 ,得 ,所以 .
故选:B
3.D分别写出事件 和事件 包含的基本事件,由条件概率计算公式得到 .
【详解】记事件 ,包含的基本事件数是 , , ,共3个基本事件,
事件 ,包含的基本事件数是 , ,共2个基本事件,
所以 .
故选:D.
4.B
根据题意,由分布列的性质可得 的值,然后代入计算,即可得到结果.
【详解】由题可得 ,解得 .
由 ,可得 或4,
则 ( 或 ) .
故选:B
5.B
先得到随机变量 的值只能为 ,根据期望和方差得到方程组,求出方程的解,得到答案.
【详解】 ,故随机变量 的值只能为 ,
,解得 或 ,
所以 .
故选:B
6.A
根据散点图,结合相关系数知识即可得出答案.
【详解】由图可得 随 增大而减小, 随 增大而减小,
所以 与 增呈负相关关系, 与 呈负相关关系,故 ,又由图可知图1相关性更强,故 更接近 ,
所以 .
故选:A.
7.C
根据独立性检验的定义判断即可.
【详解】因为 ,
所以数学成绩优秀与性别有关,此推断犯错误的概率不大于 ,
即在犯错误率不超过 的前提下认为“数学成绩优秀与性别有关”,故C正确,D错误;
若某人数学成绩优秀,由已知数据不能判断他为男生的概率,故A错误;
每 个数学成绩优秀的人中可能没有女生,也有可能有多名女生,由已知数据不能确定结论,故B错误;
故选:C.
8.D
根据师生对话,结合三人的相对名次,利用插空法进行求解即可.
【详解】因为老师对甲说:“你的成绩没有乙、丙的成绩高,
所以有两种相对名次,一是乙、丙、甲,二是丙、乙、甲,
因此不同的名次有 种可能;
老师对乙说:“很遗憾,你不是第一名,
当乙是第一名时,有甲没有丙的名次高,这时不同的名次有 种可能,
因此6人的名次排列的情况有 种可能,
故选:D
9.AB
对A,根据等比数列的基本量关系,结合等比数列的定义判断即可;对B,由A可得 ,再根据
等差数列求和公式求解即可;对C,根据 求解即可;对D,代入 求解即可.
【详解】对A,设等比数列 的公比为 ,则 ,得 ,
所以 ,所以 ,所以 ,
所以数列 的公比为 ,故A正确
对B,因为 ,所以 的前 项和为
,故B正确;
对C, 的前 项积为 ,故C错误
对D,因为 ,
所以 的前 项和为 ,故D错误.
故选:AB
10.AC
利用分步计数原理判断A,先分组,再分配,即可判断B,先选出 个球,再选出 个盒子,即可判断C,
分 和 两种情况讨论,利用分组分配法判断D.
【详解】对于A:由分步计数原理,
五个球全部投入 个不同的盒子里共有 种放法,故A正确;
对于B:由排列数公式,
五个不同的球放进不同的 个盒子里,每盒至少一个,共有 种放法,故B错误;
对于C:将其中的 个球投入一个盒子里(另一个球不投入)共有 种放法,故C正确;
对于D:全部投入 个不同的盒子里,没有空盒,
共有 种不同的放法,故D错误.
故选:AC
11.ABD对于A,对条件 ,求导可得;对于B,对条件 ,两边同时除以 可得;
对于C,反证法,假设C正确,求导,结合条件 ,可得 与 矛盾,可判断
C;对于D,求出 , ,所以有 , , ,得出数列
是以0为首项, 为公差的等差数列,利用等差数列求和公式即可判断.
【详解】因为 ,
所以 ,即 ,
令 ,得 ,故A正确;
因为 ,
当 时, ,
所以 的图象关于点 对称,故B正确;
对于C,假设 成立,
求导得 ,
即 ,又 ,
所以 ,所以 与 矛盾,故C错误;
对于D,因为 , ,
所以 , , , ,
所以有 ,
所以数列 的奇数项是以 为首项, 为公差的等差数列,
数列 的偶数项是以 为首项, 为公差的等差数列,
又 , ,
所以数列 是以 为首项, 为公差的等差数列,所以 ,
所以 ,故D正确.
故选:ABD.
12.
【详解】由题意,
在 中,当 时所求值即为所有项的系数和,为: ,
故答案为: .
13. /0.5
设事件A:第1次抽到代数题,事件B:第2次抽到几何题,求得 ,结合条件概率的计算公式,
即可求解.
【详解】从5道试题中有3道代数题和2道几何题,每次从中抽取一道题,抽出不再放回,
设事件A:第1次抽到代数题,事件B:第2次抽到几何题,
则 , ,
所以在第1次抽到代数题的条件下,第2次抽到几何题的概率为 .
故答案为: .
14.0.82
根据条件概率公式计算即可.
【详解】∵ ,∴ , .
由乘法公式得 .
∴ .
故答案为:0.82.
15.(1) ;(2) ;(3) .【解析】(1)根据二项式系数的性质即可求解;
(2)设 ,令 ,代入 即可求解;
(3)由(2),再令 ,两式相加即可求解.
【详解】设 .
(1)二项式系数之和为 .
(2)各项系数之和为 ,
令 ,得 .
(3)由(2)知 ,①
令 ,
得 ,②
将①②两式相加,得 ,
此即为所有奇数项系数之和.
16.(1) (2)1或-1.
【详解】
(1)由题意得 解得 .所以椭圆C的方程为 .
(2)由 得 .设点M,N的坐标分别为 , ,则 , , ,
.
所以|MN|= = = .
由因为点A(2,0)到直线 的距离 ,
所以△AMN的面积为 . 由 ,解得 ,经检验
,所以 .
17.(1)分布列见解析,期望 ,方差
(2)
(1)利用超几何分布可求X的分布;进而利用期望与方差公式可求解;
(2)利用 可求解.
【详解】(1)随机变量X的所有可能取值为0,1,2,3,
所以,随机变量X的分布列为
0 1 2 3随机变量 的数学期望 ,
方差
(2)设 ,
所以,事件 发生的概率为 .
18.(1)
(2)
(3)
【详解】(1) 时, ,
所以 在 处的切线方程为
(2)因为 在区间 上不是单调函数,
所以 在 上有变号解,即 在 上有变号解.
因为 ,所以 ,所以
(3)因为 ,
当 ,即 时, ,
所以 在 上单调递减,
因为 ,所以 在 上无零点,符合题意;.
当 时,令 ,则 ,
当 时, ,当 时, ,
所以 的单调递减区间是 ;单调递增区间是 ,
所以 的最小值为
当 ,即 时, 无零点,符合题意;
当 时, 有一个零点 ,此时 ,不符合题意;
当 时, 的最小值 ,
因为 ,
所以 ,使得 ,不符合题意;
综上所述,当 时,
无零点.
19.(1)1560
(2)6120
(3) ,证明见解析
【详解】(1)题目等同于“用六种不同的颜色给一个四棱锥的每个顶点染上一种颜色,
并使同一条棱的两个端点异色”,设顶点为 ,底面4点为 , , , .
首先对顶点 进行涂色,共有6种选择;
第二步,对 点进行涂色,共有5种涂色方法;
第三步,需要对 是否同色进行分类:
若 同色,则共有 种情况;
若 不同色,则共有 种情况;
因此, 种情况.
(2)题目等同于“用六种不同的颜色给一个五棱锥的每个顶点染上一种颜色,
并使同一条棱的两个端点异色”,
设顶点为 ,底面五点为 , , , , .
首先对顶点 进行涂色,共有6种选择;
此时 五点共有五种不同颜色可供选择.
故问题转化为如图 , , , , 五个区域,
有5种不同的颜色可用,要求相邻区域不能涂同一种颜色,即5色5区域的环状涂色问题.
若按照 , , , , 的顺序分步涂色,暂不考虑 同色的情况,
则共有 种情况;其中包含了 同色.
当 同色时,相当于(1)中 四个点的涂色问题,即有1560种;
因此, .
(3)题目等同于“用 种不同的颜色给一个 棱锥的每个顶点染上一种颜色,
并使同一条棱的两个端点异色”,设顶点为 ,底面五点为 , , , ,
首先对顶点 进行染色,共有 种选择;
设 , , , , 的染色方法共有 种,
下面考虑 的递推关系:
若从 开始染色,则 有 种染法,
继而 , , , 分别均有 种染法,最后对 染色,
如果仅要求 与 异色(不要求 与 异色),则仍有 种染法.
于是,总共有 种染法.
上述 种染法可分为以下两类:
一类是 与 异色,这是符合要求的,有 种染法;
另一类是 与 同色,这不符合要求,
这时可将 与 合并成一点,得出 种符合题设的染法.
于是 ( ),
即 .
故
得