专题04分段数列（解析版）_2024-2025高三（6-6月题库）_2025年02月试卷_02272025年高考数学压轴大题必杀技系列·数列

专题 4 分段数列 新高考在试题形式、试卷结构、难度调控等方面深化改革,数列解答题的难度增加,作为压轴题出现 的概率变大,由于分段数列问题大多涉及分类讨论思想,对能力要求更高,作为压轴题出现的频率更高,本专 题总结分段数列的常见类型及求解,供大家参考. （一）分段数列求通项 分段数列求通项,关键是确定n在不同范围内取值时 与 的关系,恰当进行分类是求解的难点. 【例1】（2024届四川省成都石室中学高三下学期适应性考试）已知数列 满足 当 时, (1)求 和 ,并证明当 为偶数时 是等比数列； (2)求 及 . 【解析】（1）因为 当 时, , 所以 , . , ,又 , 当 为偶数时, 是以 为首项,以 为公比的等比数列； （2）由（1）知, , 学科网（北京）股份有限公司设 ,则 为偶数时, 当 为奇数时, ； 设 , 为奇数时, , 所以 . . （二）分段数列求和 对于分段数列求和,一般数列分几段,求和时也分几段,对于 型的数列求和,一定要 注意若 为偶数,则奇数项与偶数项各有 项,若n为奇数,则奇数项有 项,偶数项有 ,若 是公 差为 的等差数列,则 的奇数项是公差为 的等差数列,若 是公比为 的等比数列,则 的偶数 项是公比为 的等比数列. 【例2】（2024届广东省名校教研联盟高三下学期5月模拟）已知数列 是公差不为0的等差数列,其前 n项和为 , , , , 成等比数列． (1)求 的通项公式； (2)若 , ,求数列 的前100项和 ． 学科网（北京）股份有限公司【解析】（1）设数列 的首项为 ,公差为 , 根据题意得 即 解得 或 ． 又因 ,所以 ．所以 的通项公式为 ． （2）由（1）得 ． 即数列 的偶数项是以4为首项,4为公差的等差数列, 奇数项是以 为首项,16为公比的等比数列． 数列 的前100项中偶数项有50项,奇数项有50项, 数列 的前100项和 ． , ． 所以 ． 【例3】（2024届湖南省长沙市第一中学高考最后一卷）若各项均为正数的数列 满足 （ 为常数）,则称 为“比差等数列”.已知 为“比差等数列”,且 . 学科网（北京）股份有限公司(1)求 的通项公式； (2)设 ,求数列 的前 项和 . 【解析】（1）由 为“比差等数列”, 得 ,从而 . 设 ,则 , 所以数列 为等差数列. 因为 ,所以 为常数列, 因此, ,即 , 所以 是首项为 ,公比为 的等比数列,因此 . （2）当 为偶数时, ； 当 为奇数时, . 综上, . 学科网（北京）股份有限公司（三） 型的分段数列 此类问题比较简单,求解时只需分n为偶数与奇数即可,求指定项时要注意区分该项在奇数项或偶数项中的位 置,求和时要注意奇数项与偶数项的项数. 【例4】已知数列 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列 前 项和为 ,且满足 (1)求 ； (2)求数列 的通项公式及数列 的前2k项和 ; (3)在数列 中,是否存在连续的三项 ,按原来的顺序成等差数列?若存在,求出所有满足条件的 正整数 的值;若不存在,说明理由 【解析】（1）设等差数列的公差为 ,等比数列的公比为 , 则 , 因为 ,所以 ,即 , 因为 ,所以 ,即 , 解得 , 所以 ； （2）由（1）知 , 所以对于 ,有 , , 所以 （ ）, 学科网（北京）股份有限公司（3）在数列 中,仅存在连续三项 按原来的顺序成等差数列,此时正整数 , 下面说明： 若 ,则由 ,得 , 化简得 , 此式左边是偶数,右边是奇数,不可能成立, 若 ,则由 ,得 ,化简得 , 令 ,则 , 所以 ,所以只有 ,此时 , 综上,在数列 中,仅存在连续三项 按原来的顺序成等差数列,此时正整数 . （四） 型的分段数列 求解此题问题,一般是由已知条件推出 与 （或 与 , 与 ）的递推关系,再构造等 差（比）数列求通项. 【例5】设数列 满足： 是 的等比中项. （1）求 的值； （2）求数列 的前20项的和. 【解析】（1）由已知 , , 又 是 的比例中项,所以 ,即 ,显然 且 ,故解得 ； （2） 是奇数时, , , ,而 , 学科网（北京）股份有限公司所以数列 是等比数列, ． （五）相邻项和（积）为等差（比）数列型的分段数列 1.若 ,则当 时, ,两式相减得 ,即数列 与数列 均是公差为 的等差数列. 2.若 ,则 ,两式相除得 ,即数列 与数列 均是 公比为 的等比数列. 【例6】设数列 的前n项和为 ,且 ． （1）求 ； （2）若 对 恒成立,求 的取值范围． 【解析】（1）因为 ,当 时, , 两式相减得 ,则 , 两式相减得 ． 当 时, ,则 ；当 时, ,则 , 所以 . （2）由（1）得 ． 要使 对 恒成立,则 即 解得 , 学科网（北京）股份有限公司所以 的取值范围为 . （六） 型的分段数列 求解此类问题,关键是确定分界点 . 【例7】（2023年高考全国乙卷数学真题）记 为等差数列 的前 项和,已知 ． (1)求 的通项公式； (2)求数列 的前 项和 ． 【解析】（1）设等差数列的公差为 , 由题意可得 ,即 ,解得 , 所以 , （2）因为 , 令 ,解得 ,且 , 当 时,则 ,可得 ； 当 时,则 ,可得 ； 综上所述： . 【例8】（2024届吉林省长春市东北师大附中高三第六次模拟）记集合 无穷数列 中存在有限 项不为零, ,对任意 ,设 ．定义运算 若 , 学科网（北京）股份有限公司则 ,且 ． (1)设 ,用 表示 ； (2)若 ,证明： ： (3)若数列 满足 ,数列 满足 ,设 , 证明： ． 【解析】（1）因为 ,所以 , 所以 , 根据多项式的乘法可得： ． （2）因为 , 所以 ． 又 , 所以 , 所以 （3）对于 , 因为 ,所以 , 所以 , 所以 , 学科网（北京）股份有限公司所以 ． 所以 ． 所以 ． 所以 (七)含 或 型的分段数列 求解含 或 型的分段数列问题,一般借助三角函数的周期性求解,求和时通常把一个周期内的项 求和后,构造新数列求解. 【例9】（2024届山东潍坊高三三模）已知正项等差数列 的公差为2,前 项和为 ,且 成等比数列. (1)求数列 的通项公式 ； (2)若 求数列 的前 项和. 【解析】（1）因为 , 所以 ,即 ,解得 或 , 学科网（北京）股份有限公司又因为 ,所以 ,所以 . （2） ,所以 , 所以 为奇数时, , 为偶数时, , 所以前 项和 . (八)当 时 型的分段数列 求解此类问题的关键是判断在每个范围内数列项的个数. 【例10】已知数列 是等差数列,其前 和为 , , ,数列 满足 (1)求数列 , 的通项公式； (2)若对数列 , ,在 与 之间插入 个2（ ）,组成一个新数列 ,求数列 的前83项的 和 . 【解析】（1）设公差为 ,故 ,解得 , 故 , 故 ,① 学科网（北京）股份有限公司当 时, , 当 时, ,② 式子①-②得, , 即 ,当 时, 也满足上式,故 ； （2）因为 ,所以在 中,从项 开始,到项 为止, 共有项数为 , 当 时, ,当 时, , 故数列 前 项是项 之后还有 项为2, . 【例11】（2023年天津高考数学真题）已知 是等差数列, ． (1)求 的通项公式和 ． (2)设 是等比数列,且对任意的 ,当 时,则 , （Ⅰ）当 时,求证： ； （Ⅱ）求 的通项公式及前 项和． 【解析】（1）由题意可得 ,解得 , 则数列 的通项公式为 , 求和得 学科网（北京）股份有限公司. （2）(Ⅰ)由题意可知,当 时, , 取 ,则 ,即 , 当 时, , 取 ,此时 , 据此可得 , 综上可得： . 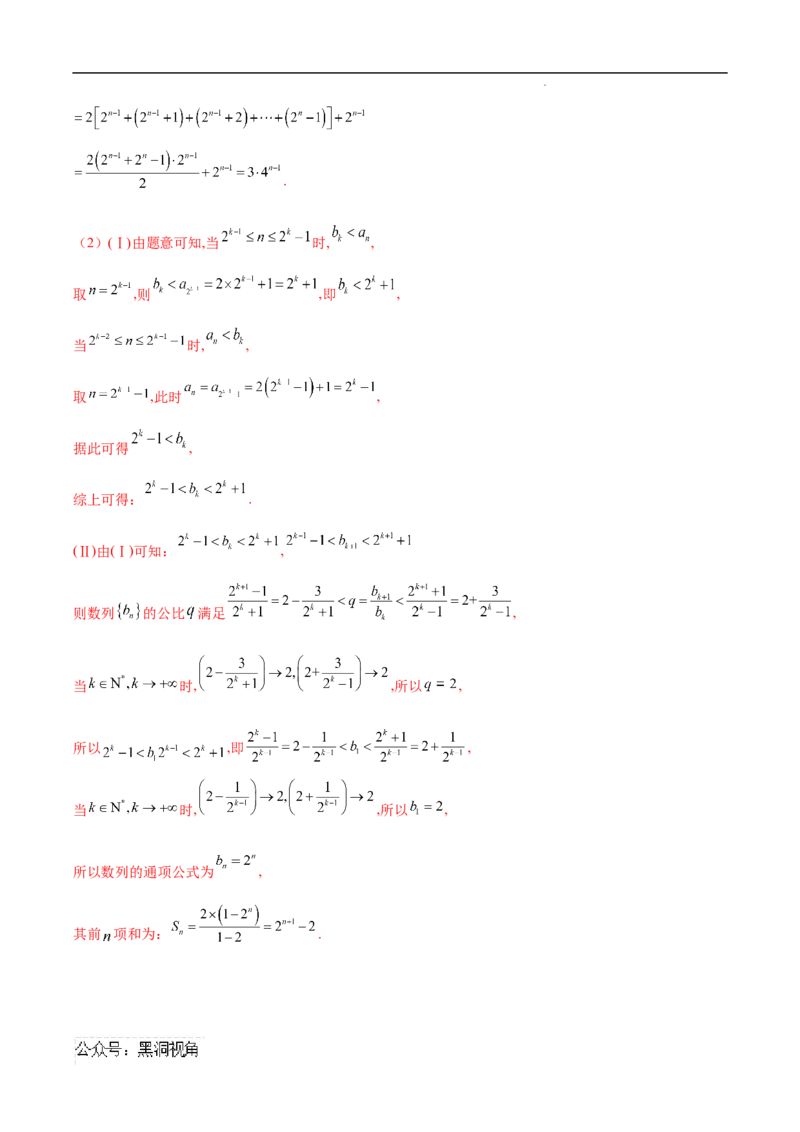(Ⅱ)由(Ⅰ)可知： , 则数列 的公比 满足 , 当 时, ,所以 , 所以 ,即 , 当 时, ,所以 , 所以数列的通项公式为 , 其前 项和为： . 学科网（北京）股份有限公司【例1】（2024届湖南省邵阳市高三第三次联考）已知数列 , ,函数 ,其中 , 均为实数． (1)若 , , , , , （ⅰ）求数列 的通项公式； （ⅱ）设数列 的前 项和为 ,求证： ． (2)若 为奇函数, , , 且 ,问：当 时, 是否存在整数 ,使得 成立．若存在,求出 的最大值；若不存在,请说明理由．（附： , ） 【解析】（1）（ⅰ） , , 由 , 得 ,解得 , 又 , , 学科网（北京）股份有限公司, 是以2为公比,2为首项的等比数列． ． （ⅱ）令 ,则 , ． 显然,当 时, 是递增数列, 在 时,单调递减, 可得 , ． ． （2） 为奇函数, ． , 又 , , , ． , 由 得, ． , , , , 学科网（北京）股份有限公司在 上为增函数, 当 时, , ； , ． 当 时, ． 时, ,又 , 当 时, , ． 又 , 的最大值为5． 【例2】（2023年新课标全国Ⅱ卷数学真题）已知 为等差数列, ,记 , 分别为数 列 , 的前n项和, , ． (1)求 的通项公式； (2)证明：当 时, ． 【解析】（1）设等差数列 的公差为 ,而 , 则 , 于是 ,解得 , , 所以数列 的通项公式是 . 学科网（北京）股份有限公司（2）方法1：由（1）知, , , 当 为偶数时, , , 当 时, ,因此 , 当 为奇数时, , 当 时, ,因此 , 所以当 时, . 方法2：由（1）知, , , 当 为偶数时, , 当 时, ,因此 , 当 为奇数时,若 ,则 ,显然 满足上式,因此当 为奇数时, , 当 时, ,因此 , 所以当 时, . 【例3】（2024年天津高考数学真题）已知数列 是公比大于0的等比数列．其前 项和为 ．若 ． (1)求数列 前 项和 ； 学科网（北京）股份有限公司(2)设 , ． （ⅰ）当 时,求证： ； （ⅱ）求 ． 【解析】（1）设等比数列 的公比为 , 因为 ,即 , 可得 ,整理得 ,解得 或 （舍去）, 所以 . （2）（i）由（1）可知 ,且 , 当 时,则 ,即 可知 , , 可得 , 当且仅当 时,等号成立,所以 ； （ii）由（1）可知： , 若 ,则 ；若 ,则 , 当 时, ,可知 为等差数列, 学科网（北京）股份有限公司可得 , 所以 , 且 ,符合上式,综上所述： . 【例4】（2021年新高考1卷数学真题）已知数列 满足 , （1）记 ,写出 , ,并求数列 的通项公式； （2）求 的前20项和. 【解析】（1）由题设可得 又 , ,故 即 即 所以 为等差数列,故 . （2）设 的前 项和为 ,则 ,因为 , 所以 . 【例5】（2024届湖南长沙高三下学期三模）若各项均为正数的数列 满足 （ 为常数）,则称 为“比差等数列”.已知 为“比差等数列”,且 . (1)求 的通项公式； 学科网（北京）股份有限公司(2)设 ,求数列 的前 项和 . 【解析】（1）由 为“比差等数列”, 得 , 从而 . 设 ,则 , 所以数列 为等差数列. 因为 , 所以 为常数列, 因此, ,即 , 所以 是首项为 ,公比为 的等比数列, 因此 . （2）当 为偶数时, ； 当 为奇数时, . 学科网（北京）股份有限公司综上, . 【例6】设 是数列 的前n项和,已知 , （1）证明： 是等比数列； （2）求满足 的所有正整数n. 【解析】（1）由已知得 , 所以 ,其中 , ,所以 是以 为首项, 为公比的等比数列； （2）由（1）知 ,所以 , , 所以 ,所以 ,当 时, 单调递减,其中 , , , 所以满足 的所有正整数n为1,2. 1.（2024届福建省厦门市高三第四次质量检测）设 为数列 的前 项和,已知 ,且 为等 差数列. 学科网（北京）股份有限公司(1)求 的通项公式； (2)若 ,求 的前 项和 . 【解析】（1）设等差数列 的公差为 ,因为 , 所以 ,即 , 所以 ,即 , 当 时, , 当 时, ,满足上式,所以 . （2）由（1）知 则 所以数列 的前 项和为 . 2．（2024届重庆市第八中学校高三下学期5月月考）已知数列 满足 , ． (1)求 , , ,并求证： ； 学科网（北京）股份有限公司(2)求数列 的前2n项和 ． 【解析】（1） , , , 证明： , , 即 , ,则 , 故 ． （2）由（1）可得： 且 , 所以数列 是公比为2的等比数列, 故 ,解得： , , 故 所以 ． 3．（2024届贵州省贵阳市第一中学等校高三下学期三模）已知正项数列 的前 项和为 ,且满足 .试求: (1)数列 的通项公式; 学科网（北京）股份有限公司(2)记 ,数列 的前 项和为 ,当 时,求满足条件的最小整数 . 【解析】（1）因为 ,当 时, , 当 时, ,因为 , 两式相减得, ,因为 ,所以 , 所以 , 均为等差数列, , ． 所以 ； （2）由题意得, , 所以 , 因为 ,所以 , 解得 ．所以满足条件的最小整数 为9． 4．（2024届天津市武清区杨村第一中学高考热身练）已知数列 是正项等比数列, 是等差数列,且 , (1)求数列 和 的通项公式; (2) ,求数列 的前 项和. (3) 表示不超过 的最大整数, 表示数列 的前 项和,集合 共有 4个元素,求 范围; 【解析】（1）设等比数列 的公比为 ,等差数列 的公差为 , 学科网（北京）股份有限公司因为 , 则 ,解得 或 （舍去）, 所以 ； . （2）因为 , , 设 , , 两式相减得 , 所以 , 当n为奇数时, , 设 , . （3）由题意可知： , 学科网（北京）股份有限公司其中 , 所以 , 集合 ,设 , 则 , 所以当 时, ,当 时, ． 计算可得 , , , , , 因为集合有4个元素, ． 5．（2024届天津市第一中学高三第五次月考）已知数列 是等差数列, , ,数列 的前n项和为 ,且 , (1)求数列 和 的通项公式； (2)若集合 中恰有四个元素,求实数 的取值范围； (3)设数列 满足 , 的前n项和为 ,证明： ． 【解析】（1）设等差数列 的公差为 , 由题意可得： ,解得 , 所以 ；又因为 , 若 ,可得 ,解得 ；若 ,可得 , 学科网（北京）股份有限公司两式相减得 ,即 ； 可知数列 是以首项 ,公比 的等比数列,所以 . （2）由（1）可知： , 若 ,即 ,可得 , 设 ,原题意等价于关于n的不等式 恰有4个不同的解, 令 , 当且仅当 时,等号成立, 可得 ,且 ,则 , 所以实数 的取值范围为 . （3）由题意可知： ,则 , 则 , 因为 ,则 ,即 ,可得 , 则 ； 又因为 ,则 ,可得 , 学科网（北京）股份有限公司则 ； 综上所述： . 6．（2024届山西省高考三模）已知等差数列 的公差 ,前 项和为 ,且 , . (1)求数列 的通项公式； (2)若 ,求数列 的前 项和 . 【解析】（1）因为 , , 所以 ,解得 或 , 因为 ,所以 ,则 ； （2）由（1）可得 , 所以 . 7．（2024届福建省厦门市高三第二次质检）已知 为等差数列 的前n项和, , , . 学科网（北京）股份有限公司(1)求 的通项公式； (2)记 为数列 的前n项和,若 ,求n的最小值. 【解析】（1）设数列 的公差为d, 依题意, , 即 ,解得 , 所以 的通项公式是 . （2）由（1）知 ,所以 , , 恒成立, 令 , 由 ,由于 ,所以 . 所以 所以 的最小值为4. 8．（2024届天津市十二区重点学校高三下学期联考）设 是等差数列,其前 项和 , 是等比数列,且 , , . (1)求 与 的通项公式； 学科网（北京）股份有限公司(2)设 ,求数列 的前 项和 ； (3)若对于任意的 不等式 恒成立,求实数 的取值范围. 【解析】（1）设等差数列 的公差为 ,等比数列 的公比为 , 由 , ,又 , , , 由 , ,又 , , , , , 即 , ． （2）当 为奇数时, , 记 ,则有 , , 得： , , , 当 为偶数时, , 记 , 学科网（北京）股份有限公司, ． （3）由 与 恒成立, 可得 恒成立, 恒成立,即求 的最大值, 设 , , 单调递增, 又 , , ． 9．（2024届山东省烟台市高三二模）已知 是公差不为0的等差数列,其前4项和为16,且 成等 比数列. (1)求数列 的通项公式； (2)设 ,求数列 的前 项和 . 【解析】（1）设 的公差为 ,由题意知 ,即 , 学科网（北京）股份有限公司即有 ,因为 ,可得 , , 所以 ； （2）设数列 的前 项中的奇数项之和为 ,偶数项之和为 , 则 , , 所以 ． 10．已知等差数列 的前 项和为 , . (1)求数列 的通项公式 ； (2)求数列 的前 项和 . 【解析】（1） 时, , 时, , 又 , 学科网（北京）股份有限公司所以 ； （2）由（1） , 当 时, , 当 时, , . 11．已知 的前 项和是 ,且 ． (1)求数列 的通项公式； (2)设 求数列 的前 项和 ． 【解析】（1）由 ①得,当 时, ②, 联立①②得 , 所以有 , 因为 ,所以 ． （2）设数列 的前 项中的奇数项之和为 ,偶数项之和为 , 由（1）知 则 , 学科网（北京）股份有限公司, 综上： ． 12．已知正项数列 的前 项和为 ,且满足 . (1)求数列 的通项公式； (2)若 的前 项和为 ,求 . 【解析】（1）因为 ①, 时, ②, ①-②整理得 , 数列 是正项数列, , 当 时, , , 数列 是以1为首项,2为公差的等差数列, ； （2）由题意知,设 的前 项中奇数项的和为 ,偶数项的和为 , , , 学科网（北京）股份有限公司. 13.已知等差数列{a}的前n项和为S,a＝－9,a 为整数,且a≤0,a≥0. n n 1 2 5 6 (1) 求{a}的通项公式； n (2) 设b 1 ＝,b n＋1 ＝(n∈N*),求{b n }的前n项和T n . 【解析】 设{a}的公差为d,由题意得 n 所以≤d≤.因为a∈Z,所以d＝2, 2 所以a＝2n－11. n (2) 设b 1 ＝,b n＋1 ＝(n∈N*),求{b n }的前n项和T n . 由题可知,当n为偶数时,b＋b ＝(－2)n＝2n. n n＋1 ①当n为奇数(n≥3)时,T＝b＋(b＋b)＋(b＋b)＋…＋(b ＋b)＝b＋22＋24＋…＋2n－1＝＋＝. n 1 2 3 4 5 n－1 n 1 当n＝1时也符合上式． ②当n为偶数时, T＝T ＋b＝＋a ＝＋2n－13. n n－1 n n－1 所以T＝ n 14.（2020天津高考真题）已知 为等差数列, 为等比数列, ． （Ⅰ）求 和 的通项公式； （2）对任意的正整数 ,设 求数列 的前 项和． 【解析】(1)设等差数列 的公差为 ,等比数列 的公比为q. 由 , ,可得d=1. 从而 的通项公式为 . 由 , 又q≠0,可得 ,解得q=2, 从而 的通项公式为 . 学科网（北京）股份有限公司(2)当n为奇数时, , 当n为偶数时, , 对任意的正整数n,有 , 和 ① 由①得 ② 由①②得 , 由于 , 从而得： . 因此, . 所以,数列 的前2n项和为 .  2a 1,当n为奇数时  n 15.（2024届广东省广州实验中学校考）已知数列 满足a 1 ,且 的前100 a n  n1  2 a n 3,当n为偶数时 a n  项和S 3775 100 (1)求 a  的首项a ； n 1 1 3 (2)记 b n  a 2n1 a 2n ,数列b n 的前 n 项和为 T n ,求证：T n  2 . 学科网（北京）股份有限公司1 【解析】（1）当 为奇数时,a 2a 12 a 31a 2； n n1 n 2 n1 n1 则偶数项构成以2为公差的等差数列, 所以当n为偶数时,a a n2； n 2 1 1 当 n 为偶数时,a n1  2 a n 3 2   2a n1 13  a n1 1, 则奇数项构成以1为公差的等差数列, n1 所以当 为奇数时,a a  , n n 1 2  n1 a  ,当n为奇数时 则a  1 2 ,又 , n  a n2,当n为偶数时 a 2a 1 2 2 1 所以S a a a a a a 150a 36253775, 100 1 3 99 2 4 100 1 解得,a 1. 1 3 （2）由（1）得, , ,T b 1 , a n a 2n1 1 1 2 2n1 2n 1 1 1 1 1 1 当 时, b       , n2 n a a n2n1 n2n2 2n1 n 2n1 2n 1 1 1 1  1 1 3 1 3 ∴T n b 1 b 2 b n 1 2     1 2    2  3    n1  n      2  2n  2 , 3 综上,知T  . n 2 16．（2024云南省昆明市五华区高三上学期第五次检测数学试题）已知数列 满足 , 数列 满足 ． (1)求 , 的值及数列 的通项公式； (2)若 （ , ）,求 的取值范围； (3)在数列 中,是否存在正整数 , ,使 , , （ , , ）构成等比数列？若存在,求符合条 学科网（北京）股份有限公司件的一组 的值,若不存在,请说明理由． 【解析】（1）由已知得： , ． 因为 , ,所以 , 而 ,所以 是以1为首项,2为公差的等差数列, 所以数列 的通项公式为 ． （2）不等式 化为： , 设 , 则 , 所以 在 上单调递增, 所以 ,因为 在 上恒成立, 所以 , 所以 的取值范围为 ． （3）若 , , （ , , ）构成等比数列, 则 ,即： , 学科网（北京）股份有限公司所以 , 由于 , 均为正整数,所以奇数 必须是完全平方数, 又因为 ,所以 , 则 为奇数的平方,不妨取 , , 所以,当 时, , ,即： ,不满足题意,舍去； 当 时, , ,即： , ,不满足题意,舍去； 当 时, , ,即： , . 所以符合条件的一组 的值可以是 ． 学科网（北京）股份有限公司