文档内容
宜宾市三中教育集团高2023级高二下三月月考
数学试题
一、单选题(本题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一个选项是符合
题目要求的.)
s(t)=3t3 −5t2
1.已知某质点的位移函数为 ,则当 时,该质点的瞬时速度是( )
A.−4m/s B.8m/s C. 68m/s D. 104m/s
2.函数 的单调递减区间为( )
(−∞,0] [−1,1]
A. B. C. D.
3.从7本不同的书中选出3本送给3位同学,每人一本,不同的选法种数是( )
A.21 B.210 C. D.
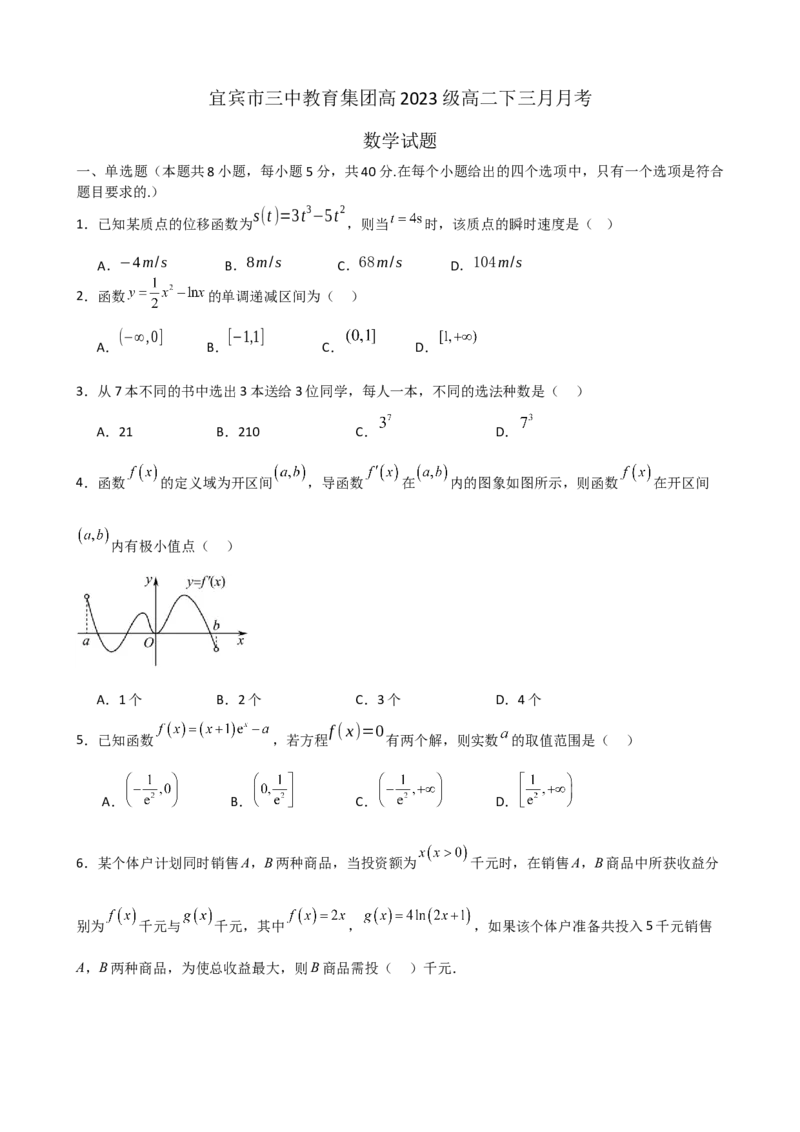
4.函数 的定义域为开区间 ,导函数 在 内的图象如图所示,则函数 在开区间
内有极小值点( )
A.1个 B.2个 C.3个 D.4个
f(x)=0
5.已知函数 ,若方程 有两个解,则实数 的取值范围是( )
A. B. C. D.
6.某个体户计划同时销售A,B两种商品,当投资额为 千元时,在销售A,B商品中所获收益分
别为 千元与 千元,其中 , ,如果该个体户准备共投入5千元销售
A,B两种商品,为使总收益最大,则B商品需投( )千元.A. B. C. D.
y=ln(2x) y=−ln(−2x)
7.已知直线 既是曲线 的切线,也是曲线 的切线,则( )
A. , B. ,
2 2
C.
k=
, D.
k=
,
e e
8.已知 是自然对数的底数, ,则( )
A. B. C. D.
二、多选题(本题共3小题,共18分,在每个小题给出的选项中,有多个选项是符合题目要求的.全部选
对的得6分,部分选对得部分分,有选错的得0分.)
9.下列命题正确的有( )
f(1)−f(1+Δx)
A.已知函数 在 上可导,若 ,则 lim =2
Δx
Δx→0
(
cosx) ' −xsinx−cosx
=
B. x x2
C. 在R上是增函数
D. 在 处的切线斜率是
''
f (x)
10.定义:设 是 的导函数, 是函数 的导数,若方程 有实数解 ,则称点
为函数 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”且“拐点”就是三
f(x)=ax3 +bx2 +c
次函数图象的对称中心.已知三次函数 的对称中心为 ,则下列说法中正确的有
( )
5
c=
A.若 3,则 ,
B.函数 既有极大值又有极小值
C.若 是 的极大值点,则 在区间 单调递增a>0 c∈(2,+∞)
D.当 时,函数 有三个零点时
11、已知函数 ,若 有两个极值点 ,则下面判断正确的有( )
A. B. C. D.
三、填空题(本题共3小题,每小题5分,共15分.)
3
f(x)= x2 −4ax+a2lnx
12、已知函数 2 在x=1处有极大值,则a=
13、若从0,1,2,3,4,5这六个数字中选3个数字,组成没有重复数字的三位偶数,则这样的三位数
一共有 个
14、已知定义在 上的连续奇函数 的导函数为 ,当 时, ,且
1 1 −3
f( )=−3,则不等式f(x− )< 的解集为
2 2 2x−1
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.)
f(x)=x−2sinx+1
15、已知函数
(0,f(0))
(1)求曲线 在点 处的切线方程;
[ π]
0,
(2)求函数 在区间 2 上的最大值与最小值.
16.已知函数 在 处的切线与直线
x+4 y=0
垂直
(1)求a的值;(2)求 的单调区间和极值.
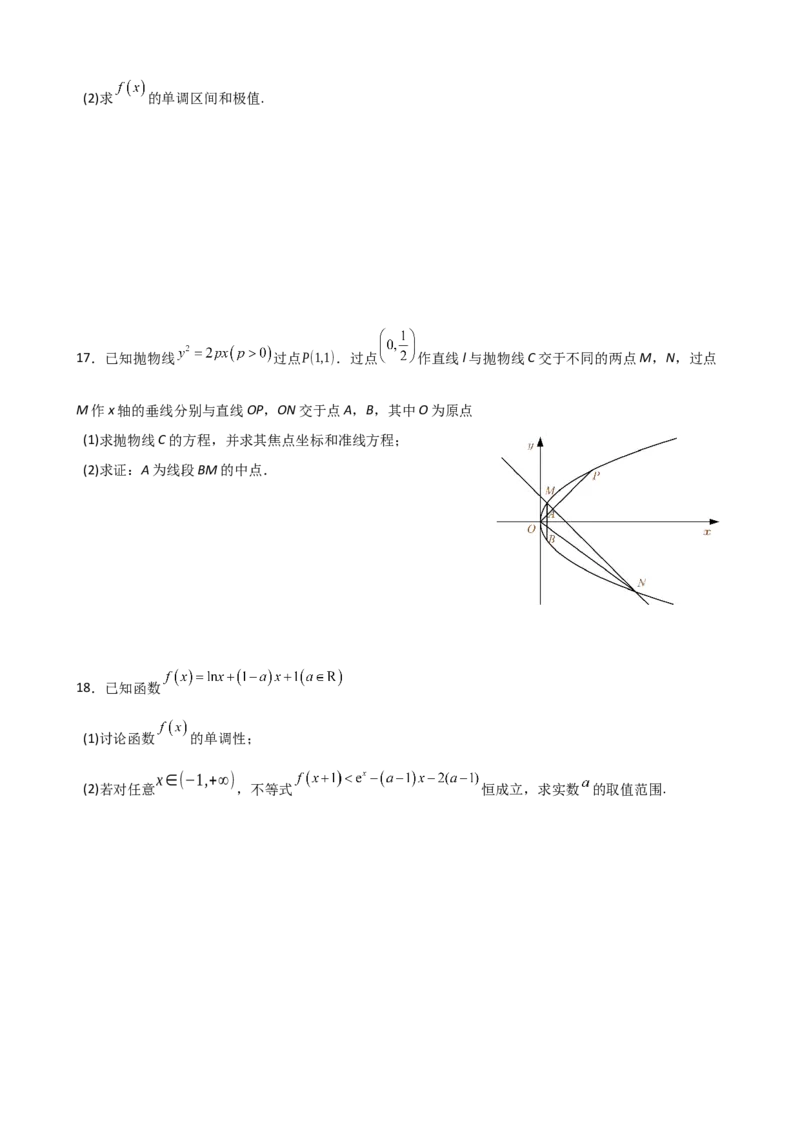
17.已知抛物线 过点P(1,1).过点 作直线l与抛物线C交于不同的两点M,N,过点
M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
18.已知函数
(1)讨论函数 的单调性;
x∈(−1,+∞)
(2)若对任意 ,不等式 恒成立,求实数 的取值范围.lnx+1
f(x)= +ax,(a∈R)
19.已知函数 x
(1)当 时,证明: ;
(0,1]
(2)若 在区间 单调递增,求实数 的取值范围;
(3)若 且 , ,证明:x2 +x2 >2.
1 2宜宾市三中教育集团高2023级高二下三月月考
数学试题答案
单选:DCBA ABCA
多选:BCD ABD ACD
( 1)
填空:3 52 0, ∪(1,+∞)
2
11、解:由题意知: 定义域为 , ;
当 时, , 有且仅有一个极值点 ,不合题意;
当 时,令 ,则 ;
由题意 ,且 所以 ,
对于A, 是方程 的两根, ,A正确;
对于B, , ,
, ;
, ,
,B错误;
对于C,当 时, , 当 时, 单调递减,
,C正确;
对于D, ,
是方程 的两根, , ,,
令 , ,
在 上单调递增, , ,D正确.
故选:ABD.
四、解答题
f' (x)=1−2cosx f' (0)=1−2cos0=−1
15、解:(1)由题意 ,
∵f(0)=1 (0,f(0)) y−1=−1(x−0)
又 ,所以曲线 在点 处的切线方程为 ,
y=−x+1
即 .......................................................................................................................................6分
[ π]
f' (x)=1−2cosx,x∈ 0,
(2)由题意 2
π π π
≤x≤ 0≤x≤
由f' (x)≥0,3 2 ,又由f' (x)≤0, 3
π π
[ π] [π π]
0, , ∵f( )= −1,f(0)=1
则f (x)在 3 递减, 3 2 递增. 2 2
π π
∴f (x) =f ( )= +1−√3
min 3 3 , f (x) max =f (0)=1
............................................................................................................................13分
16.解:(1)由题意知 ,
x+4 y=0
所以 ,又函数 在点 处的切线与直线 垂直,
所以 ,解得 ,即a的值为1....................................................................7分
(3)由(1)知 , ,令 ,解得 或 ,
所以当 或 时, ,当 时, ,
所以 的单调递增区间为 、 ,单调递减区间为 ,
又 , ,所以 的极大值为 ,极小值为 ..................................15分
17.解:(1)由抛物线C: 过点P(1,1),得 .
所以抛物线C的方程为 . 抛物线C的焦点坐标为( ,0),准线方程为 .............6分
(2)由题意,设直线l的方程为 ( ),l与抛物线C的交点为 , .
由 ,得 ..........................................................................................8分
则 , .................................................................................................................9分
因为点P的坐标为(1,1),所以直线OP的方程为 ,点A的坐标为 .......................10分
y x
( )
x , 2 1
直线ON的方程为 ,点B的坐标为 1 x ................................................................12分
2
y x y x +y x −2x x
因为 y + 2 1 −2x = 1 2 2 1 1 2
1 x 1
2
, 所以 .
故A为线段BM的中点................................................................................................................15分
18.解:(1)因为 ,所以 ..........................................1分
因为 ,若 ,即 时, 在 上单调递增,..........................................4分
若 ,即 时,令 ,得 ;令 ,得 ,所以 在 上单调递增,在 上单调递减.
综上,当 时, 在 上单调递增;当 时, 在 上单调递增,在
上单调递减............................................................................................................................................8分
(2)因为 , 恒成立,
所以 ,则 ,.............................10分
令 且 ,则 ,
令 ,则 ,故 在 上单调递增,.............13分
又 ,所以 时, ; 时, ,
所以 在 上单调递减,在 上单调递增, ,.............................16分
所以 ,实数 的取值范围为 .........................................................................................17分
19.解:(1)由 ,,得 ,
当 时, , 单调递增,当 时, , 单调递减,
所以 ...................................................................................................................3分
−lnx lnx
f' (x)= +a≥0 ∴a≥
x2 (0,1] x2 (0,1]
(2)由题 在区间 上恒成立, 在区间 上恒成立.
lnx
h(x)= ,x∈(0,1]
x2
令 ,
1−2lnx lnx
h' (x)= >0在x∈(0,1] ∴h(x)= 在(0,1]
x3 x2
上恒成立, 递增
∴h(x)
max
=0
,
∴a≥0
.......................................................................................................................6分(3)由 可得 ,两边取对数并整理,
得 ,即 ,...........................................................................8分
不妨设 ,由(1)知,函数 在 上单调递增,在 上单调递减, ,
而 ,且当 时, 恒成立,得到 ,.......................................................10分
记 , ,
则 ,
所以函数 在 上单调递增,....................................................................................................13分
所以 ,即 ,于是 ,
又 在 上单调递减,所以 .................................................................................15分
x2 +x2 >x2 +(2−x ) 2 =2x2 −4x +4=2(x −1) 2 +2>2
所 1 2 1 1 1 1 1 ,得证.............................................17分