文档内容
东北三省精准教学 2024 年 12 月高三联考 强化卷
数 学
本试卷满分 分,考试时间 分钟
150 120 .
一、选择题:本题共8小题,每小题5分,共40分。 在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数z满足 z z 则 z
1+i = -2i, | |=
. 3 . 5 . 10 . 5
A B C D
2 2 2 2
2.设集合A a a2 B a C a 则下列选项中一定成立的是
={-1, , -2}, ={0,2, +2}, ={- },
.A C A .A C .B C B .A B
A ∪ = B ∩ =⌀ C ∪ = D ∩ =⌀
r
3.已知一圆台内切球G与圆台各个面均相切 记圆台上 下底面半径分别为r r 若 1 1 则圆台的体积与球
, 、 1, 2, r = ,
2 3
的体积之比为
.13 . 3 . .19
A B C 2 D
6 2 12
4.在 ABC中 角A B C所对的边分别为a b c 若C π b b A a B 则B的大小为
△ , , , , , , = , + cos = cos ,
3
. π . π . π .2π
A B C D
6 3 9 9
{ax - a x a
5.已知a 且a 若函数f x , ≤ , 的值域为R 则a的取值范围是
>0 ≠1, ( )= x a x a ,
loga( + )+1, >
( ù é )
. 1 ú ú . ê ê 1 . .
A 0, û B ë ,1 C (1,2] D [2,+∞)
2 2
6.已知定义在R上的函数f x 满足 f x f x x 则曲线y f x 在点 f 处的切线方程为
( ) 2 ( )= (- )+3e , = ( ) (0, (0))
.y x .y x .y x .y x
A =3 +3 B =3 -3 C = +3 D = -3
S
7.在等比数列 a 中 S 为其前n项和 a 且 a a a 成等差数列 则 n n N∗ 的最小值为
{ n} , n , 1=1, 4 1,2 2, 3 , n( ∈ )
. 1 . 4 .16 .
A B C D 1
2 9 25
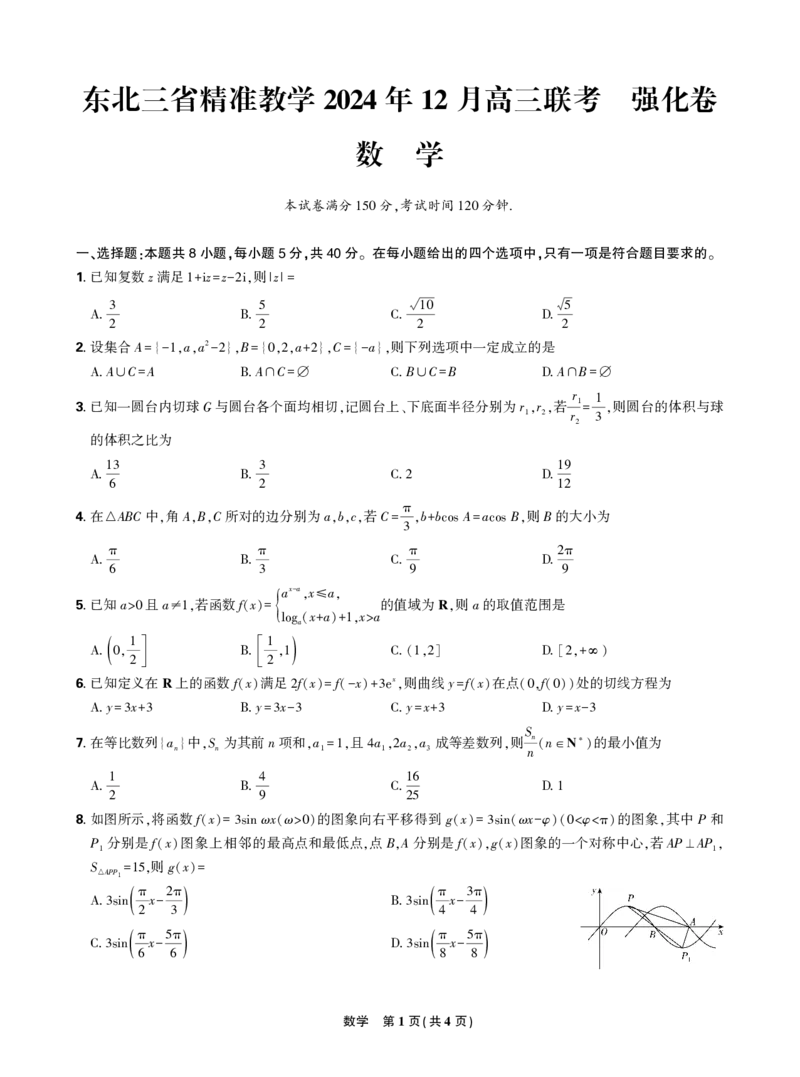
8.如图所示 将函数f x ωx ω 的图象向右平移得到 g x ωx φ φ 的图象 其中 P 和
, ( )= 3sin ( >0) ( )= 3sin( - )(0< <π) ,
P 分别是f x 图象上相邻的最高点和最低点 点B A 分别是f x g x 图象的一个对称中心 若AP AP
1 ( ) , , ( ), ( ) , ⊥ 1,
S 则g x
△ APP 1 =15, ( )=
( ) ( )
. πx 2π . πx 3π
A 3sin - B 3sin -
2 3 4 4
( ) ( )
. πx 5π . πx 5π
C 3sin - D 3sin -
6 6 8 8
数学 第1页(共4页)
{#{QQABJYQAgggoAAAAAQgCQwGACAOQkhCCAagOxBAEsAAASANABAA=}#}二、选择题:本题共3小题,每小题6分,共18分。 在每小题给出的选项中,有多项符合题目要求。 全部选对的
得6分,部分选对的得部分分,有选错的得0分。
9.已知方程Ax2 By2 Cxy Dx Ey F 其中A B C D E F.下列命题为真命题的是
+ + + + + =0, ≥ ≥ ≥ ≥ ≥
.可以是圆的方程 .可以是抛物线的方程
A B
.可以是椭圆的标准方程 .可以是双曲线的标准方程
C D
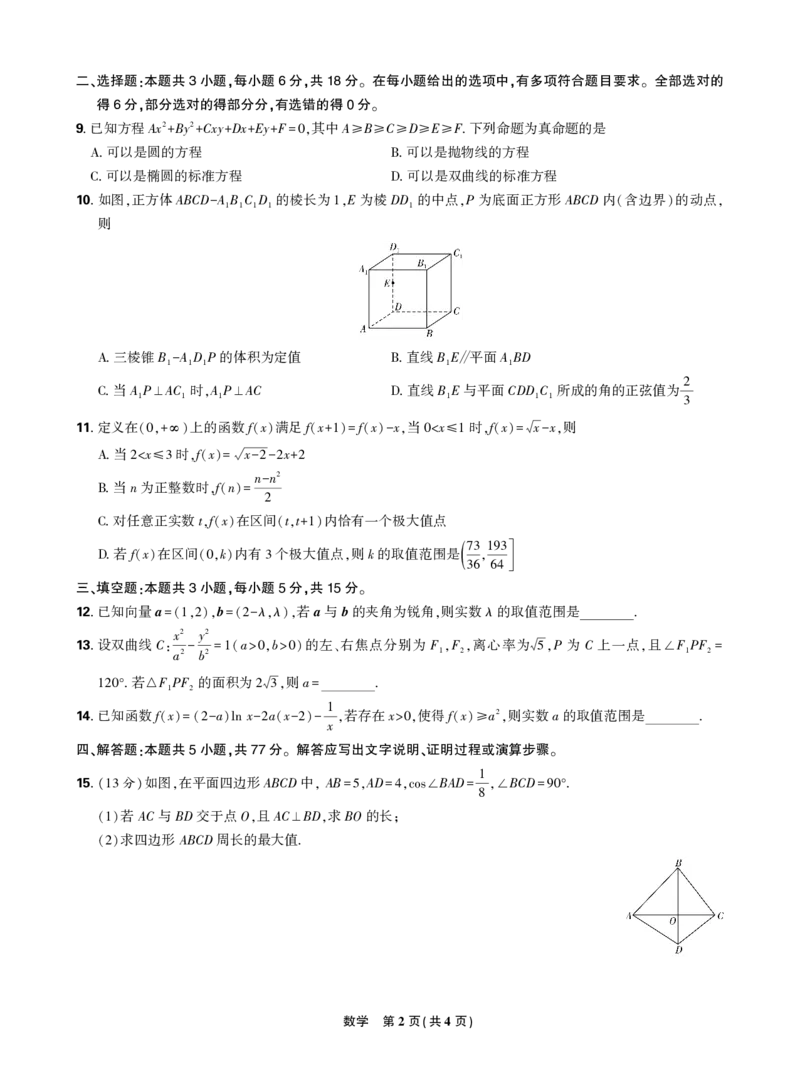
10.如图 正方体ABCD A B C D 的棱长为 E为棱DD 的中点 P 为底面正方形 ABCD 内 含边界 的动点
, - 1 1 1 1 1, 1 , ( ) ,
则
.三棱锥B A D P的体积为定值 .直线B E 平面A BD
A 1- 1 1 B 1 ∥ 1
.当A P AC 时 A P AC .直线B E与平面CDD C 所成的角的正弦值为2
C 1 ⊥ 1 , 1 ⊥ D 1 1 1
3
11.定义在 上的函数f x 满足f x f x x 当 x 时 f x x x 则
(0,+∞) ( ) ( +1)= ( )- , 0< ≤1 , ( )= - ,
.当 x 时 f x x x
A 2< ≤3 , ( )= -2-2 +2
n n2
.当n为正整数时 f n -
B , ( )=
2
.对任意正实数t f x 在区间 t t 内恰有一个极大值点
C , ( ) ( , +1)
( ù
.若f x 在区间 k 内有 个极大值点 则k的取值范围是 73 193ú ú
D ( ) (0, ) 3 , , û
36 64
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量a b λ λ 若a与b的夹角为锐角 则实数λ的取值范围是 .
=(1,2), =(2- , ), ,
x2 y2
13.设双曲线 C a b 的左 右焦点分别为 F F 离心率为 P 为 C 上一点 且 F PF
:a2 -b2 =1( >0, >0) 、 1, 2, 5, , ∠ 1 2=
°.若 F PF 的面积为 则a .
120 △ 1 2 2 3, =
14.已知函数f x a x a x 1 若存在x 使得f x a2 则实数a的取值范围是 .
( )=(2- )ln -2 ( -2)- x , >0, ( )≥ ,
四、解答题:本题共5小题,共77分。 解答应写出文字说明、证明过程或演算步骤。
15.( 分)如图 在平面四边形ABCD中 AB AD BAD 1 BCD °.
13 , , =5, =4,cos∠ = ,∠ =90
8
若 AC与BD交于点O 且AC BD 求BO的长
(1) , ⊥ , ;
求四边形 ABCD周长的最大值.
(2)
数学 第2页(共4页)
{#{QQABJYQAgggoAAAAAQgCQwGACAOQkhCCAagOxBAEsAAASANABAA=}#}16.( 分)已知四棱柱ABCD A B C D 如图所示 底面ABCD为平行四边形 其中点D在平面A B C D 内的
15 - 1 1 1 1, , , 1 1 1 1
投影为点A 且AB AA AD ABC °.
1, = 1=2 ,∠ =120
求证 平面A BD 平面ADD A
(1) : 1 ⊥ 1 1;
DE
已知点 E 在线段 C D 上 不含端点位置 且平面 A BE 与平面 BCC B 的夹角的余弦值为 5 求
(2) 1 ( ), 1 1 1 , EC
5 1
的值.
( ) ( )
17.( 分)已知函数f x π x x π .
15 ( )=sin +4 +sin 4 -
3 6
é ù
求f x 在ê ê πú ú上的单调递增区间.
(1) ( ) ë0, û
2
( x ) ( x )
若关于x的方程 f π f 5π a在区间 内有两个不同的解x x x x 求实数a
(2) 2 - + - = 2 [0,2π) 1, 2( 1< 2),
4 48 48 4
的取值范围 并证明 x x 2a2 .
, cos( 1- 2)= -1
5
数学 第3页(共4页)
{#{QQABJYQAgggoAAAAAQgCQwGACAOQkhCCAagOxBAEsAAASANABAA=}#}18.( 分)已知函数f x a ax a .
17 ( )= e ( ≠0)
若a 曲线y f x 在点 f 处的切线与直线x y 垂直 证明 f x x .
(1) >0, = ( ) (0, (0)) + -2=0 , : ( )>ln( +2)
ax ax
1 2
若对任意的x x 且x x 函数g x f x e -e 证明 函数g x 在 x x 上存在唯一零点.
(2) 1, 2 1< 2, ( )= ( )- x x , : ( ) ( 1, 2)
1- 2
19.( 分)定义 从数列 a 中随机抽取 m 项按照项数从小到大的顺序依次记为 a a a k k
17 : { n} k
1
, k
2
,…, km( 1< 2<…<
k 将它们组成一个项数为m的新数列 b 其中 b a i m 若数列 b 为递增数列 则称数
m), { n}, i= ki( =1,2,…, ), { n} ,
列 b 是数列 a 的 m项递增衍生列 .
{ n} { n} “ ”
{n n
, =1,3,5,
已知数列 a 满足 a 数列 b 是 a 的 项递增衍生列 写出所有满足条件的
(1) { n} n= n { n} { n} “3 ”,
4-2 n
2 , =2,4,6,
b ﹔
{ n}
已知数列 a 是项数为m 的等比数列 其中 m 若数列 b 为 求证 数列 b 不是数列
(2) { n} , ≥3, { n} 1,16,81, : { n}
a 的 项递增衍生列
{ n} “3 ”;
14
已知首项为 的等差数列 a 的项数为 且 a 数列 b 是数列 a 的 m项递增衍生列
(3) 1 { n} 14, ∑i= i=105, { n} { n} “ ”,
1
其中 m .若在数列 b 中任意抽取 项 且均不构成等差数列 求m的最大值.
1≤ ≤14 { n} 3 , ,
数学 第4页(共4页)
{#{QQABJYQAgggoAAAAAQgCQwGACAOQkhCCAagOxBAEsAAASANABAA=}#}