文档内容
2024-2025 学年第一学期高三七诊考试(数学试卷)
考试时间:120分钟; 试卷分值:150分 命题人:薛梅
一、单选题(共8小题,每小题5分)
1. 集合 ,集合 ,则 ( )
A. B. C. D.
2. 已知复数 满足 ,则 ( )
A. B. C. D.
3. 已知直线l经过点 ,且与直线 垂直,则直线l的方程为( )
A. B. C. D.
4. 设S 为等差数列{a}的前n项和,且 ,则S =( )
n n 13
A. 78 B. 91 C. 39 D. 26
5. 若 、 且 ,则下列不等式中正确的是( )
A. B. C. D.
6. 若向量 的夹角为 , ,若 ,则实数 ( )
A. B. C. D.
7. 已知函数 ,则( )
A. 它的最小值为 B. 它的最大值为2
C. 它的图象关于直线 对称 D. 它的图象关于点 对称
第1页/共5页
学科网(北京)股份有限公司8. 设椭圆 ( )的左焦点为F,O为坐标原点.过点F且斜率为 的直线与C的
一个交点为Q(点Q在x轴上方),且 ,则C的离心率为( )
A. B. C. D.
二、多选题(共3小题,每小题6分)
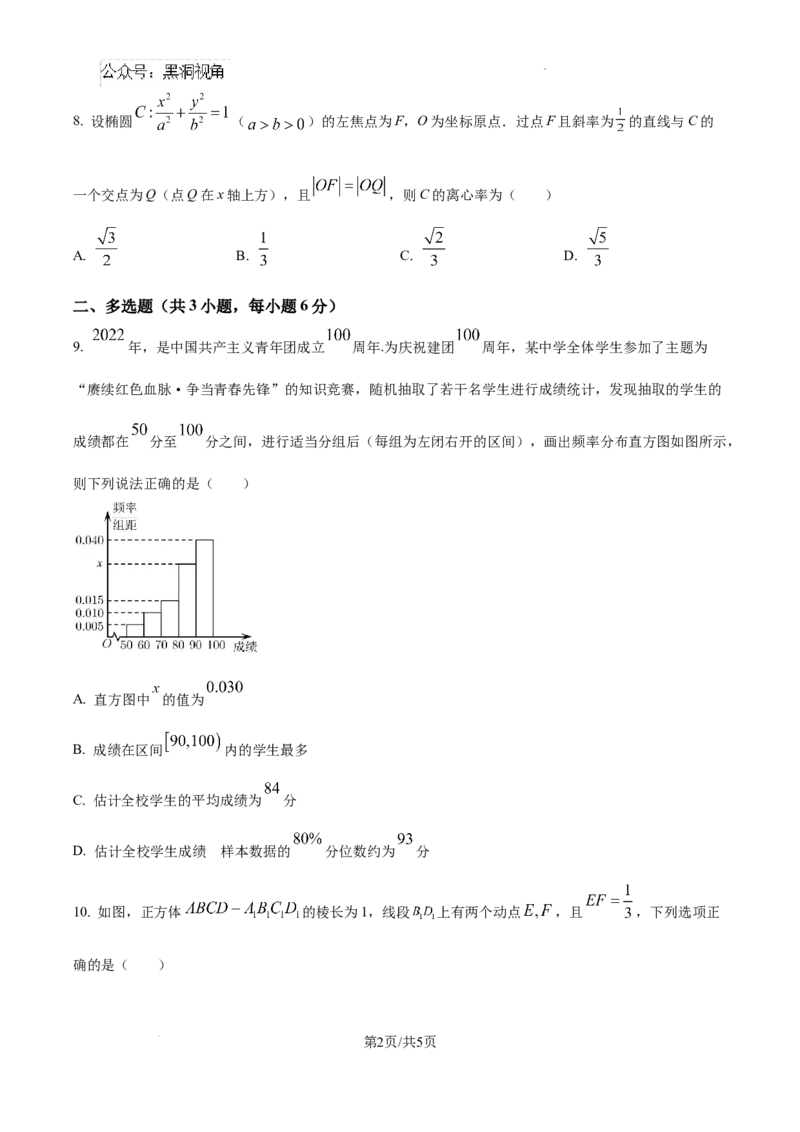
9. 年,是中国共产主义青年团成立 周年.为庆祝建团 周年,某中学全体学生参加了主题为
“赓续红色血脉·争当青春先锋”的知识竞赛,随机抽取了若干名学生进行成绩统计,发现抽取的学生的
成绩都在 分至 分之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示,
则下列说法正确的是( )
A. 直方图中 的值为
B. 成绩在区间 内的学生最多
C. 估计全校学生的平均成绩为 分
的
D. 估计全校学生成绩 样本数据的 分位数约为 分
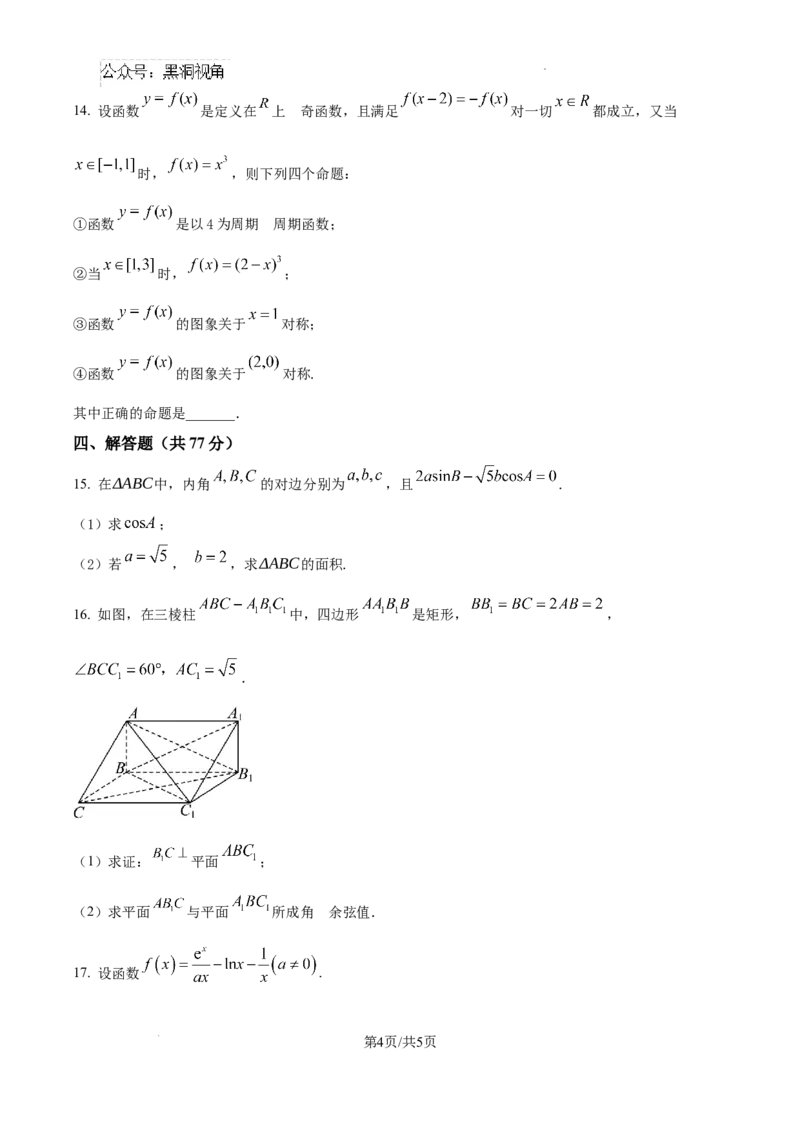
10. 如图,正方体 的棱长为1,线段 上有两个动点 ,且 ,下列选项正
确的是( )
第2页/共5页
学科网(北京)股份有限公司A.
.
B 平面
C. 的面积与 的面积相等
D. 三棱锥 的体积为定值
11. 抛物线 的焦点为 、 为其上一动点,当 运动到 时, ,直线 与抛物线
相交于 、 两点,点 ,下列结论正确的是( )
A. 抛物线的方程为
B. 的最小值为4
C. 当直线 过焦点 时,以 为直径的圆与 轴相切
D. 存在直线 ,使得 两点关于 对称
三、填空题(共3小题,每小题5分)
12. 记 为递增等比数列 的前 项和,若 , ,则 ___.
13. 为了落实立德树人的根本任务,践行五育并举,某校开设 三门德育校本课程,现有甲、乙、丙、
丁四位同学参加校本课程的学习,每位同学仅报一门,每门至少有一位同学参加,则不同的报名方法有
_____________.
第3页/共5页
学科网(北京)股份有限公司的
14. 设函数 是定义在 上 奇函数,且满足 对一切 都成立,又当
时, ,则下列四个命题:
的
①函数 是以4为周期 周期函数;
②当 时, ;
③函数 的图象关于 对称;
④函数 的图象关于 对称.
其中正确的命题是_______.
四、解答题(共77分)
15. 在ΔABC中,内角 的对边分别为 ,且 .
(1)求 ;
(2)若 , ,求ΔABC的面积.
16. 如图,在三棱柱 中,四边形 是矩形, ,
.
(1)求证: 平面 ;
的
(2)求平面 与平面 所成角 余弦值.
17. 设函数 .
第4页/共5页
学科网(北京)股份有限公司(1) 时,求曲线 在点 处的切线方程;
(2)证明: 至多只有一个零点.
18. 已知椭圆 过点 ,且离心率 .
(1)求椭圆C的标准方程;
(2)若直线 与椭圆C相交于 两点( 不是左右顶点),椭圆的右顶点为D,且满足
,试判断直线l是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
19. 已知数列 的前 项和为 ,点 在函数 图象上;
(1)证明 是等差数列;
(2)若函数 ,数列 满足 ,记 ,求数列 前 项和 ;
(3)是否存在实数 ,使得当 时, 对任意 恒成立?若存在,求
出最大的实数 ,若不存在,说明理由.
第5页/共5页
学科网(北京)股份有限公司