文档内容
2024-2025 学年山东省东营市高二上学期期末质量监测数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1. ( )
C7 C10−C0 =
10 10 10
A. 119 B. 120 C. 1199 D. 1200
2.已知直线l 的斜率为−1,直线l 的倾斜角比直线l 的倾斜角小30∘,则直线l 的斜率为( )
1 2 1 2
−2+√3 −2−√3
A. −2+√3 B. −2−√3 C. D.
2 2
3.平面α的斜线AB交平面α于点B,过定点A的动直线l与直线AB垂直,且交平面α于点C,那么动点C的
轨迹是( )
A. 线段 B. 直线 C. 圆 D. 抛物线
4.已知 P(1,2) 是直线 l 上一点,⃗ v=(3,−4) 是直线 l 的一个法向量,则直线 l 的方程为( )
A. 4x+3 y+5=0 B. 4x−3 y+5=0 C. 3x−4 y+5=0 D. 3x+4 y+5=0
5.如图,已知A,B,C是边长为1的小正方形网格上不共线的三个格点,点P为平面ABC外一点,且
⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗
==120∘,|AP|=3 ,若 AO=AB+AC ,则|OP|=( )
A. 2√10 B. √37 C. 6 D. √35
6.已知 ,则 ( )
(x2−x−1) 5=a +a (x−1)+a (x−1) 2+⋯+a (x−1) 10 a +a +⋯+a =
0 1 2 10 1 2 10
A. 1 B. 2 C. 3 D. 5
7.已知三棱柱 的底面是边长为 的正三角形,侧棱 底面 ,且 ,则异
ABC−A B C 2 A A ⊥ ABC A A =√2
1 1 1 1 1
面直线A B,AC 所成角的大小为( )
1 1
π π π π
A. B. C. D.
6 4 3 2
第 页,共 页
1 18.若直线 与椭圆 x2 y2 交于 , 两点,点 满足 ,
x+3 y−2m=0 C: + =1(a>b>0) A B P(m,0) |PA|=|PB|
a2 b2
则椭圆C的离心率为( )
√109 √110 √111 4√7
A. B. C. D.
11 11 11 11
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A. 若m,n⊂α,m//β,n//β,则α//β
B. 若α//β,m⊥α,n//β,则m⊥n
C. 若m,n异面,m⊂α,m//β,n⊂β,n//α,则α//β
D. 若m⊥n,m//α,α//β,则n⊥β
10.将2个男生和5个女生排成一排,下列表述正确的有( )
A. 男生不在头尾的不同排法有2400种
B. 男生不在头尾且不相邻的不同排法有600种
C. 假设这7个学生身高均不相等,最高的人站在中间,从中间到左边和从中间到右边身高都递减,则不同
的排法有20种
D. 2个男生都不与女生甲相邻的不同排法有24000种
11.已知O为坐标原点,动点P到x轴的距离为d,且|OP|2=λ+μd2,其中λ,μ均为常数,动点P的轨迹
称为(λ,μ)曲线,则下列说法正确的是( )
A. (λ,μ)曲线一定都关于坐标轴对称
B. (7,2)曲线的离心率为2
1
C. 若( ,μ)曲线为焦点在y轴上的椭圆,则μ的取值范围是(0,1)
2
D. 设曲线Ω为(2,−1)曲线,曲线Ω与x轴交于A,B两个不同的点,M ,M ,M ,M ,M 是线段AB
1 2 3 4 5
的6等分点,分别过这五个点作斜率为k(k≠0)的一组平行线,交曲线Ω于点P ,P ,⋯,P ,则AP ,
1 2 10 1
1
AP ,⋯,AP 这10条直线的斜率的乘积为−
2 10 32
三、填空题:本题共3小题,每小题5分,共15分。
1
12.(1+2x2 )(x+ ) 4的展开式中常数项为 .(用数字作答)
x
第 页,共 页
2 113.已知直线x−y+1=0与圆C:x2+ y2−4x−2y+m=0交于A,B两点,|AB|=2√2,则过点P(4,4)
的圆C的切线长为 .
14.已知平面ABC⊥平面α,线段AB在平面α内,D为线段AB的中点,|AB|=2√2,∠CDB=45∘,点
P为α内的动点,且点P到直线CD的距离为√2,则动点P的轨迹Γ的离心率为 ,如果CD=√2,在平
面α内过点B的直线与Γ交于M,N两点,则三棱锥C−AMN的体积的最大值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
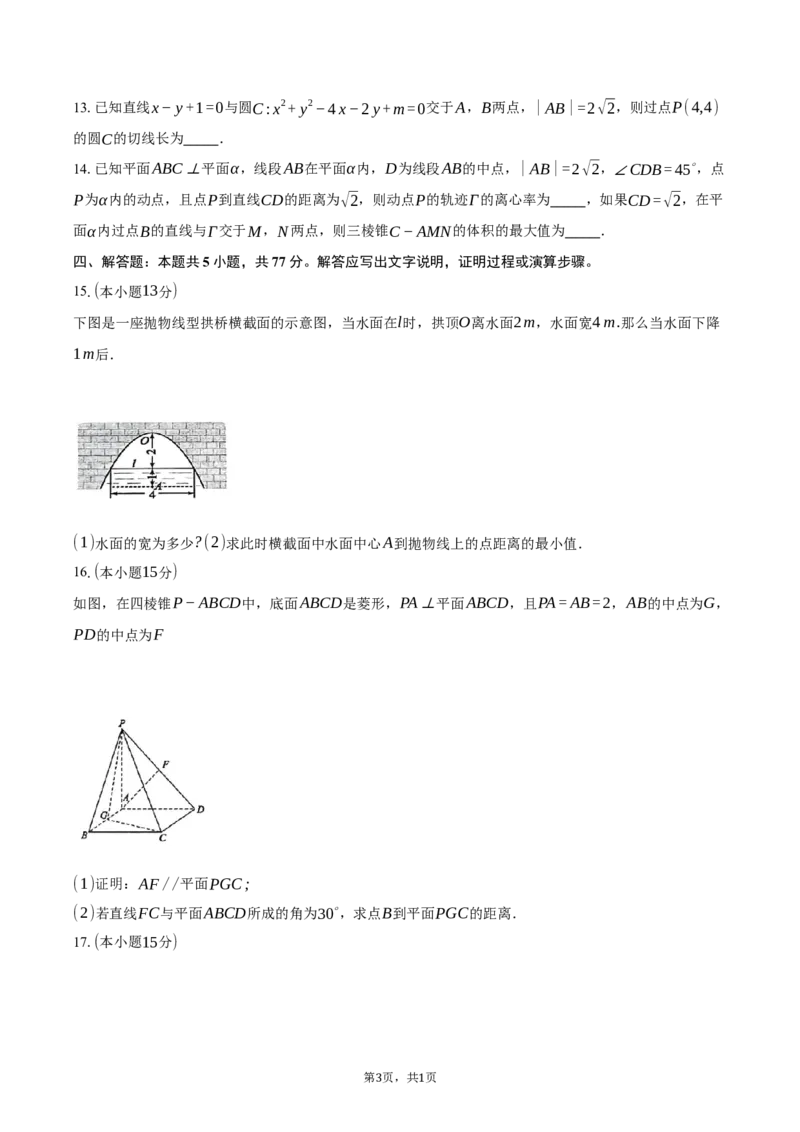
15.(本小题13分)
下图是一座抛物线型拱桥横截面的示意图,当水面在l时,拱顶O离水面2m,水面宽4m.那么当水面下降
1m后.
(1)水面的宽为多少?(2)求此时横截面中水面中心A到抛物线上的点距离的最小值.
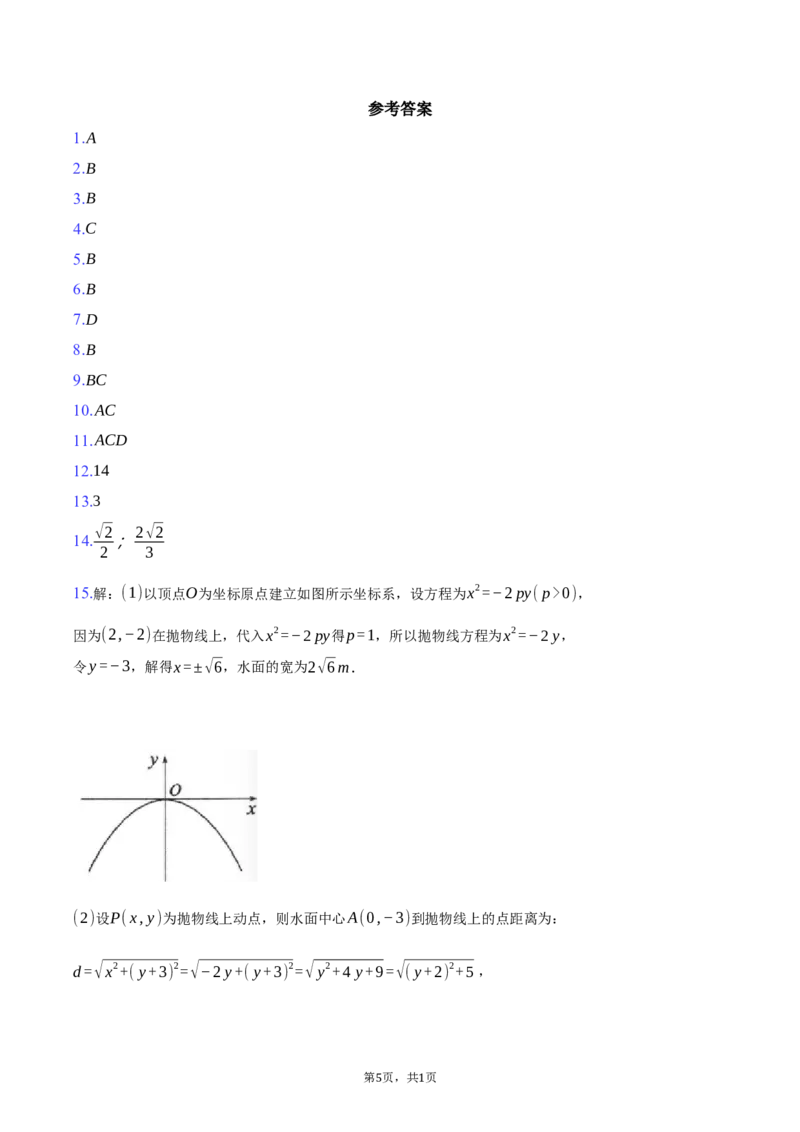
16.(本小题15分)
如图,在四棱锥P−ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,AB的中点为G,
PD的中点为F
(1)证明:AF//平面PGC;
(2)若直线FC与平面ABCD所成的角为30∘,求点B到平面PGC的距离.
17.(本小题15分)
第 页,共 页
3 1已知双曲线
x2 y2
的左、右焦点分别为 , ,且 ,点 在双
C: − =1(a>0,b>0) F F |F F |=2√5 (√2,2)
a2 b2 1 2 1 2
曲线C上.
(1)求双曲线C的方程;
(2)设双曲线C的左右顶点分别为A,B,过点T(2,0)的直线l交双曲线C于点M,N(M在第一象限),记
直线 , 的斜率分别为 , ,判断k 是否是定值,若是定值,请求出此定值 若不是定值,请说明
AM BN k k 1 ;
1 2 k
2
理由.
18.(本小题17分)
如图,在四棱锥P−ABCD中,平面PAB⊥平面ABCD,AB⊥AD,AD//BC,PA=BC=3,
AB=AD=2,PB=√13,E为PD中点,点F在PC上,且PC=3FC.
(1)求证:AB⊥平面PAD;
(2)求二面角F−AE−D的余弦值;
(3)线段AC上是否存在点Q,使得DQ//平面FAE?若存在,求线段AQ的长;若不存在,说明理由.
19.(本小题17分)
已知椭圆 x2 y2 的离心率为√2,直线 与椭圆 交于 , 两点.
C: + =1(a>b>0) y=kx(k>0) C A B
a2 b2 2
(1)若点P为椭圆C上异于点A,B的点.
①若直线AP,BP斜率分别为k ,k ,求证:k k 为定值;
1 2 1 2
②若直线AP⊥AB,点A在x轴上的射影为点D,求证:B,P,D三点共线.
(2)设A在第一象限,点M为椭圆C的上顶点,点M关于直线x−y=0的对称点为点N,直线AB与直线
|AQ| √6−√2
MN交于点Q,且 = ,求直线AB的方程.
|NQ| 2sin∠NOQ
第 页,共 页
4 1参考答案
1.A
2.B
3.B
4.C
5.B
6.B
7.D
8.B
9.BC
10.AC
11.ACD
12.14
13.3
√2 2√2
14. ;
2 3
15.解:(1)以顶点O为坐标原点建立如图所示坐标系,设方程为x2=−2py(p>0),
因为(2,−2)在抛物线上,代入x2=−2py得p=1,所以抛物线方程为x2=−2y,
令y=−3,解得x=±√6,水面的宽为2√6m.
(2)设P(x,y)为抛物线上动点,则水面中心A(0,−3)到抛物线上的点距离为:
d=√x2+(y+3) 2=√−2y+(y+3) 2=√y2+4 y+9=√(y+2) 2+5 ,
第 页,共 页
5 1所以d =√5.
min
故此时水面中心到抛物线上的点距离的最小值为√5m
1
16.(1)证明:设PC的中点为H,连结FH,HG.因为FH//CD,FH= CD,AG//CD,
2
1
AG= CD,
2
所以FH//AG,FH=AG,所以四边形AGHF为平行四边形,
则AF//GH,又GH⊂平面PGC,AF⊄平面PGC,所以AF//平面PGC.
(2)因为PA⊥平面ABCD,取AD的中点M,连结FM,CM,
则FM//PA,FM=1,所以FM⊥平面ABCD,
π
所以∠FCM为FC与平面ABCD所成的角,故∠FCM= ,在RtΔFCM中,CM=√3,
6
π
在△DCM中,CD=2,DM=1,所以CM2+DM2=CD2,所以CM⊥AD.所以∠CDM= .
3
因为PA⊥平面ABCD,CG⊂平面ABCD.所以PA⊥CG,
又因为CG⊥AB,PA、AB⊂平面PAB,PA∩AB=A,所以CG⊥平面PAB.
又因为PG⊂平面PAB,所以CG⊥PG.
√15
在在RtΔPCG中,CG=√3,PG=√5,所以S = .
△PCG 2
第 页,共 页
6 1√3
在在Rt△BCG中,CG=√3,BG=1,所以S = ,
△BCG 2
S |PA| 2√3 2√5
由V =V ,得点B到平面PGC的距离d= ΔBCG = = .
三棱锥B−PCG 三棱锥P−BCG S √15 5
ΔPCG
{a2+b2=5
17.解: 依题意, ,
(1) 2 4
− =1
a2 b2
解得a2=1,b2=4,
y2
故双曲线C的方程为x2− =1.
4
(2)设直线l的方程为x=my+2,M(x ,y ),N(x ,y ),
1 1 2 2
由{ x=my+2 整理得 ,
(4m2−1)y2+16my+12=0
4x2−y2=4
,
Δ=256m2−48(4m2−1)=64m2+48>0
16m 12
由韦达定理得:y + y =− ,y y = ,
1 2 4m2−1 1 2 4m2−1
3
得:m y y =− (y + y ),
1 2 4 1 2
由题 y , y ,
k = 1 k = 2
1 x +1 2 x −1
1 2
所以k y (x −1) y (my +1)
1= 1 2 = 1 2
k y (x +1) y (my +3)
2 2 1 2 1
第 页,共 页
7 13 1 3
− (y + y )+ y y − y
4 1 2 1 4 1 4 2 1
= = =− ,
3 3 9 3
− (y + y )+3 y − y + y
4 1 2 2 4 1 4 2
所以k 是定值,k 1.
1 1=−
k k 3
2 2
18.解:(1)在△PAB中,PA2+AB2=PB2,
π
所以∠PAB= ,即AB⊥PA,又因为AB⊥AD,
2
在平面PAD中,PA∩AD=A,PA、AD⊂平面PAD,
所以AB⊥平面PAD.
(2)因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AB⊥AD,AD⊂平面ABCD,
所以AD⊥平面PAB,又PA⊂平 面P,所A以B AD⊥PA,
由(1)已证AB⊥PA,且已知AB⊥AD,
故以A为原点,建立如图空间直角坐标系A−xyz,
则D(2,0,0),P(0,0,3),C(3,2,0).
⃗ ⃗ ⃗ ⃗
所以AP=(0,0,3) ,AD=(2,0,0) ,AC=(3,2,0) ,CP=(−3,−2,3) ,
因为E为PD中点,
第 页,共 页
8 1⃗ 1 ⃗ ⃗ 3
所以AE= (AD+AP)=(1,0, ),
2 2
⃗ ⃗ ⃗ ⃗ 1 ⃗ 4
由点F在PC上,且PC=3FC知,AF=AC+CF=AC+ CP=(2, ,1),
3 3
3
{⃗ ⃗ { x+ z=0
n·AE=0 2
设平面AEF的法向量为⃗n=(x,y,z),则 ,即 ,
⃗ ⃗ 4
n·AF=0 2x+ y+z=0
3
⃗
令z=2,则x=−3,y=3,于是n=(−3,3,2) ,
⃗
又因为由(1)已证AB⊥平面PAD,所以平面PAD的一个法向量为AB=(0,2,0) ,
⃗ ⃗
⃗ n·AB 3×2 3√22
⃗ ,AB⟩= = = ,
cos⟨n
⃗ ⃗ 2×√22 22
|n||AB|
3√22
由题知,二面角F−AE−D的平面角为锐角,所以其余弦值为 .
22
⃗ ⃗
(3)设Q是线段AC上一点,则存在λ∈[0,1]使得 AQ=λAC ,
⃗ ⃗
因为AC=(3,2,0) ,DA=(−2,0,0) ,
⃗ ⃗ ⃗ ⃗ ⃗
所以DQ=DA+AQ=DA+λAC=(3λ−2,2λ,0) ,
DQ⊄平面AEF,所以要使DQ//平面AEF,
当且仅当 D ⃗ Q· ⃗ n=0 ,即(3λ−2,2λ,0)·(−3,3,2)=0,
整理得:(3λ−2)×(−3)+6λ=0,解得λ=2,
因为λ=2∉[0,1],所以线段AC上不存在点Q,使得DQ//平面AEF.
第 页,共 页
9 1√2
19.解:(1)因为椭圆离心率为 ,所以a2=2b2.
2
设 ,则
,则x2 y2
,解得: .
A(x ,y ) B(−x ,−y ) 0+ 0=1 x2=2b2−2y2
0 0 0 0 a2 b2 0 0
设 ,则m2 n2 ,整理得 .
① P(m,n) + =1 m2=2b2−2n2
a2 b2
k k =
y
0
−n
×
−y
0
−n
=
y2
0
−n2
=
y2
0
−n2
=−
1.
1 2 x −m −x −m x2−m2 (2b2−2y2 )−(2b2−2n2 ) 2
0 0 0 0
依题意得: , y ,
② D(x ,0) k = 0
0 AB x
0
{k k =−1
AB 1 y y
因为 所以 ,即: .
1 k = 0 k = 0
k k =− 2 2x BP 2x
1 2 2 0 0
而 −y y ,
k = 0 = 0
BD −x −x 2x
0 0 0
所以k =k ,故B、P、D三点共线.
BP BD
b kb
(2)依题意得:MN方程为y=−x+b,与y=kx联立得:Q( , ).
k+1 k+1
|NQ| |OQ|
= =√2|OQ|
在△ONQ中,由正弦定理可得:sin∠NOQ π ,
sin
4
|AQ| √6−√2
又| = ,
|NQ| 2sin∠NOQ
所以|AQ|=(√3−1)|OQ|,即|OA|=√3|OQ|,
第 页,共 页
10 1√3b √3kb
所以A点的坐标为A( , ),
k+1 k+1
代入椭圆方程: 3b2 3k2b2 ,解得 1.
+ =1 k=
2b2 (k+1) 2 b2 (k+1) 2 2
1
故直线AB的方程为y= x
2
第 页,共 页
11 1