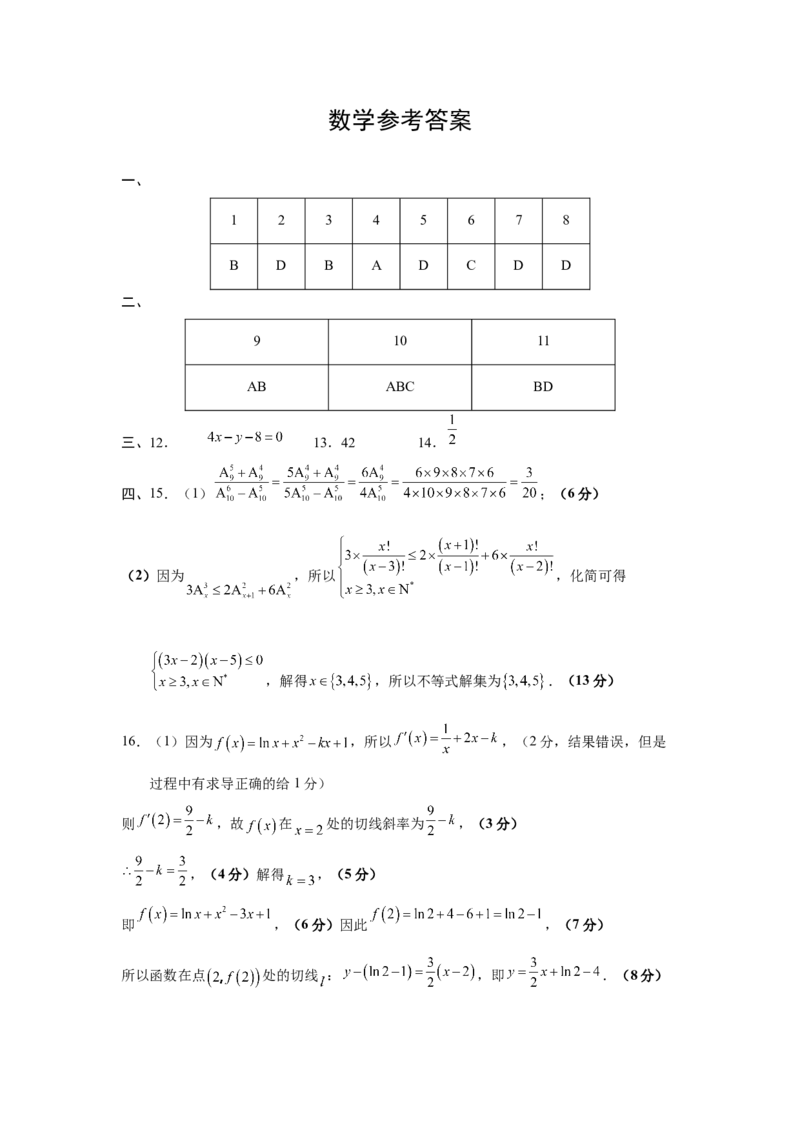文档内容
数学参考答案
一、
1 2 3 4 5 6 7 8
B D B A D C D D
二、
9 10 11
AB ABC BD
三、12. 13.42 14.
四、15.(1) ;(6分)
(2)因为 ,所以 ,化简可得
,解得 ,所以不等式解集为 .(13分)
16.(1)因为 ,所以 ,(2分,结果错误,但是
过程中有求导正确的给1分)
则 ,故 在 处的切线斜率为 ,(3分)
,(4分)解得 ,(5分)
即 ,(6分)因此 ,(7分)
所以函数在点 处的切线 : ,即 .(8分)(2)由(1)可得 ,定义域为 ,
又 ,(10分)
令 ,解得 或 ;令 ,解得 ,
所以 在 上单调递增,在 上单调递增,在 上单调递减,(12分)
则 在 处取得极大值,在 处取得极小值,(13分)
即极大值为 ,极小值为 ,
综上所述, 的单调递增区间为 和 ,单调递减区间为 ,极大值为
,极小值为 .(15分)
17.(1)由题意,先从余下的7人中选4人共有 种不同结果,(1分)
再将这4人与 进行全排列有 种不同的排法,(2分)
故由乘法原理可知共有 种不同排法.(3分)
(2)由题意,先从余下的6人中选3人共有 种不同结果,(4分)
再将这3人与 、 的进行全排列有 种不同的排法,(5分)
故由乘法原理可知共有 种不同排法,(6分)又 、 之间的排列有 ,
所以 排在 前面,有 种不同排法.(7分)
(3)因 , , 都在内,所以只需从余下5人中选2人有 种不同结果,(8分)
, 必须相邻,有 种不同排法,(9分)由于 与 , 都不相邻,先将选出的2人进行全排列共有 种不同排法,
再将 、 这个整体与 插入到选出的2人所产生的3个空位中有 种不同排法,(10
分)
由乘法原理可得共有 种不同排法.(11分)
(4)分四类:第一类:所选的5人无 、 ,共有 种排法;(12分)
第二类:所选的5人有 、无 ,共有 种排法;(13分)
第三类:所选的5人无 、有 ,共有 种排法;(14分)
第四类:所选的5人有 、 ,若A排中间时,有 种排法,
若 不排中间时,有 种排法,共有 种排法;
综上,共有 种不同排法.(15分)
18.(1)由题意知,w=(x-4)y=(x-4)(-x2+14x-36),
即w=-x3+18x2-92x+144(5≤x≤10,x∈N*).
(2)由(1)得,w′=-3x2+36x-92,
令w′=0,解得x =<5(舍去),x =∈(8,9),
1 2
所以当x∈[5,x )时,w′>0;当x∈(x ,10]时,w′<0,
2 2
所以w=-x3+18x2-92x+144在[5,x )上单调递增,在(x ,10]上单调递减,
2 2
又x∈N*,当x=8时,w=-512+1 152-736+144=48;
当x=9时,w=-729+1 458-828+144=45,所以当该款消毒液每件售价
为8元时,每日销售该款消毒液所获得的利润最大,日最大利润为48元.
19.(1)函数 的定义域为 ,
,(1分)
当 时,对任意的 , ,由 可得 ,由 可得 ,
此时,函数 的减区间为 ,增区间为 ;(2分)
当 时,由 可得 ,由 可得 或 ,
此时函数 的减区间为 ,增区间为 、 ;(3分)
当 时,对任意的 , ,此时函数 的增区间为 ;(4
分)当 时,由 可得 ,由 可得 或 ,
此时,函数 的减区间为 ,增区间为 、 .
综上所述,当 时,函数 的减区间为 ,增区间为 ;
当 时,函数 的减区间为 ,增区间为 、 ;
当 时, 的增区间为 ,无减区间;
当 时,函数 的减区间为 ,增区间为 、 .(5分,没有综上,只
要表达了单调区间不扣分)
(2)当 时, ,
即证 ,
令 ,即证 ,即证 ,(6分)
因为 ,(7分)
则函数 在 上单调递增,(8分)
当 时, ;当 时, ,所以函数 的值域为 ,(9分)
令 ,其中 ,则 ,
由 可得 ,由 可得 ,(10分)
所以函数 的减区间为 ,增区间为 ,则 ,
故 ,即 ,故原不等式得证.(11分)
(3) ,因为函数 有两个零点 、 ,不妨设
,则 ,(12分)所以, ,
整理可得 ,即 ,(13分)
要证 ,即证 ,即证 ,(14
分)
令 ,即证 ,令 ,其中 ,则
,(15分)所以函数 在 上为增函数,则
,(16分)即 ,即 ,故原不等式得证.(17
分)