文档内容
数 学 试 题
2025.03
(考试时间:120分钟 试卷满分:150分)
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.某物体沿直线运动,位移 单位: 与时间 单位: 之间的关系为 ,
该物体在 时的瞬时速度是( )
A. B. C. D.
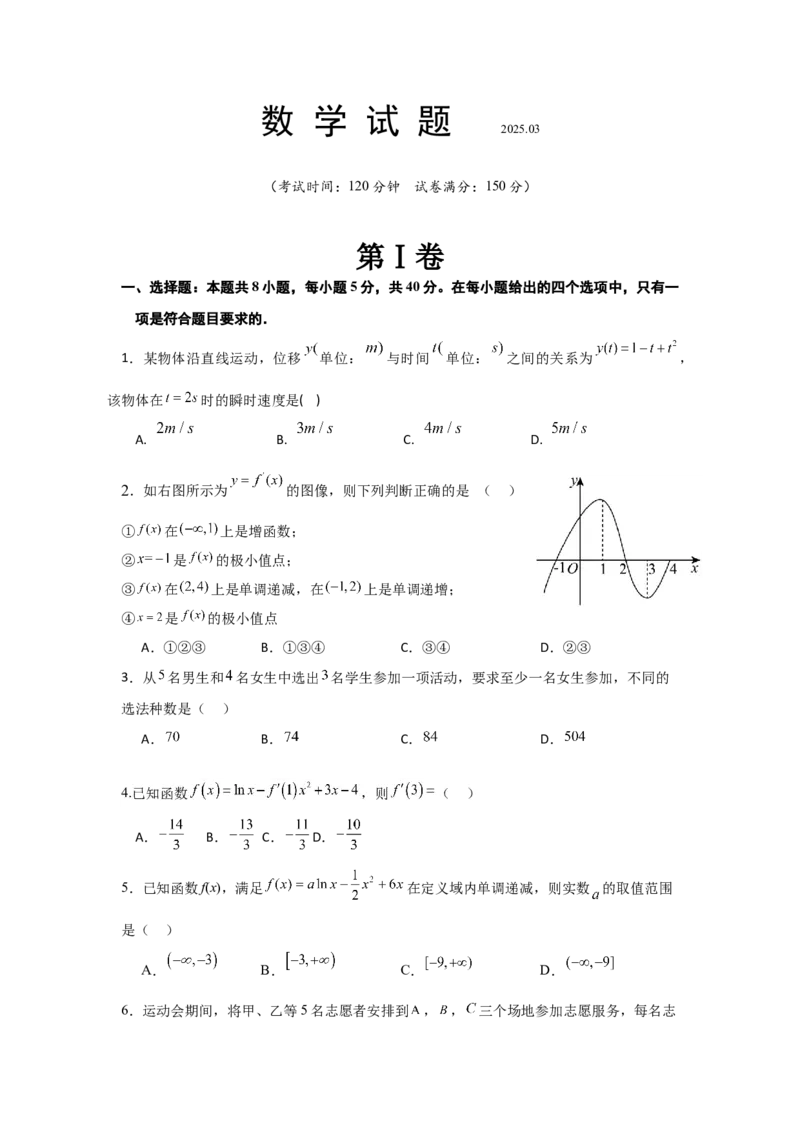
2.如右图所示为 的图像,则下列判断正确的是 ( )
① 在 上是增函数;
② 是 的极小值点;
③ 在 上是单调递减,在 上是单调递增;
④ 是 的极小值点
A.①②③ B.①③④ C.③④ D.②③
3.从 名男生和 名女生中选出 名学生参加一项活动,要求至少一名女生参加,不同的
选法种数是( )
A. B. C. D.
4.已知函数 ,则 ( )
A. B. C. D.
5.已知函数f(x),满足 在定义域内单调递减,则实数 的取值范围
是( )
A. B. C. D.
6.运动会期间,将甲、乙等5名志愿者安排到 , , 三个场地参加志愿服务,每名志愿者只能安排去一个场地,每个场地至少需要1名志愿者,且甲、乙两名志愿者不安排到
同一个场地,则不同的安排方法种数为( )
A.72 B.96 C.114 D.124
7.设函数 是定义在 上的奇函数, 为其导函数.当 时, ,
,则不等式 的解集为( )
A. B.
C. D.
8.若函数 恰有两个零点,则a的取值范围是( )
A. B. C. D.
二、多选题.本题共3小题,每题6分,共18分。在每小题给出的选项中,有多项符合题
目要求。
9.下列求导正确的是( )
A. B.
C. D.
10.为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”、
“乐”、“射”、“御”、“书”、“数”六门体验课程,每周一门,连续开设六周,则
下列说法正确的是( )
A.某学生从中选2门课程学习,共有15种选法
B.课程“乐”“射”排在相邻的两周,共有240种排法
C.课程“御”“书”“数”排在不相邻的三周,共有144种排法
D.课程“礼”不排在第一周,课程“数”不排在最后一周,共有480种排法11.已知函数 在 上可导且 ,其导函数 满足 ,对
于函数 ,下列结论正确的是( )
A.函数 在 上为增函数 B. 是函数 的极小值点
C.函数 必有 个零点 D.
第Ⅱ卷
三、填空题.本题共3小题,每小题5分,共15分。
12.函数 的图象在点 处的切线方程为 .
13.用数字0,1,2,3,5组成 个没有重复数字的五位偶数.
14.已知函数 , ,若关于 的不等式 有解,则
的最小值是 .
.四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤.
15.(13分)
(1)求值:
(2)求不等式: 的解集.
16.(15分)
已知函数 在点 处的切线 与直线 平行.
(1)求 的值及切线 的方程;
(2)求 的单调区间和极值.17.(15分)
从 , , ,D,E,F,G,H 8人中选出5人排成一排.
(1) 必须在内,有多少种排法?
(2) , 都在内,且 排在 前面,有多少种排法?
(3) , , 都在内,且 , 必须相邻, 与 , 都不相邻,都多少种排法?
(4) 不允许站排头和排尾, 不允许站在中间(第三位),有多少种排法?
18.(17分)
某商店销售一款酒精消毒液,每件的成本为4元,销售人员经调查发现,该款
消毒液的日销售量y(单位:件)与销售价格x(单位:元/件)满足关系式y=-x2+
14x-36(5≤x≤10,x∈N*).
(1)求该款消毒液的日利润w与销售价格x间的函数关系式;
(2)求当该款消毒液每件售价为多少元时,每日销售该款消毒液所获得的利润最
大,并求出日最大利润.
19.(17分)
已知函数 .
(1)讨论函数 的单调区间;
(2)当 时,证明: ;
(3)函数 有两个零点 、 ,求证: .