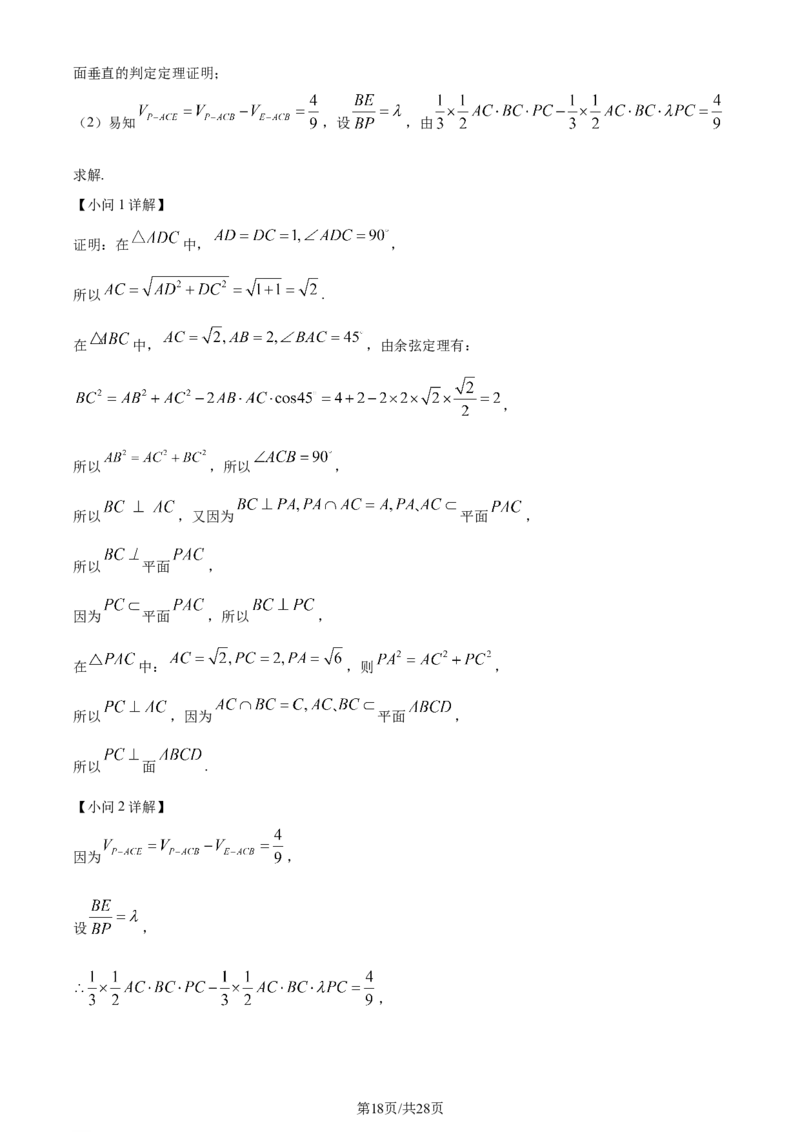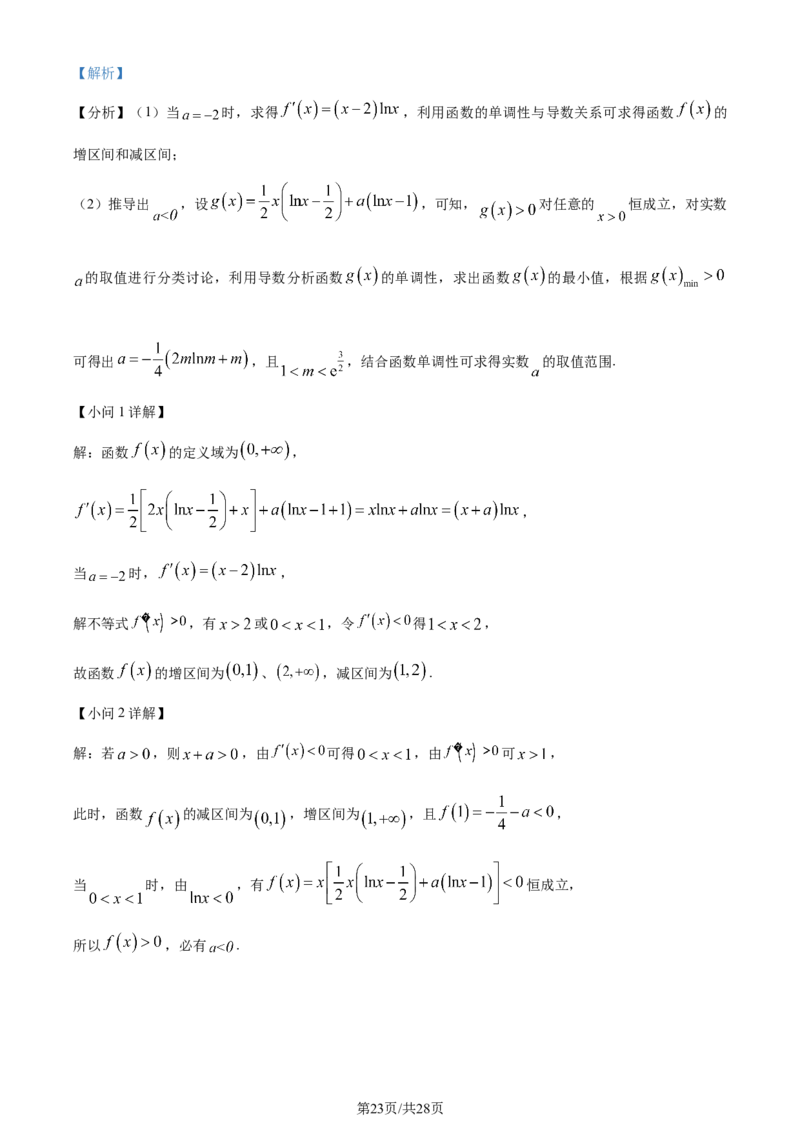文档内容
2023—2024 学年度下期高 2024 届二诊模拟考试
文科数学试卷
第I卷(选择题)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 ,则 ( )
A. B. C. D.
【答案】A
【解析】
【分析】根据根式与对数的定义域,结合交集的定义求解即可.
【详解】由 ,
所以 ,
故 ,
故选:A
2. 空间中有平面 和直线 , ,若 , ,则下列说法中一定错误的是( )
A. 直线 平行于平面 B. 直线 在平面 内
C. 直线 与平面 交于一点 D. 直线 和 共面
【答案】C
【解析】
【分析】根据线面平行及两直线平行得到 与平面 平行或直线 在平面 内,根据 ,可得直线
和 共面,从而判断出答案.
【详解】因为 ,所以 与平面 平行或直线 在平面 内,AB正确,C错误;
第1页/共28页
学科网(北京)股份有限公司因为 ,所以直线 和 共面,D正确.
故选:C
3. 已知 是虚数单位, ,则“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】由 结合复数相等求出 的值,再利用充分条件和必要条件的定义判断可得出结论.
【详解】若 ,且 ,则 ,解得 ,
所以,“ ”是“ ”的充分不必要条件.
故选:A.
4. 用反证法证明“平面四边形中至少有一个内角不超过 ”,下列假设中正确的是( )
A. 假设有两个内角超过 B. 假设四个内角均超过
C. 假设至多有两个内角超过 D. 假设有三个内角超过
【答案】B
【解析】
【分析】根据反证法的定义.
【详解】平面四边形中至少有一个内角不超过 的反面含义为
4个内角没有一个不超过 ,即四个内角均超过 ,
故选:B.
5. 年 月 日,第 届世界大学生夏季运动会(简称大运会)在四川成都开幕,这是继 北京
大运会, 深圳大运会之后,中国第三次举办夏季大运会;在成都大运会中,中国代表团取得了骄人
的成绩.为向大学生普及大运会的相关知识,某高校进行“大运会知识竞赛”,并随机从中抽取了 名
第2页/共28页
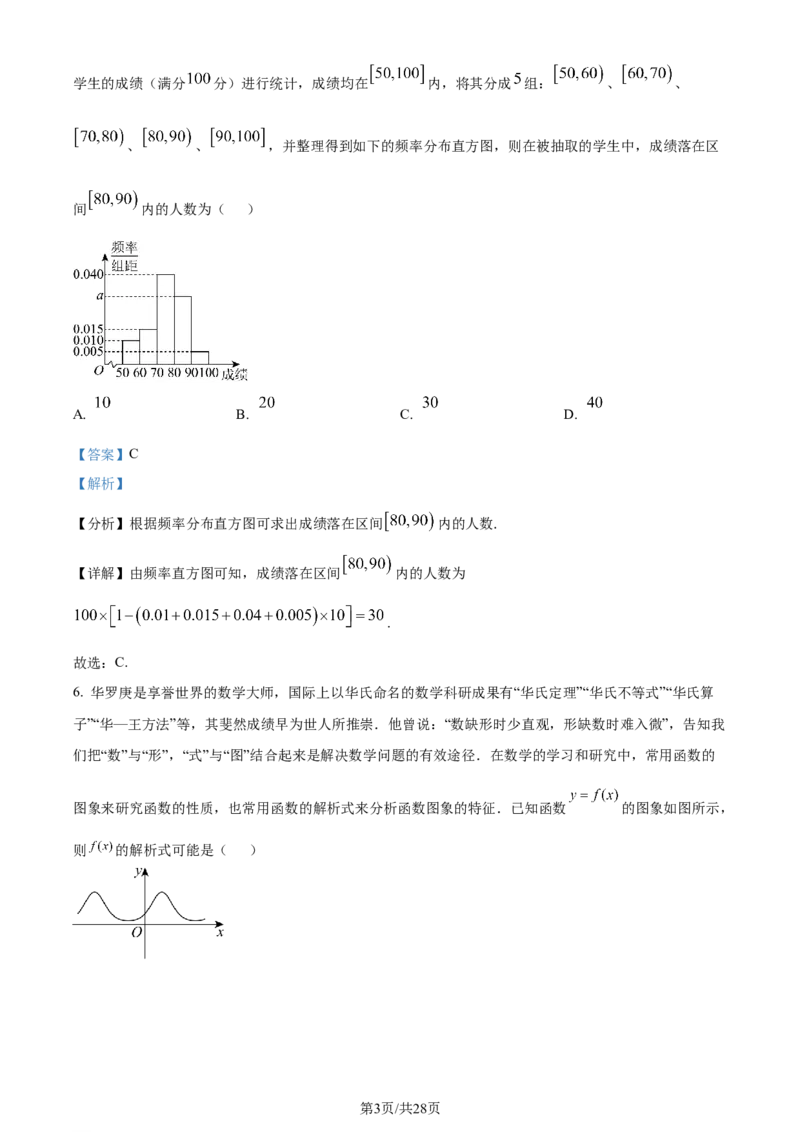
学科网(北京)股份有限公司学生的成绩(满分 分)进行统计,成绩均在 内,将其分成 组: 、 、
、 、 ,并整理得到如下的频率分布直方图,则在被抽取的学生中,成绩落在区
间 内的人数为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据频率分布直方图可求出成绩落在区间 内的人数.
【详解】由频率直方图可知,成绩落在区间 内的人数为
.
故选:C.
6. 华罗庚是享誉世界的数学大师,国际上以华氏命名的数学科研成果有“华氏定理”“华氏不等式”“华氏算
子”“华—王方法”等,其斐然成绩早为世人所推崇.他曾说:“数缺形时少直观,形缺数时难入微”,告知我
们把“数”与“形”,“式”与“图”结合起来是解决数学问题的有效途径.在数学的学习和研究中,常用函数的
图象来研究函数的性质,也常用函数的解析式来分析函数图象的特征.已知函数 的图象如图所示,
则 的解析式可能是( )
第3页/共28页
学科网(北京)股份有限公司A. B. C. D.
【答案】A
【解析】
【分析】利用指数函数、正弦函数的单调性、复合函数的单调性求解.
【详解】由函数图象可知, 的图象不关 轴对称,
而 , ,
即这两个函数均关于 轴对称,则排除选项 、 ;
由指数函数的性质可知 为单调递增函数, 为单调递减函数,
由 的图象可知存在一个极小的值 ,使得 在区间 上单调递增,
由复合函数的单调性可知, 在区间 上单调递增, 在区间 上单调
递减,
由图象可知 符合题意,
故选: .
7. 已知双曲线 的中心在原点,对称轴为坐标轴,且经过点 ,则下列结论中错误的是(
)
A. 的标准方程为 B. 的离心率等于
C. 与双曲线 的渐近线不相同 D. 直线 与 有且仅有一个公共点
【答案】C
【解析】
【分析】分别设出焦点在 轴上和在 轴上的双曲线方程求解即可求出双曲线 的标准方程,根据离心率
和渐近线方程的公式可求出离心率的值和渐近线方程,将直线方程和双曲线方程联立利用判别式即可判断
第4页/共28页
学科网(北京)股份有限公司双曲线和直线交点个数.
【详解】当双曲线的焦点在 轴上时,设双曲线的方程为 ,
则 ,解得 ,此时 的标准方程为 ,
当双曲线的焦点在 轴上时,设双曲线的方程为 ,
则 ,解得 (舍去),此种情况不成立,则 正确;
∵ ,∴ ,则 正确;
双曲线 的渐近线为 ,
双曲线 的渐近线为 ,即两者的渐近线相同,则 错误;
将直线 与双曲线 联立得 ,
,∴直线 与 有且仅有一个公共点,则 正确;
故选: .
8. 《周髀算经》中给出的弦图是由四个全等的直角三角形和中间一个小正方形拼成的一个大的正方形,若
下图中所示的角为 ( ),且小正方形与大正方形面积之比为 ,则 的值为(
)
第5页/共28页
学科网(北京)股份有限公司A. B. C. D.
【答案】D
【解析】
【分析】设大正方形 的边长为 ,求出小正方形 的边长,根据小正方形与大正方形面积之
比得 ,再利用弦化切求解可得答案.
【详解】如图,设大正方形 的边长为 ,
则小正方形 的边长为 ,
所以小正方形与大正方形面积之比为 ,
化简得 ,且 ,
由 ,
解得 .
故选:D.
第6页/共28页
学科网(北京)股份有限公司9. 已知 的内角A, , 所对的边分别为 , , ,面积为 ,若 ,
,则 的形状是( )
A. 等腰三角形 B. 直角三角形 C. 正三角形 D. 等腰直角三角形
【答案】B
【解析】
【分析】利用正弦定理的边角变换,结合诱导公式与倍角公式求得 B;利用面积公式与向量数量积的定义
求得A,从而得解
【详解】因为 ,所以 ,
因为 ,所以 ,所以 ,所以 ;
因为 ,所以 ,所以 ,所以 ,
所以 ,所以 ,
因为 ,所以 ,
所以 ,因为 ,所以 ,
所以 ,则 是直角三角形,
故选:B
10. 若函数 的最小值为 ,则函数 的最大值为( )
A. B. C. D.
【答案】A
【解析】
第7页/共28页
学科网(北京)股份有限公司【分析】分析函数解析式,发现函数 与函数 的变换关系,由此即可推断函数
的最大值.
【详解】 , ,
令 有: ,
则 ,即 ,
由此知 的函数图象为: 的图象通过横坐标变为原来的 ,纵坐标不变, 得到 ,
再关于 轴对称,得到 ,最后再向下平移一个单位,得到 ;
根据已知条件函数 的最小值为 ,
的
由此可知函数 最大值为 .
故选:A
11. 在四棱锥 中, 平面 ,且 .若点
均在球 的表面上,则球 的体积的最小值为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据题设易得 是四边形 外接圆的直径,利用线面垂直的性质、判定证
,进而得到 是以 为斜边的直角三角形,即 中
点 为外接球球心,令 且 ,求得外接球半径关于 的表达式,求其最小值,即可求
球体最小体积.
第8页/共28页
学科网(北京)股份有限公司【详解】
由题设, 在一个圆上,故 ,
又 ,所以 ,即 ,故 是四边形 外接圆的直径,
由 平面 , 平面 ,
则 ,
由 , 面 ,则 面 , 面 ,则 ,
由 , 面 ,则 面 , 面 ,则 ,则
,又 ,故 ,即 ,
令 且 ,则 , ,
且 都是以 为斜边的直角三角形,故 中点 为外接球球心,
所以外接球半径 ,
所以当 时, ,
此时球O的体积的最小值为 .
故选:C.
【点睛】关键点点睛:确定 是四边形 外接圆的直径, 中点 为外接球球心为本题的关键,
由此即可顺利得解.
第9页/共28页
学科网(北京)股份有限公司12. 已知函数 没有极值点,则 的最大值为( )
A. B. C. D.
【答案】B
【解析】
【分析】转化为 恒成立,构造函数,求导,得到其单调性和最值,从而得到
,故 ,换元后,构造函数,求导得到其单调性和最值,求出答
案.
详解】函数 没有极值点,
【
,或 恒成立,
由 指数爆炸的增长性, 不可能恒小于等于0,
恒成立.
令 ,则 ,
当 时, 恒成立, 为 上的增函数,
因为 是增函数, 也是增函数,
所以,此时 ,不合题意;
②当 时, 为增函数,由 得 ,
第10页/共28页
学科网(北京)股份有限公司令
在 上单调递减,在 上单调递增,
当 时,依题意有 ,
即 ,
, ,
令 , ,
则 ,
令 ,令 ,解得 ,
所以当 时, 取最大值
故当 , ,即 , 时, 取得最大值
综上,若函数 没有极值点,则 的最大值为
故选:B.
【点睛】关键点睛:将函数没有极值点的问题转化为导函数恒大于等于0,通过构造函数,借助导数研究
函数的最小值,从而得解.
第II卷(非选择题)
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知实数 ,若 ,则 的最小值为______.
第11页/共28页
学科网(北京)股份有限公司【答案】 ##
【解析】
【分析】由乘“1”的方法,利用基本不等式求最值.
【详解】由 ,
,
当且仅当 ,即 时,等号成立,
所以 的最小值为为 .
故答案为: .
14. 已知圆 的圆心与抛物线 的焦点关于直线 对称,直线 与圆 相交于
两点,且 ,则圆 的方程为______.
【答案】
【解析】
【分析】根据圆心与焦点关于直线 对称,求得圆心坐标,在此基础上由直线 与圆 相
交的弦长求得圆的半径.
【详解】由 的焦点坐标 关于直线 的对称点为 ,
所以圆 的圆心为 ,设半径为 ,
点C到直线 的距离为d,则 ,
第12页/共28页
学科网(北京)股份有限公司所以 ,
所以圆 的方程为: ,
故答案是: .
15. 已知直线 经过点 ,且被两条平行直线 和 截得的线段长为
,则直线 的方程为______.
【答案】 或
【解析】
【分析】直线 分斜率存在和不存在两种情况讨论;当斜率不存在时直线 是 轴,求交点坐标即可;当直
线 的斜率存在时,设定直线 的方程并与直线 的方程联立求交点,满足弦长即可.
【详解】若直线 的斜率不存在,则直线 的方程为: ,
此时与 的交点分别为 和 ,
截得的线段的长为: ,不符合题意.
若直线 的斜率存在,则设直线 的方程为: ,
解方程组 ,得点 ,
解方程组 ,得点 .
第13页/共28页
学科网(北京)股份有限公司由 ,得 ,
即 ,解得: ,
则直线 的方程为: 或 .
故答案是: 或 .
16. 已知椭圆 的左、右焦点分别为 ,离心率为 .若 和 为椭圆 上在
轴上方的两点,且 ,则直线 的斜率为______.
【答案】
【解析】
【分析】由离心率为 ,得到 间的关系,椭圆方程变为 ,借助椭圆的对称性,将关系式
转化直线 与椭圆的位置关系,设直线 的方程,联立椭圆方程,用韦达定理解决问题
即可.
【详解】已知椭圆 ,
由椭圆的离心率为 ,得 ,代入 ,得: ,
则椭圆 的方程为: ,
其左、右焦点分别为 ,
如图所示:若 和 为椭圆 上在 轴上方的两点,且 ,
第14页/共28页
学科网(北京)股份有限公司设直线 与椭圆 的另一个交点分别为 ,
由椭圆的对称性,可得: , , ,
即 ,
显然直线 的斜率定存在,否则直线 垂直 轴时 为线段 的中点,
因为点 在 轴上方,直线 的斜率不为零,
设直线 的方程为 , ,
联立方程组: ,
得: ,
(*),
由于 ,则 ,
(*)式即为: ,
消掉 后,可得: ,
化简可得: ,
第15页/共28页
学科网(北京)股份有限公司由于 , ,且 ,得 ,
所以 ,
故答案是: .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个
试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
17. 已知等差数列 的首项 ,公差为 为 的前 项和, 为等差数列.
(1)求 与 的关系;
(2)若 为数列 的前 项和,求使得 成立的 的最大值.
【答案】(1)
(2)7
【解析】
【分析】(1)由 为等差数列可得 ,即可得到 与 的关系;
(2)由裂项相消法得到 ,再解不等式即可求得n的最大值.
【小问1详解】
因为 为等差数列,所以 ,
第16页/共28页
学科网(北京)股份有限公司即 ,从而得到 ,
化简得 ,所以 .
【小问2详解】
当 时, ,
所以 ,
解得 ,又因为 ,所以 的最大值7.
18. 在四棱锥 中,已知 ,
是线段 上的点.
(1)求证: 底面 ;
(2)是否存在点 使得三棱锥 的体积为 ?若存在,求出 的值;若不存在,请说明理由.
【答案】(1)证明见解析
(2)存在点 使得三棱锥 的体积为 ,且
【解析】
【分析】(1)在 中,利用余弦定理求得BC,由 ,得到 ,再由
得到 平面 ,从而 ,然后由 得到 ,再利用线
第17页/共28页
学科网(北京)股份有限公司面垂直的判定定理证明;
(2)易知 ,设 ,由
求解.
【小问1详解】
证明:在 中, ,
所以 .
在 中, ,由余弦定理有:
,
所以 ,所以 ,
所以 ,又因为 平面 ,
所以 平面 ,
因为 平面 ,所以 ,
在 中: ,则 ,
所以 ,因为 平面 ,
所以 面 .
【小问2详解】
因为 ,
设 ,
,
第18页/共28页
学科网(北京)股份有限公司,
,
因此,存在点 使得三棱锥 的体积为 ,且 .
19. 2022年二十国集团领导人第十七次峰会11月16日在印度尼西亚巴厘岛闭幕,峰会通过《二十国集团
领导人巴厘岛峰会宣言》.宣言说,值此全球经济关键时刻,二十国集团采取切实、精准、迅速和必要的行动
至关重要,基于主席国印尼提出的“共同复苏、强劲复苏”主题,各国将采取协调行动,推进强劲、包容、韧性
的全球复苏以及创造就业和增长的可持续发展、中国采取负责任的态度,积极推动产业的可持续发展,并
对友好国家进行技术援助.非洲某芯片企业生产芯片I有四道工序,前三道工序的生产互不影响,第四道是
检测评估工序,包括智能自动检测与人工抽检.
(1)在中国企业援助前,该芯片企业生产芯片I的前三道工序的次品率分别为 .
求生产该芯片I的前三道工序的次品率 ;
(2)该芯片企业在中国企业援助下,改进生产工艺并生产了芯片II.某手机生产厂商获得芯片I与芯片II,
并在某款新型手机上使用.现对使用这款手机的用户回访,对开机速度进行满意度调查,据统计,回访的
100名用户中,安装芯片I的有40部,其中对开机速度满意的占 ;安装芯片II的有60部,其中对开
机速度满意的占 .现采用分层抽样的方法从开机速度满意的人群中抽取6人,再从这6人中选取2人进
行座谈,求抽到2人中对安装芯片II的手机开机速度满意的人数为1的概率.
【答案】(1)
(2)
【解析】
【分析】(1)由对立事件概率的关系即可求解;
第19页/共28页
学科网(北京)股份有限公司(2)先按分层抽样得出所抽取的6人中,手机安装芯片I的有2人,手机安装芯片II的有4人,结合超几
何分布的概率计算公式即可求解.
【小问1详解】
.
【小问2详解】
对安装芯片I的手机开机速度满意的人数为 ,对安装芯片II的手机开机速度满意的人数为
,
所以采用分层抽样的方法的抽样比为 ,
故所抽取的6人中,手机安装芯片I的有2人,手机安装芯片II的有4人,
所以抽到2人中对安装芯片II的手机开机速度满意的人数为1的概率为 .
20. 已知椭圆 的离心率为 ,短轴长为 ,过点 斜率存在且不为0的
直线 与椭圆有两个不同的交点 .
(1)求椭圆的标准方程;
(2)椭圆左右顶点为 ,设 中点为 ,直线 交直线 于点 是否为定
值?若是请求出定值,若不是请说明理由.
【答案】(1)
(2)是定值,为
【解析】
【分析】(1)根据条件列方程组,求出 的值,可得所求椭圆的标准方程;
第20页/共28页
学科网(北京)股份有限公司(2)由题设出直线 的方程 ,与椭圆方程联立可得根与系数关系,求得点 坐标,以及点
坐标,表示出 的斜率代入结合根与系数关系消元运算得解.
【小问1详解】
由题意: ,解得: ,
故所求椭圆的标准方程为: .
【小问2详解】
如图:因为直线 斜率不为0,设其方程为: ,
代入椭圆方程: ,得: ,整理得: .
设 ,则显然 ,则 ,
,则直线 方程为 ,
令 ,得 ,则 ,则 , , ,
第21页/共28页
学科网(北京)股份有限公司,
又 代入得
所以 为定值 .
【点睛】关键点点睛:本题第二问考查直线与椭圆的综合问题.求出 , ,
,代入化简,注意利用韦达定理,方程 将 代换成 ,再利用
,将 代换为 ,消元运算可得答案.
.
21 已知函数 ,其中 .
(1)当 时,求函数 的单调区间;
(2)若 ,求实数 的取值范围.
【答案】(1)函数 的增区间为 、 ,减区间为
(2)
第22页/共28页
学科网(北京)股份有限公司【解析】
【分析】(1)当 时,求得 ,利用函数的单调性与导数关系可求得函数 的
增区间和减区间;
(2)推导出 ,设 ,可知, 对任意的 恒成立,对实数
的取值进行分类讨论,利用导数分析函数 的单调性,求出函数 的最小值,根据
可得出 ,且 ,结合函数单调性可求得实数 的取值范围.
【小问1详解】
解:函数 的定义域为 ,
,
当 时, ,
解不等式 ,有 或 ,令 得 ,
故函数 的增区间为 、 ,减区间为 .
【小问2详解】
解:若 ,则 ,由 可得 ,由 可 ,
此时,函数 的减区间为 ,增区间为 ,且 ,
当 时,由 ,有 恒成立,
所以 ,必有 .
第23页/共28页
学科网(北京)股份有限公司又由 ,可得 .
又由 ,不等式 可化为 ,
设 ,
有 ,
当 且 时, , ,可得 ,
当 且 时, , ,可得 ,
当 时,函数 在 上单调递增,
故存在正数 使得 .
若 ,有 , ,有 ,
与 矛盾,可得 ,
当 时, ;当 时, ,
可得函数 的减区间为 ,增区间为 ,
若 ,必有 ,
有 ,
又由 ,有 ,
有 ,有 .
又由 ,有 ,可得 ,
有 ,可得 ,
第24页/共28页
学科网(北京)股份有限公司构造函数 ,其中 ,则 对任意的 恒成立,
所以,函数 在 上单调递增,
由 及 可得 ,可得 ,
若 ,则实数 的取值范围为 .
【点睛】关键点点睛:本题考查利用函数不等式恒成立求参数的取值范围,解本题的关键就是转化为
得出 ,再结合函数的单调性求出 的取值范围.
(二)选考题:共10分.请考生在第22、23题中选一题作答.如果多选,则按所做的第一题记
分.
【选修4-4:坐标系与参数方程】
22. 在直角坐标系 中,直线 的参数方程为 (t为参数, ),把 绕坐标原点
逆时针旋转 得到 ,以坐标原点O为极点,x轴正半轴为极轴,取相同的单位长度建立极坐标系.
(1)写出 , 的极坐标方程;
(2)若曲线 的极坐标方程为 ,且 与 交于点A, 与 交于点B(A,B与点O不重
合),求 面积的最大值.
【答案】22. ; .
23. 16
【解析】
第25页/共28页
学科网(北京)股份有限公司【分析】(1)通过消参得到直线 的直角坐标方程,再利用极坐标方程和直角坐标方程之间的互化公式
即可;
(2)利用极坐标的几何意义结合二倍角公式求解即可.
【小问1详解】
直线 的参数方程为 (t为参数, ),
故 ,则 ,即 ;
故 的极坐标方程为: .
把 绕坐标原点逆时针旋转 得到 ,故 的极坐标方程为: .
【小问2详解】
曲线 的极坐标方程为 ,
且 与 交于点A, 与 交于点B,
联立方程得, ,
故 .
故 面积的最大值为16.
【选修4-5:不等式选讲】
23. 已知函数 的最小值为 .
(1)求实数m的值;
(2)若实数a,b,c满足 ,证明: .
【答案】(1)
第26页/共28页
学科网(北京)股份有限公司(2)证明见解析
【解析】
【分析】(1)分类讨论x的取值,求出对应的函数解析式,结合图形即可求解;
(2)由(1)知 ,结合柯西不等式计算即可求解.
【小问1详解】
,
作出函数 的图形,如图,
由图可知 的最小值为 .
【小问2详解】
由(1)知, ,所以 ,
根据柯西不等式得 ,
当且仅当 时取等号,
又 ,所以当且仅当 时取等号,
第27页/共28页
学科网(北京)股份有限公司∴ .
第28页/共28页
学科网(北京)股份有限公司