文档内容
内江市高中 2025 届第一次模拟考试题
数学
本试卷共4页,19小题,满分150分,考试用时120分钟.
注意事项:
1.答题前,考生务必将自己的姓名、考号、班级用签字笔填写在答题卡相应位置.
2.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡
皮擦干净后,再选涂其它答案.不能答在试题卷上.
3.非选择题用签字笔将答案直接答在答题卡相应位置上.
4.考试结束后,监考人员将答题卡收回.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 在复平面内,复数 的对应点坐标为 ,则 的共轭复数为( )
A. B. C. D.
.
2 已知集合 , ,则 ( )
A. B. C. D.
3. 已知两个向量 , ,且 ,则 的值为( )
A. B. C. D.
4. “ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
.
C 充要条件 D. 既不充分也不必要条件
5. 已知一批产品中有 是合格品,检验产品质量时,一个合格品被误判为次品的概率为 ,一个次
品被误判为合格品的概率为 .任意抽查一个产品,检查后被判为合格品的概率为( )A. B. C. D.
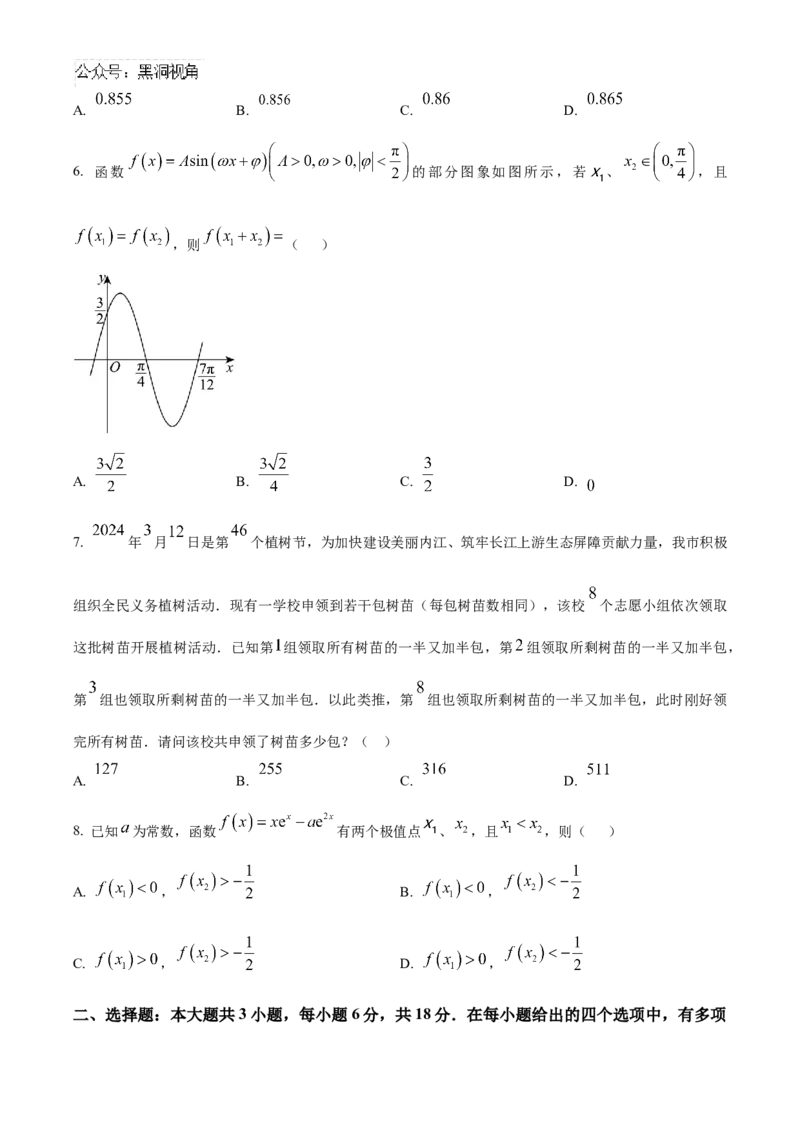
6. 函数 的部分图象如图所示,若 、 ,且
,则 ( )
A. B. C. D.
7. 年 月 日是第 个植树节,为加快建设美丽内江、筑牢长江上游生态屏障贡献力量,我市积极
组织全民义务植树活动.现有一学校申领到若干包树苗(每包树苗数相同),该校 个志愿小组依次领取
这批树苗开展植树活动.已知第 组领取所有树苗的一半又加半包,第 组领取所剩树苗的一半又加半包,
第 组也领取所剩树苗的一半又加半包.以此类推,第 组也领取所剩树苗的一半又加半包,此时刚好领
完所有树苗.请问该校共申领了树苗多少包?( )
A. B. C. D.
8. 已知 为常数,函数 有两个极值点 、 ,且 ,则( )
A. , B. ,
C. , D. ,
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 抛掷一枚质地均匀的骰子,观察骰子朝上面的点数,记随机事件 “点数为 ”,其中
,则下列论述正确的是( )
A.
B. 若 “点数大于 ”,则
C. 若连续抛掷骰子 次,记 “点数之和为 ”,则
D. 若重复抛掷骰子,则事件 发生的频率等于事件 发生的概率
10. 已知 ,则下列不等关系正确的有( )
.
A B.
C. D.
11. 给定函数 , .分别用 、 表示 、 中的最小者、最大
者,记为 , .下列说法正确的是( )
A.
B. 当直线 与曲线 有三个不同交点时,
C. 当 时,曲线 在点 处的切线与曲线 有且仅有一个交点
D. 函数 的值域为
三、填空题:本大题共3小题,每小题5分,共15分.12. 在 的展开式中,常数项为___________.
13. 在平行四边形 中,已知 , , ,点 在边 上, ,
的
与 相交于点 ,则 余弦值为______.
14. 已知函数 ( ,且 )的图象无限接近直线 但又不与该直线相
交,且 在 上单调递增,请写出一个满足条件的 的解析式______.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 在 中, , , 分别为内角 所对的边,且满足 .
(1)求 ;
(2)若 ,求 周长的最大值.
16. 已知数列 、 满足 , , , ,其中 、 、
.
(1)求数列 的通项公式;
(2)记 ,求数列 的前 项和 .
17. 已知函数 , .
(1)讨论函数 的单调性;
(2)若 恒成立,求实数 的取值范围.
18. 某市为全面提高青少年健康素养水平,举办了一次“健康素养知识竞赛”,分预赛和复赛两个环节,
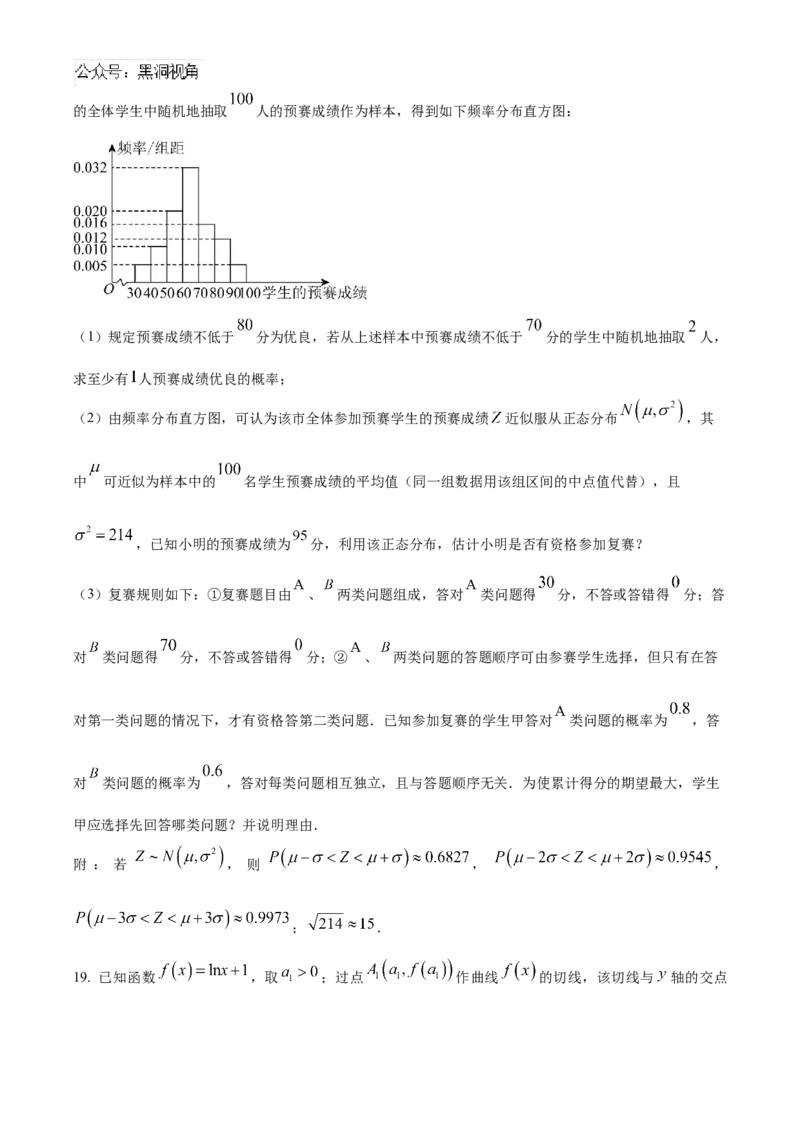
预赛成绩采用百分制,排名前三百名的学生参加复赛.已知共有 名学生参加了预赛,现从参加预赛的全体学生中随机地抽取 人的预赛成绩作为样本,得到如下频率分布直方图:
(1)规定预赛成绩不低于 分为优良,若从上述样本中预赛成绩不低于 分的学生中随机地抽取 人,
求至少有 人预赛成绩优良的概率;
(2)由频率分布直方图,可认为该市全体参加预赛学生的预赛成绩 近似服从正态分布 ,其
中 可近似为样本中的 名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且
,已知小明的预赛成绩为 分,利用该正态分布,估计小明是否有资格参加复赛?
(3)复赛规则如下:①复赛题目由 、 两类问题组成,答对 类问题得 分,不答或答错得 分;答
对 类问题得 分,不答或答错得 分;② 、 两类问题的答题顺序可由参赛学生选择,但只有在答
对第一类问题的情况下,才有资格答第二类问题.已知参加复赛的学生甲答对 类问题的概率为 ,答
对 类问题的概率为 ,答对每类问题相互独立,且与答题顺序无关.为使累计得分的期望最大,学生
甲应选择先回答哪类问题?并说明理由.
附 : 若 , 则 , ,
; .
19. 已知函数 ,取 ;过点 作曲线 的切线,该切线与 轴的交点记作 .若 ,则过点 作曲线 的切线,该切线与 轴的交点记作 .
以此类推得 ,直至 停止,由这些数构成数列 .
(1)若正整数 ,证明: ;
(2)若正整数 ,证明: ;
(3)若正整数 ,是否存在 使得 依次成等差数列?若存在,求出 的所有取值;若
不存在,请说明理由.