文档内容
河南省信阳高级中学 2023-2024 学年高三上期 11 月一模
数学试题
命题人:付其才 审题人:李艳
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中项是符合题目
要求的.
1.若集合 ,则 ( )
A. B. C. D.
2.已知 是单位向量,若 ,则 在 上的投影向量为( )
A. B. C. D.
3.设 ,则“ ”是“ ”的( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知 ,则 ( )
A. B. C. D.
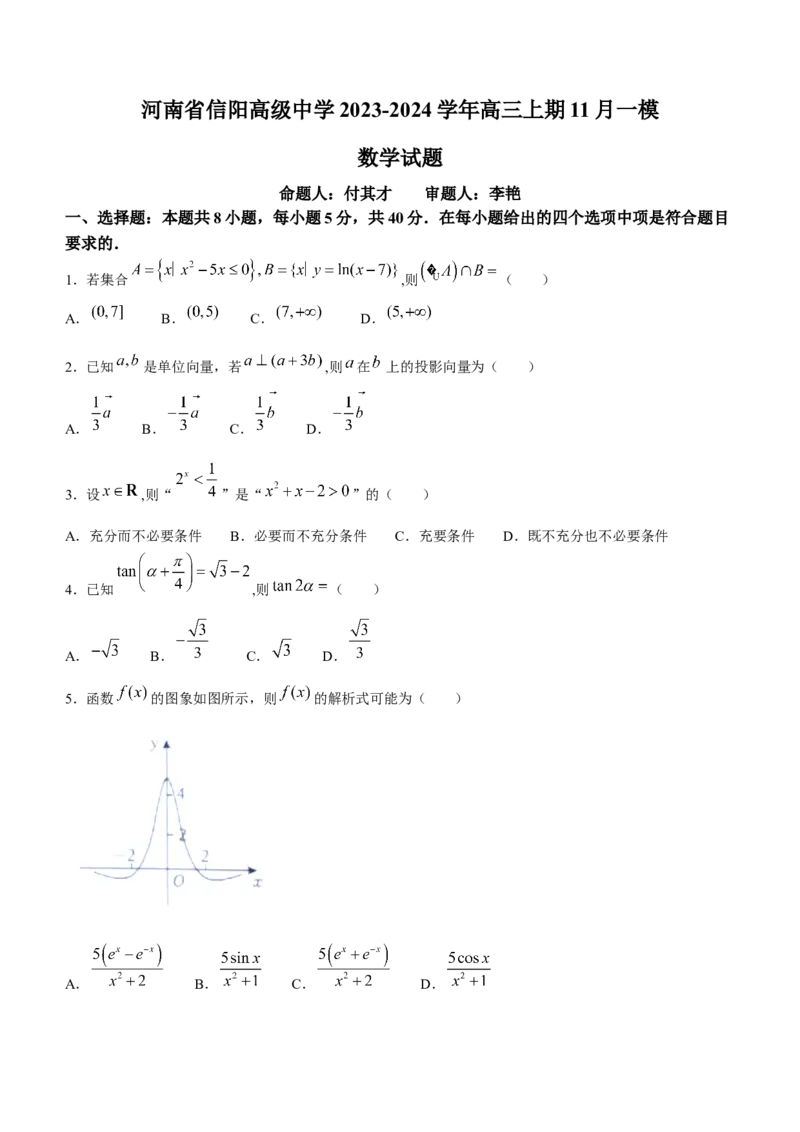
5.函数 的图象如图所示,则 的解析式可能为( )
A. B. C. D.6.尼知的数 ,若 在区间 内没有零点,则 的取
值范围是( )
A. B. C. D.
7.在四棱雉 中,底面 是直角梯形, .若
,且三棱雉 的外接球的表面积为 ,则当四棱雉 的体积最大值时,
长为( )
A. B.2 C. D.
8.已知 则( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.己知复数 ,下列命题正确的是( )
A. B.若 ,则 C. D.
10.己知等比数列 的公比为 ,前 项积为 ,若 ,则( )
A. B. C. D.
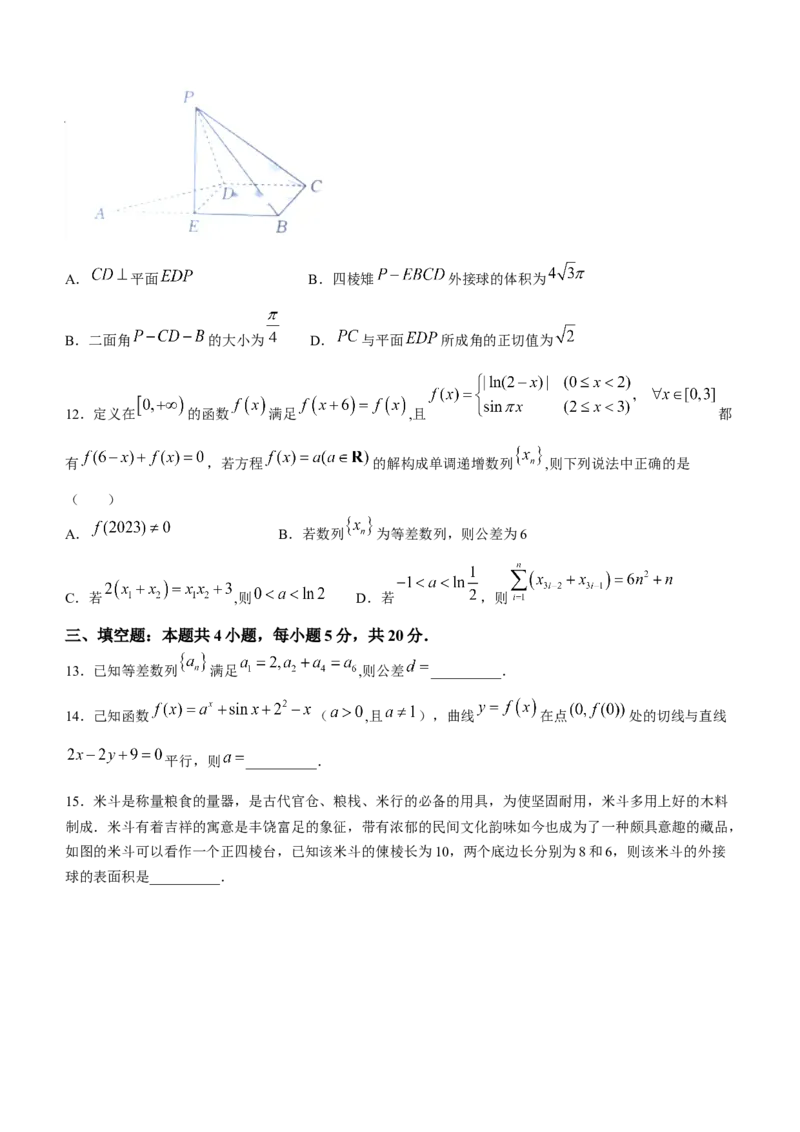
11.如图,直角梯形 中, 为 中点,以
为折痕把 折起,使点 到达点 的位置,且 .则下列说法正确的有( )A. 平面 B.四棱雉 外接球的体积为
B.二面角 的大小为 D. 与平面 所成角的正切值为
12.定义在 的函数 满足 ,且 都
有 ,若方程 的解构成单调递增数列 ,则下列说法中正确的是
( )
A. B.若数列 为等差数列,则公差为6
C.若 ,则 D.若 ,则
三、填空题:本题共4小题,每小题5分,共20分.
13.已知等差数列 满足 ,则公差 __________.
14.己知函数 ( ,且 ),曲线 在点 处的切线与直线
平行,则 __________.
15.米斗是称量粮食的量器,是古代官仓、粮栈、米行的必备的用具,为使坚固耐用,米斗多用上好的木料
制成.米斗有着吉祥的寓意是丰饶富足的象征,带有浓郁的民间文化韵味如今也成为了一种颇具意趣的藏品,
如图的米斗可以看作一个正四棱台,已知该米斗的倲棱长为10,两个底边长分别为8和6,则该米斗的外接
球的表面积是__________.16.己知函数 ,不等式 对任意的 恒成立,
则 的最大值为__________.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程及演算步骤.
17.(10分)己知函数 ,
(1)求关于 的不等式 的解集;
(2)若 在区间 上恒成立,求实数 的取值范围
18.(2分)已知函数 的图象相邻两条对称轴间的距离为 ,
函数 的最大值为2,且__________.
请从以下3个条件中任选一个,补充在上面横线上,① 为奇函数;②当 时 ;③
是函数 的一条对称轴并解答下列问题:
(1)求函数 的解析式;
(2)在 中, 分别是角 的对边,若 的面积 ,
求 的值.
19.(12分)己知数列 中,
(1)令 ,求证:数列 是等比数列;(2)令 ,当 取得最大值时,求 的值.
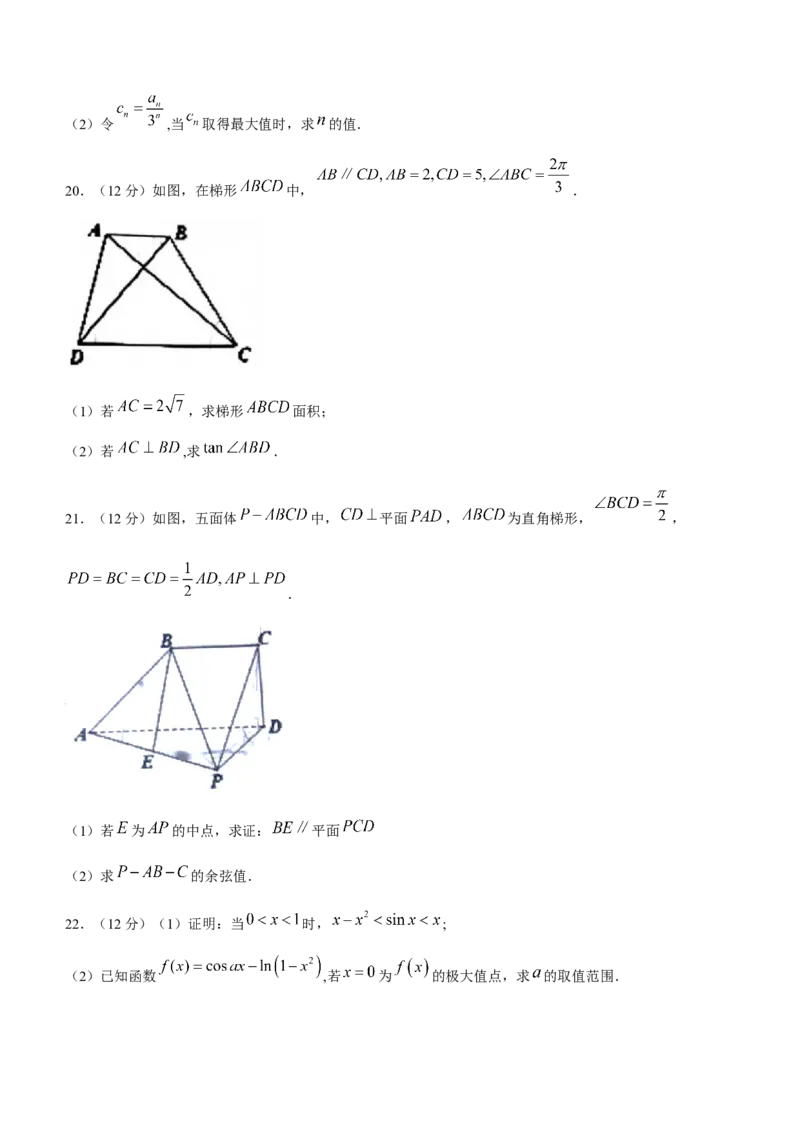
20.(12分)如图,在梯形 中, .
(1)若 ,求梯形 面积;
(2)若 ,求 .
21.(12分)如图,五面体 中, 平面 , 为直角梯形, ,
.
(1)若 为 的中点,求证: 平面
(2)求 的余弦值.
22.(12分)(1)证明:当 时, ;
(2)已知函数 ,若 为 的极大值点,求 的取值范围.