衡水名师卷·2023-2024高考模拟压轴卷（二）数学Word版含解析(1)_2024年5月_025月合集_2024届衡水名师卷·2023-2024高考模拟压轴卷（二）

2024 年普通高等学校招生全国统一考试模拟试题
数学（二）
本试卷共 4页，19小题，满分150分.考试用时 120分钟.
注意事项：
1.答题前，考生先将自己的姓名､准考证号码､考场号､座位号填写清楚，将条形码准确粘贴在
考生信息条形码粘贴区.
2.选择题必须使用 2B 铅笔填涂；非选择题必须使用 0.5毫米黑色字迹的签字笔书写，字体工
整､笔迹清楚.
3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿
纸､试卷上答题无效.
4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑.
5.保持卡面清洁，不要折叠，不要弄破､弄皱，不准使用涂改液､修正带､刮纸刀.
一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是
符合题目要求的.
15
1.已知点P  6,y  在焦点为F 的抛物线C:y2 2px(p0)上，若 PF  ，则 p（ ）
0
2
A.3 B.6 C.9 D.12
2.电影《孤注一郑》的上映引发了电信诈骗问题的热议，也加大了各个社区反电信诈骗的宣传力度.已知某
社区共有居民480人，其中老年人200人，中年人200人，青少年80人，若按年龄进行分层随机抽样，共
抽取36人作为代表，则中年人比青少年多（ ）
A.6人 B.9人 C.12人 D.18人
3.已知abc0，则下列说法一定正确的是（ ）
A.abc B.a2 bc
C.acb2 D.abbcb2 ac
4.已知向量a   2,3  ,b  1,2 ，则a  b  在a  b  方向上的投影向量为（ ）
 8 16  12 20 12 20  20 20
A. ,  B.  ,  C. ,  D.  , 
17 17  17 17 17 17  17 17
20 5π
5.已知某正六棱柱的体积为6 3，其外接球体积为 ，若该六棱柱的高为整数，则其表面积为（ ）
3
A.6 318 B.3 318 C.6 324 D.3 324
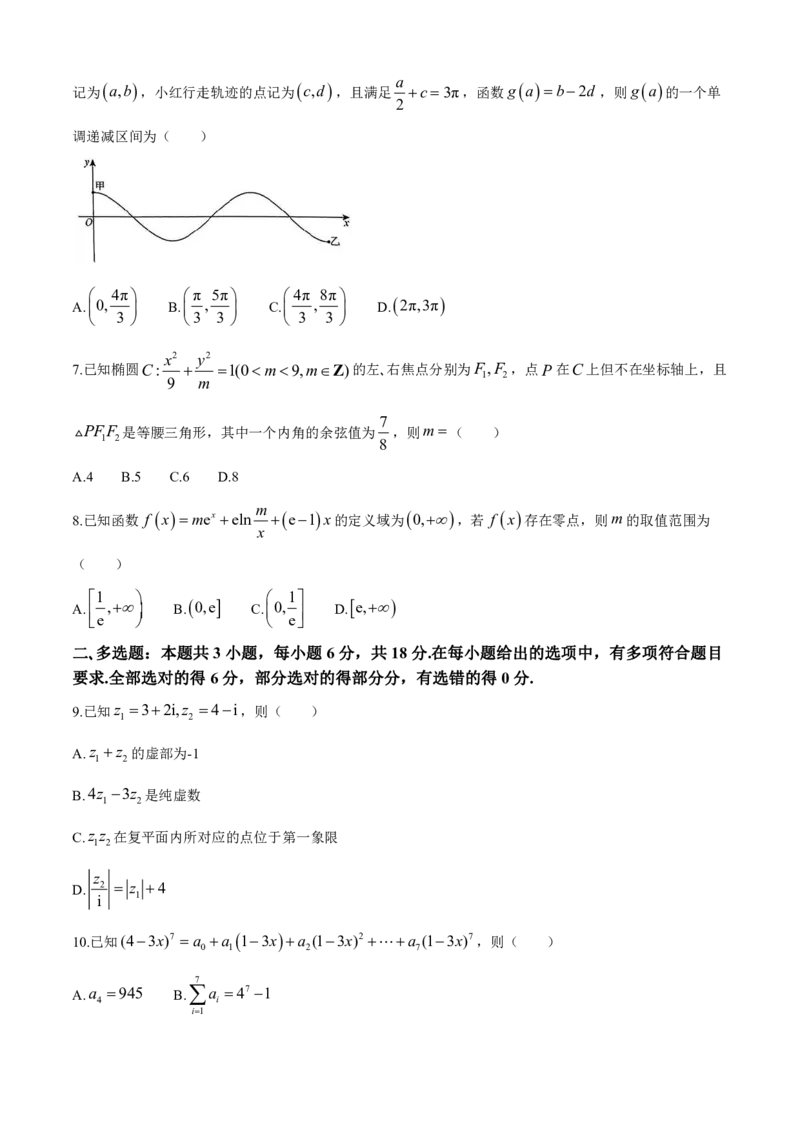
6.已知甲､乙两地之间的路线图如图所示，其可大致认为是 f

x
cosx 
0 x 3π

的图像.某日小明和小红
分别从甲､乙两地同时出发沿着路线相向而行，当小明到达乙地时，小红也停止前行.若将小明行走轨迹的点a
记为  a,b  ，小红行走轨迹的点记为  c,d  ，且满足 c3π，函数g  a b2d ，则g  a  的一个单
2
调递减区间为（ ）
 4π π 5π 4π 8π
 
A.0,  B. ,  C. ,  D. 2π,3π
 3  3 3   3 3 
x2 y2
7.已知椭圆C:  1(0m9,mZ)的左､右焦点分别为F,F ，点P在C上但不在坐标轴上，且
1 2
9 m
7
PFF 是等腰三角形，其中一个内角的余弦值为 ，则m（ ）
1 2
8
A.4 B.5 C.6 D.8
m
8.已知函数 f  x mex eln  e1  x的定义域为  0, ，若 f  x  存在零点，则m的取值范围为
x
（ ）
1   1
A. ,  B.  0,e  C.0,  D.  e,
e   e
二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目
要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分.
9.已知z 32i,z 4i，则（ ）
1 2
A.z z 的虚部为-1
1 2
B.4z 3z 是纯虚数
1 2
C.z z 在复平面内所对应的点位于第一象限
1 2
z
D. 2  z 4
i 1
10.已知(43x)7 a a  13x a (13x)2 a (13x)7，则（ ）
0 1 2 7
7
A.a 945 B. a 47 1
4 i
i1C.a a a a  21326 D.a a a a  26213
0 2 4 6 1 3 5 7
11.设M  x  是定义在N*上的奇因函数，是指x的最大奇因数，比如：M  3 3,M  6 3，M  8 1，
则（ ）
A.对kN*,M  2k1  M  2k 
B.M

2k

M

k

C.M

1
M 
2
M 
63
931
D.M  1263 63
三､填空题：本题共 3小题，每小题 5分，共 15分.
12.已知集合A  x∣4x2 x50  ,B {x∣xm}，若m0，则 ð A B __________；若AB R，
R
则m的取值范围为__________.
13.某校拟开设“生活中的数学”“音乐中的数学”“逻辑推理论”“彩票中的数学”和“数学建模”5门研究性学习课
程，要求每位同学选择其中2门进行研修，记事件A为甲､乙两人至多有1门相同，且甲必须选择“音乐中
的数学”，则P

A
__________.
14.定义：对于函数 f  x  和数列  x  ，若  x x  f x  f  x 0，则称数列  x  具有“ f  x  函数
n n1 n n n n
性质”.已知二次函数 f  x  图像的最低点为  0,4  ，且 f  x1  f  x 2x1，若数列  x  具有“ f  x 
n
函数性质”，且首项为1的数列  a  满足a ln  x 2 ln  x 2  ，记  a  的前n项和为S ，则数列
n n n n n n
 n 
S   5的最小值为__________.
 n 2 
四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤.
15.（13分）
b 2tanB
在ABC中，内角A,B,C所对的边分别为a,b,c，其中c 3 ，且 a  tanBtan  AB  .
（1）求C；
（2）求a2 b2的取值范围.
16.（15分）
 lnx
已知函数 f  x  xa .
 x 
 
（1）讨论 f x 的最值；kex x
（2）若a1，且 f  x  ，求k的取值范围.
x
17.（15分）
在如图①所示的平面图形中，四边形ACDE为菱形，现沿AC进行翻折，使得AB 平面ACDE，过点E
1
作EF ∥ AB，且EF  AB，连接FD,FB,BD，所得图形如图②所示，其中G为线段BD的中点，连
2
接FG.
（1）求证：FG 平面ABD；
7
（2）若AC  AD2，直线FG与平面BCD所成角的正弦值为 ，求AB的值.
7
18.（17分）
某汽车销售公司为了提升公司的业绩，现将最近300个工作日每日的汽车销售情况进行统计，如图所示.
（1）求a的值以及该公司这300个工作日每日汽车销售量的平均数（同一组中的数据用该组区间的中点值
作代表）；
 
（2）以频率估计概率，若在所有工作日中随机选择4天，记汽车销售量在区间 200,250 内的天数为X ，
求X 的分布列及数学期望；
（3）为增加销售量，公司规定顾客每购买一辆汽车可以进行一次抽奖活动，规则如下：抽奖区有A,B两个
盒子，其中A盒中放有9张金卡､1张银卡，B盒中放有2张金卡､8张银卡，顾客在不知情的情况下随机选
择其中一个盒子进行抽奖，直到抽到金卡则抽奖结束（每次抽出一张卡，然后放回原来的盒中，再进行下
次抽奖，中途可更换盒子），卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率
相同，求小明在首次抽奖抽出银卡的条件下，第二次从另外一个盒子中抽奖抽出金卡的概率.
19.（17分）
x2 y2
已知双曲线C:  1(a0,b0)的左顶点为A，直线l :y  x2与C的一条渐近线平行，且与C
a2 b2 11
交于点B，直线AB的斜率为 .
3
（1）求C的方程；
     
（2）已知直线l : y 2xm  m8  与C交于P,Q两点，问：是否存在满足EAEP  EPEQ  EAEQ
2
的点E  x ,y  ？若存在，求x2  y2的值；若不存在，请说明理由.
0 0 0 0数学（二）
一､选择题
p 15
1.A 【解析】由抛物线的定义可知 PF 6  ，解得 p3.故选A项.
2 2
200 x 80
2.B 【解析】设中年人抽取x人，青少年抽取y人，由分层随机抽样可知  , 
480 36 480
y
，解得x15,y 6，故中年人比青少年多9人.故选B项.
36
3.D
【解析】当a3,b2,c1时，abc，且acb2，故A，C项错误；因为ab0，ac0，
所以a2 bc，故B项错误；abbc  b2 ac   bc  ab 0，故D项正确.故选D项.
4.C 【解析】由题意得a  b   1,1  ,a  b   3,5 ，则a  b  在a  b  方向上的投影向量为
   
(ab)(ab)   12 20 
  (ab)  , ，故选C项.
|ab|2 17 17
4 20 5
5.D 【解析】设该正六棱柱的底面边长为a，高为h，其外接球的半径为R，易知 πR3  π，则
3 3
h2 3
R 5  a2  ①，且 a26h6 3②，联立①②，因为hZ，解得a1,h4，所以正六棱
4 4
3
柱的表面积S  a2126ah3 324.故选D项.
4
0 a 3π,
 a a 
6.A 【解析】依题意得bcosa,d cosccos3π  cos ，且 a 解得0 a 3π，
 2 2 0 3π 3π,
 2
a a a a
则g  a cosa2cos 2cos2 2cos 1，令t cos ，则t1,1  ，因为y2t2 2t1在区间
2 2 2 2
 1  1   4π  8π
 1, 内单调递减，在区间  ,1内单调递增，所以g  a  在区间0, ,2π, 内单调递减.故选
 2  2   3   3 
A项.
7.B 【解析】依题意得 PF  PF 6，设 FF n，不妨设点P在第一象限，则 PF  FF n，则
1 2 1 2 1 1 2
n2 n2 (6n)2 7 n2 (6n)2 n2 7
PF 6n(0n6)，故cosPFF   或cosPF F   ，
2 1 2 2n2 8 2 1 2n  6n  824 n 2
解得n4或n ，又mZ,m
 
9，所以n4,m5.故选B项.
11 2
8.C 【解析】由题意得m0，令 f  x 0，则exlnm e  xlnm elnx elnx.令g  x ex ex，易知
g  x  单调递增，所以g  xlnm  g  lnx  ，即xlnmlnx，即lnmlnxx.令h  x lnxx，则
1x
h x  ，当x 0,1  时，h x 0，h  x  单调递增，当x 1, 时，h x 0,h  x  单调递减，
x
1
又h  1 1，当x0时，h  x ，所以lnm 1，解得0m .故选C项.
e
二､多选题
9.BC 【解析】z z 7i的虚部为1，故A项错误；4z 3z 11i为纯虚数，故B项正确；
1 2 1 2
z z  32i  4i 145i，其在复平面内所对应的点  14,5  位于第一象限，故C项正确；
1 2
z 4i
2   14i  17 ， z 4 134，故D项错误.故选BC项.
i i 1
1
10.AC 【解析】依题意得(43x)7 [3 13x  ]7，所以a C433 3527945，故A项正确；令x  ，
4 7 3
7 7 2
得a 3，令x0，得 a 47，所以 a 47 37，故B项错误；令x ，得
0 i i
3
i0 i1
27 a a a a a a a a ①，又47 a a a a a a a a ②，由①+②可得
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7
47 27
a a a a  21325，故C项
0 2 4 6 2
正确；同理，由②-①得a a a a  21326，故D项错误.故选AC项.
1 3 5 7
11.ABD 【解析】由题意得M  2k  M  k  ，故B项正确；M  2k  M  k  k,M  2k1 2k1 k，
故A项正确；
163
12363 632563，所以M  12363  M  63 63，故D项正确；
2
M

1
M 
2
M 
63
[M 
1

M

3
M 
63

M

2
M 
4

M

62
1363
M

1
M  2 M  31 

210 

M  1 
M

3
M 
31

M

2
M 
4

M  30  ]210 28 26 24 22 20 
146
1365，故C项错误.故选ABD项.
14
三､填空题
 5 5
12.x 0 x  ,1  【解析】集合A x∣x1或x  ，所以ð A
 4 4 R
 5
Bx 0 x .若AB R，结合数轴可知m1，故m的取值范围为(,1).
 4
9
13. 【解析】若甲､乙两人的选课都不相同则共有C1C2 4312种；若甲､乙两人的选课有1门相同，
25 4 3
1224 9
则共有2C2 C1C1 24种.故P  A   .
4 4 3 C2C2 25
5 5
511
14.- 【解析】由题意知 f  x ax2 4(a 0)，又 f  x1  f  x a  2x1 2x1，所以a1，
2
x 2
则 f  x  x2 4.由题意得a ln  x 2 ln  x 2 ln n ，
n n n x 2
n
f  x  x2 4 x2 4
由  x x  f x  f  x 0，得x  x  n ，即x  x  n  n ，又
n1 n n n n1 n f x  n1 n 2x 2x
n n n
 x 2 2  x 2 2 x 2  x 2 2 x 2 x 2
x 2 n ,x 2 n ，所以 n1  n ，则ln n1 2ln n ，即
n1 2x n1 2x x 2  x 2 2 x 2 x 2
n n n1 n n1 n
a 2a ，故  a  是以1为首项，2为公比的等比数列，所以a 2n1,S 2n 1.令c  S .
n1 n n n n n n
  n 5      n 5     2n1  ，则c c  n8 2n1 1 ，故当n 8时，
2  2  n1 n 2
511
c c ，当n 9时，c c ，故 c  c  .
n1 n n1 n n min 9 2
四､解答题
15.解：（1）因为tan  AB  tan  πC tanC ，b 2tanB
所以  ，
a tanBtanC
sinB 2tanB
由正弦定理得  
sinA tanBtanC
2sinBcosC 2sinBcosC
 
sinBcosCcosBsinC sin  BC 
2sinBcosC
sinA
因为sinA0,sinB0，所以2cosC 1，
1
则cosC  ，
2
π
又C 0,π  ，所以C  .
3
（2）由余弦定理得3a2 b2 ab，
a2 b2
因为 ab，
2
a2 b2 a2 b2
所以a2 b2 ab a2 b2   ,
2 2
即a2 b2 6.当且仅当ab 3时等号成立.
又a2 b2 3ab，且ab0，
所以a2 b2 3.
 
综上，a2 b2的取值范围为 3,6 .
16.解：（1）由题意得 f

x

的定义域为
 0,
，
1 ax1
f x a  ,
x x
当a
0,x 0,
时，
f
x
0，
所以 f

x

在区间
 0,
内单调递减，无最值；1
当a0时，令 f x 0，得x ，
a
 1
当x 0, 时， f x 0, f  x  单调递减，
 a
1 
当x  , 时， f x 0, f  x  单调递增.
a 
1 1
故当x 时， f  x  取得最小值，且最小值为 f   1lna ，无最大值.
a a
综上，当a 0时， f  x  无最值；当a0时， f  x  的最小值为1lna，无最大值.
kex x
（2）当a1时，由 f  x  ，
x
kex x
得xlnx ，
x
整理得kex x2 xxlnx，
x2 xxlnx
即k .
ex
x2 xxlnx
令h  x  ，
ex
 2x1lnx1  ex  x2xxlnx  ex
则h x  
 ex2
 xlnx  1x 
 ，
ex
由（1）知，当a1时， f  x  xlnx的最
小值为 f

1
10，
即xlnx0恒成立，
所以当x
0,1
 时，h
x
0,h 
x

单调递增；
当x 1, 时，h
x
0,h 
x

单调递减.
2 2
故当x1时，h  x  取得最大值h  1  ，即k ，
e e2 
故k的取值范围为  , .
e 
17.（1）证明：连接CE交AD于点O，连接GO.在菱形ACDE中，CE  AD，
因为AB 平面ACDE,CE平面ACDE，所以CE  AB，
又ABAD A,AB,AD平面ABD，
所以CE 平面ABD.
因为G,O分别为BD,AD的中点，
1
所以GO  AB,GO ∥ AB，
2
1
又EF  AB,EF ∥ AB，
2
所以GO∥EF ，
所以四边形GOEF 为平行四边形，
所以FG∥ EO，所以FG 平面ABD.
（2）解：在菱形ACDE中，因为AC  AD，
所以ACD和ADE都是正三角形，
取ED的中点H ，连接AH ，则AH  AC，
又AB 平面ACDE，所以AB AC,AB AH ，即AB,AC,AH 两两垂直.
以A为坐标原点，AB,AC,AH 所在直线分别为x,y,z轴，建立如图所示的空间直角坐标系，
设AB2a(a0)，
 1 3
则C(0,2,0),B(2a,0,0),D(0,1, 3),F(a, 1, 3),G a, , 
 
 2 2 
 
则BC 2a,2,0  ,CD (0,1，  3 3
3),FG 0, ,  .
 
2 2
 

设平面BCD的法向量为m
x,y,z

，


 mBC 2ax2y  0,
则 

mCD y 3z  0,
  3 
取z 1，则m , 3,1.
 
a
 
记直线FG与平面BCD所成角为，
  3 7
  |FGm|  ,
则sin|cosFG,m|   . 3 7
|FG||m| 4 3
a2
解得a1，即AB的值为2.
18.解：（1）依题意得(0.0010.0020.0032a0.006)501.
解得a0.004.
所求平均数为250.1750.15125
0.21750.32250.22750.05150.
 1
（2）依题意得X B4, ，
 5
4
4 256
则P  X 0     ，
5 625
3
1 4 256
P  X 1 C1     
4 5 5 625
2 2
1 4 96
P  X 2 C2       ,
4 5 5 625
3
1 4 16
P  X 3 C3    
4 5 5 625
4
1 1
P  X 4    
5 625
X 0 1 2 3 4256 256 96 16 1
P
625 625 625 625 625
1 4
故E  X 4  .
5 5
（3）设“选到A盒”为事件A，“选到B盒”为事件A ，，摸到金卡”为事件B ，，摸到银卡”为事件B ，
1 2 1 2
因为B,B 是对立事件，
1 2
1 9 1 2 11
所以P  B      .
1 2 10 2 10 20
9
P

B
1P 
B

.
2 1 20
1
由题意得P  A  P  A  ，
1 2 2
 
P AB
所以P  A∣B  1 2 
1 2 P  B 
2
1 1
P  B∣ 2 A 1  P  A 1   10  2  1 ,
P  B  9 9
2
20
8
则P  A∣B 1P  A∣B  .
2 2 1 2 9
8 9 1 2 37
故所求的概率P      .
9 10 9 10 45
19.解：（1）易知C的一条渐近线方程为y  x，
则ab.
设B  t,t2  ，
1
又A a,0  ,a 0，直线AB的斜率为 ，
3
t2 1
所以  ，
ta 3
6a 6a 2a
解得t  ，则B , ，
2  2 2 代入x2 y2 a2中，解得a4.
x2 y2
故C的方程为  1.
16 16
   
（2）因为EAEP  EPEQ，
  
 
所以EP EAEQ 0，
 
即EPQA0，所以PE  AQ，
同理可得AE PQ,EQ AP.
   
设P x ,y ,Q x ,y ，
1 1 2 2
x2 y2
  1,
联立16 16 整理得3x2 4mxm2 160，

y 2xm.
 
由题意知Δ 16m2 12 m2 16 0，且m8，
解得m4 3或m4 3，且m8，
4m m2 16
所以x x  ,x x  .
1 2 3 1 2 3
1
过点A与l 垂直的直线的方程为 y  x2，设该直线与C的右支交于另一点H ，
2
2
x2 y2

 1,
16 16 20
联立 整理得3x2 8x800，解得x 或x4（舍去）.
 1 3
y x2,

2
20 16
所以H , .
 3 3 
  20 16  20 80 16
因为PH AQ   x ,  y   x  4y  x  x x 4x  y 
 3 1 3 1  2 2 3 2 3 1 2 1 3 2
20 80 16
y y  x  x x 4x   2x  m) 2x m  2x m 5x x (1
1 2 3 2 3 1 2 1 3 2 1 2 1 2
80 16 m2 16  4  80
2m)  x x   mm2 5   42m    m  
1 2 3 3 3  3  316 5 80 16 8 80 16
mm2  m2   m m2   mm2 0
3 3 3 3 3 3 3
所以PH  AQ，同理可证QH  AP.
又AH  PQ，所以H 与E重合.
因为H 在C上，所以x2  y2 16.
0 0
     
故存在点E满足EAEP  EPEQ  EAEQ ，且x2  y2的值为16.
0 ij