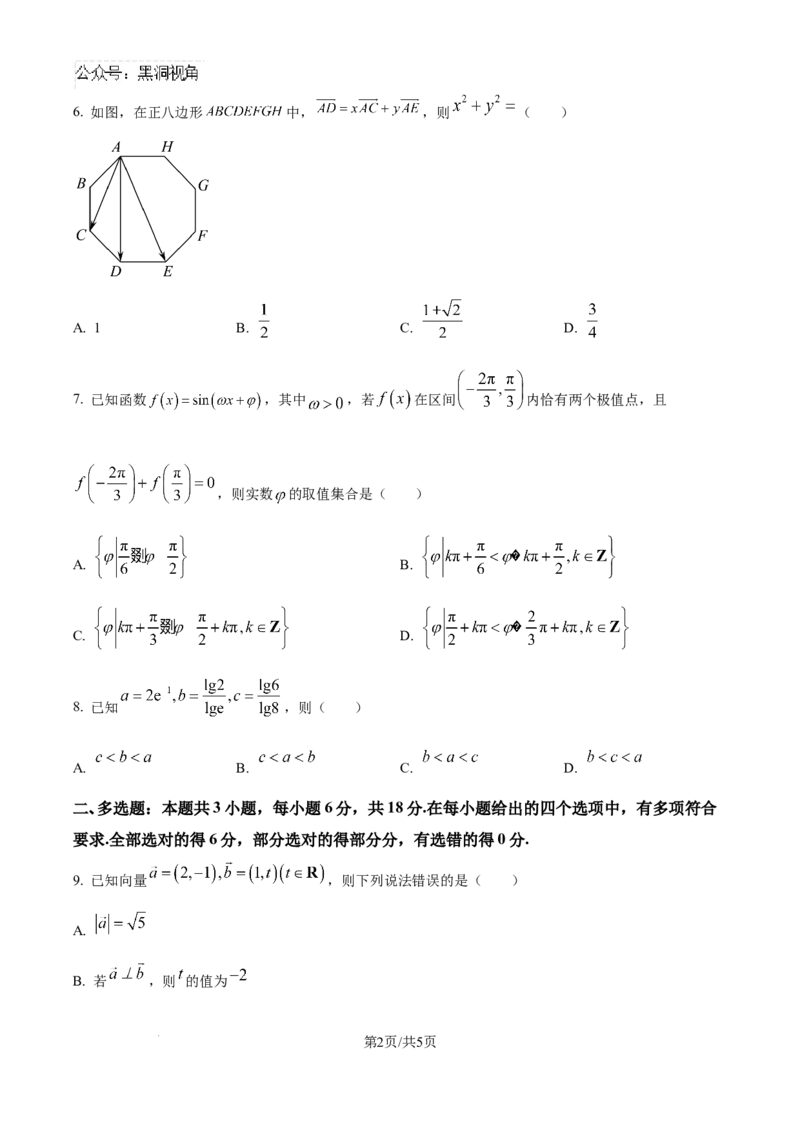文档内容
固镇县毛钽厂实验中学 2024~2025 学年高三 11 月月考
数学
考生注意:
1.满分150分,考试时间120分钟.
2.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B铅笔把答题卡上对应
题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区
域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
3本卷命题范围:集合与常用逻辑用语、不等式、函数、一元函数的导数及其应用、三角函数、平
面向量、数列(数列的概念、等差数列).
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 已知集合 ,则 中元素的个数为( )
A. 9 B. 8 C. 5 D. 4
2. 等差数列 满足 , ,则 ( )
A. B. C. D.
3. 函数 在区间 上的最小值为( )
.
A 2 B. 3 C. 4 D. 5
4. 已知 ,则 ( )
.
A B. C. D. 1
5. 在 中,若 ,则 的形状是( )
A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰或直角三角形
第1页/共5页
学科网(北京)股份有限公司6. 如图,在正八边形 中, ,则 ( )
A. 1 B. C. D.
7. 已知函数 ,其中 ,若 在区间 内恰有两个极值点,且
,则实数 的取值集合是( )
A. B.
C. D.
8. 已知 ,则( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知向量 ,则下列说法错误的是( )
A.
B. 若 ,则 的值为
第2页/共5页
学科网(北京)股份有限公司C. 若 ,则 的值为
D. 若 ,则 与 的夹角为锐角
10. 朱世杰(1249年—1314年),字汉卿,号松庭,元代数学家、教育家,毕生从事数学教育,有“中世纪
世界最伟大的数学家”之誉.他的一部名著《算学启蒙》是中国最早的科普著作,该书中有名的是“堆垛问
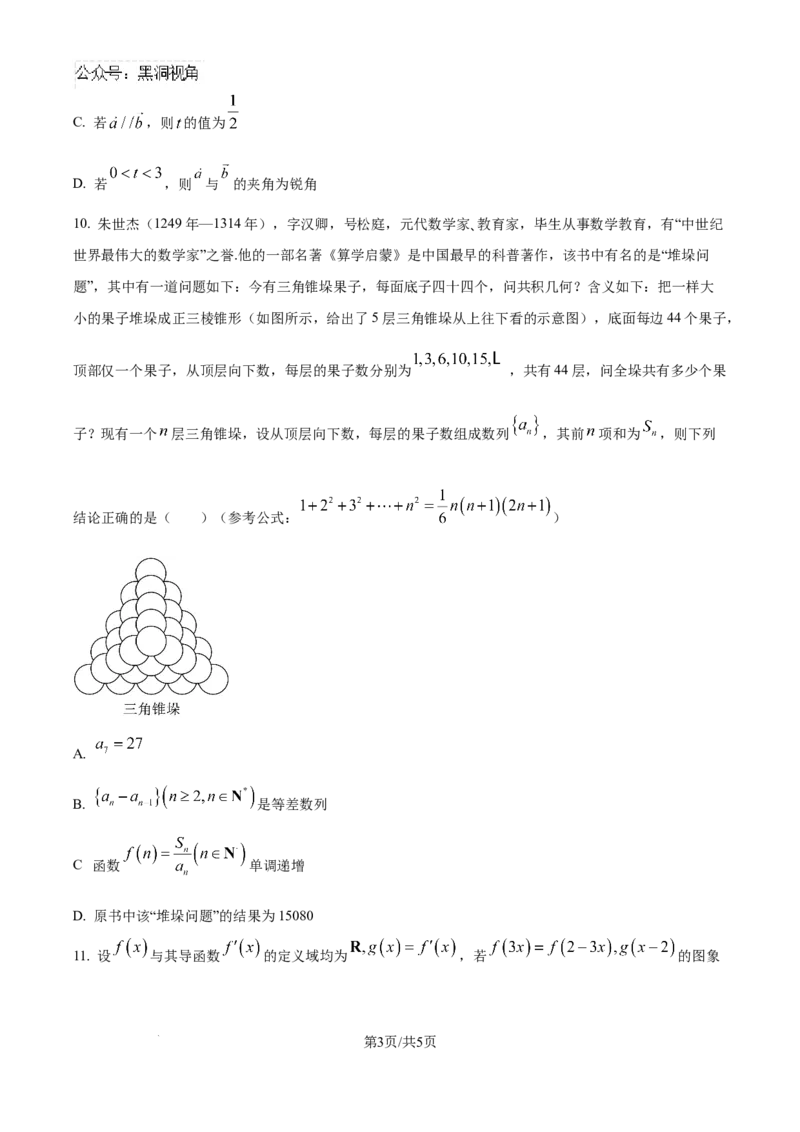
题”,其中有一道问题如下:今有三角锥垛果子,每面底子四十四个,问共积几何?含义如下:把一样大
小的果子堆垛成正三棱锥形(如图所示,给出了5层三角锥垛从上往下看的示意图),底面每边44个果子,
顶部仅一个果子,从顶层向下数,每层的果子数分别为 ,共有44层,问全垛共有多少个果
子?现有一个 层三角锥垛,设从顶层向下数,每层的果子数组成数列 ,其前 项和为 ,则下列
结论正确的是( )(参考公式: )
A.
B. 是等差数列
.
C 函数 单调递增
D. 原书中该“堆垛问题”的结果为15080
11. 设 与其导函数 的定义域均为 ,若 的图象
第3页/共5页
学科网(北京)股份有限公司关于 对称, 在 上单调递减,且 ,则( )
A. 为偶函数 B. 的图象关于原点对称
C. D. 的极小值为3
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知扇形的半径为 ,圆心角为 ,若 ,则该扇形的面积为__________.
13. 已知等差数列 的首项为 ,前 项和为 ,若 ,且 ,则 的取值范
围为__________.
14. 若对任意 ,不等式 恒成立,则实数 值的是__________.
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.
15. 已知 、 、 为 的三个内角,向量 与
共线,且 .
(1)求角 的大小;
(2)求函数 的值域.
16. 已知数列 的前 项和为 且 .
(1)求证:数列 是等差数列;
(2)设 ,求数列 的前90项的和.
17. 如图,在四边形 中. , , , 平分 且 与 相交
于点 .
第4页/共5页
学科网(北京)股份有限公司(1)若 的面积为 ,求 ;
(2)若 ,求 与 的面积之比.
.
18 已知函数 .
(1)讨论函数 的单调性;
(2)当 时,求证: .
19. 对于函数 ,若存在正常数 ,使得对任意的 ,都有 成立,我们
称函数 为“ 同比不减函数”.
(1)求证:对任意正常数 , 都不是“ 同比不减函数”;
(2)若函数 是“ 同比不减函数”,求 的取值范围;
(3)是否存在正常数 ,使得函数 为“ 同比不减函数”,若存在,求 的取值
范围;若不存在,请说明理由.
第5页/共5页
学科网(北京)股份有限公司