2002年江苏高考数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_江苏

2002 年江苏高考数学真题及答案 一、选择题（共12小题，每小题5分，满分60分） sin2x 1．（5分）函数 f(x) 的最小正周期是( ) cos2x  A． B． C．2 D．4 2 3 2．（5分）圆(x1)2  y2 1的圆心到直线y x的距离是( ) 3 1 3 A． B． C．1 D． 3 2 2 3．（5分）不等式(1x)(1|x|)0的解集是( ) A．{x|0„ x1} B．{x|x0且x1} C．{x|1x1} D．{x|x1且 x1} 4．（5分）在(0,2)内，使sinxcosx成立的x的取值范围是( )    5  A．( ， ) (， ) B．( ，) 4 2 4 4  5   5 3 C．( ， ) D．( ，) ( ， ) 4 4 4 4 2 k  k  5．（5分）已知集合M {x|x  ，kZ}，N {x|x  ，kZ}，则( ) 2 4 4 2 A．M N B．M  N C．M  N D．M N   6．（5分）一个圆锥和一个半球有公共底面，如果圆锥的体积与半球的体积恰好相等，则圆 锥轴截面顶角的余弦值是( ) 3 4 3 3 A． B． C． D． 4 3 5 5 7．（5分）函数 f(x)x|xa|b是奇函数的充要条件是( ) A．ab0 B．ab0 C．ab D．a2 b2 0 8．（5分）已知0x ya1，则有( ) A．log (xy)0 B．0log (xy)1 C．1log (xy)2 D．log (xy)2 a a a a 1 9．（5分）函数y1 ( ) x1 A．在(1,)内单调递增 B．在(1,)内单调递减 第1页 | 共14页C．在(1,)内单调递增 D．在(1,)内单调递减 1 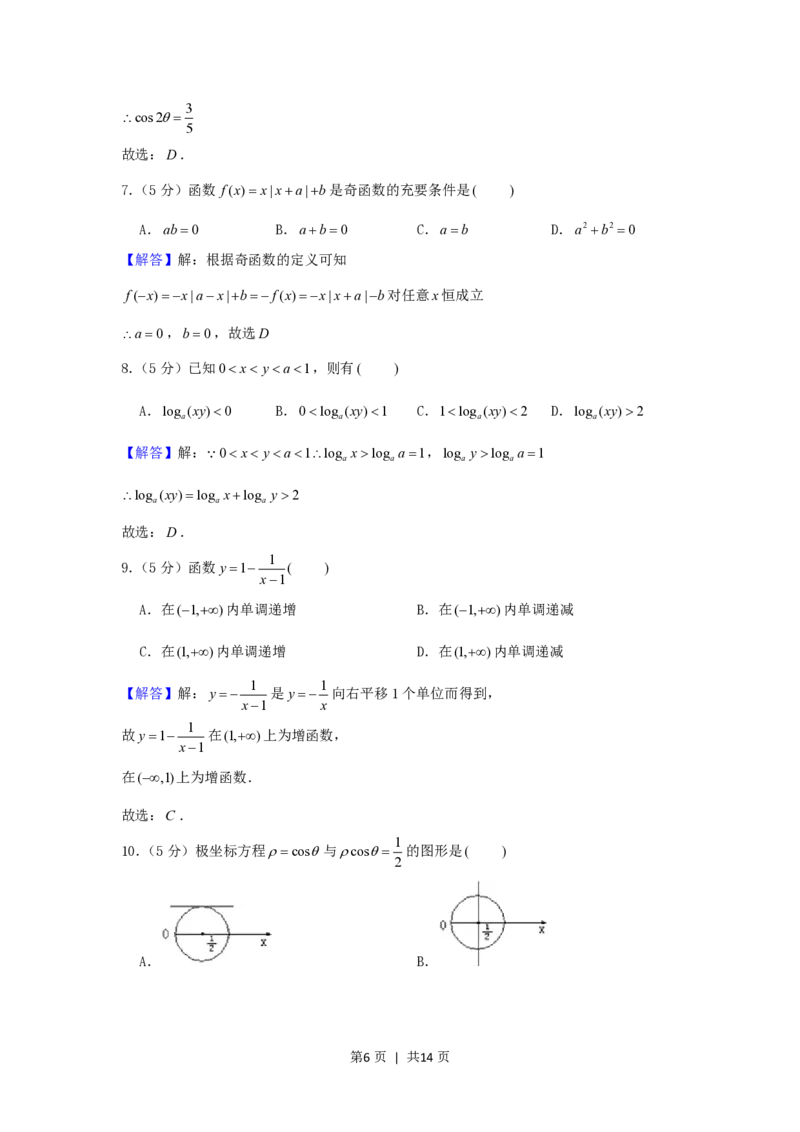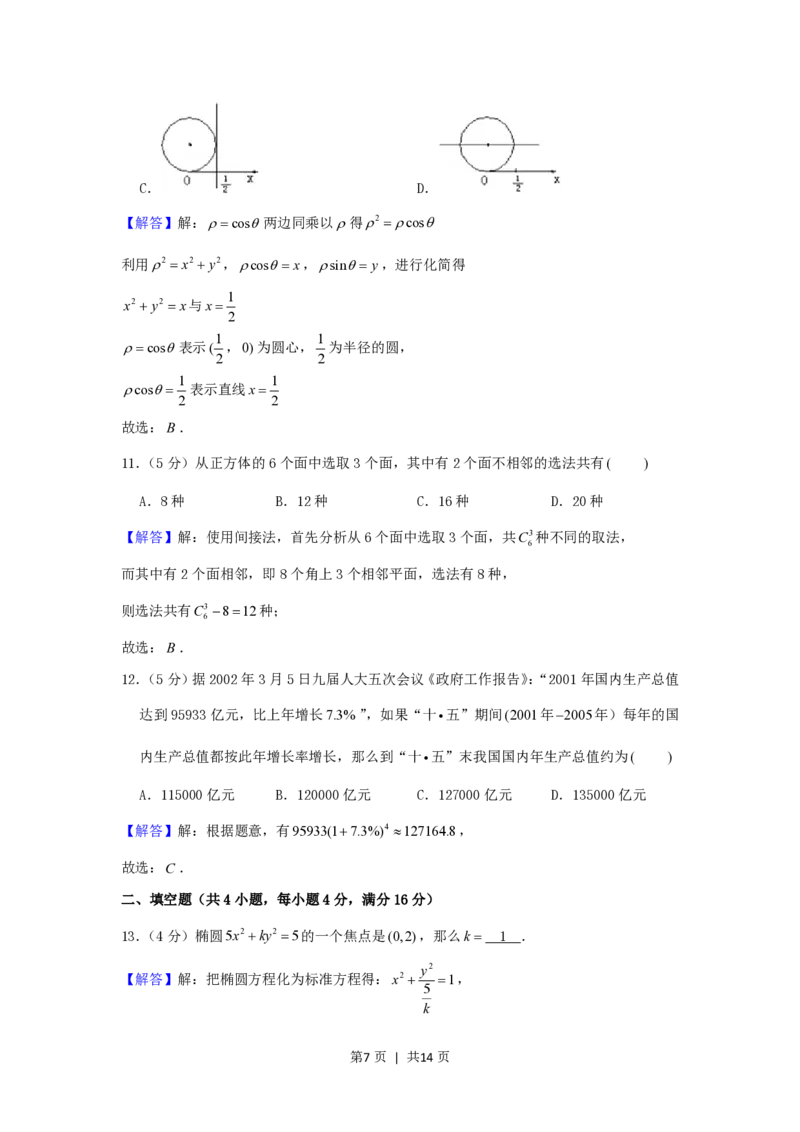10．（5分）极坐标方程cos与cos 的图形是( ) 2 A． B． C． D． 11．（5分）从正方体的6个面中选取3个面，其中有2个面不相邻的选法共有( ) A．8种 B．12种 C．16种 D．20种 12．（5分）据2002年3月5日九届人大五次会议《政府工作报告》：“2001年国内生产总值 达到95933亿元，比上年增长7.3%”，如果“十 五”期间(2001年2005年）每年的国  内生产总值都按此年增长率增长，那么到“十 五”末我国国内年生产总值约为( )  A．115000亿元 B．120000亿元 C．127000亿元 D．135000亿元 二、填空题（共4小题，每小题4分，满分16分） 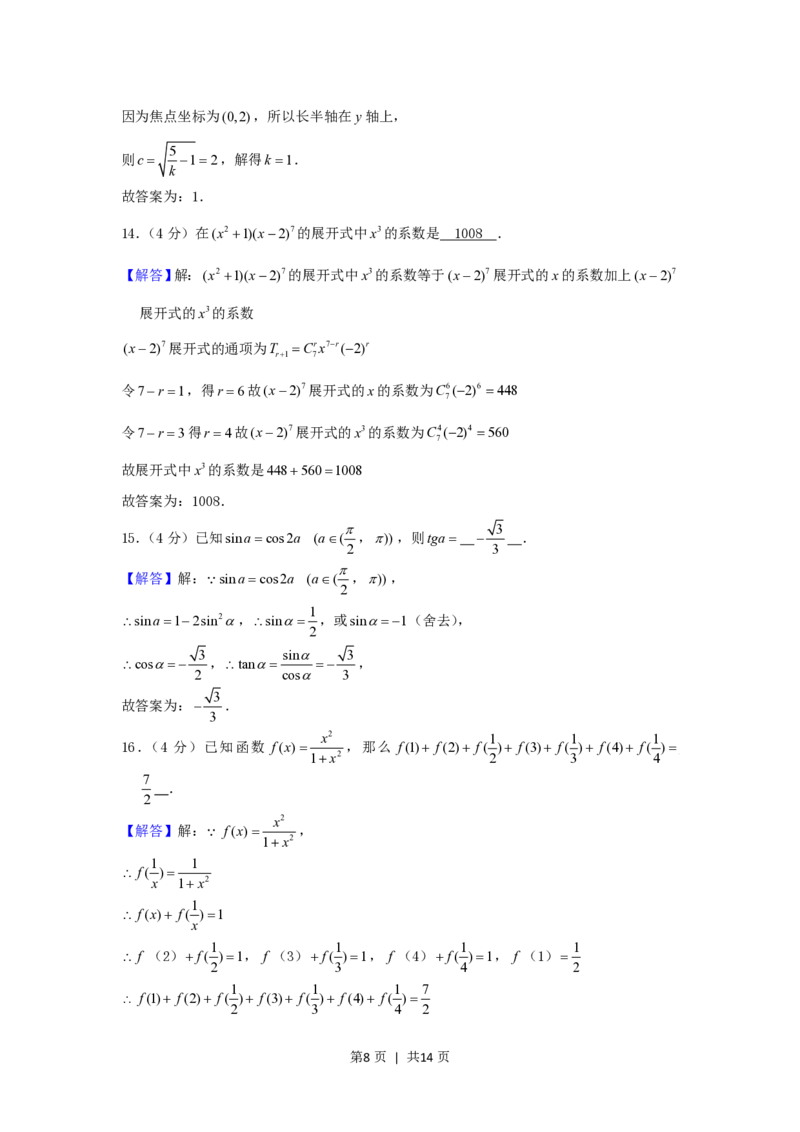13．（4分）椭圆5x2 ky2 5的一个焦点是(0,2)，那么k  ． 14．（4分）在(x2 1)(x2)7的展开式中x3的系数是 ．  15．（4分）已知sinacos2a (a( ，))，则tga ． 2 x2 1 1 1 16．（4分）已知函数 f(x) ，那么 f(1) f(2) f( ) f(3) f( ) f(4) f( ) ． 1x2 2 3 4 三、解答题（共6小题，满分74分） 17．（12分）已知复数z1i，求实数a，b使az2bz (a2z)2． 18．（12分）设{a }为等差数列，{b }为等比数列，a b 1，a a b ，bb a ，分 n n 1 1 2 4 3 2 4 3 别求出{a }及{b }的前10项的和S 及T ． n n 10 10 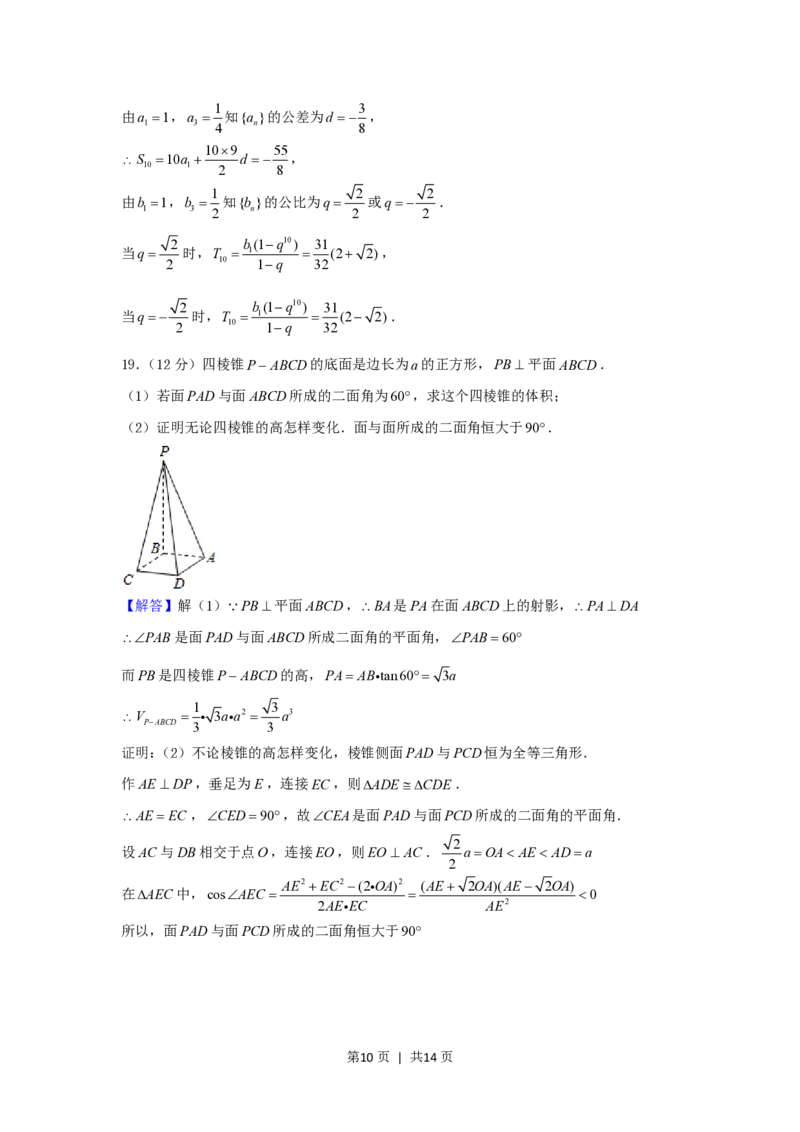19．（12分）四棱锥PABCD的底面是边长为a的正方形，PB平面ABCD． （1）若面PAD与面ABCD所成的二面角为60，求这个四棱锥的体积； 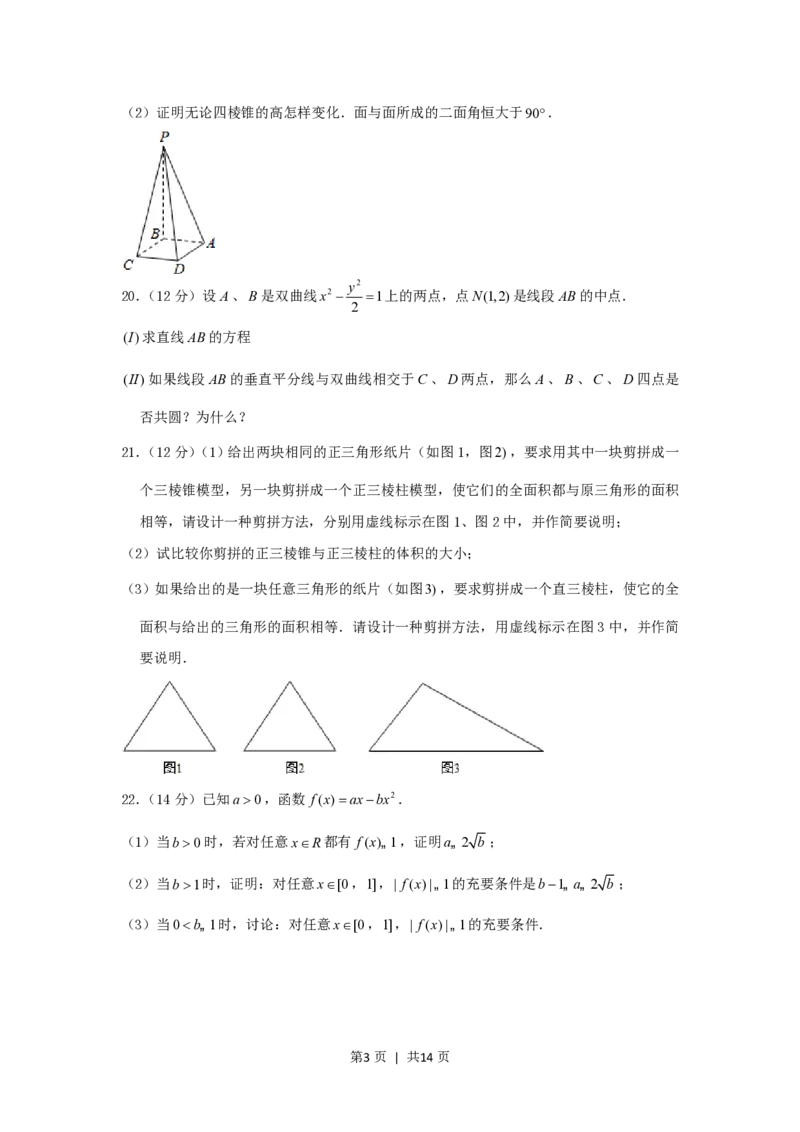第2页 | 共14页（2）证明无论四棱锥的高怎样变化．面与面所成的二面角恒大于90． y2 20．（12分）设A、B是双曲线x2  1上的两点，点N(1,2)是线段AB的中点． 2 (I)求直线AB的方程 (II)如果线段AB的垂直平分线与双曲线相交于C、D两点，那么A、B、C、D四点是 否共圆？为什么？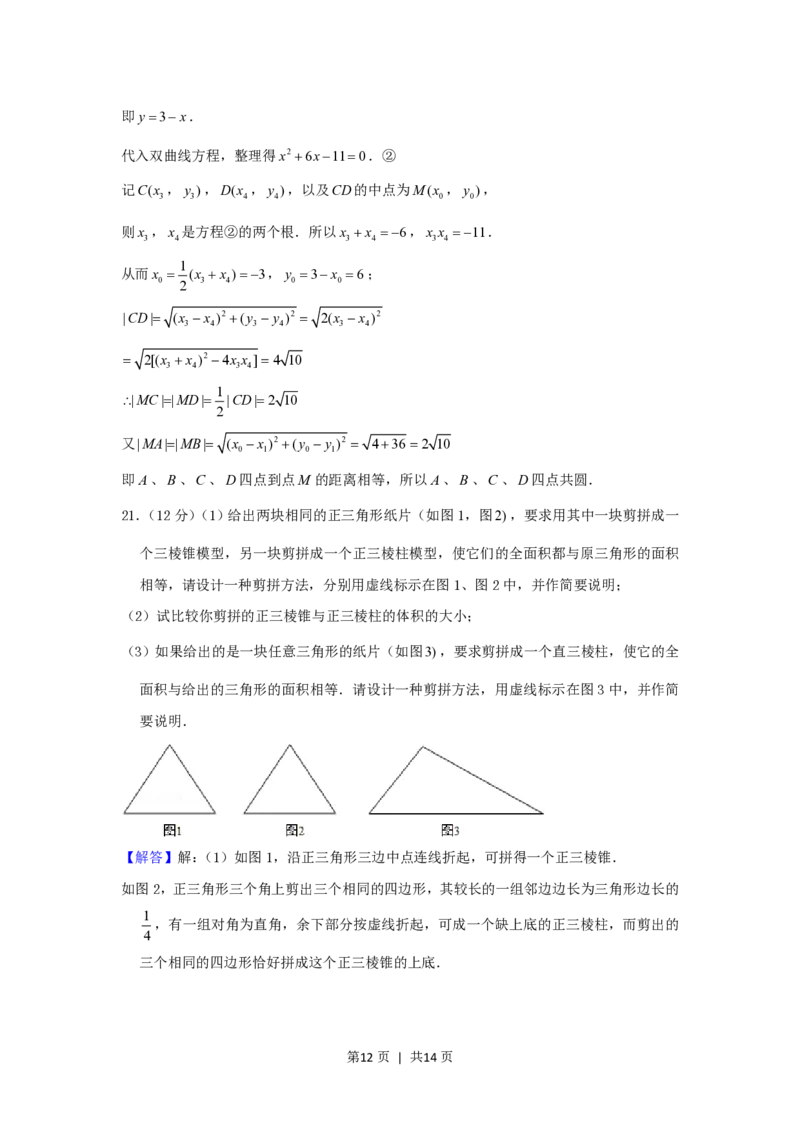 21．（12分）（1）给出两块相同的正三角形纸片（如图1，图2)，要求用其中一块剪拼成一 个三棱锥模型，另一块剪拼成一个正三棱柱模型，使它们的全面积都与原三角形的面积 相等，请设计一种剪拼方法，分别用虚线标示在图1、图2中，并作简要说明； （2）试比较你剪拼的正三棱锥与正三棱柱的体积的大小； （3）如果给出的是一块任意三角形的纸片（如图3)，要求剪拼成一个直三棱柱，使它的全 面积与给出的三角形的面积相等．请设计一种剪拼方法，用虚线标示在图3中，并作简 要说明． 22．（14分）已知a0，函数 f(x)axbx2． （1）当b0时，若对任意xR都有 f(x)„1，证明a„ 2 b ； （2）当b1时，证明：对任意x[0，1]，| f(x)|„1的充要条件是b1„ a„ 2 b ； （3）当0b„1时，讨论：对任意x[0，1]，| f(x)|„1的充要条件． 第3页 | 共14页参考答案 一、选择题（共12小题，每小题5分，满分60分） sin2x 1．（5分）函数 f(x) 的最小正周期是( ) cos2x  A． B． C．2 D．4 2 sin2x  【解答】解：函数 f(x) tan2x，所以函数的最小正周期为：T  cos2x 2 故选：A． 3 2．（5分）圆(x1)2  y2 1的圆心到直线y x的距离是( ) 3 1 3 A． B． C．1 D． 3 2 2 【解答】解：由(x1)2  y2 1得：圆心(1,0)， 所以根据点到直线的距离公式得： 3 3 | | 3 3 1 d    ． 3 2 3 2 ( )2 (1)2 3 3 故选：A． 3．（5分）不等式(1x)(1|x|)0的解集是( ) A．{x|0„ x1} B．{x|x0且x1} C．{x|1x1} D．{x|x1且 x1} 【解答】解：求不等式(1x)(1|x|)0的解集 则分两种情况讨论： 1x0 x1 情况1: 即： 1|x|0 1 X 1 则：1x1． 1x0 X 1 情况2: 即： 1|x|0  X 1或X 1 则：x1 两种情况取并集得{x|x1且x1}． 第4页 | 共14页故选：D． 4．（5分）在(0,2)内，使sinxcosx成立的x的取值范围是( )    5  A．( ， ) (， ) B．( ，) 4 2 4 4  5   5 3 C．( ， ) D．( ，) ( ， ) 4 4 4 4 2 【解答】解： sinxcosx，   sin(x )0， 4  2kx 2k (kZ)， 4 在(0,2)内，   5 x( , )， 4 4 故选：C． k  k  5．（5分）已知集合M {x|x  ，kZ}，N {x|x  ，kZ}，则( ) 2 4 4 2 A．M N B．M  N C．M  N D．M N   2k1 【解答】解：对于M 的元素，有x ，其分子为的奇数倍； 4 k2 对于N的元素，有x ，其分子为的整数倍； 4 分析易得，M  N； 故选：C． 6．（5分）一个圆锥和一个半球有公共底面，如果圆锥的体积与半球的体积恰好相等，则圆 锥轴截面顶角的余弦值是( ) 3 4 3 3 A． B． C． D． 4 3 5 5 【解答】解：设圆锥的半径为R，高为H ，母线与轴所成角为，则圆锥的高H R ctg  1 1 圆锥的体积V  R2 H  R3ctg 1 3  3 2 半球的体积V  R3 2 3 1 2 V V 即： R3ctg R3  1 2 3 3 ctg2 第5页 | 共14页3 cos2 5 故选：D． 7．（5分）函数 f(x)x|xa|b是奇函数的充要条件是( ) A．ab0 B．ab0 C．ab D．a2 b2 0 【解答】解：根据奇函数的定义可知 f(x)x|ax|bf(x)x|xa|b对任意x恒成立 a0，b0，故选D 8．（5分）已知0x ya1，则有( ) A．log (xy)0 B．0log (xy)1 C．1log (xy)2 D．log (xy)2 a a a a 【解答】解： 0x ya1log xlog a1，log ylog a1  a a a a log (xy)log xlog y2 a a a 故选：D． 1 9．（5分）函数y1 ( ) x1 A．在(1,)内单调递增 B．在(1,)内单调递减 C．在(1,)内单调递增 D．在(1,)内单调递减 1 1 【解答】解：y 是y 向右平移1个单位而得到， x1 x 1 故y1 在(1,)上为增函数， x1 在(,1)上为增函数． 故选：C． 1 10．（5分）极坐标方程cos与cos 的图形是( ) 2 A． B． 第6页 | 共14页C． D． 【解答】解：cos两边同乘以得2 cos 利用2 x2  y2，cosx，sin y，进行化简得 1 x2  y2 x与x 2 1 1 cos表示( ，0)为圆心， 为半径的圆， 2 2 1 1 cos 表示直线x 2 2 故选：B． 11．（5分）从正方体的6个面中选取3个面，其中有2个面不相邻的选法共有( ) A．8种 B．12种 C．16种 D．20种 【解答】解：使用间接法，首先分析从6个面中选取3个面，共C3种不同的取法， 6 而其中有2个面相邻，即8个角上3个相邻平面，选法有8种， 则选法共有C3 812种； 6 故选：B． 12．（5分）据2002年3月5日九届人大五次会议《政府工作报告》：“2001年国内生产总值 达到95933亿元，比上年增长7.3%”，如果“十 五”期间(2001年2005年）每年的国  内生产总值都按此年增长率增长，那么到“十 五”末我国国内年生产总值约为( )  A．115000亿元 B．120000亿元 C．127000亿元 D．135000亿元 【解答】解：根据题意，有95933(17.3%)4 127164.8， 故选：C． 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）椭圆5x2 ky2 5的一个焦点是(0,2)，那么k  1 ． y2 【解答】解：把椭圆方程化为标准方程得：x2  1， 5 k 第7页 | 共14页因为焦点坐标为(0,2)，所以长半轴在y轴上， 5 则c 12，解得k 1． k 故答案为：1． 14．（4分）在(x2 1)(x2)7的展开式中x3的系数是 1008 ． 【解答】解：(x2 1)(x2)7的展开式中x3的系数等于(x2)7展开式的x的系数加上(x2)7 展开式的x3的系数 (x2)7展开式的通项为T Crx7r(2)r r1 7 令7r 1，得r 6故(x2)7展开式的x的系数为C6(2)6 448 7 令7r 3得r 4故(x2)7展开式的x3的系数为C4(2)4 560 7 故展开式中x3的系数是4485601008 故答案为：1008．  3 15．（4分）已知sinacos2a (a( ，))，则tga  ． 2 3  【解答】解： sinacos2a (a( ，))，  2 1 sina12sin2，sin ，或sin1（舍去）， 2 3 sin 3 cos ，tan  ， 2 cos 3 3 故答案为： ． 3 x2 1 1 1 16．（4 分）已知函数 f(x) ，那么 f(1) f(2) f( ) f(3) f( ) f(4) f( ) 1x2 2 3 4 7 ． 2 x2 【解答】解： f(x) ，  1x2 1 1 f( ) x 1x2 1 f(x) f( )1 x 1 1 1 1 f （2）f( )1， f （3）f( )1， f （4）f( )1， f （1） 2 3 4 2 1 1 1 7  f(1) f(2) f( ) f(3) f( ) f(4) f( ) 2 3 4 2 第8页 | 共14页7 故答案为： 2 三、解答题（共6小题，满分74分） 17．（12分）已知复数z1i，求实数a，b使az2bz (a2z)2． 【解答】解： z1i，  az2bz (a2b)(a2b)i(a2z)2 (a2)2 44(a2)i (a2 4a)4(a2)i 因为a，b都是实数， 所以由az2bz (a2z)2 a2ba2 4a 得 a2b4(a2) 两式相加，整理得 a2 6a80 解得a 2，a 4 1 2 对应得b 1，b 2 1 2 所求实数为a2，b1或a4，b2 18．（12分）设{a }为等差数列，{b }为等比数列，a b 1，a a b ，bb a ，分 n n 1 1 2 4 3 2 4 3 别求出{a }及{b }的前10项的和S 及T ． n n 10 10 【解答】解： {a }为等差数列，{b }为等比数列，  n n a a 2a ，bb b2 2 4 3 2 4 3 已知a a b ，bb a ， 2 4 3 2 4 3 b 2a ，a b2 3 3 3 3 得b 2b2 3 3 1 1 b 0b  ,a   3 3 2 3 4 第9页 | 共14页1 3 由a 1，a  知{a }的公差为d  ， 1 3 4 n 8 109 55 S 10a  d  ， 10 1 2 8 1 2 2 由b 1，b  知{b }的公比为q 或q ． 1 3 2 n 2 2 2 b(1q10) 31 当q 时，T  1  (2 2)， 2 10 1q 32 2 b(1q10) 31 当q 时，T  1  (2 2)． 2 10 1q 32 19．（12分）四棱锥PABCD的底面是边长为a的正方形，PB平面ABCD． （1）若面PAD与面ABCD所成的二面角为60，求这个四棱锥的体积； （2）证明无论四棱锥的高怎样变化．面与面所成的二面角恒大于90． 【解答】解（1） PB平面ABCD，BA是PA在面ABCD上的射影，PADA  PAB是面PAD与面ABCD所成二面角的平面角，PAB60 而PB是四棱锥PABCD的高，PA AB tan60 3a  1 3 V  3a a2  a3 PABCD 3   3 证明：（2）不论棱锥的高怎样变化，棱锥侧面PAD与PCD恒为全等三角形． 作AE DP，垂足为E，连接EC，则ADECDE． AEEC ，CED90，故CEA是面PAD与面PCD所成的二面角的平面角． 2 设AC与DB相交于点O，连接EO，则EO AC． aOA AE ADa 2 AE2 EC2 (2 OA)2 (AE 2OA)(AE 2OA) 在AEC 中，cosAEC    0 2AE EC AE2  所以，面PAD与面PCD所成的二面角恒大于90 第10页 | 共14页y2 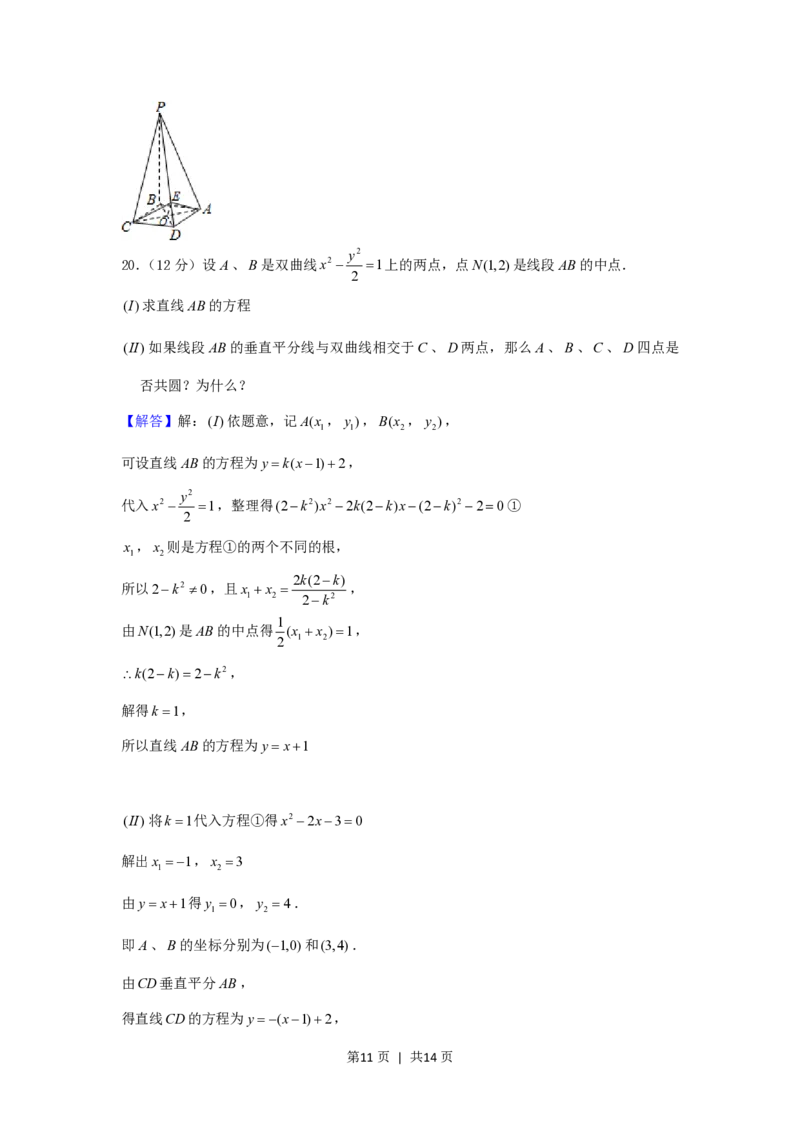20．（12分）设A、B是双曲线x2  1上的两点，点N(1,2)是线段AB的中点． 2 (I)求直线AB的方程 (II)如果线段AB的垂直平分线与双曲线相交于C、D两点，那么A、B、C、D四点是 否共圆？为什么？ 【解答】解：(I)依题意，记A(x ，y )，B(x ，y )， 1 1 2 2 可设直线AB的方程为yk(x1)2， y2 代入x2  1，整理得(2k2)x2 2k(2k)x(2k)2 20① 2 x ，x 则是方程①的两个不同的根， 1 2 2k(2k) 所以2k2 0，且x x  ， 1 2 2k2 1 由N(1,2)是AB的中点得 (x x )1， 2 1 2 k(2k)2k2， 解得k 1， 所以直线AB的方程为yx1 (II)将k 1代入方程①得x2 2x30 解出x 1，x 3 1 2 由yx1得y 0，y 4． 1 2 即A、B的坐标分别为(1,0)和(3,4)． 由CD垂直平分AB， 得直线CD的方程为y(x1)2， 第11页 | 共14页即y3x． 代入双曲线方程，整理得x2 6x110．② 记C(x ，y )，D(x ，y )，以及CD的中点为M(x ，y )， 3 3 4 4 0 0 则x ，x 是方程②的两个根．所以x x 6，x x 11． 3 4 3 4 3 4 1 从而x  (x x )3，y 3x 6； 0 2 3 4 0 0 |CD| (x x )2 (y  y )2  2(x x )2 3 4 3 4 3 4  2[(x x )2 4x x ]4 10 3 4 3 4 1 |MC||MD| |CD|2 10 2 又|MA||MB| (x x )2 (y  y )2  436 2 10 0 1 0 1 即A、B、C、D四点到点M 的距离相等，所以A、B、C、D四点共圆． 21．（12分）（1）给出两块相同的正三角形纸片（如图1，图2)，要求用其中一块剪拼成一 个三棱锥模型，另一块剪拼成一个正三棱柱模型，使它们的全面积都与原三角形的面积 相等，请设计一种剪拼方法，分别用虚线标示在图1、图2中，并作简要说明； （2）试比较你剪拼的正三棱锥与正三棱柱的体积的大小； （3）如果给出的是一块任意三角形的纸片（如图3)，要求剪拼成一个直三棱柱，使它的全 面积与给出的三角形的面积相等．请设计一种剪拼方法，用虚线标示在图3中，并作简 要说明． 【解答】解：（1）如图1，沿正三角形三边中点连线折起，可拼得一个正三棱锥． 如图2，正三角形三个角上剪出三个相同的四边形，其较长的一组邻边边长为三角形边长的 1 ，有一组对角为直角，余下部分按虚线折起，可成一个缺上底的正三棱柱，而剪出的 4 三个相同的四边形恰好拼成这个正三棱锥的上底． 第12页 | 共14页（2）依上面剪拼方法，有V V ． 柱 锥 推理如下： 设给出正三角形纸片的边长为2， 3 那么，正三棱锥与正三棱柱的底面都是边长为1的正三角形，其面积为 ． 4 2 2 3 6 现 在 计 算 它 们 的 高 ： h  1    ， 锥 3 2  3   1 3  1  3  3 6 3 32 2 h 柱  2 tan30 6 ．V 柱 V 锥   h 柱  3 h 锥    4    6  9     4  24 0 所以V V ． 柱 锥 （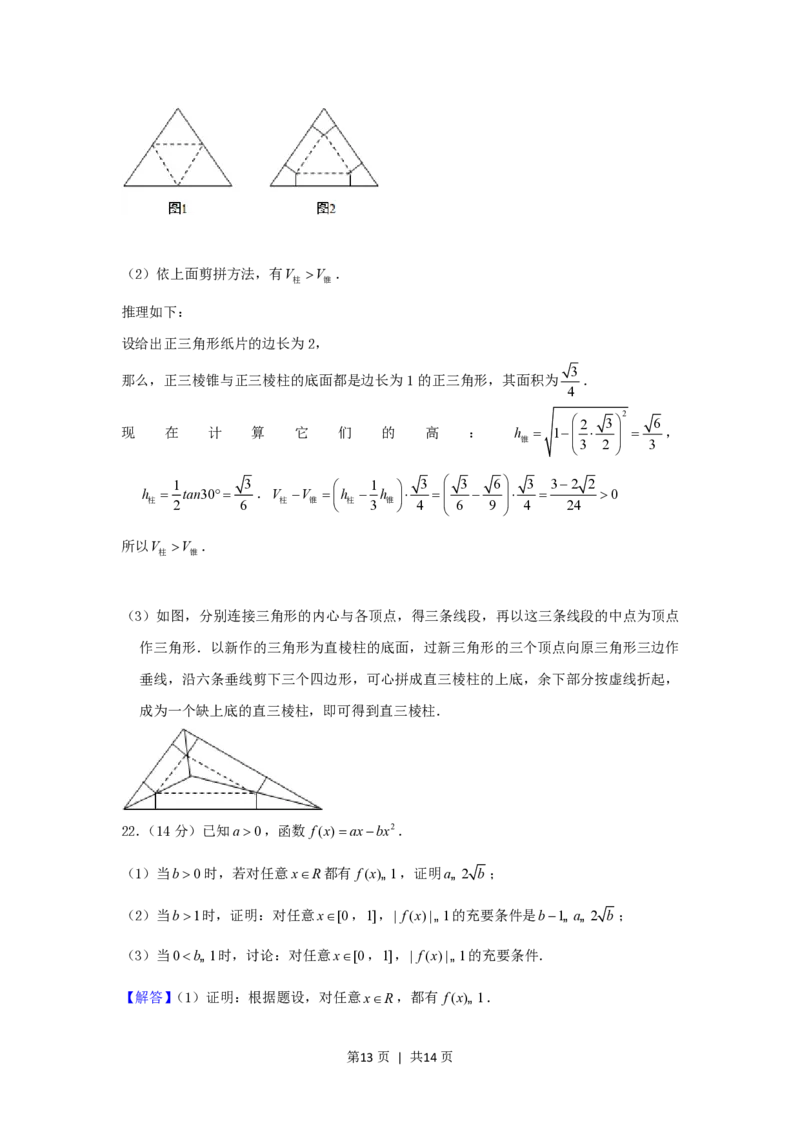3）如图，分别连接三角形的内心与各顶点，得三条线段，再以这三条线段的中点为顶点 作三角形．以新作的三角形为直棱柱的底面，过新三角形的三个顶点向原三角形三边作 垂线，沿六条垂线剪下三个四边形，可心拼成直三棱柱的上底，余下部分按虚线折起， 成为一个缺上底的直三棱柱，即可得到直三棱柱． 22．（14分）已知a0，函数 f(x)axbx2． （1）当b0时，若对任意xR都有 f(x)„1，证明a„ 2 b ； （2）当b1时，证明：对任意x[0，1]，| f(x)|„1的充要条件是b1„ a„ 2 b ； （3）当0b„1时，讨论：对任意x[0，1]，| f(x)|„1的充要条件． 【解答】（1）证明：根据题设，对任意xR，都有 f(x)„1． 第13页 | 共14页a a2 a a2 又 f(x)b(x )2  ．f( ) „1， 2b 4b 2b 4b a0，b0，  a„ 2 b． （2）证明：必要性：对任意x[0，1]，| f(x)|„1 f(x)… 1． 据此可推出 f （1）… 1，即ab… 1， a…b1． 对任意x[0，1]，| f(x)|„1 f(x)„1， 1 1 1 因为b1，可得0 1，可推出 f( )„1，即a 1„1，  b b b a„ 2 b， b1„ a„ 2 b． 充分性：因为b1，a…b1，对任意x[0，1]， 可以推出axbx2…b(xx2)x… x… 1，即axbx2… 1， 因为b1，a„ 2 b 对任意x[0，1]， 1 可以推出：2 bbx2„ b(x )2 1„1，即axbx2„1， b 1„ f(x)„1． 综上，当b1时，对任意x[0，1]，| f(x)|„1的充要条件是b1„ a„ 2 b ． （3）解：因为 a0， 0b„1时，对任意 x[0，1]有 f(x)axbx2… b… 1，即 f(x)… 1； f(x)„1 f （1）„1ab„1，即a„ b1， 又a„ b1 f(x)„ (b1)xbx2„1，即 f(x)„1． 所以，当a0，0b„1时，对任意x[0，1]，| f(x)|„1的充要条件是a„ b1． 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/5/27 22:57:29；用户：15217760367；邮箱：15217760367；学号：10888156 第14页 | 共14页