文档内容
完成时间: 月 日 天气:
作业 06 平面向量基本定理
及爪子定理、等和线(系数和)的应用
1.平面向量基本定理
如果e ,e 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一
1 2
对实数λ ,λ ,使a=λ e +λ e .
1 2 1 1 2 2
其中,不共线的向量e ,e 叫做表示这一平面内所有向量的一组基底.
1 2
(1).基底e ,e 必须是同一平面内的两个不共线向量,零向量不能作为基底.
1 2
(2)基底给定,同一向量的分解形式唯一.
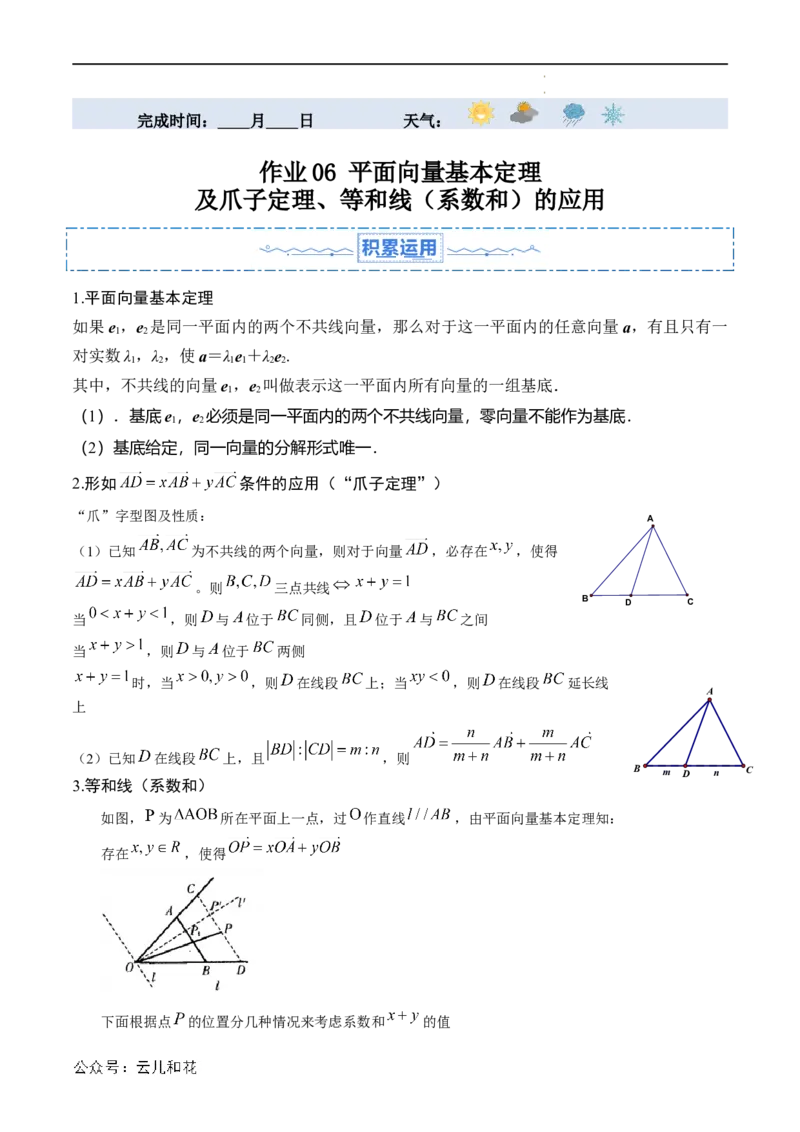
2.形如 条件的应用(“爪子定理”)
“爪”字型图及性质:
A
(1)已知 为不共线的两个向量,则对于向量 ,必存在 ,使得
。则 三点共线
B D C
当 ,则 与 位于 同侧,且 位于 与 之间
当 ,则 与 位于 两侧
时,当 ,则 在线段 上;当 ,则 在线段 延长线
A
上
(2)已知 在线段 上,且 ,则
B m D n C
3.等和线(系数和)
如图, 为 所在平面上一点,过 作直线 ,由平面向量基本定理知:
存在 ,使得
下面根据点 的位置分几种情况来考虑系数和 的值
学科网(北京)股份有限公司①若 时,则射线 与 无交点,由 知,存在实数 ,使得
而 ,所以 ,于是
②若 时,
(i)如图1,当 在 右侧时,过 作 ,交射线 于 两点,则
,不妨设 与 的相似比为
由 三点共线可知:存在 使得:
所以
(ii)当 在 左侧时,射线 的反向延长线与 有交点,如图1作 关于 的对称点 ,由
(i)的分析知:存在存在 使得:
所以
于是
综合上面的讨论可知:图中 用 线性表示时,其系数和 只与两三角形的相似比有关。
我们知道相似比可以通过对应高线、中线、角平分线、截线、外接圆半径、内切圆半径之比来刻画。
因为三角形的高线相对比较容易把握,我们不妨用高线来刻画相似比,在图中,过 作 边的垂线 ,
设点 在 上的射影为 ,直线 交直线 于点 ,则 ( 的符号由点 的位置确定),因
此只需求出 的范围便知 的范围
一、单选题
1.设D为 ABC所在平面内一点 ,则( )
A. B.
C. D.
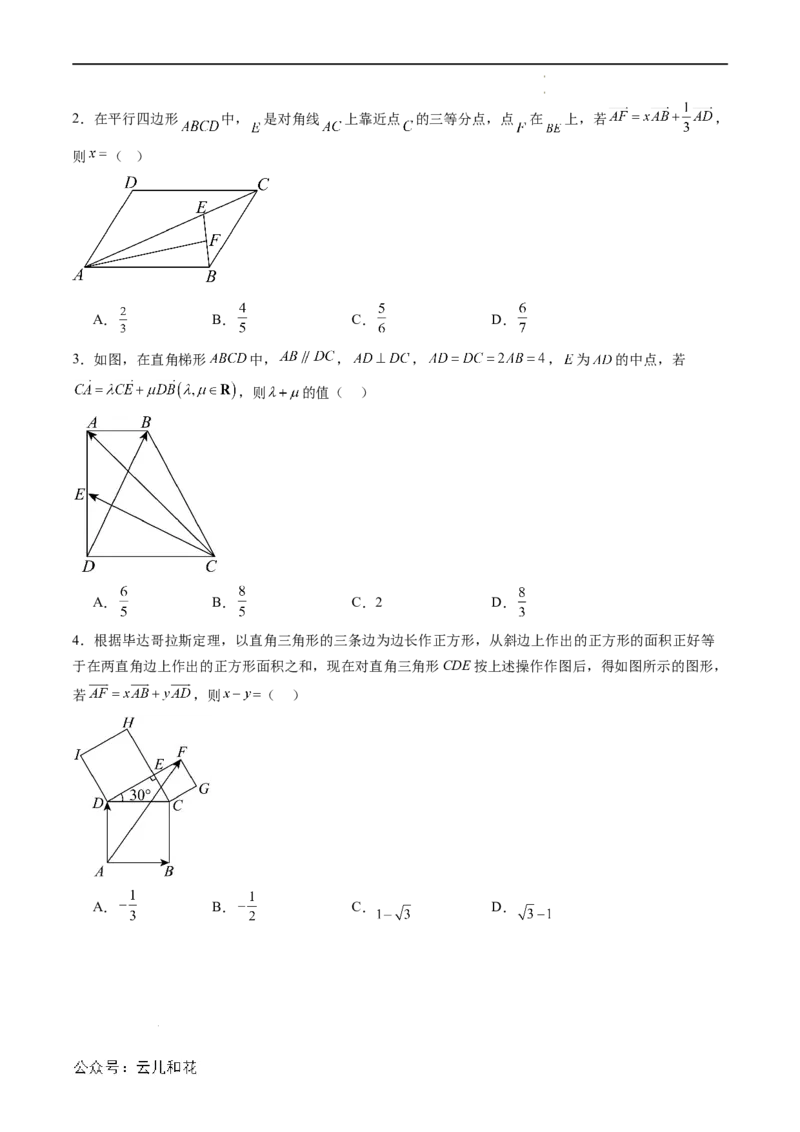
学科网(北京)股份有限公司2.在平行四边形 中, 是对角线 上靠近点 的三等分点,点 在 上,若 ,
则 ( )
A. B. C. D.
3.如图,在直角梯形 中, , , , 为 的中点,若
,则 的值( )
A. B. C.2 D.
4.根据毕达哥拉斯定理,以直角三角形的三条边为边长作正方形,从斜边上作出的正方形的面积正好等
于在两直角边上作出的正方形面积之和,现在对直角三角形CDE按上述操作作图后,得如图所示的图形,
若 ,则 =( )
A. B. C. D.
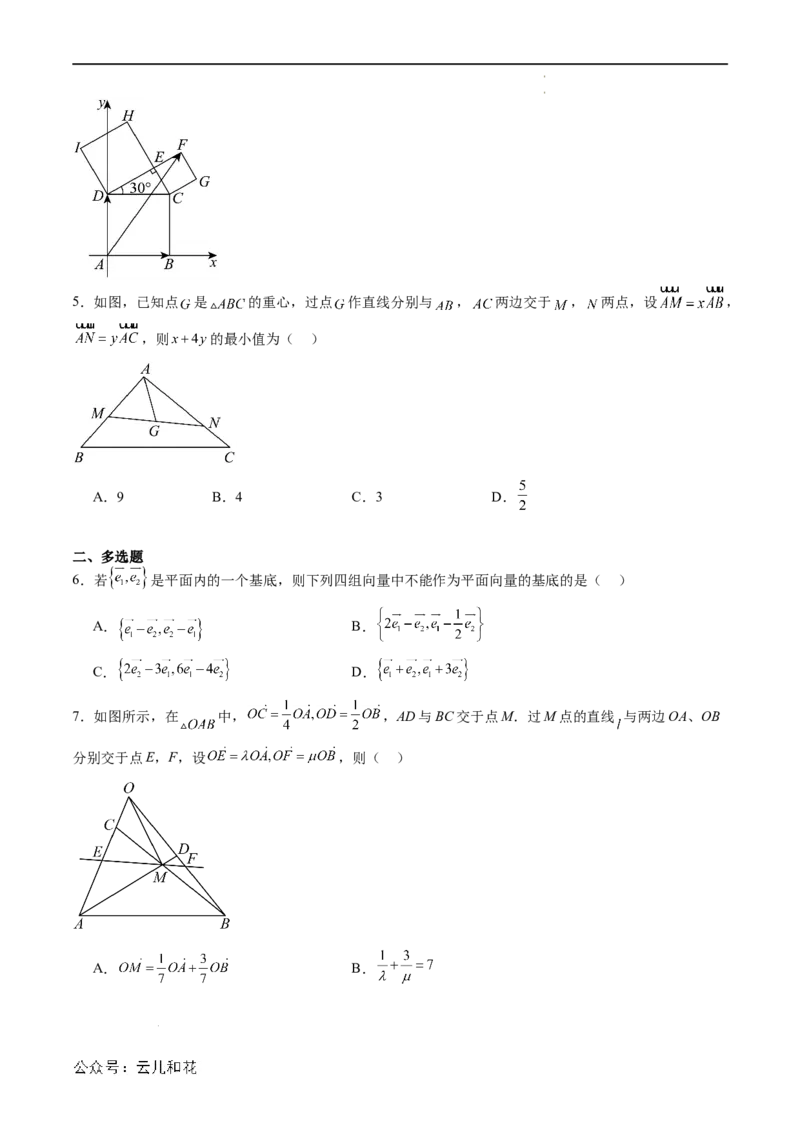
学科网(北京)股份有限公司5.如图,已知点 是 的重心,过点 作直线分别与 , 两边交于 , 两点,设 ,
,则 的最小值为( )
A.9 B.4 C.3 D.
二、多选题
6.若 是平面内的一个基底,则下列四组向量中不能作为平面向量的基底的是( )
A. B.
C. D.
7.如图所示,在 中, ,AD与BC交于点M.过M点的直线 与两边OA、OB
分别交于点E,F,设 ,则( )
A. B.
学科网(北京)股份有限公司C. 可能的取值为 D. 的最小值为
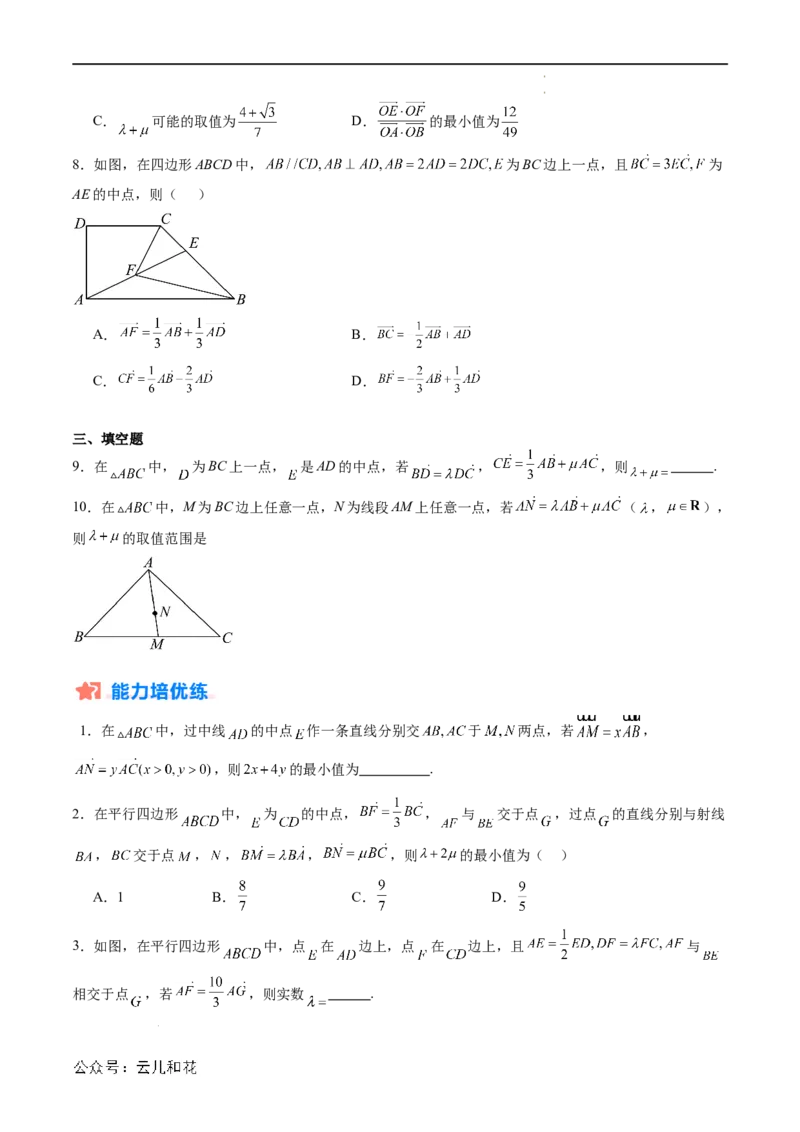
8.如图,在四边形ABCD中, 为BC边上一点,且 为
AE的中点,则( )
A. B.
C. D.
三、填空题
9.在 中, 为BC上一点, 是AD的中点,若 , ,则 .
10.在 中,M为BC边上任意一点,N为线段AM上任意一点,若 ( , ),
则 的取值范围是
1.在 中,过中线 的中点 作一条直线分别交 于 两点,若 ,
,则 的最小值为 .
2.在平行四边形 中, 为 的中点, , 与 交于点 ,过点 的直线分别与射线
, 交于点 , , , ,则 的最小值为( )
A.1 B. C. D.
3.如图,在平行四边形 中,点 在 边上,点 在 边上,且 与
相交于点 ,若 ,则实数 .
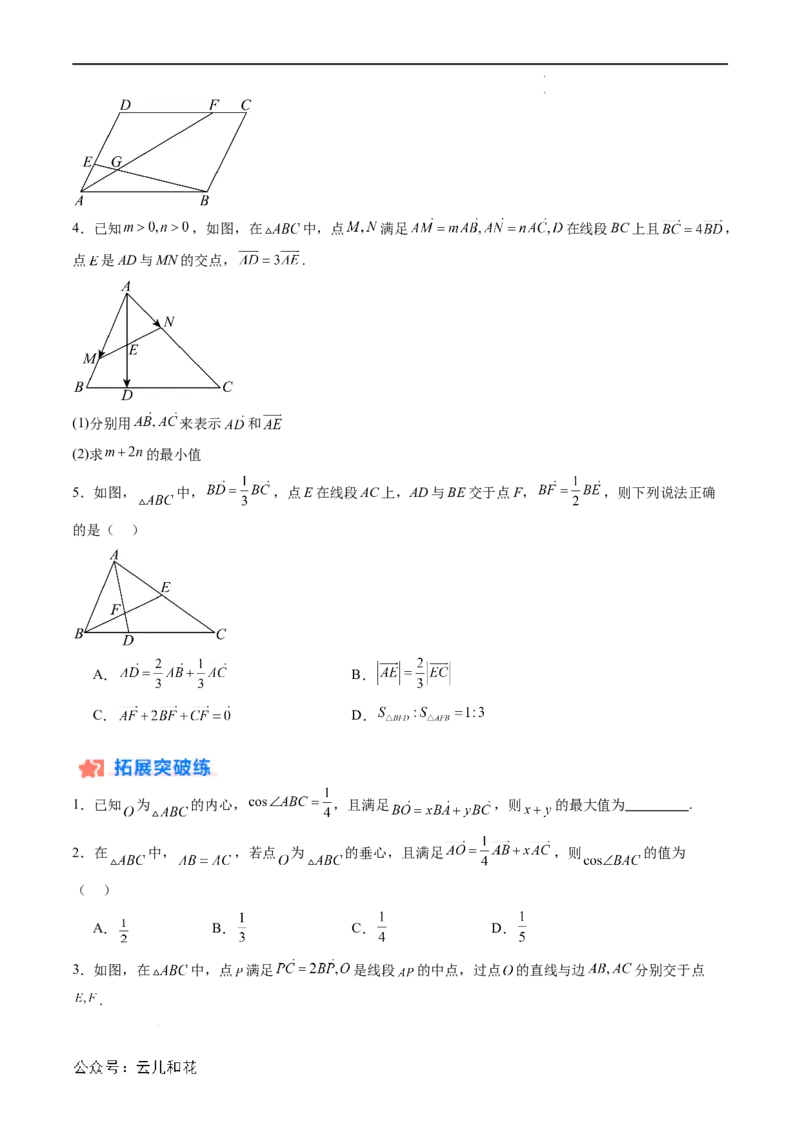
学科网(北京)股份有限公司4.已知 ,如图,在 中,点 满足 在线段BC上且 ,
点 是AD与MN的交点, .
(1)分别用 来表示 和
(2)求 的最小值
5.如图, 中, ,点E在线段AC上,AD与BE交于点F, ,则下列说法正确
的是( )
A. B.
C. D.
1.已知 为 的内心, ,且满足 ,则 的最大值为 .
2.在 中, ,若点 为 的垂心,且满足 ,则 的值为
( )
A. B. C. D.
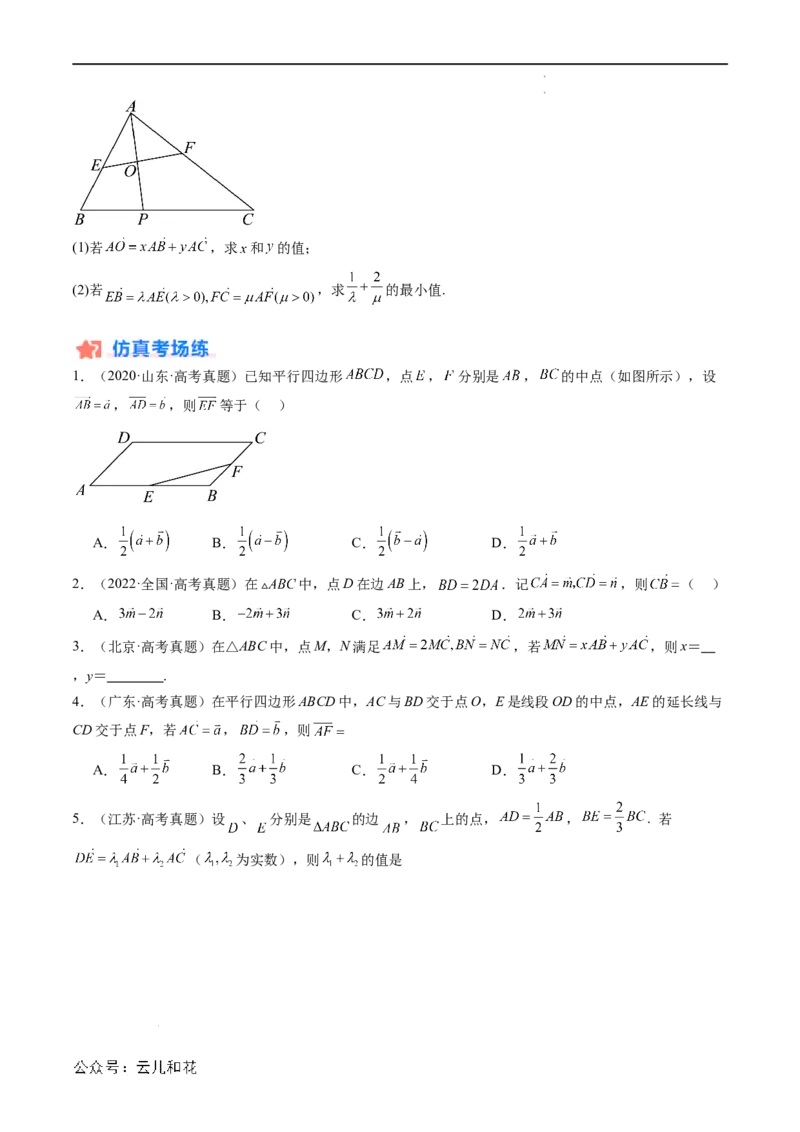
3.如图,在 中,点 满足 是线段 的中点,过点 的直线与边 分别交于点
.
学科网(北京)股份有限公司(1)若 ,求 和 的值;
(2)若 ,求 的最小值.
1.(2020·山东·高考真题)已知平行四边形 ,点 , 分别是 , 的中点(如图所示),设
, ,则 等于( )
A. B. C. D.
2.(2022·全国·高考真题)在 中,点D在边AB上, .记 ,则 ( )
A. B. C. D.
3.(北京·高考真题)在△ABC中,点M,N满足 ,若 ,则x=
,y= .
4.(广东·高考真题)在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与
CD交于点F,若 , ,则
A. B. C. D.
5.(江苏·高考真题)设 、 分别是 的边 , 上的点, , . 若
( 为实数),则 的值是
学科网(北京)股份有限公司