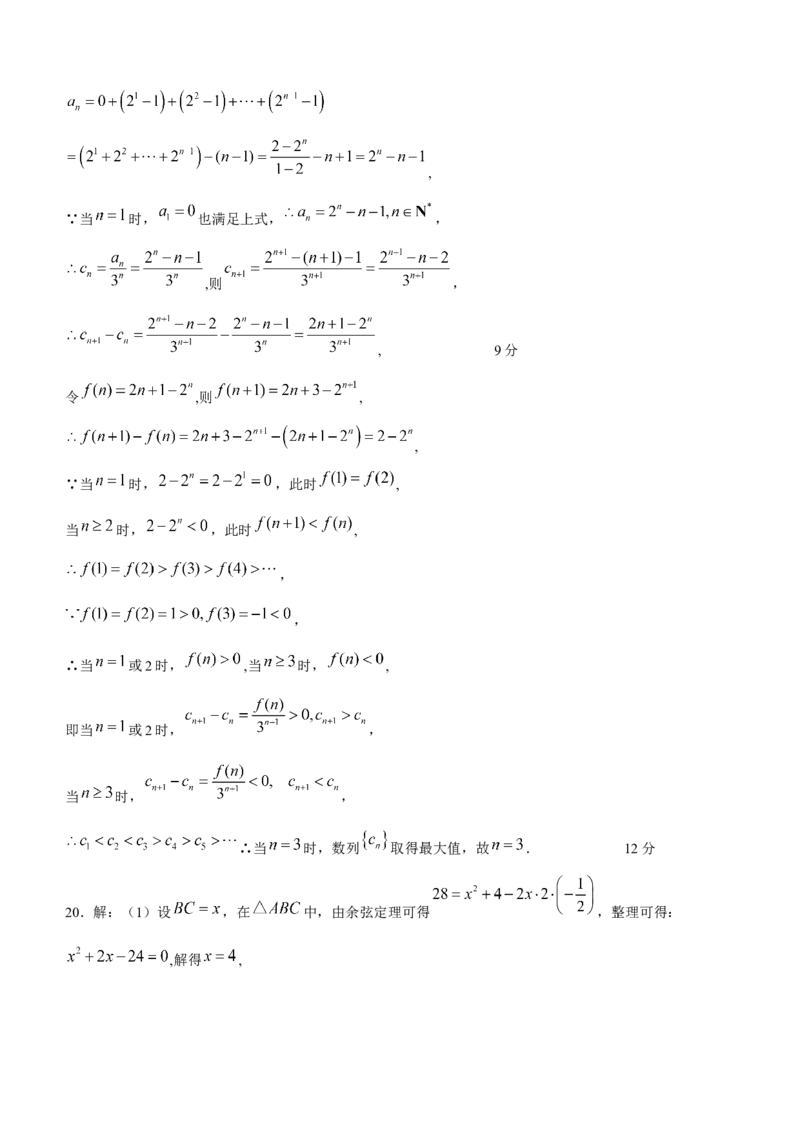河南省信阳市信阳高级中学2023—2024学年高三上学期第一次模拟数学答案(1)_2023年11月_01每日更新_23号_2024届河南省信阳市信阳高级中学高三上学期第一次模拟

河南省信阳高级中学 2023-2024 学年高三上期 11 月一模 数学答案 一、选择题： 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C D A C D C D D AC AC ABC ABD 8．因为 ， 所以 ；令 ,所以 在 上单调递增， 因为 ，所以 ,即 , 所以 ． 所以 ；同理 ，所以 ,即 ,也即 , 所以 ,所以 ． 综上， ,故选：D． 11．解：对于A, 为 中点， ,∴四边形 为平行四边形， 又 ,∴四边形 为矩形， ； ， ,又 平面 , 平面 ,A正确； 对于B, ,即 平面 平面 , ,又 平面 平面 ； ∵矩形 的外接圆半径 ，∴四棱锥 的外接球半径，∴四棱锥 外接球的体积 ，B正确；对 于C, 平面 平面 ， ；又 ,∴二面角 的平面角为 , ，∴二面角 的大小为 ,C正确； 对于D, 平面 即为直线 与平面 所成角， ， ，即直线直线 与平面 所成角的正切值为 ，D错误． 故选：ABC． 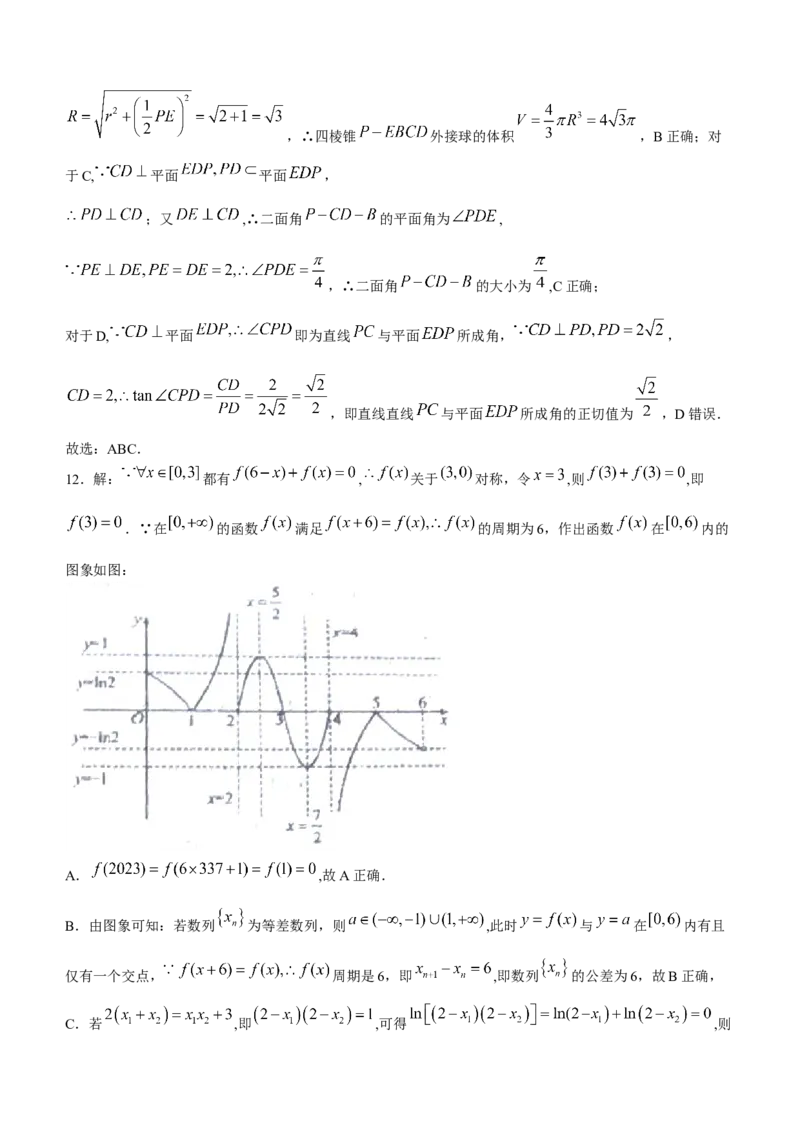12．解： 都有 , 关于 对称，令 ,则 ,即 ．∵在 的函数 满足 的周期为6，作出函数 在 内的 图象如图： A． ,故A正确． B．由图象可知：若数列 为等差数列，则 ,此时 与 在 内有且 仅有一个交点， 周期是6，即 ,即数列 的公差为6，故B正确， C．若 ,即 ,可得 ,则,即 与 在 内有且仅有2个交点，结合图象可得 ，故 C错误； D．若 ,则 与 在 内有且仅有3个交点，且 ,则 ,∴数列 是以7为 首项，公差 的等差数列，可得 , ,故D正确．故选：ABD． 二、填空题： 13．2 14． 15． 16．1 16．解：因为 , 所以 为 上的奇函数， 又 ， 所以 在 上单调递增． 因为 对任意的 恒成立， 所以 对任意的 恒成立， 所以 对任意的 恒成立， 即 对任意的 恒成立．令 ,所以 , 所以当 时， 在 上为增函数； 当 时， 在 上为减函数．所以 ,设 ,显然 为 上的增函数，因为 ，所以存在 ，使得 ,所以 ,此时 , 所以 ，即 的最大值为1．故答案为：1． 三、解答题 17．解：（1）由 得 , 令 ,得 , 当 时，原不等式的解集为 ； 当 时，原不等式的解集为 ； 当 时，原不等式的解集为 ． （5分） （2）由 即 在 上恒成立， 得 令 ， 则 ． 故实数 的取值范围是 10分 18．解：（1）由题意得 ，∴最小正周期 ，则 ， ．若选①， 为奇函数，则 ， ，即 ， ，即 ， ，即 ，． 若选②，当 时 ，即 ， ． 若选③， 是函数 的一条对称轴， ，即 ， ． 6分 （2） ，即 ， 即 ，即 ， 又 的面积 得 ， 在 中，由余弦定理得 ，解得 ． 12分 19．（1）证明：由题意，当 时， , 则 ,又 ， ∴数列 是以2为首项，2为公比的等比数列．5分 （2）解：由（1）可知， ,则 ， 即 ,各项相加，可得, ∵当 时， 也满足上式， ， ,则 ， , 9分 令 ,则 , , ∵当 时， ，此时 , 当 时， ，此时 , ， ， ∴当 或2时， ,当 时， , 即当 或2时， ， 当 时， ， ∴当 时，数列 取得最大值，故 ． 12分 20．解：（1）设 ，在 中，由余弦定理可得 ，整理可得： ,解得 ,所以 ，则 ，因为 ，所以 ，所以 ； 5分 （2）设 ,则 ， 在 中，由正弦定理可得 ， 在 中，由正弦定理可得 ， 两式相除可得 ，展开可得 ，所以可得 , 即 ,解得 或 ， 又因为 ，所以 ，即 ． 12分 21．（1）证明：取 的中点 ,连接 , 分别是 的中点， 且 ； 且 ； ．又 平面 平面 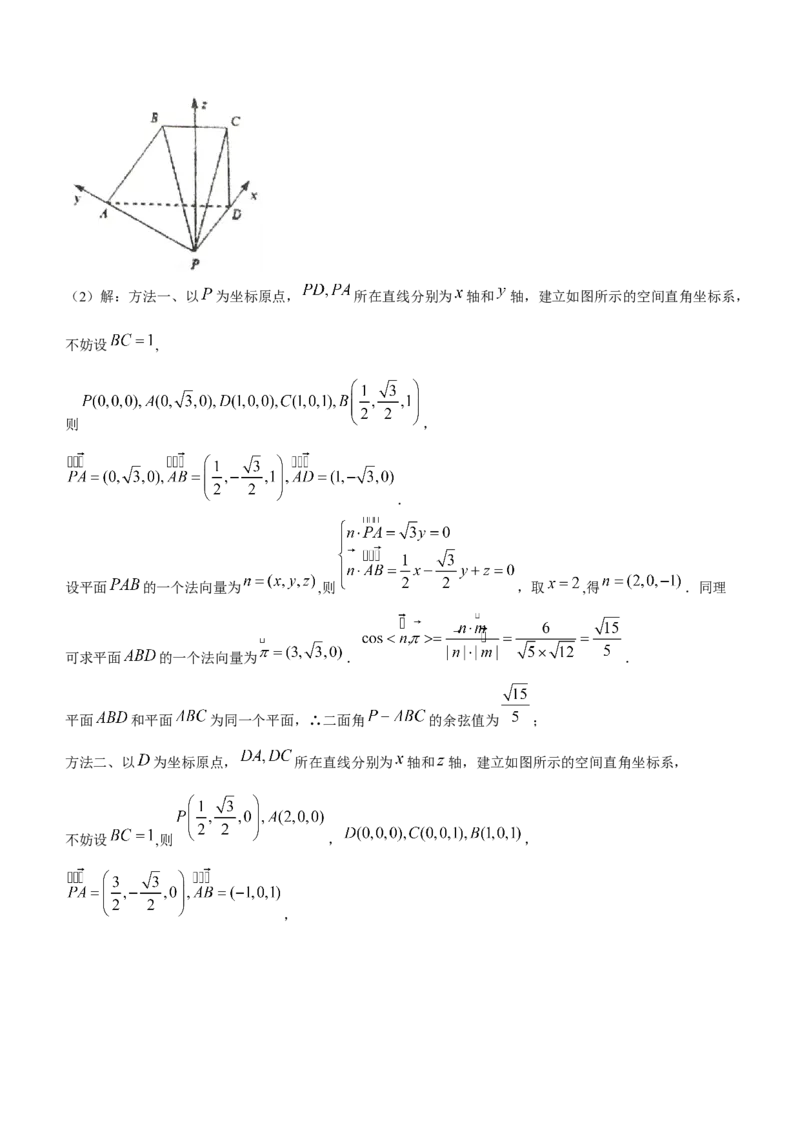平面 ； 5分（2）解：方法一、以 为坐标原点， 所在直线分别为 轴和 轴，建立如图所示的空间直角坐标系， 不妨设 , 则 ， ． 设平面 的一个法向量为 ,则 ，取 ,得 ．同理 可求平面 的一个法向量为 ． ． 平面 和平面 为同一个平面，∴二面角 的余弦值为 ； 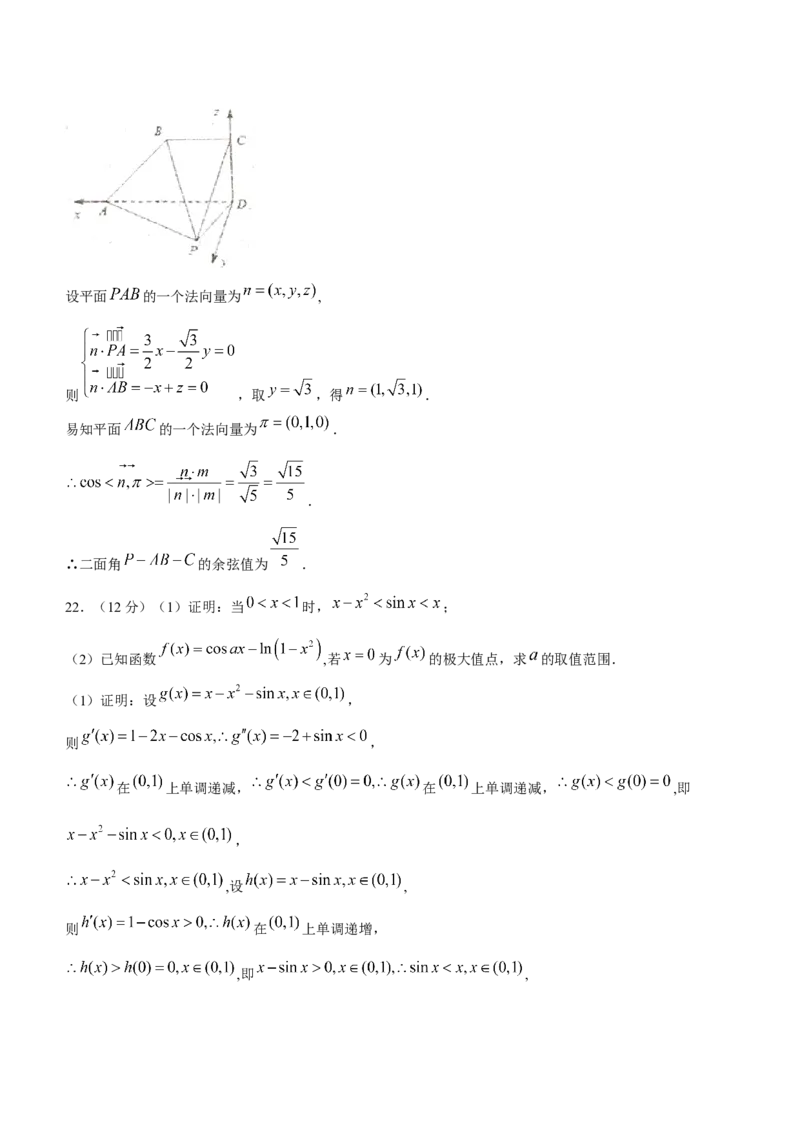方法二、以 为坐标原点， 所在直线分别为 轴和 轴，建立如图所示的空间直角坐标系， 不妨设 ,则 ， ， ，设平面 的一个法向量为 , 则 ，取 ，得 ． 易知平面 的一个法向量为 ． ． ∴二面角 的余弦值为 ． 22．（12分）（1）证明：当 时， ； （2）已知函数 ,若 为 的极大值点，求 的取值范围． （1）证明：设 ， 则 ， 在 上单调递减， 在 上单调递减， ,即 ， ,设 , 则 在 上单调递增， ,即 ,综合可得：当 时， ； （2）解： ， 且 , ①若 ,即 时， 易知存在 ，使得 时， ， 在 上单调递增， ， 在 上单调递增，这显然与 为函数的极大值点相矛盾，故舍去； ②若 ,即 或 时， 存在 ，使得 时， ， 在 上单调递减，又 ， ∴当 时， 单调递增； 当 时， 单调递减，满足 为 的极大值点，符合题意； ③若 ,即 时， 为偶函数， ∴只考虑 的情况， 此时 时， ， 在 上单调递增，与显然与 为函数的极大值点相矛盾，故舍去， 综合可得： 的取值范围为 ．