2002年广东高考数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_广东

2002 年广东高考数学真题及答案 第Ⅰ卷(选择题 共60分)￿ 一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一 x1 项是符合题目要求的)1．不等式 ＞０的解集为￿ x3 ￿ A．｛ｘ｜ｘ＜１｝ B．｛ｘ｜ｘ＞３｝￿ C．｛ｘ｜ｘ＜１或ｘ＞３｝ ￿ D．｛ｘ｜１＜ｘ＜３｝￿ 2．若一个圆锥的轴截面是等边三角形，其面积为 3，则这个圆锥的全面积是￿ ￿Ａ．３π ￿ Ｂ．３ 3π ￿Ｃ．6π￿ Ｄ．９π 3．极坐标方程ρ２ｃｏｓ２θ＝１所表示的曲线是￿ ￿A．两条相交直线￿B．圆￿ ￿C．椭圆 ￿D．双曲线￿ 4．若定义在区间(－１，０)内的函数ｆ（ｘ）＝ｌｏｇ （ｘ＋1)满足ｆ（ｘ）＞0，则ａ ２ａ 的取值范围是￿ 1 1 1 ￿ A．（０， ） ￿Ｂ．（０， ]￿ ￿Ｃ．（ ，＋∞） Ｄ．（０，＋∞） 2 2 2 1 5．已知复数ｚ＝ 2  6i，则ａｒｇ 是 Z  5  11 A． Ｂ． Ｃ． ￿Ｄ． 3 3 6 6 6．函数ｙ＝２－ｘ＋１（ｘ＞０）的反函数是￿ 1 1 ￿A．ｙ＝ｌｏｇ ，ｘ∈（１，２）; ￿Ｂ．ｙ＝－ｌｏｇ ，ｘ∈（１， ２ ２ x1 x1 ２）￿ 1 1 ￿ Ｃ．ｙ＝ｌｏｇ ，ｘ∈（１，２）;￿ Ｄ．ｙ＝－ｌｏｇ ，ｘ∈（１， ２ ２ x1 x1 ２]  7．若０＜α＜β＜ ，ｓｉｎα＋ｃｏｓα＝ａ，ｓｉｎβ＋ｃｏｓβ＝ｂ，则 4 A．ａ＞ｂ ￿ Ｂ．ａ＜ｂ ￿Ｃ．ａｂ＜１ ￿Ｄ．ａｂ＞2 8．在正三棱柱ABC—AＢＣ中，若ＡＢ＝ 2ＢＢ，则AB与ＣＢ所成的角的大小为￿ １ １ １ １ １ １ ￿ A．60° ￿Ｂ．９０° ￿Ｃ．4５° ￿Ｄ．120° 9．设ｆ（ｘ）、ｇ（ｘ）都是单调函数，有如下四个命题￿ ①若ｆ（ｘ）单调递增，ｇ（ｘ）单调递增，则ｆ（ｘ）－ｇ（ｘ）单调递增；￿ ②若ｆ（ｘ）单调递增，ｇ（ｘ）单调递减，则ｆ（ｘ）－ｇ（ｘ）单调递增；￿ ③若ｆ（ｘ）单调递减，ｇ（ｘ）单调递增，则ｆ（ｘ）－ｇ（ｘ）单调递减；￿ ④若ｆ（ｘ）单调递减，ｇ（ｘ）单调递减，则ｆ（ｘ）－ｇ（ｘ）单调递减其中，正 确的命题是￿ ￿A． ①③ ￿Ｂ．①④ ￿Ｃ．②③ ￿Ｄ．②④￿ 10．对于抛物线ｙ２＝４ｘ上任意一点Q，点P(a,0)都满足｜ＰＱ｜≥｜ａ｜，则a的取值 第1页 | 共7页范围是￿ ￿A．（－∞,０） ￿B．（－∞,２） ￿ C．［０,２］ ￿D．（０,２）￿ 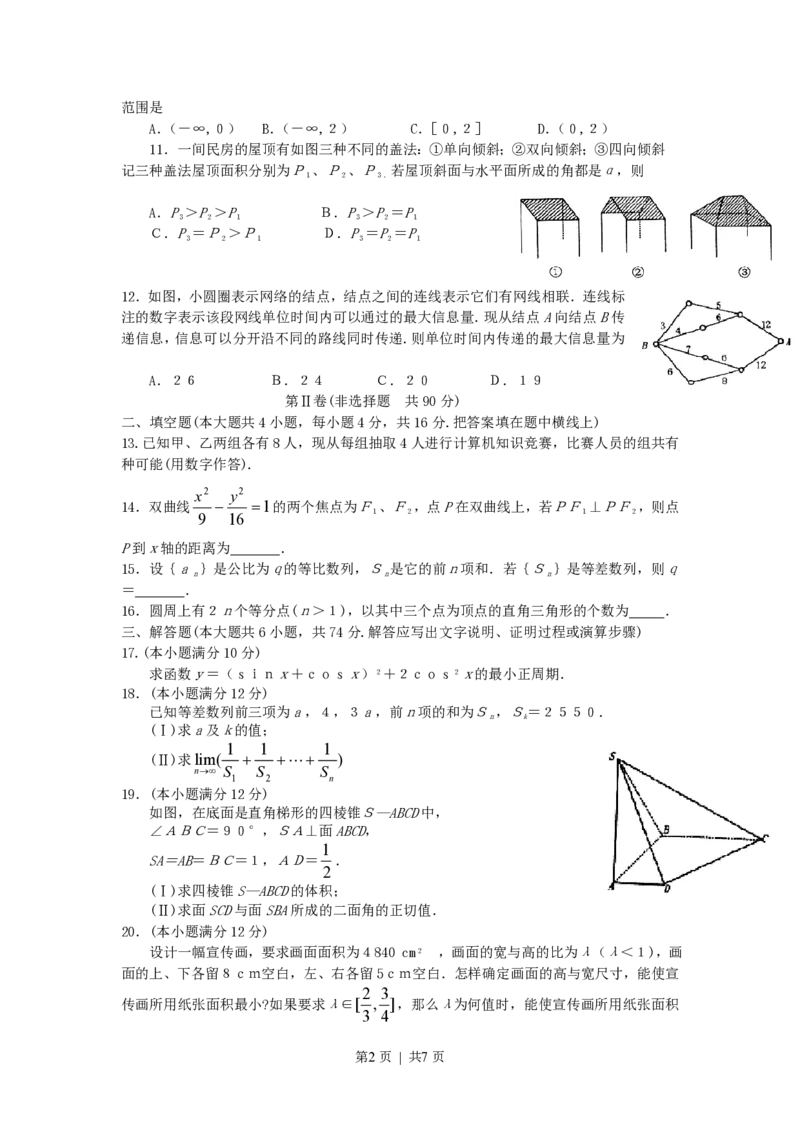11．一间民房的屋顶有如图三种不同的盖法：①单向倾斜；②双向倾斜；③四向倾斜￿ 记三种盖法屋顶面积分别为Ｐ、Ｐ、Ｐ 若屋顶斜面与水平面所成的角都是α，则￿ １ ２ ３． ￿A．P＞P＞P ￿Ｂ．P＞P＝P￿ ３ ２ １ ３ ２ １ ￿Ｃ．P＝Ｐ＞Ｐ Ｄ．P＝P＝P ３ ２ １ ３ ２ １ 12．如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相联．连线标 注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点A向结点B传 递信息，信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为 ￿ ￿A．２６￿ Ｂ．２４ ￿Ｃ．２０ ￿Ｄ．１９ ￿第Ⅱ卷(非选择题 共90分)￿ 二、填空题(本大题共4小题，每小题4分，共16分.把答案填在题中横线上)￿ 13.已知甲、乙两组各有8人，现从每组抽取4人进行计算机知识竞赛，比赛人员的组共有 种可能(用数字作答).￿ x2 y2 14．双曲线  1的两个焦点为Ｆ、Ｆ，点P在双曲线上，若ＰＦ⊥ＰＦ，则点 １ ２ １ ２ 9 16 P到ｘ轴的距离为 ．￿￿ 15．设｛ａ｝是公比为ｑ的等比数列，Ｓ是它的前ｎ项和．若｛Ｓ｝是等差数列，则ｑ ｎ ｎ ｎ ＝ ． 16．圆周上有２ｎ个等分点(ｎ＞１)，以其中三个点为顶点的直角三角形的个数为 ． 三、解答题(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)￿ 求函数ｙ＝（ｓｉｎｘ＋ｃｏｓｘ）２＋２ｃｏｓ２ｘ的最小正周期． 18．(本小题满分12分)￿ 已知等差数列前三项为ａ，４，３ａ，前ｎ项的和为Ｓ，Ｓ＝２５５０． ｎ k (Ⅰ)求ａ及ｋ的值；￿ 1 1 1 (Ⅱ)求lim(    )  n S S S 1 2 n 19．(本小题满分12分)￿ 如图，在底面是直角梯形的四棱锥Ｓ—ABCD中， ∠ＡＢＣ＝９０°，ＳＡ⊥面ABCD， 1 SA＝AB＝ＢＣ＝１，ＡＤ＝ ． 2 (Ⅰ)求四棱锥S—ABCD的体积；￿ (Ⅱ)求面SCD与面SBA所成的二面角的正切值． 20．(本小题满分12分)￿ 设计一幅宣传画，要求画面面积为４840 cm２￿，画面的宽与高的比为λ（λ＜１)，画 面的上、下各留８ｃｍ空白，左、右各留5ｃｍ空白．怎样确定画面的高与宽尺寸，能使宣 2 3 传画所用纸张面积最小?如果要求λ∈[ , ]，那么λ为何值时，能使宣传画所用纸张面积 3 4 第2页 | 共7页最小? 21．(本小题满分14分)￿ x2 已知椭圆  y2 1的右准线l与x轴相交于点E，过椭圆右焦点F的直线与椭圆相 2 交于A、B两点，点C在右准线l上，且ＢＣ∥x轴￿求证直线AC经过线段EF的中点． 22．(本小题满分14分)￿ 设ｆ（ｘ）是定义在R上的偶函数，其图象关于直线ｘ＝１对称￿对任意ｘ，ｘ∈ １ ２ 1 ［０， ］，都有ｆ（ｘ＋ｘ）＝ｆ（ｘ）·ｆ（ｘ），且f(1)=ａ＞０．￿ １ ２ １ ２ 2 1 1 (Ⅰ)求ｆ( ), f( )；￿ 2 4 (Ⅱ)证明ｆ（ｘ）是周期函数；￿ 1 （Ⅲ）记ａ＝ｆ（２ｎ＋ ），求lim(lna )． ｎ 2n n n 第3页 | 共7页参考答案 一、选择题￿1．C 2.A 3.D 4.A 5.B 6.A 7.B 8.B 9.C 10.B 11.D 12.D￿￿ 16 二、填空题￿13.4900 14. 15.1 16.2n(n-1)￿ 5 三、解答题￿ 17.解：ｙ=（ｓｉｎｘ＋ｃｏｓｘ）２＋２ｃｏｓ２ｘ￿ ＝１＋ｓｉｎ２ｘ＋２ｃｏｓ２ｘ￿ ＝ｓｉｎ２ｘ＋ｃｏｓ２ｘ＋２ ５分￿  ＝ 2sin(2x )2 8分 4 所以最小正周期Ｔ＝π． 10分￿ 18.解：(Ⅰ)设该等差数列为｛ａ｝，￿ ｎ 则a＝ａ，ａ＝４，ａ＝３ａ，Ｓ＝２５５０．￿ １ ２ ３ ｋ 由已知有a+3a=2×４，解得首项a＝ａ＝２，￿ １ 公差d=a－ａ＝２． 2分￿ ２ １ k(k 1) k(k 1) 代入公式S＝ｋ·ａ＋ d 得k2 2 2550 ｋ １ 2 2 ∴ｋ２＋ｋ－２５５０＝０￿ 解得k=50,k=-51(舍去)￿ ∴a=2,k=50. 6分￿ n(n1) (Ⅱ)由S  na  d得S＝ｎ（ｎ＋１），￿ n 1 2 ｎ 1 1 1 1 1 1 1 1 1 1 1 1        ( - )( - ) ( - )    S S S 12 23 n(n1) 1 2 2 3 n n1 1 2 n 1 1 9分￿ n1 1 1 1 1 lim(    )  lim(1 ) 1 12分￿  n S S S n n1 1 2 n 19．解：(Ⅰ)直角梯形ABCD的面积是￿ 1 10.5 3 M = (BC  AD)AB= 1 2分￿ 底面 2 2 4 1 1 3 1 ∴四棱锥S—ABCD的体积是V  SAM  1  4分 3 底面 3 4 4 (Ⅱ)延长BA、CD相交于点E，连结SE，则SE是所求二面角的棱￿ 6分￿ ∵ＡＤ∥ＢＣ，ＢＣ＝２ＡＤ￿￿ ∴ＥＡ＝ＡＢ＝ＳＡ，∴ＳＥ⊥ＳＢ￿￿ ∵ＳＡ⊥面ABCD，得面SEB⊥面EBC，EB是交线. 又ＢＣ⊥ＥＢ，∴ＢＣ⊥面SEB，故SB是SC在面SEB上的射影，∴CS⊥ＳＥ，￿ 所以∠ＢＳＣ是所求二面角的平面角￿ 10分￿ ∵ＳＢ＝ SA2  AB2  2,BC 1,BC  SB 第4页 | 共7页BC 2 ∴ｔｇ∠ＢＳＣ＝  SB 2 2 即所求二面角的正切值为 12分￿ 2 20.解：设画面高为ｘｃｍ，宽为λｘｃｍ￿，则λｘ２＝４８４０ 1分 设纸张面积为S，则有￿ Ｓ＝（ｘ＋１６）（λｘ＋１０）＝λｘ２＋（１６λ＋１０）ｘ＋１６０， 3分￿ 22 10 5 将ｘ＝ 代入上式得Ｓ＝５０００＋４４ 10(8  ) 5分￿   5 5 5 4840 当８  ,即 ( 1)时，S取得最小值，此时，高：ｘ＝ 88c   8 8  ｍ，￿ 5 宽：λｘ＝ 8855ｃｍ￿￿ 8分￿ 8 2 3 2 3 如果λ∈［ , ］，可设    ，则由S的表达式得￿ 3 4 3 1  2 4 5 5 Ｓ（ λ ） － Ｓ（ λ ） ＝ ４ ４ 10(8   8   ) = １ ２ 1 2   1 2 2 5 5 44 10(  1   2 )(8  5  ) 10分￿由于  1  2  3  8 ,故8   0 11 2 1 2 因此Ｓ（λ）－Ｓ（λ）＜０，￿ １ ２ 2 3 所以S（λ）在区间［ , ］内单调递增. 3 4 2 3 2 从而，对于λ∈［ , ］，当λ＝ 时，S（λ）取得最小值￿￿ 3 4 3 答：画面高为 88ｃｍ、宽为５５ｃｍ￿时，所用纸张面积最小；如果要求λ∈ 2 3 2 ［ , ］,当λ＝ 时，所用纸张面积最小. 12 3 4 3 分￿ 21.证明：依设，得椭圆的半焦距ｃ＝１，右焦点为F(1，0)，右准线方程为ｘ＝２， 3 点E的坐标为(2，0)，EF的中点为N( ，0)￿ 3分￿ 2 若AB垂直于x轴，则A（１，ｙ），Ｂ（１，－ｙ），Ｃ（２，－ｙ），￿￿ １ １ １ 3 ∴AC中点为N( ，0)，即AC过EF中点N.￿￿ 2 若AB不垂直于x轴，由直线AB过点F，且由BC∥x轴知点B不在x轴上，故直线AB 的方程为ｙ＝ｋ（ｘ－１），ｋ≠０．￿ 记A（ｘ ，ｙ）和Ｂ（ｘ ，ｙ ），则C（２，ｙ ）且ｘ ，ｘ 满足二次方程 １ 1 ２ ２ ２ １ ２ 第5页 | 共7页x2 k2(x1)2 1 2 即（１＋２ｋ２）ｘ２－４ｋ２ｘ＋２（ｋ２－１）＝０，￿ 4k2 2(k2 1) ∴ｘ＋ｘ＝ ,x x  １０分￿ １ ２ 12k2 1 2 12k2 3 又ｘ２ ＝２－２ｙ２ ＜２，得ｘ－ ≠０， １ １ １ 2 y 2k(x 1) y 故直线AN，CN的斜率分别为￿ｋ＝ 1  1 k  2  2k(x 1) １ 3 2x 3 2 3 2 x  1 2 1 2 2 (x 1)(x 1)(2x 3) ∴ｋ－ｋ＝２ｋ· 1 2 1 １ ２ 2x 3 1 ∵（ｘ－１）－（ｘ－１）（２ｘ－３）＝３（ｘ＋ｘ）－２ｘｘ－４￿ １ ２ １ １ ２ １ ２ 1 ＝ [12k2 4(k2 1)4(12k2)]0 12k2 ∴ｋ－ｋ＝０，即ｋ＝ｋ，故A、C、N三点共线.￿￿ １ ２ １ ２ 所以，直线AC经过线段EF的中点N. 14分￿ 1 22.(Ⅰ)解：因为对ｘ，ｘ∈［０， ］，都有ｆ（ｘ＋ｘ）＝ｆ（ｘ）·ｆ（x １ ２ １ ２ １ 2 ）, ２ 所以 x x x x 1 1 1 1 1 f(x) f(  ) f( ) f( )0,x[0,1] f(1) f(  ) f( ) f( )[f( )]2  2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 f( ) f(  ) f( ) f( )[f( )]2 2 4 4 4 4 4 ｆ（１）＝ａ＞0，￿ 3 分 1 1 1 1 ∴ f( )  a2, f( )  a4 6分 2 4 (Ⅱ)证明：依题设ｙ＝ｆ（ｘ）关于直线ｘ＝１对称，￿ 故ｆ（ｘ）＝ｆ（１＋１－ｘ），￿ 即ｆ（ｘ）＝ｆ（２－ｘ），ｘ∈R￿￿ 又由ｆ（ｘ）是偶函数知ｆ（－ｘ）＝ｆ（ｘ），ｘ∈R，￿ ∴ｆ（－ｘ）＝ｆ（２－ｘ），ｘ∈R，￿ 将上式中－ｘ以ｘ代换，得ｆ（ｘ）＝ｆ（ｘ＋２），ｘ∈Ｒ￿￿ 这表明ｆ（ｘ）是R上的周期函数，且2是它的一个周期.￿￿ 10分￿ （Ⅲ）解：由(Ⅰ)知ｆ（ｘ）≥０，ｘ∈［０，１］ 第6页 | 共7页1 1 1 1 ∵ f( )  f(n )  f[ (n1) ] 2 2n 2n 2n 1 1 1 1 1 1  f( ) f[(n1) ]  f( ) f( )  f( )[f( )]n   2n 2n 2n 2n 2n 2n 1 1 1 1 f( )  a2∴ f( )  a2n 12分￿ 2 2n 1 1 1 ∵ｆ（ｘ）的一个周期是2￿￿∴ｆ（２ｎ＋ ）=ｆ（ ）,因此a=a2n n 2n 2n 1 lim(lna )  lim( lna) 0 14分￿ n n n 2n 第7页 | 共7页