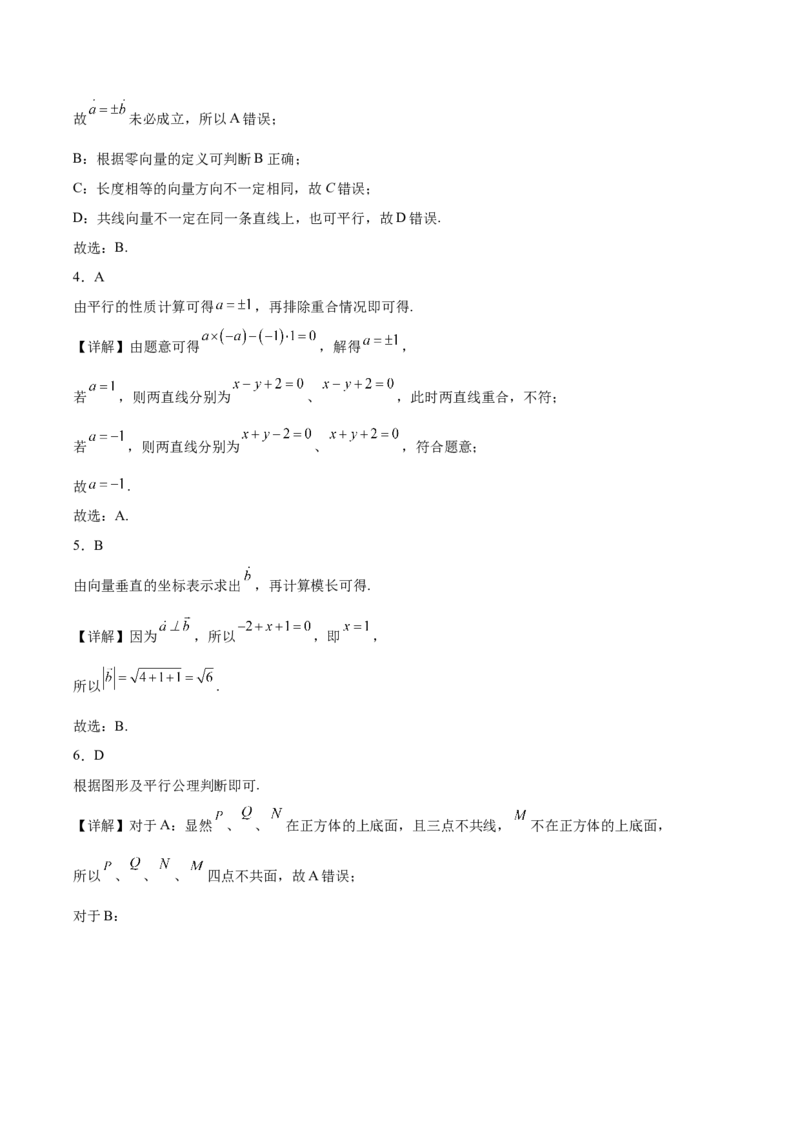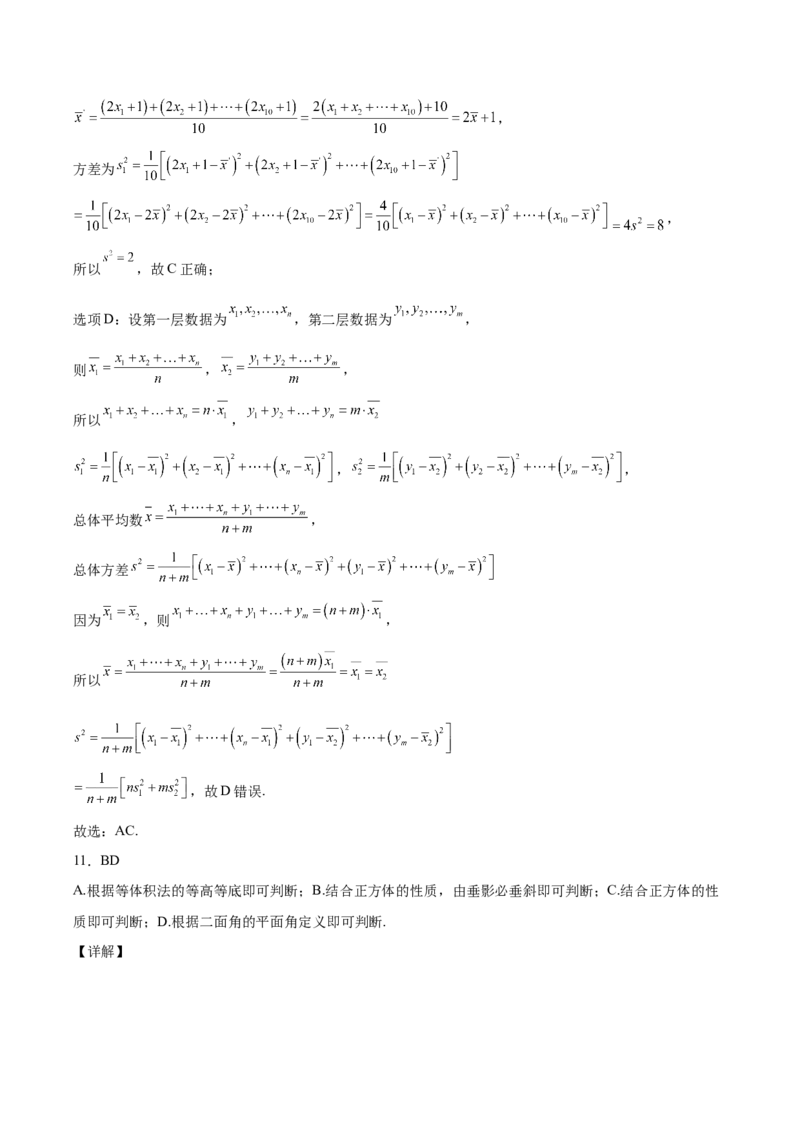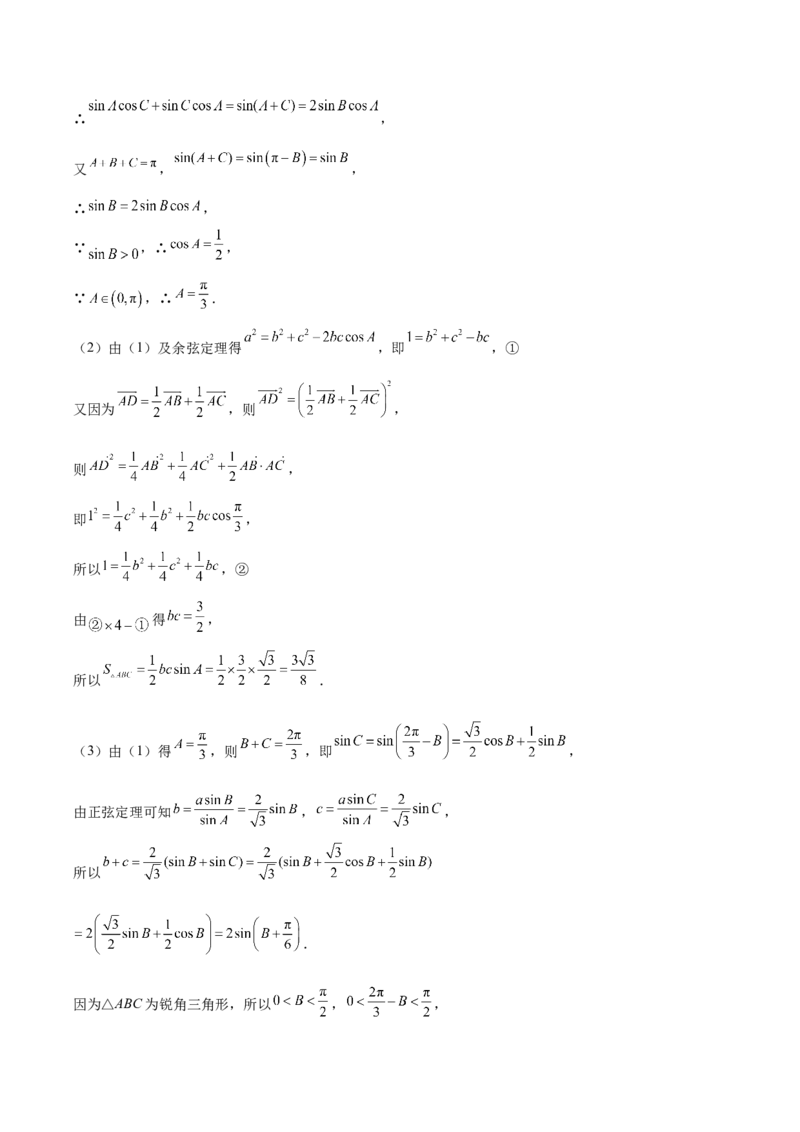文档内容
巴彦淖尔市第一中学2025-2026学年高二上学期第三次诊断性检测
数学试题
一、单选题
1.样本数据16,24,14,10,20,30,12,14,40的中位数为( )
A.14 B.16 C.18 D.20
2.已知复数 满足 ,则 的虚部为( )
A. B. C.1 D.
3.下列说法正确的是( )
A.若 ,则
B.零向量的长度是0
C.长度相等的向量叫相等向量
D.共线向量是在同一条直线上的向量
4.如果直线 与直线 平行,那么 等于( )
A. B. C.1 D.
5.已知向量 , ,且 ,那么 ( )
A.2 B. C. D.5
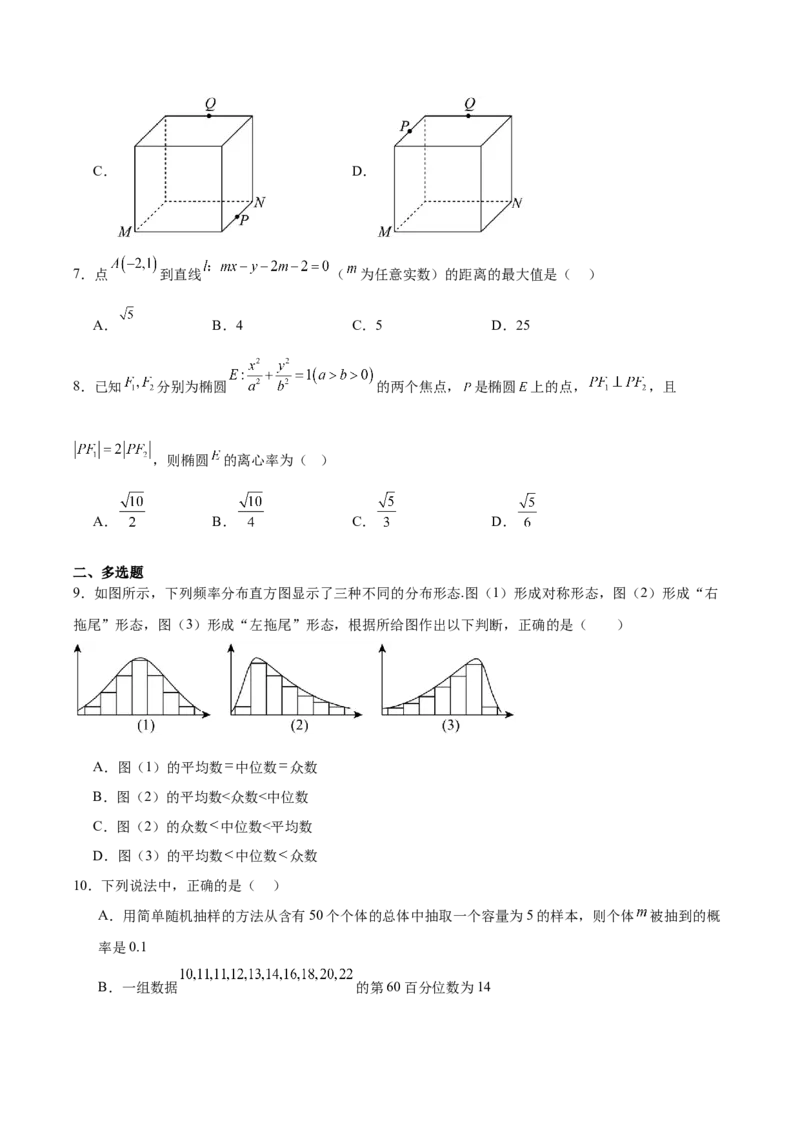
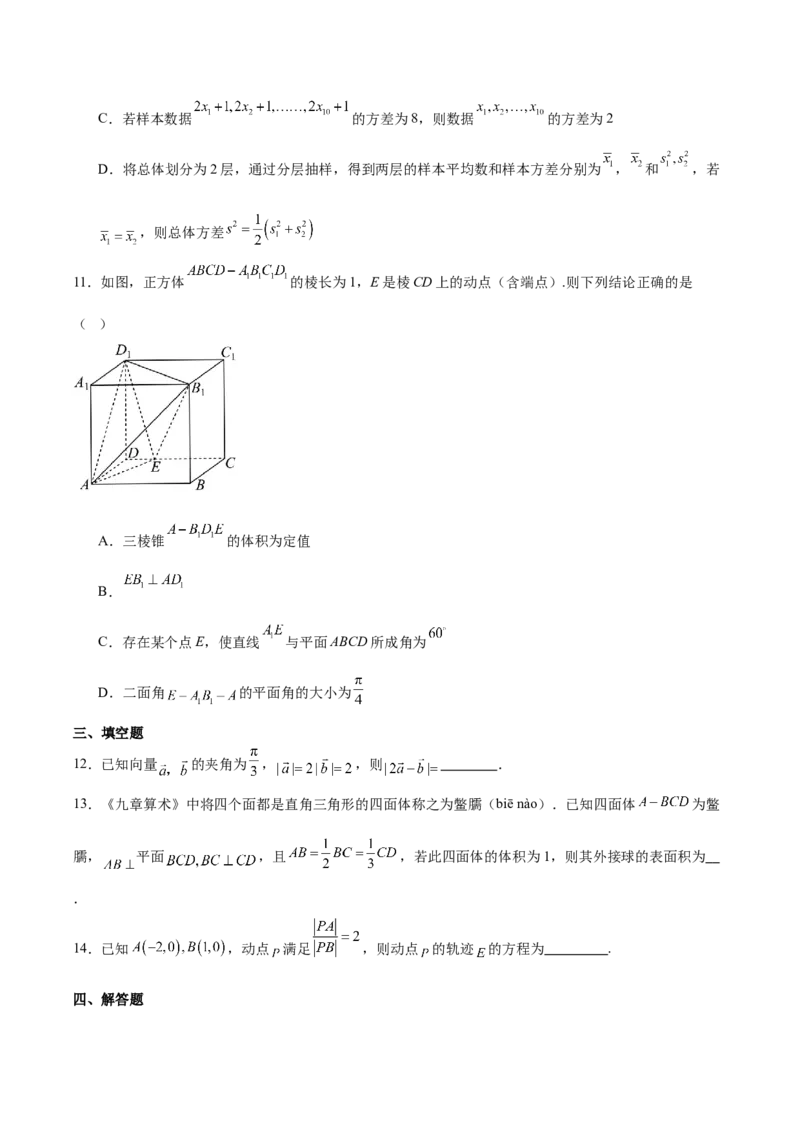
6.如图,在下列正方体中,M,N为正方体的两个顶点,P,Q分别为所在棱的中点,则在这四个正方体
中,M,N,P,Q四点共面的是( )
A. B.C. D.
7.点 到直线 ( 为任意实数)的距离的最大值是( )
A. B.4 C.5 D.25
8.已知 分别为椭圆 的两个焦点, 是椭圆 上的点, ,且
,则椭圆 的离心率为( )
A. B. C. D.
二、多选题
9.如图所示,下列频率分布直方图显示了三种不同的分布形态.图(1)形成对称形态,图(2)形成“右
拖尾”形态,图(3)形成“左拖尾”形态,根据所给图作出以下判断,正确的是( )
A.图(1)的平均数 中位数 众数
B.图(2)的平均数<众数<中位数
C.图(2)的众数 中位数<平均数
D.图(3)的平均数 中位数 众数
10.下列说法中,正确的是( )
A.用简单随机抽样的方法从含有50个个体的总体中抽取一个容量为5的样本,则个体 被抽到的概
率是0.1
B.一组数据 的第60百分位数为14C.若样本数据 的方差为8,则数据 的方差为2
D.将总体划分为2层,通过分层抽样,得到两层的样本平均数和样本方差分别为 , 和 ,若
,则总体方差
11.如图,正方体 的棱长为1,E是棱CD上的动点(含端点).则下列结论正确的是
( )
A.三棱锥 的体积为定值
B.
C.存在某个点E,使直线 与平面ABCD所成角为
D.二面角 的平面角的大小为
三、填空题
12.已知向量 的夹角为 , ,则 .
13.《九章算术》中将四个面都是直角三角形的四面体称之为鳖臑(biē nào).已知四面体 为鳖
臑, 平面 ,且 ,若此四面体的体积为1,则其外接球的表面积为
.
14.已知 ,动点 满足 ,则动点 的轨迹 的方程为 .
四、解答题15.已知椭圆 .
(1)求椭圆的长轴长,短轴长及离心率;
(2)求与椭圆 有相同的焦点,且过点 的椭圆的标准方程.
16.已知圆 ,直线 过点 .
(1)若直线 与圆 相切,求直线 的方程;
(2)若直线 与圆 交于 两点, ,求直线 的方程.
17.在 中,角A,B,C的对边分别为a,b,c,且 , .
(1)求角A;
(2)若D是线段 的中点,且 ,求 的面积;
(3)若 为锐角三角形,求 的周长的取值范围.
18.培英高中举行数学竞赛校内选拔赛(满分100分),为了了解本次竞赛成绩的情况,随机抽取了100
名参赛学生的成绩,并分成了五组:第一组 ,第二组 ,第三组 ,第四组 ,第
五组 绘制成如图所示的频率分布直方图.已知第一、二组的频率之和为0.3,第一组和第五组的频
率相同.
(1)求出频率分布直方图中 , 的值,并估计此次竞赛成绩的中位数(保留小数点后两位);
(2)现从以上各组中按比例分配的分层随机抽样方法选取20人,第二组考生成绩的平均数和方差分别为66
和37,第四组考生成绩的平均数和方差分别为84和68.5,据此估计这次第二组和第四组所有参赛学生成绩的方差;
(3)甲、乙、丙3名同学同时做试卷中同一道题,已知甲能解出该题的概率为 ,乙能解出而丙不能解出该
题的概率为 ,甲、丙都能解出该题的概率为 ,假设他们三人是否解出该题互不影响.求甲、乙、丙3
人中至少有1人解出该题的概率.
19.如图,在四棱锥 中,底面 是菱形, 且 , 平面 ,
为 的中点
(1)证明: 平面 ;
(2)求 与平面 所成的角;
(3)求点 到平面 的距离.题号 1 2 3 4 5 6 7 8 9 10
答案 B A B A B D C C ACD AC
题号 11
答案 BD
1.B
由中位数定义即可得.
【详解】将这些数据从小到大排列可得:10,12,14,14,16,20,24,30,40,
则其中位数为16.
故选:B.
2.A
利用复数除法运算化简复数 ,结合虚部定义即可求解.
【详解】由题可得 ,所以则 的虚部为 ,
故选:A
3.B
根据向量的相关概念逐一判断即可.
【详解】A: 仅表示 与 的大小相等,但是方向不确定,故 未必成立,所以A错误;
B:根据零向量的定义可判断B正确;
C:长度相等的向量方向不一定相同,故C错误;
D:共线向量不一定在同一条直线上,也可平行,故D错误.
故选:B.
4.A
由平行的性质计算可得 ,再排除重合情况即可得.
【详解】由题意可得 ,解得 ,
若 ,则两直线分别为 、 ,此时两直线重合,不符;
若 ,则两直线分别为 、 ,符合题意;
故 .
故选:A.
5.B
由向量垂直的坐标表示求出 ,再计算模长可得.
【详解】因为 ,所以 ,即 ,
所以 .
故选:B.
6.D
根据图形及平行公理判断即可.
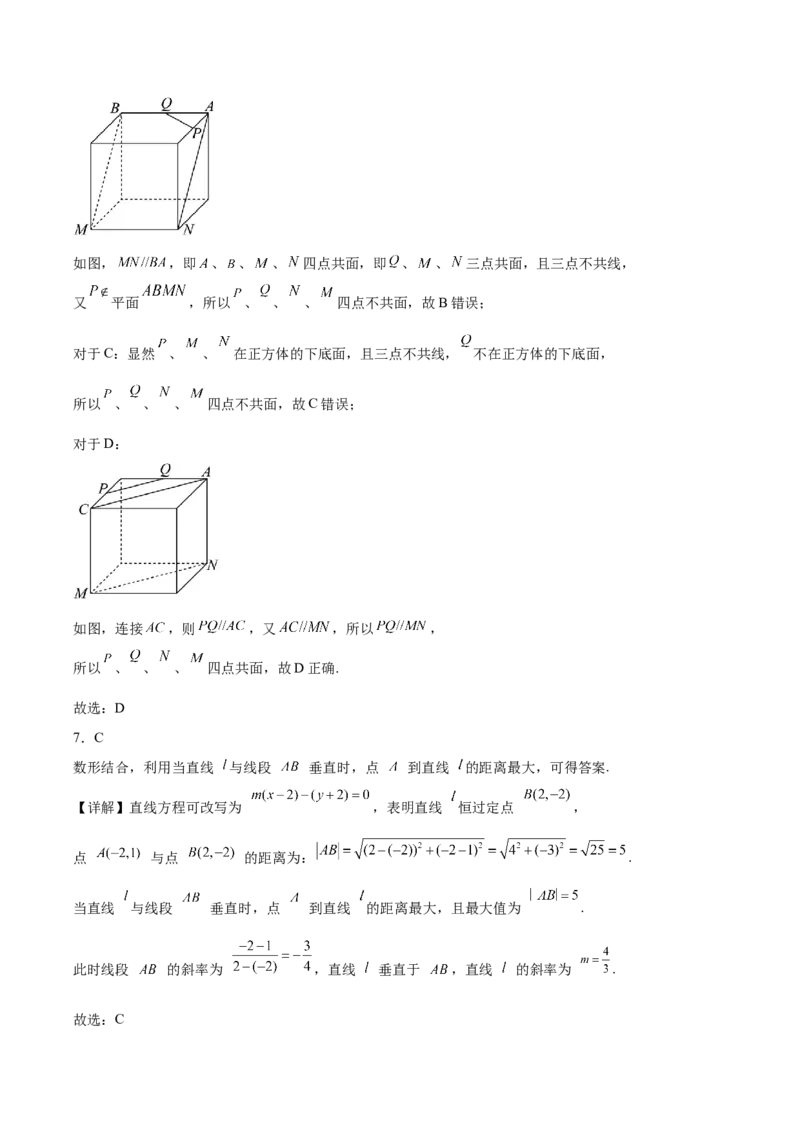
【详解】对于A:显然 、 、 在正方体的上底面,且三点不共线, 不在正方体的上底面,
所以 、 、 、 四点不共面,故A错误;
对于B:如图, ,即 、 、 、 四点共面,即 、 、 三点共面,且三点不共线,
又 平面 ,所以 、 、 、 四点不共面,故B错误;
对于C:显然 、 、 在正方体的下底面,且三点不共线, 不在正方体的下底面,
所以 、 、 、 四点不共面,故C错误;
对于D:
如图,连接 ,则 ,又 ,所以 ,
所以 、 、 、 四点共面,故D正确.
故选:D
7.C
数形结合,利用当直线 与线段 垂直时,点 到直线 的距离最大,可得答案.
【详解】直线方程可改写为 ,表明直线 恒过定点 ,
点 与点 的距离为: .
当直线 与线段 垂直时,点 到直线 的距离最大,且最大值为 .
此时线段 的斜率为 ,直线 垂直于 ,直线 的斜率为 .
故选:C8.C
利用椭圆的定义结合勾股定理,易得等式求出离心率.
【详解】由椭圆定义得: ,又因为 ,
所以解得: ,
再由于 , ,结合勾股定理可得:
,解得 ,所以椭圆 的离心率为 ,
故选:C.
9.ACD
【详解】根据平均数,中位数,众数的概念结合图形分析判断.
图(1)的分布直方图是对称的,所以平均数=中位数=众数,故A正确;
图(2)众数最小,右拖尾平均数大于中位数,故B错误,C正确;
图(3)左拖尾众数最大,平均数小于中位数,故D正确.
故选:ACD.
10.AC
由古典概型的概率可判断A,根据百分位数定义可判断B,由数据的平均数和方差的定义可判断C,D.
【详解】选项A:个体m被抽到的概率为 ,故A正确;
选项B:由于 ,第六个数为14,第七个数为16,则第60百分位数为 ,故B错误;
选项C:设数据 的平均数为 ,方差为
,
则数据 的平均数为,
方差为
,
所以 ,故C正确;
选项D:设第一层数据为 ,第二层数据为 ,
则 , ,
所以 ,
, ,
总体平均数 ,
总体方差
因为 ,则 ,
所以
,故D错误.
故选:AC.
11.BD
A.根据等体积法的等高等底即可判断;B.结合正方体的性质,由垂影必垂斜即可判断;C.结合正方体的性
质即可判断;D.根据二面角的平面角定义即可判断.
【详解】对于选项A:三棱锥 的底面积为定值,高变化,体积不为定值,故选项A不正确;
对于选项B: 两点在平面 上的射影分别为 ,即直线 在平面 上的射影为 ,
而 ,根据三垂线定理可得 .故选项B正确;
对于选项C:因为 平面 ,直线 与平面ABCD所成角为 ,
当点 和点 重合时, 在平面 射影最小,
这时直线 与平面ABCD所成角 最大值为 ,故选项C不正确;
对于选项D:二面角 即二面角 ,
因为 , , 平面 , 平面 ,
所以 即为二面角 的平面角,
在正方形 中, ,所以二面角 的大小为 ,故选项D正确.
故选:BD.
12.
根据平面向量数量积公式求出答案.
【详解】因为 ,所以 ,
.
故答案为:13.
由已知,可根据题意,设 ,然后根据体积为1,求解出 ,然后
把鳖臑的外接球可还原在以 为长宽高的长方体中,可根据长方体的外接球半径是其体对角线的
一半求解出外接球半径,从而求解外接球表面积.
【详解】由已知,因为 平面 ,可令 ,
所以 ,所以 ,
所以 ,
由已知,鳖臑的外接球可还原在以 为长宽高的长方体中,设其外接球半径为 ,
所以其外接球的半径 ,
所以其外接球的表面积 .
故答案为: .
14.
设动点 ,根据两点间距离公式,列方程即可求解.
【详解】设动点 ,则 ,
即 ,整理得 ,
故动点 的轨迹 的方程为 .
故答案为: .
15.(1)长轴长 ,短轴长 ,离心率(2)
(1)根据已知条件求得 ,从而求得长轴长,短轴长及离心率;
(2)先求得焦点坐标,然后设出所求椭圆的方程,通过代入点 来求得正确答案.
【详解】(1)由题可知 ,
所以椭圆的长轴长为 ,短轴长为 ,离心率为 .
(2)因为椭圆 的焦点为 ,
所以与其有相同的焦点的椭圆的方程可设为 ,
其中 ,
所以椭圆的方程为 ,
将 代入得 ,
解得 ,或 (舍),
所以椭圆的标准方程为 .
16.(1) 或
(2) 或
(1)考虑直线的斜率是否存在,结合直线和圆相切时的性质求解,即得答案;
(2)设直线 的方程,利用直线和圆相交时的弦长公式,即可求得答案.
【详解】(1)若直线 的斜率不存在,则直线 的方程为 ,
此时圆心 到直线 的距离为2,所以直线 与圆 相切,符合题意;当直线 的斜率存在时,设直线 的方程为 ,即 ,
因为直线 与圆 相切,所以圆心 到直线 的距离等于半径,即 ,
解得 .
所以直线 的方程为 ,即 .
综上所述,直线 的方程为 或 .
(2)由题意知直线 的斜率存在,设直线 的方程为 ,即 ,
圆心 到直线 的距离 .
所以 ,
解得 ,或 .
所以直线 的方程为 或 ,即 或 .
17.(1)
(2)
(3)
(1)先应用正弦定理化边为角,再应用两角和的正弦公式计算化简得出角A;
(2)先根据向量关系 ,左右两边平方后结合余弦定理得出 ,进而得出面积即可;
(3)应用正弦定理边角转化应用辅助角公式化简,再根据角的范围应用正弦函数的性质求解.
【详解】(1)由正弦定理可知 ,
∴ ,∴ ,
又 , ,
∴ ,
∵ ,∴ ,
∵ ,∴ .
(2)由(1)及余弦定理得 ,即 ,①
又因为 ,则 ,
则 ,
即 ,
所以 ,②
由 得 ,
所以 .
(3)由(1)得 ,则 ,即 ,
由正弦定理可知 , ,
所以
.
因为△ABC为锐角三角形,所以 , ,即 , ,
则 ,即 ,
则 ,
故△ABC的周长的取值范围为 .
18.(1) ,
(2)
(3)
【详解】(1)由题意可知 ,解得 ,
可知每组的频率依次为0.05,0.25,0.45,0.2,0.05,
设中位数为 ,因为 ,
所以 ,所以 ,解得 ,
故此次竞赛成绩的中位数约为 分.
(2)设第二组、第四组的平均数与方差分别为 ,
且两组频率之比为 ,成绩在第二组、第四组的平均数 ,
成绩在第二组、第四组的方差
,
故估计这次第二组和第四组所有参赛学生成绩的方差是 .
(3)设“甲解出该题”为事件A,“乙解出该题”为事件B,“丙解出该题”为事件 ,
“甲、乙、丙3人中至少有1人解出该题”为事件 ,
由题意得 ,所以 ,
所以 ,所以乙、丙分别解出该题的概率为 ,
则 ,因为 ,
所以 ,因为 相互独立,
所以 ,
所以甲、乙、丙3人中至少有1人解出该题的概率为 .
19.(1)证明见解析;
(2) ;
(3) .
【详解】(1)连接BD交AC于O,连接OE.易得O为BD中点,又 为 的中点,
则 ,又 平面 , 平面 ,则 平面 ;
(2)如图作 ,因 平面 , 平面 ,
则 ,又 平面 , ,则 平面 .
连接 ,则 为 与平面 所成的角.
由题可得 , , ,则 .
(3)如图,取CD中点为 ,连接AH,易得 .
则以A为原点,AB所在直线为x轴,AP所在直线为z轴,AH所在直线为y轴建立空间直角坐标系.则
.
, .设平面 法向量为 ,则 .
令 ,则 ,故取 .
则点 到平面 的距离为 .