文档内容
2023-2024 学年度第一学期期中检测试题
高 三 数 学
2023.11.15
(全卷满分150分,考试时间120分钟)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项符合要求)
1.已知集合M={x|0≤log x≤1},B={x||x-3|≤1},则A∩B=( ).
3
A.[1,2] B.[1,4] C.[2,3] D.[2,4]
2.“α=0”是“sinα=0”的( ).
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
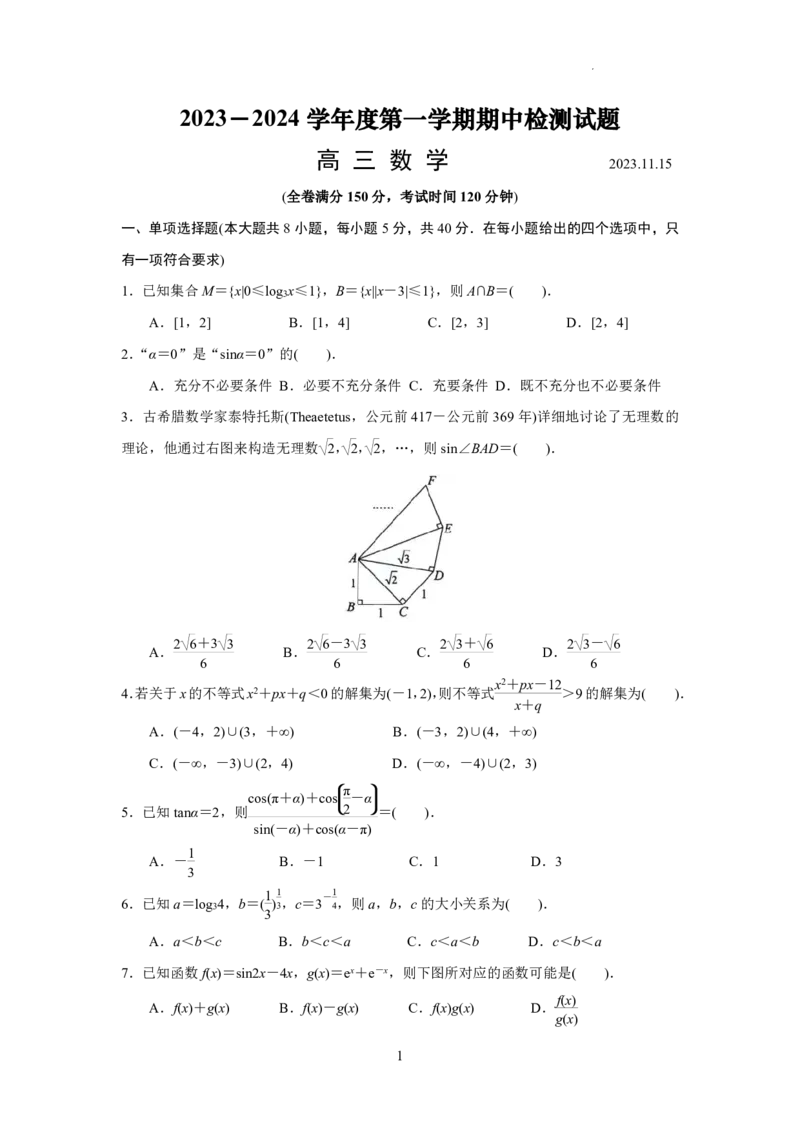
3.古希腊数学家泰特托斯(Theaetetus,公元前417-公元前369年)详细地讨论了无理数的
理论,他通过右图来构造无理数 2,2,2,…,则sin∠BAD=( ).
2 6+3 3 2 6-3 3 2 3+ 6 2 3- 6
A. B. C. D.
6 6 6 6
x2+px-12
4.若关于x的不等式x2+px+q<0的解集为(-1,2),则不等式 >9的解集为( ).
x+q
A.(-4,2)∪(3,+∞) B.(-3,2)∪(4,+∞)
C.(-∞,-3)∪(2,4) D.(-∞,-4)∪(2,3)
π
cos(π+α)+cos -α
5.已知tanα=2,则 2 =( ).
sin(-α)+cos(α-π)
1
A.- B.-1 C.1 D.3
3
6.已知a=log 3 4,b=(
1
)
1
3 ,c=3
-1
4 ,则a,b,c的大小关系为( ).
3
A.a<b<c B.b<c<a C.c<a<b D.c<b<a
7.已知函数f(x)=sin2x-4x,g(x)=ex+e-x,则下图所对应的函数可能是( ).
f(x)
A.f(x)+g(x) B.f(x)-g(x) C.f(x)g(x) D.
g(x)
1
学科网(北京)股份有限公司π 1
8.有两个点在y轴上移动,t时刻的位置分别由函数y =(t- )sint和y = -cost确定,在(0,
1 2
3 2
2π)时段内两点重合的时刻t有( ).
A.1个 B.2个 C.3个 D. 4个
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项
符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分)
9.下列函数中,最小值是4的有( ).
4 4 4 4
A.y=2x+ B.y=lnx+ C.y=|sinx|+ D.y=x2+
2x lnx |sinx| x2
10.下列选项中,能说明“ x∈(-∞,2),都有x2<4”为假命题的x取值有( ).
A.-4 B.∀-2 C.0 D.3
π
11.在△ABC中,角A、B、C所对的边分别为a、b、C,则能推出A= 的有( ).
3
A.asinC- 3ccosA=0 B. 3bsinA-acosC=(c-b)cosA
3c
C.tan(A+B)(1-tanAtanB)= D. 3bsinA-acosC=(c+b)cosA
acosB
12.已知函数f(x)及其导函数f′(x)的定义域均为R,且满足f(x)=-f(6-x),f′(x)=2-f′(4-
x),f′(3)=-1,记g(x)=2f(3-x)-1,则下列说法中正确的有( ).
A.函数f′(x)的图象关于(5,1)对称 B.函数y=f′(2x+4)-1为奇函数
C.函数g′(x)的图象关于x=1对称 D.数列{g′(n)}的前2023项之和为-4050
三、填空题(本大题共4小题,每小题5分,共20分)
13.已知函数f(x)=xα的图象过点(2,8),则f′(1)= ▲ .
1
14.将函数y=sinx图象上每一个点的横坐标变为原来的 倍(纵坐标不变),然后再向右平移
2
π
个单位长度,得到函数y=f(x)的图象,则函数f(x)的解析式为 ▲ .
6
1 3
15.已知正数a,b满足a+3b=4,则 + 的最小值为 ▲ .
a+1 b+1
16.若函数f(x)=x3+bx2+cx+d(b,c,d∈R)恰有两个零点x ,x ,且|x -x |=1,则函数
1 2 2 1
f(x)所有可能的极大值为 ▲ .
四、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤)
2
学科网(北京)股份有限公司17.(本小题满分10分)
π
已知函数f(x)=4sin(ωx+φ)(ω>0,|φ|< )的图象过点(0,2 3)、(x ,0)、(x ,0),且|x
1 2 1
2
π
-x |的最小值为 .
2
2
(1)求函数f(x)的解析式,并求出该函数的单调递增区间;
12 π π
(2)若f(α)= ,α∈( , ),求sin2α的值.
5 12 2
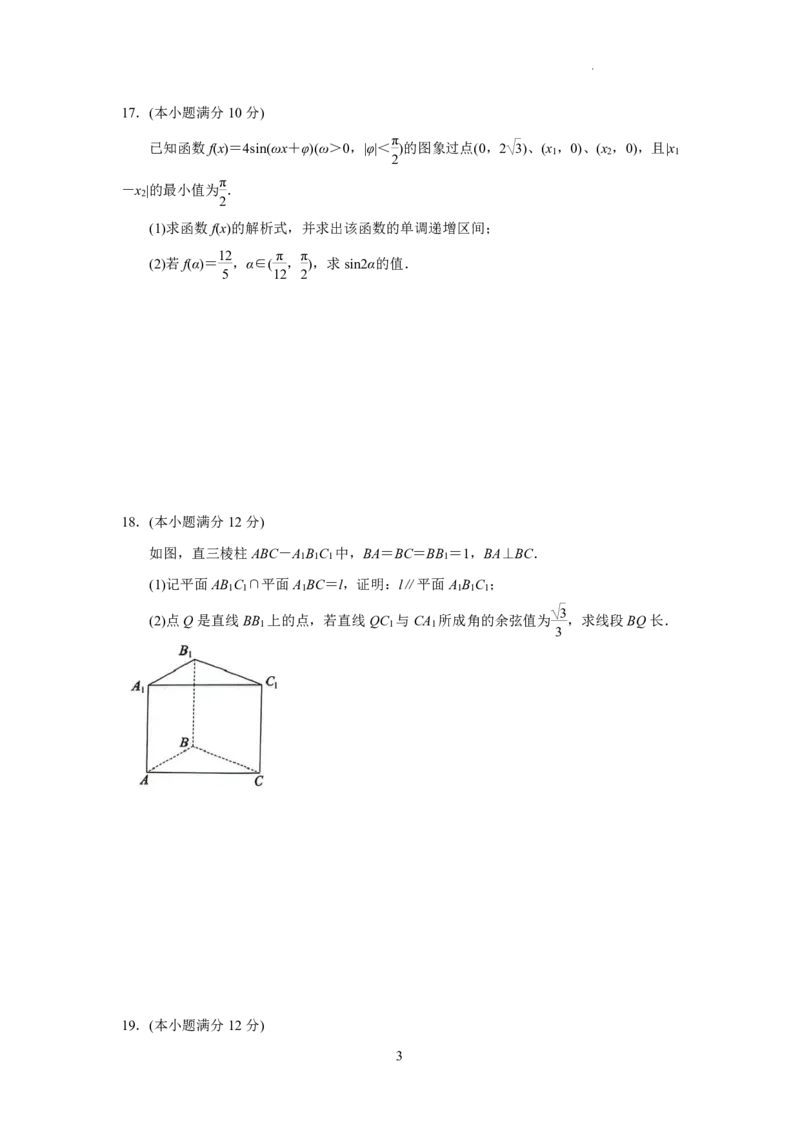
18.(本小题满分12分)
如图,直三棱柱ABC-A B C 中,BA=BC=BB =1,BA⊥BC.
1 1 1 1
(1)记平面AB C ∩平面A BC=l,证明:l∥平面A B C ;
1 1 1 1 1 1
3
(2)点Q是直线BB 上的点,若直线QC 与CA 所成角的余弦值为 ,求线段BQ长.
1 1 1
3
19.(本小题满分12分)
3
学科网(北京)股份有限公司-2x+a
定义域为R的函数f(x)= 是奇函数.
2x+1+2
(1)求实数a的值;
π
(2)若存在θ∈[- ,0],使得f( 3sinθcosθ)+f(k-cos2θ)>0成立,求实数k的取值范围.
4
20.(本小题满分12分)
某品牌方便面每袋中都随机装入一张卡片(卡片有A、B、C二种),规定:如果集齐A、
B、C卡片各一张,便可获得一份奖品.
(1)已知该品牌方便面有两种口味,为了了解这两种口味方便面中C卡片所占比例情况,
小明收集了以下调查数据:
口味1 口味2 合计
C卡片 20 10 30
非C卡片 75 45 120
合计 95 55 150
根据以上数据,判断是否有99%的把握认为“该品牌方便面中C卡片所占比例与方便面口
味有关”?
(2)根据《中华人民共和国反不正当竞争法》,经营者举办有奖销售,应当向购买者明示
奖品种类、中奖概率、奖品金额或者奖品种类、兑奖时间和方式.经小明查询,该方便面中
2 2 1
A卡片、B卡片和C卡片的比例分别为 ,,,若小明一次购买3袋该方便面.
5 5 5
①求小明中奖的概率;
②若小明未中奖,求小明未获得C卡的概率.
n(ad-bc)2
附:χ2= ,
(a+b)(c+d)(a+c)(b+d)
4
学科网(北京)股份有限公司P(χ2≥x ) 0.050 0.010 0.001
0
x 3.841 6.635 10.828
0
21.(本小题满分12分)
在△ABC中,AC= 3AB,且BC边上的中线AD长为1.
(1)若BC=2AB,求△ABC的面积;
(2)若∠ABC=2∠DAC,求BC的长.
22.(本小题满分12分)
已知函数f(x)=x2-px-qlnx(p,q∈R)
(1)若p=a,q=a2,f(x)的最小值为0,求非零实数a的值;
(2)若p=a2,q=a,f(x)≥0恒成立,求实数a的取值范围.
5
学科网(北京)股份有限公司