文档内容
2024——2025学年惠来一中高二第一学期第一次阶段考试
数 学 试 题
满分150分,时间120分钟
一、单项选择题:本题共8小题,每小题5分,共40分.在每个小题绐岀的四个选项中,
只有一项是符合题目要求的.
1.已知集合 ,集合 ,则 ( )
A. B. C. D.
2.复数z满足 ,则 ( )
A.1 B.2 C. D.4
3.设 的平均数为 与 的平均数为 与 的平均数为 .若 ,则 与 的大
小关系是( )
A. B. C. D.不能确定
4.已知某圆锥的侧面积为 ,轴截面面积为1,则该圆锥的母线与底面所成的角为( )
A. B. C. D.
5.小刚参与一种答题游戏,需要解答A,B,C三道题.已知他答对这三道题的概率分别为 , , ,
且各题答对与否互不影响,若他恰好能答对两道题的概率为 ,则他三道题都答错的概率为( )
A. B. C. D.
6.已知 , ,且 恒成立,则 的取值范围为( )
A. B. C. D.
7.如图,边长为2的正方形 沿对角线 折叠,使 ,则三棱锥 的体积为
( )A. B. C. D.4
8. 是定义在R上的函数,若 ,且对任意 ,满足 ,
,则 ( )
A.2023 B.2024 C.2025 D.2026
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多
顶符合题目要求。全部选对的得6分,有选错的得0分,若只有2个正确选顶,每选对
一个得3分;若只有3个正确选项,每选对一个得2分。
9.已知向量 , , ,则下列结论正确的是( )
A.向量 与向量 的夹角为 B.
C.向量 在向量 上的投影向量为 D.向量 与向量 , 共面
10.把函数 的图象向右平移 个单位长度,得到的函数是
一个奇函数,则下列说法正确的是( )
A. 的最小正周期为 B.
C.当 时, 的值域为
D.若方程 在区间 上恰有六个不等实根,则实数m的取值范围为11.如图,点 是棱长为2的正方体 的表面上一个动点,则( )
A.当 在平面 上运动时,四棱锥 的体积不变
B.当 在线段 上运动时, 与 所成角的取值范围是
C.若 是 的中点,当 在底面 上运动,且满足 平面
时, 长度的最小值是
D.使直线 与平面 所成的角为 的点P的轨迹长度为
三、填空题:本题共3小题,每小题5分,共计15分.
12.电影《孤注一掷》的上映引发了电信诈骗问题热议,也加大了各个社区反电信诈骗的宣传力度.
已知某社区共有居民480人,其中老年人200人,中年人200人,青少年80人,若按年龄进行等比
例的分层随机抽样,共抽取36人作为代表,则中年人比青少年多 人
13.邢台一中高二年级研究性学习小组为了实地测量某塔的高度,选取与
塔底中心O在同一个水平面内的两个测量基点A与B,在A点测得:塔顶P
的仰角为45°,O在A的北偏东60°处,B在A的正东方向36米处,且在B
点测得O与A的张角为45°,则此塔的高度约为 米(四舍五入,
保留整数.参考数据: , ).
14.已知函数 若关于x的方程 有4个解,分别为 , , ,
,其中 ,则 , 的取值范围是 .
四、解答题:本题共5小题,共计77分.解答时应写出文字说明、证明过程或演算步骤.
15.已知空间中三点 ,设(1)已知 ,求 的值;
(2)若 ,且 ,求 的坐标.
16.已知 的内角 所对的边分别是 .
(1)求角 ;
(2)若 外接圆的面积为 ,且 为锐角三角形,求 周长的取值范围.
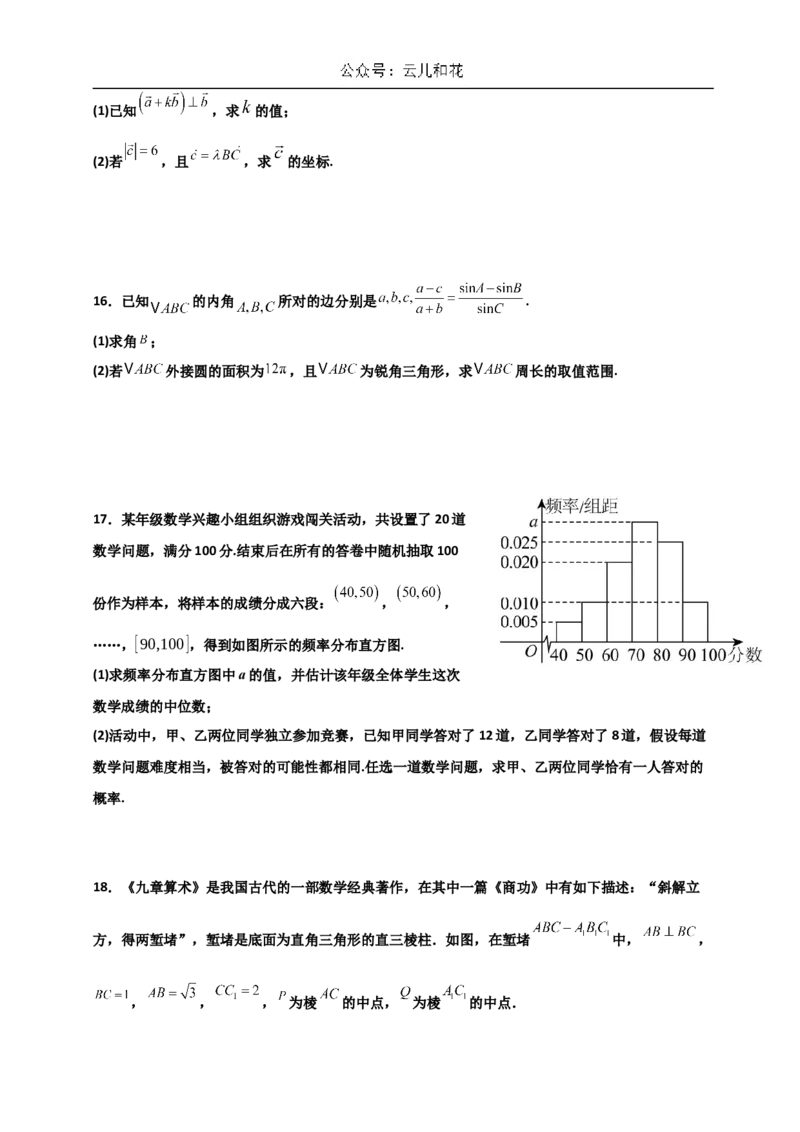
17.某年级数学兴趣小组组织游戏闯关活动,共设置了20道
数学问题,满分100分.结束后在所有的答卷中随机抽取100
份作为样本,将样本的成绩分成六段: , ,
……,[90,100],得到如图所示的频率分布直方图.
(1)求频率分布直方图中a的值,并估计该年级全体学生这次
数学成绩的中位数;
(2)活动中,甲、乙两位同学独立参加竞赛,已知甲同学答对了12道,乙同学答对了8道,假设每道
数学问题难度相当,被答对的可能性都相同.任选一道数学问题,求甲、乙两位同学恰有一人答对的
概率.
18.《九章算术》是我国古代的一部数学经典著作,在其中一篇《商功》中有如下描述:“斜解立
方,得两堑堵”,堑堵是底面为直角三角形的直三棱柱.如图,在堑堵 中, ,
, , , 为棱 的中点, 为棱 的中点.(1)证明:平面 平面 ;
(2)求二面角 的正切值;
(3)求 与平面 所成角的正弦值.
19.已知 是指数函数,且过点 是定义域为 的奇函数
(1)求 的值;
(2)若存在 ,使不等式 成立,求实数 的取值范围;
(3)若函数 恰有2个零点,求实数 的取值范围